中职生几何思维中符号信息和表象信息之间联系的研究
孔秀岩
摘 要: 本文通过调查与访谈的方法对中职生几何思维中模式加工机制进行了研究,得出了一些重要结论,可以为中职院校几何教育改革提供参考意见,同时,在中国中职几何教育的背景下,正面解决了Presmeg提出的教师应如何帮助学生建立符号信息和表象信息之间的联系的问题。
关键词: 几何思维 符号信息 表象信息 模式加工机制
1.引言
1.1研究问题
主要研究以下三个问题:(1)中职生符号信息和表象信息之间联系的现状;(2)中职生将符号信息转换为表象信息的模式加工机制;(3)有效的几何教与学的策略是什么?
1.2研究意义
在中职几何教育的背景下,笔者正面解决了Presmeg提出的问题:教师应如何帮助学生建立符号信息和表象信息之间的联系[1]?这一问题的解决,不仅丰富了符号信息和表象信息两者交叉领域的研究内容,还为未来该交叉领域的国际比较研究奠定了基础。可以为中职院校几何教育改革提供客观的建议:在制定几何课程标准时,应如何确定适合学生特点的课程目标。
2.文献探讨
2.1符号信息
符号是某种事物的记号,人们总是探索用简单的记号表现复杂的事物,于是产生各种记号。符号一词现在用得非常广泛,无处不在,可以说我们生活在符号的世界中。符号是人类沟通思想、传达信息的视觉语言,优秀的符号在传播过程中有事半功倍的作用。随着人类认识的发展,符号的概念已不再限于人类语言活动的一些标志,它已经扩展到人文科学、神话、宗教、文学等多方面。数学符号是人类集体智慧的结晶,不仅方便了数学研究和数学知识的传播,而且把人类语言学推上新的高度。数学家的一大贡献是他们关于数学符号的创造性劳动,被认为是对人类语言学的丰富和发展。
2.2表象信息
早在古希腊时期表象就已被认为是很有价值的。不同时期的研究者对表象有着不同的认识和定义方式,如何给表象下一个清晰的定义和明确的界定,在目前的认知心理学的研究中仍然是激烈争论的问题,比较有代表性的有顾泠沅等人认为,所谓表象,就是信息在头脑中的形象性表征方式[2],是现实原型在思维过程中的再现。笔者比较认同赵为华的定义方式:表象是指人们感知过的某一事物,其形象常常会在头脑中以痕迹的形式保留下来,以后这种事物虽未出现,但在一定条件(刺激)影响下,作为在没有直接信息作用(知觉)时对内在长时记忆中信息加工、提取和重组的一种信息表征的方式[3]。在数学教学中,数学表象在培养学生数学思维、发现问题和解决问题的能力、培养学生的数学联想和想象等方面都发挥重要的作用。在中职数学学习阶段,大多数数学信息都能产生数学表象,这也是在中职数学教学中研究数学表象的意义所在。
3.研究方法
笔者选取苏南某地区办学条件较好的一个学校作为研究样本,在选取班级的时候,我们选取的都是数学成绩在级部为中等的班级。所谓中等,主要是从班级学生入学时的平均分鉴定的。本研究主要通过问卷调查和访谈收集数据。
4.结论与建议
本文略去了对数据进行定性和定量分析的详细过程,我们得出以下结论。
4.1对于简单运用基本概念的容易题,大部分学生建立符号信息和表象信息之间的有效联系,且倾向于在已有认知结构中寻找简单的数学知识作为解题方法;但仍有部分学生在将符号信息转换为表象信息的过程中出现错误理解,甚至无法建立两者之间的任何联系。
4.2对于中等题,大部分学生在将符号信息转化为表象信息的过程中出现困难,原因是学生的数学认知基础没有对新知识,如向量的运算法则,进行有效的同化和顺应;同时,对于即使在两者之间建立有效联系的学生,也以运用结构简单图形而产生的数学方法为主。
4.3对于复杂题,只有极个别学生在推理过程中可以有效建立表象信息和符号信息之间的联系;受题目结构和内容复杂程度的影响,大部分学生放弃了对符号信息进行思维表征和转化,从而使解题过程以空白形式呈现。
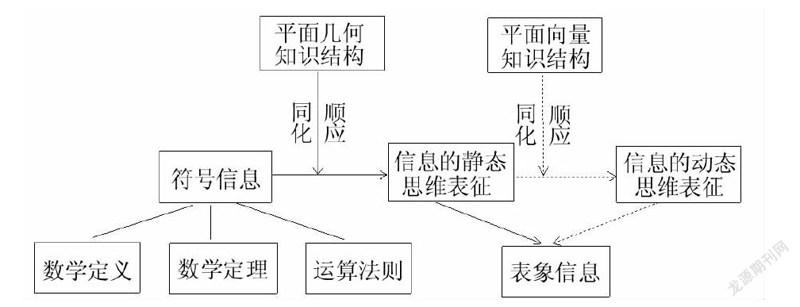
4.4基于对访谈结果的定性分析,可以得到中职生将符号信息转化为表象信息的模式加工机制,如下图所示。其中当符号信息以数学定义、定理或运算法则的形式进入学生的思维中时,大部分学生倾向于使用结合强度较大的初中平面几何知识结构对其进行同化或顺应,进而使其成为数学知识网络中的牢固子结构。这部分以初中平面几何方式表征的符号信息在学生认知结构中具有稳定性,我们称之为信息的静态思维表征,并且构成表象信息。进一步地,还有一部分学生考虑平面向量几何知识结构和初中平面几何知识结构的区别与联系,并且运用平面向量几何知识结构对信息的静态思维表征的数学知识进行再次同化和顺应。但由于平面向量几何知识结构与学生原有数学认知基础的结合强度较弱,再次同化和顺应后形成的新结构具有不稳定性。这种结构在学生思维表征中主要以动态方式呈现。当学生以动态思维方式表征数学知识时,其与信息的静态思维表征的数学知识共同形成表象信息。
5.结语
中职课堂教学模式应以学生自主探索、师生共同研究,即自探共研,为主要特征。“自探共研”课堂教学模式的核心思想是在学生的自主探索、共同研究活动中,发展学生以创新精神和实践能力为核心的素质。在中职阶段,数学课堂教学内容较多,数学思维的复杂性较大,且由于专业技能学科及顶岗实习的影响,教师强化训练学生数学思维的时间有限。因此,“自探共研”课堂教学的关键是为学生创造充分的活动机会,让学生主动地建构和发展数学知识,进而深入地理解和更多地获取数学知识。
参考文献:
[1]Presmeg,N.C.Research on visualization in learning and teaching mathematics:Emergence from psychology.In A.Gutierrez & P.Boero(Eds.),Handbook of research on the psychology of mathematics education.Rotterdam:Sense Publishers,2006.
[2]顾泠沅,鲍建生,周超.数学学习的心理基础与过程[M].上海:上海教育出版社,2009.
[3]赵为华.表象表征的若干问题.北京师范大学学报(社会科学版),1994,1.

