用类比探究新问题

姚正杰

在七年级下册《平面图形的认识（二）》有这样一道题：

（1）如图1，在△ABC中，∠ABC，∠ACB的角平分线相交于点O，∠A=40°，求∠BOC的度数；

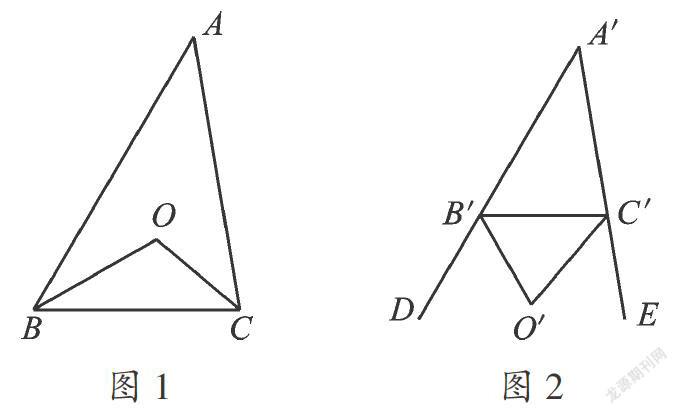
（2）如图2，△A'B'C'的两个外角（∠C'B'D，∠B'C'E）的角平分线相交于点O，∠A'=40°，求∠B'O'C'度数；

（3）由（1） （2），可以发现∠BOC与∠B'O'C'有怎样的关系？设∠A=A'=n°，∠BOC与∠B'O'C'之间是否还具有扎样的关系？为什么？

课本让我们探究的实际上是三角形2条内角（或者外角）平分线的夹角与三角形第三个角的关系.相信大家对这个问题一定不会陌生.但是，三角形中的特殊线段，除了角平分线外、还有高和中线，由此，产生了下面的一种联想：三角形的两条边上的高（或高的延长线）的夹角与三角形第三边所对的角有什么关系呢？

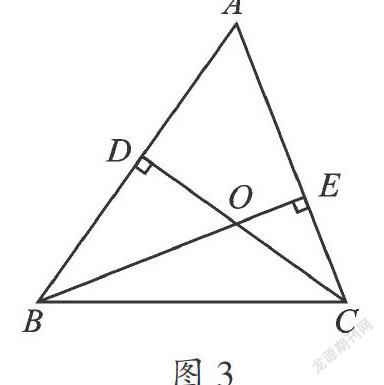
大家看下面这个问题：如图3，在△ABC中，CD⊥AB，BE⊥AC，求高CD与BE的夹角∠BOC与∠A的关系.

由CD⊥AB，BE⊥AC得∠ADO=∠AEO=90°，再由四边形内角和等于360°，可得∠A+∠DOE=180°，不难发现∠DOE与∠BOC是对顶角，所以∠DOE =∠BOC，最后可知∠A=180°-∠BOC.

接着考虑三角形的高有一个特殊性，我们都学过，钝角三角的高有2条在三角形外部，1条在内部；直角三角形有2条高就是直角边，1条是斜边上的高，所以需要对下面的情形继续进行探索.

在钝角三角形中

①钝角△ABC的两条外部的高的延长线的夹角.如图4，在△ABC中，BF⊥AC，CE⊥AB，求∠P与∠BAC的关系.

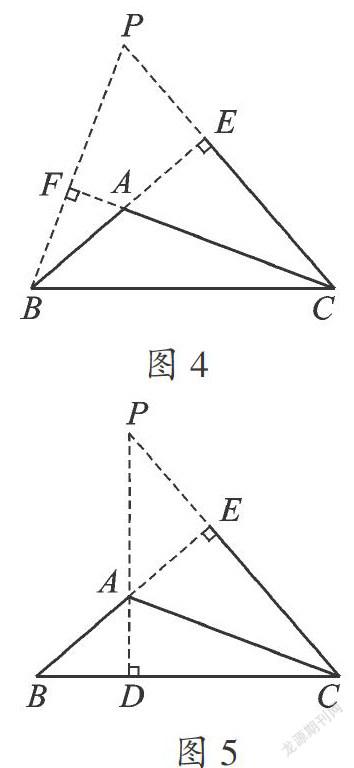
类似锐角三角形形中的图形，我们可以得到：∠BAC=180°-∠P.

②钝角△ABC的一条内部与一条外部高的延长线的夹角.如图5，在△ABC中，AD⊥BC，CE⊥AB，求∠P与∠B的关系.

由AD⊥BC，CE⊥AB得∠PEA=∠ADB=90°，∠PAE与∠BAD是对顶角，所以∠PAE=∠BAD，再由三角形内角和可得∠P=∠B.

在直角三角形中

①两条直角边（高）的夹角.

如图6，在△ABC中，AB⊥BC，那么两高 AB、BC的夹角∠B与△ABC第三个锐角∠B为同一个角.

②一条直角边（高）与斜边上的高的夹角.在△ABC中，BD⊥AC，AB⊥BC，求BD与AB的夹角∠ABD与∠C的关系.

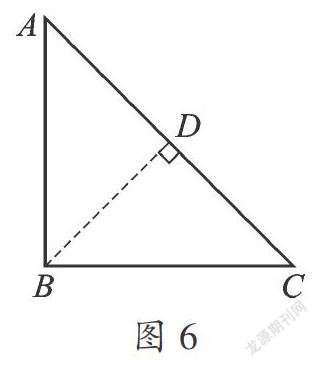
由BD⊥AC，AB⊥BC得∠ADB=∠ABC=90°，∠A是△ABD和△ABC的公共角，再由三角形内角和可得∠ABD=∠C.

结合上面各种情形的分析，探究得出的结论是：三角形的两条边上的高的夹角与三角形第三边所对的角相等或互补.

（指导老师：浦长宇）