旋转的铅笔
宋阳光
要说最有趣的教科书,非数学书莫属了!在这里,你不仅可以看到各式各类的问题,可以找到各种各样与生活相关的案例.因此,闲暇时光,我喜欢抱着数学书琢磨.比如在《平面图形的认知(二)》中有这么一个问题:
如图,铅笔放置在△ABC的边AB上,笔尖方向为点A到点B的方向.把铅笔依次绕点A、点C、点B按逆时针方向旋转∠A、∠B、∠C的度数,笔尖方向发生了怎样的变化?这种变化说明了什么?
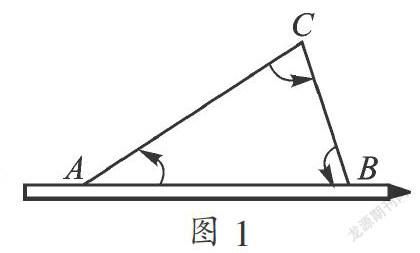
这个题目大家肯定都做过吧,按要求转动后,铅笔的笔尖向左了,也就是和原来的笔尖方向是相反的,铅笔旋转了一个平角度数,即180°.在这个变化过程说明,铅笔连续转动的∠A、∠B、∠C的度数和是180°,也就是说明了三角形的内角和是180°.
只要动动铅笔,数学问题就能解决,是不是很有趣?和大家再分享两个类似的问题.
面对这个问题,许多人的第一反应便是考虑多边形的内角和、外角和一步步推导,肯定会很麻烦,因此我们可以尝试使用上面旋转铅笔的方法.
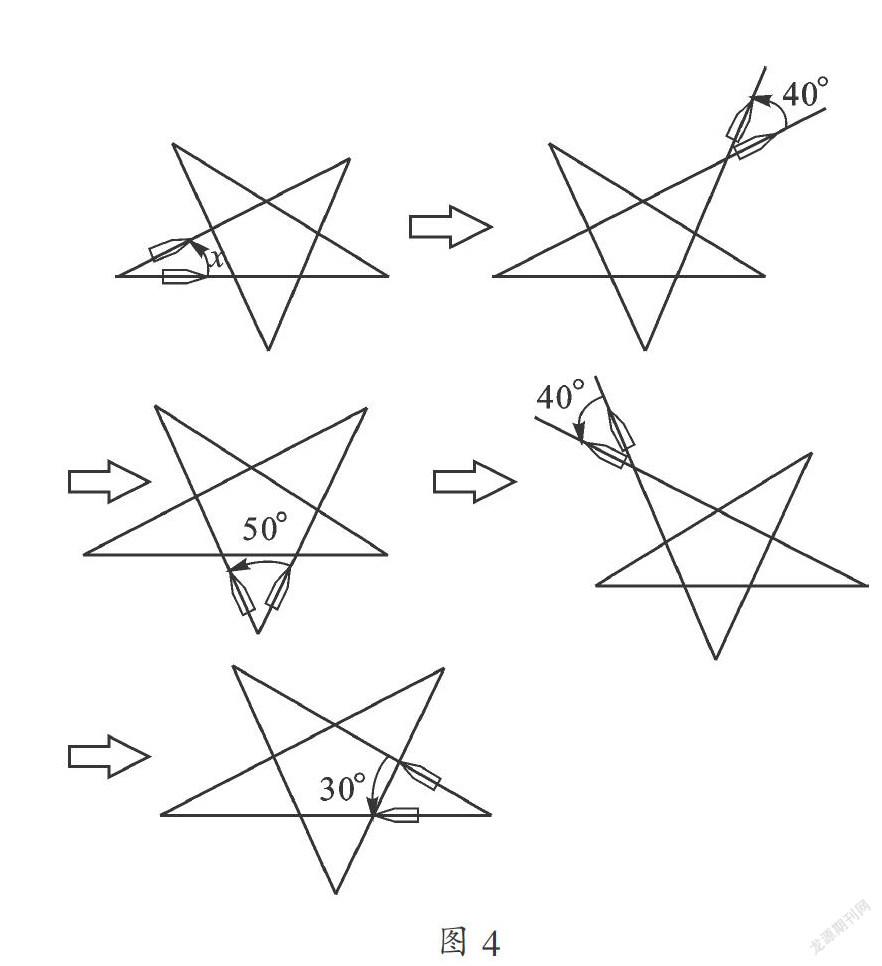
答:(1)我们以逆时针方向来转动铅笔.首先,如下图从x的地方开始逆时针转动,就会到达一个新的边上.然后,将铅笔移到此边的另一端再逆时针转动40°,就会移到另一个新的边上.在此边的另一端再逆时针转动50°,如此下去接着逆时针转动40°、30°,最后就会回到原来的边上.此时铅笔转动的方向与原来的方向是相反的.也就是说,铅笔刚好转动了半圈.因此,把刚刚转动的所有角度加起来,就正好是180°.
借这个有趣的方法,就可得到x = 180°-40°-40°-50°-30°=20°.
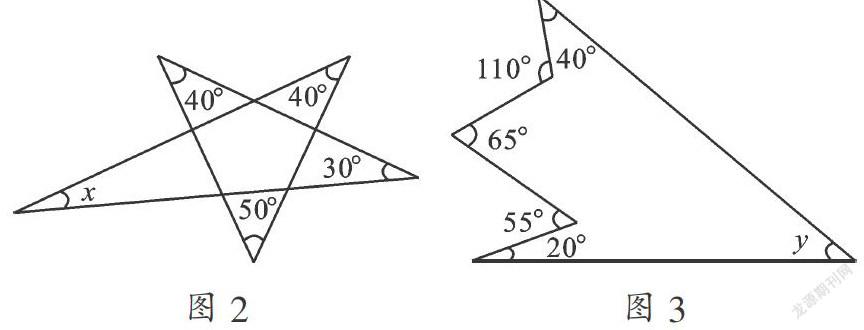
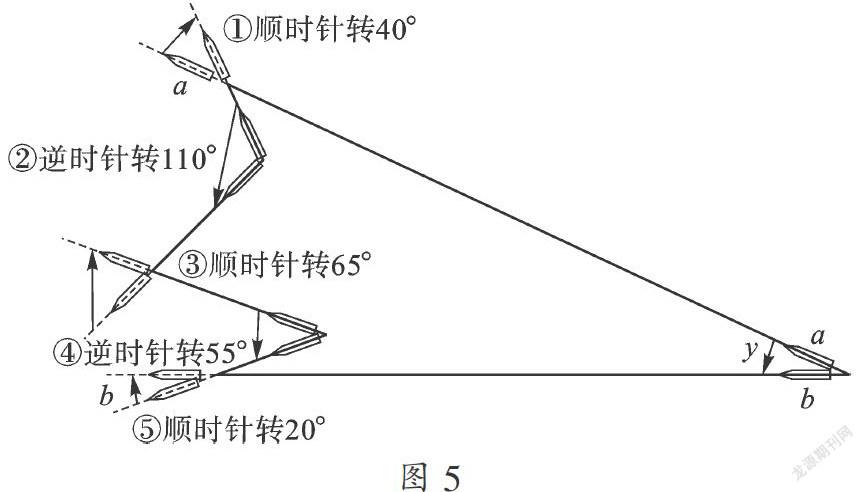
(2)下图中由A边转到B边的y的转动角度,以左侧锯齿状的部分来表示.
保持A的方向不变,往上移动.然后如①做转动,接着往下移动,然后做②的转动……最后就如⑤做转动,就会变为跟B同样方向.也就是说,由A到B转动的角度,与动作①到⑤的转动角度是相同的.把逆时针方向记为正角度,顺时针方向记为负角度,那么y=110°+55°-(40°+65°+20°)=40°
利用这个原理,我们还可以轻松验证“多边形外角和为360°”的定理,并由此推出正多边形的外角、内角……诸如此类,凡是与多边形角度有关的问题,“旋转铅笔”这个方法都可以或多或少的帮助你.
是不是很奇妙?当你的铅笔无法在推导公式上延续,不妨旋转你的铅笔,说不定你忠实的双手会告诉你准确的答案.
旋转铅笔的妙用,就是在你面对求多边形角度的问题的时候,可以省却漫长的推导,在理清楚步骤之后便可轻松解决.
若想在数学的海洋畅游,不仅需要先辈留给你的各种定理、工具,更需要你的使用和创造.记住,善用你的双手是另一条通往成功的道路!
(指导老师:浦长宇)

