厘清三线八角 掌握两线平行
魏宏
当迎春花开了,我们也就进入初中七年级下册的第一章《平面图形的认识(二) 》学习了,这就需要同学们去熟悉一张基本图形——三线八角;理解一个概念——平行线;掌握平行线的3条判定、3条性质,以上内容掌握将有助于同学们更快地走进几何图形的学习.那么,什么是平行线?平行线的性质、判定又是怎样的呢?
一、三线八角
两条直线被第三条直线所截形成八个角,
它们构成了同位角、内错角和同旁内角.
如图,直线a、b被直线 所截

①∠1和∠5在截线 的同侧,同在被截直线a、b的上方,叫做同位角(位置相同).还有∠2和∠6,∠3和∠7,∠4和∠8.
②∠5和∠3在截线 的两旁(交错),在被截直线a、b之间(内),叫做内错角(位置在内且交错).还有∠4和∠6.
③∠5和∠4在截线 的同侧,在被截直线a、b之间(内),叫做同旁内角.还有∠3和∠6.
理解三线八角,我们要把握以下几点:
1、三线八角
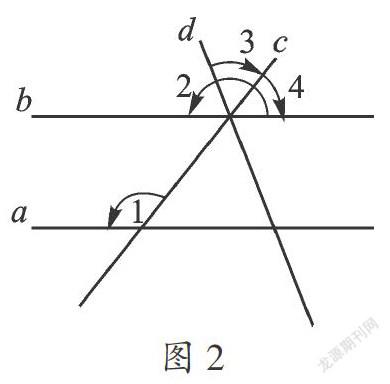
都是就两条直线被第三条直线所截这种情况下,不同顶点的两个角之间的位置而言的.如图,∠1和∠2虽然是不同顶点的两个角,但不是两条直线被第三条直线所截得的角,故不属于“三线八角”中的任何一类角.∠2和∠3虽是由两条直线被第三条直线所截而成的角,但它们同顶点,故也不属于“三线八角”中的任何一类角.
2、 三线八角讲的只是位置关系,而不是大小
关系,切不可误认为同位角、内错角必相等,同旁内角必互补.
3、 一个角可以同时
和几个角是同位角、内错角、同旁内角.如图,∠1和∠3、∠2是同位角,和∠4是同旁内角,和∠5是内错角.

二、概念来袭
1.平行线的概念
在同一平面内,不相交的两条直线叫做平行线.
2.平行线的判定

在运用平行线的判定时,一定要看清是哪两条直线被哪一条直线所截而成的同位角相等,或内错角相等,或同旁内角互补,才能正确判断是哪两条直线平行.三线八角中的“角”担任了平行线的“裁判员”.
3.平行线的性质
(1)两直线平行,同位角相等;
(2)两直线平行,内错角相等;
(3)两直线平行,同旁内角互补.

在理解平行线的性质时,一定要记住:“要使同位角或内错角相等,同旁内角互补”成立的前提条件是“已知两直线平行”.
三、概念活用
例1 如图,判断下列各对角是哪两条直线被哪条直线所截而成的什么角:⑴∠1和∠2;⑵∠1和∠3;⑶∠1和∠BAD;⑷∠2和∠4.
【解析】如图,∠1和∠2有一条公共边AB,另一边分别是AC、BC, 分离出基本图形如图.这样就构造出了一个很熟悉的“三线八角”,对照基本图形,易知∠1和∠2是直线AC、BC被直线AB所截而成的同旁内角;同样,我们可以把图中的∠1和∠3、∠1和∠BAD、∠2和∠4 分别分离出来,如下面三张图:
【答案】如图,∠1和∠2是直线AC、BC被直线AB所截而成的同旁内角,∠1和∠3是直线AB、CD被直线BC所截而成的同位角,∠1和∠BAD是直线AD、BC被直线AB所截而成的同旁内角、∠2和∠4是直线AB、CD被直线AC所截而成的内错角.

【点评】解决这类问题要熟悉“三线八角”的基本模型,根据其位置特征,可总结为:同位角是“F”型;内错角是“Z”型;同旁内角是“U”型.学会从原图中分离出基本图形,不仅为识别“三线八角”提供了方便,也为以后解决更复杂的几何问题奠定了坚实的基础.
【解析】首先由已知EF∥AD,根据两直线平行,同位角相等可得∠2=∠3,再由∠1=∠2,利用等量代换可得∠1=∠3,根据内错角相等,两直线平行可得AB∥DG,再根据两直线平行,同旁内角互补可得∠BAC+∠AGD=180°,进而得到答案.
【答案】∠3,两直线平行,同位角相等;DG,内错角相等,两直线平行;∠AGD,两直线平行,同旁内角互补;110°.

【点评】平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.见到“特殊位置”的角相等或互补,就应该想一想否有平行线的出现.反之,遇见直线平行就应联想到角相等或互补.
同学们,你们现在对“三线八角”和平行线的性质与判定有了一个更深入的理解了吗?当然,我们同时也要知道,平行线的判定还不止这些,那么,还有哪些呢?这个问题就留给你们自己思考吧!

