掌握基本知识 轻松解决问题

中考中经常会涉及到平面图形的认识（一）中的问题，这些问题难度不大，但我们也要掌握好基本知识，才能迅速准确解决。

一、有关“角”的问题

由三角板的直角顶点在直线l上，根据平角的定义可知∠1与∠2互余，又∠1=40°，即可求得∠2的度数.

【解答】如图，三角板的直角顶点在直线l上，

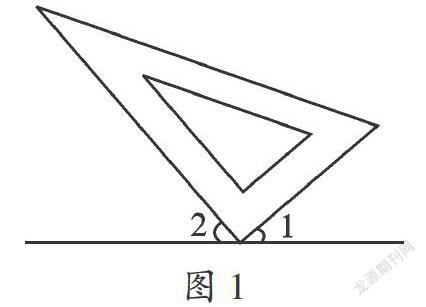
【点评】本题只要平角、互余的定义即可解决问题，是基础题，熟记互为余角的两个角的和等于90°是解题的关键.

【点评】本题考查了角的单位：度分秒的换算。由高级单位变成低级单位乘以进率，由低级单位变成高级单位除以进率。

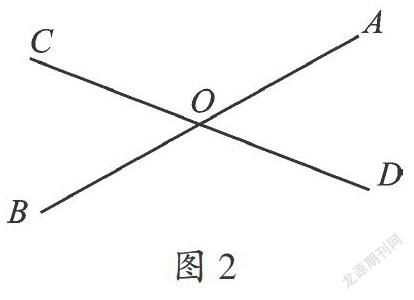
【点评】本题考查了对顶角与邻补角，对顶角相等是解题关键

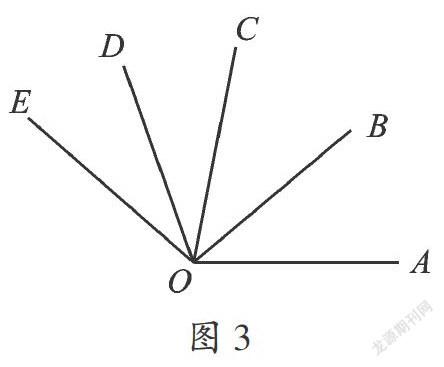
【分析】先根据OB是∠AOC的角平分线，OD是∠COE的角平分线，∠AOB=40°，∠COE=60°求出∠BOC与∠COD的度数，再根据∠BOD=∠BOC+∠COD即可得出结论.

【点评】本题考查的是角的计算，熟知角平分线的定义是解答此题的关键.

二、有关“线”的问题

【解答】C

【点评】本题属于找规律的问题，它建立在直线与直线的交点的个数变化之上，我们应该从特殊情形考虑，进而总结归纳出规律。

例5.（2014济宁）把一条弯曲的公路改成直道，可以缩短路程.用几何知识解释其道理正确的是（ ）

A. 两点确定一条直线 B. 垂线段最短

C. 两点之间线段最短 D. 三角形两边之和大于第三边

【分析】此题为数学知识的应用，由题意把一条弯曲的公路改成直道，肯定要尽量缩短两地之间的里程，就用到两点间线段最短定理.

【解答】要想缩短两地之间的里程，就尽量是两地在一条直线上，因为两点间线段最短.

【点评】紧紧抓住角的和差表示，结合角平分线的定义，运用从特殊到一般的思想方法，问题则会化难为易。

例7.如图，已知数轴上点A表示的数为8，B是数轴上一点，且AB=14.动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t>0）秒.

（1）写出数轴上点B表示的数 ；点P表示的数 （用含t的代数式表示）；

（2）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，问点P运动多少秒时追上点Q？

（3）若M为AP的中点，N为PB的中点.点P在运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由；若不变，请你画出图形，并求出线段MN的长.

【分析】（1）根据已知可得B点表示的数为8-14；点P表示的数为8-5t；

（2）点P运动x秒时，在点C处追上点Q，则AC=5x，BC=3x，根据AC-BC=AB，列出方程求解即可；

（3）分①当点P在点A、B两点之间运动时，②当点P运动到点B的左侧时，利用中点的定义和线段的和差求出MN的长即可.

【点评】本题属于一道综合题，不仅用到了线段的知识，还结合数轴、方程、两点之间的距离等相关知识，同时还运用了初中阶段经常遇到的一钟数学思想方法——分类讨论。