中心极限定理的教学

李红英

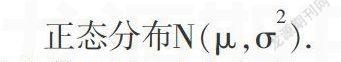
摘 要： 中心极限定理是概率论与数理统计课程中一个重要的定理，也是学生学习过程中的难点，因此教学也有一定的难度.本文首先分析学生学习的主要困惑，其次针对性地理解了中心极限定理的实质，教学过程中设计了具体事例鼓励学生自主发现探索，从而对中心极限定理容易接受，最后用实例巩固中心极限定理的应用.

关键词： 中心极限定理 正态分布 自主探索 概率近似

中心极限定理是概率论与数理统计课程中一个重要的定理，衔接着概率论知识与数理统计的相关知识，是教学中的一个难点.利用中心极限定理，数理统计中许多纷乱复杂的随机变量序列和的分布都可以用正态分布进行近似，而正态分布有着许多完美的结论，从而可以获得实用且简单的统计分析方法和结论.然而，由于中心极限定理的教学课时少而定理本身又较抽象，学生很难在短时间内理解该定理并能够加以应用.为此，不少教师对该内容进行了探讨.本文结合学生的基础和知识结构，产生的疑惑，以及教学的需要，提高学生的应用能力，对该定理的教学方法进行探讨.

一、学生学习中心极限定理的困难

中心极限定理这一节的教学目标是要求学生理解中心极限定理，并熟练运用该定理进行事件概率的近似计算，然而在讲解这一内容只有2个课时，学生又不熟悉相应的概率基础，导致无论是数学专业还是非数学专业的学生对该知识点都存在疑惑，主要表现在：不知道中心极限定理是什么意思，具体形式是什么，怎么用.针对这三方面的问题，教师首先应该要理解深刻，概括恰当，简明扼要.

1.中心极限定理的背景

在实际问题中，许多随机现象都是由大量微小的相互独立的随机因素综合影响所产生的，比如误差受到材料、环境、设备、操作者等因素的影响，每个因素都是微小的、随机的，但综合起来就产生实验过程中的误差，即误差是大量的随机因素的总和，我们关心误差就是关心大量独立随机变量和的问题.中心极限定理告诉我们，大量独立随机变量和的极限分布是正态分布.这一点突出了正态分布在概率论与数理统计中的重要地位，在应用中凸显了正态分布的许多优势，同时在总体为非正态的统计问题中发挥着重要的指导作用.在实际问题中，首先分析随机现象，将其可分解成大量的随机变量的和，那么无论随机变量服从正态还是非正态，其和近似看做正态分布，进而求相关的概率计算问题.学生对此不理解，主要是因为太抽象、太笼统，在教学中可让学生自主探讨，发现总结.

2.中心极限定理的具体形式

中心极限定理探讨的是随机变量和的极限分布，教材中给出了不同条件下的中心极限定理的多种结论，其形式复杂，证明繁琐，但总结起来本质是一个形式.

棣莫佛-拉普拉斯中心极限定理是Lindeberg-Levy中心极限定理的特例，两个中心极限定理归根到底是说独立同分布的随机变量和的极限分布为正态分布，可变形为标准正态分布.

3.中心极限定理的应用

学生对中心极限定理内容不理解，也导致无法将理论用于实践，偶尔的依葫芦画瓢并没有掌握其实质.中心极限定理常用作概率近似计算，需要根据问题的实际含义定义多个随机变量并给出分布，然后变为独立随机变量和，再利用中心极限定理和正态分布的查表求概率.只有在教学中选择恰当的例题，深入分析，合理总结，才能取到良好的效果.

中心极限定理包含极限理论，因此理论上利用中心极限定理处理极限问题.在经济问题中，质检问题中也有广泛的应用.教学中可引申生活实际等有趣的问题，让学生体会学以致用的乐趣.

二、中心极限定理的教学设计

首先利用简单的引例，让学生自主探索，总结规律.

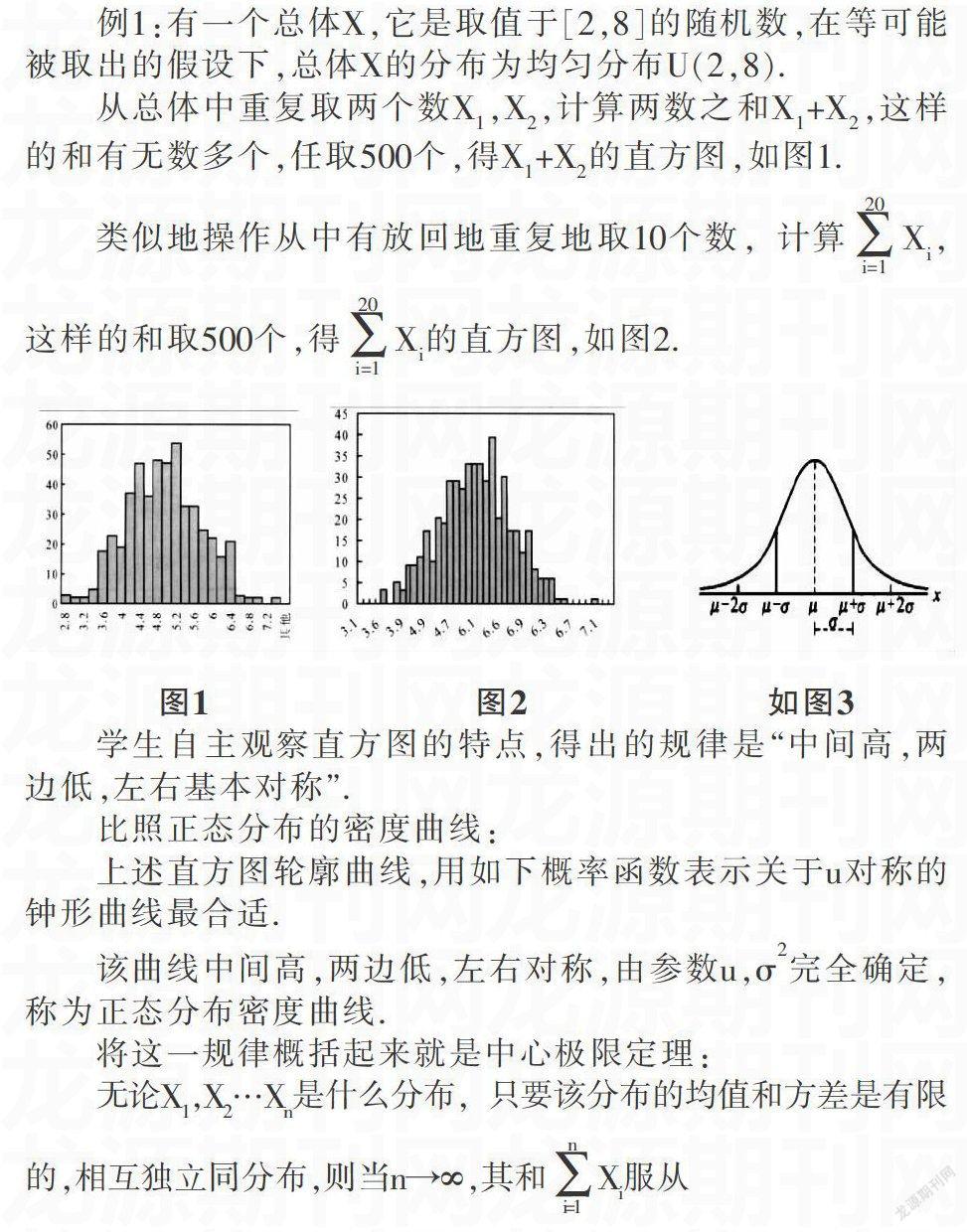
例1：有一个总体X，它是取值于[2，8]的随机数，在等可能被取出的假设下，总体X的分布为均匀分布U（2，8）.

学生自主观察直方图的特点，得出的规律是“中间高，两边低，左右基本对称”.

比照正态分布的密度曲线：

上述直方圖轮廓曲线，用如下概率函数表示关于u对称的钟形曲线最合适.

将这一规律概括起来就是中心极限定理：

其具体形式体现出三个定理.

（1）中心极限定理是用极限理论反映的一个重要定理，其优势体现在非正态分布或不知道分布类型时，为数理统计的学习奠定基础.

（2）主要应用两方面：第一，求随机变量之和落在某区间的概率；第二，已知随机变量之和的概率，求.

（3）解题中分析随机总体可分解为许多独立随机变量的和的形式甚为关键.

例2：某保险公司有2500个人参加保险，每人每年付1200元保险费，在一年内一个人死亡的概率为0.002，死亡时其家属可向保险公司领得20万元，问保险公司亏本的概率.

学生处理实际问题的难点就在于不知如何进行问题的转化.提示两点：第一，将问题用随机变量表示，每个人参保是随机的独立的，如何刻画？第二，保险公司所得的总收益如何表示，学生经整理后发现，所求总收益正好可以看成2500个独立同分布随机变量之和，n=2500足够大，故想到用中心极限定理将其近似为正态分布.求出变量和的期望和方差，利用正态分布查表求概率.

为了加强对中心极限定理的理解和巩固，对学生提出如下思考：

2.列举贴近生活实例，让学生巩固练习，加以总结.

3.学有余力拓展中心极限定理的应用领域.

通过本节的学习，让学生自主发现规律，善于总结，容易接受，形成解决实际问题的统计思维，熟悉中心极限定理和正态分布相关理论很有必要.

参考文献：

[1]茆诗松，程依明，濮晓龙.概率论与数理统计教程第二版[M].北京：高等教育出版社，2011.

[2]黎玉芳.中心极限定理的教学方法探讨[J].科技教育创新，2010（24）：220-221.

[3]孙碑.中心极限定理及其在若干实际问题中的应用[J].论谈教学，2012（6）：65-67.