高效课堂源于有效追问
杨劲芳
“追问”,顾名思义是追根究底地问,是在学生基本回答教师提出的问题后,教师有针对性地“二度提问”。它是教师对学生答问结果中表现出来的问题的一种有效处理方式,目的是再次激活学生思维,促进他们深入探究,从而提高学生的学习能力。从我国春秋时期的孔子到古希腊的苏格拉底,这些大师无不是追问的高手,他们的弟子也正是在这“一问一答一追”之间悟出真理。到了现代社会,我们的教学形式和方式都发生了改变,但不变的“追问”仍然是使用得最为频繁的一种课堂教学技能,我们几乎找不到一节自始自终没有“追问”的课。
对学生来讲,课堂的追问是否有效呢?步步追问之后,能否将学生的思维引渡到更深、更广的领域呢?……这些是值得我们思考的。
一、课堂观察
下面笔者结合人教版二年级上册“用三角尺拼角”一课中几个片段为例,谈谈基于教师层面对小学数学课堂追问过程有效性的有关思考。
片段一:追问,不是“赘”问
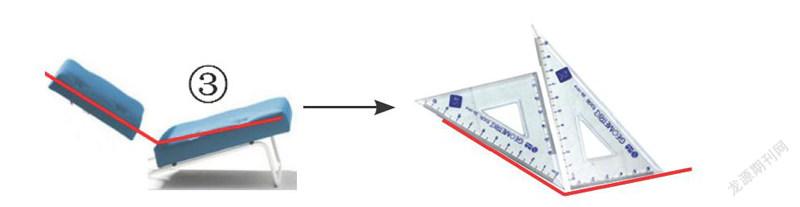
教学伊始,创设情境:在躺椅生产中,将椅背和椅面进行组装。动态形成:
师:请同学们判断一下,你觉得这三种组装,哪种更合适?
生:第三种。
师追问:为什么?
生:第一种情况人都不能坐下来,第二种只能让人坐,第三种才能让人躺下来。
师追问:那么当椅背和椅面怎样组装时才能组成“躺椅”呢?
生:坡度大一点。
生:成比较大的钝角。
师追问:为什么要成“比较大”的钝角?
生:这样躺着比较舒服。
师追问:其实这张躺椅的椅背和椅面所组成的钝角正好是由三角尺上的两个角拼成的,能猜猜是哪两个角吗?
对于二年级的学生来讲“估测”是非常难的,尤其是角度的估测,因为心中没有角度的“参照”而带来混乱局面:
——有学生认为是两个锐角拼合而成。
——有学生认为是三个同样的锐角拼合而成。
——有学生认为是直角和锐角拼合而成。
……

【思考】目标明确、任务清晰、空间广阔的探究任务是学生在探究中获得数学感悟的基点。上面的案例中教师对于“同一任务”的问题过于琐碎累赘,自然会导致学生的“目标锁定”不到位。细碎的“追问”造成了目标混沌、任务冗长,情境的引入自然是“蚂蚁骑大象”,停留在肤浅的表面了。
片段二:追问,不是“惴”问
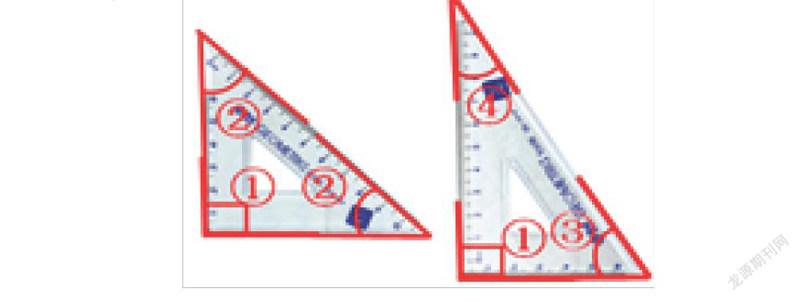
为了便于汇报,前面对三角尺中的六个角进行了编号,相同大小的角同一编号(如下图):
师:躺椅椅背和椅面的角度刚好是由∠1和∠2拼组而成的。那我们的三角尺中还可以选择哪两个角拼组成其他的角呢?
学生演示了一些组合的角,有些同学两个角的顶点没有对齐,有些同学没有将重合边对齐。……
师追问:刚才××同学拼得对吗?(学生举手不多)
怕学生答不出,教师有些惴惴不安,直接给学生看了“用三角尺如何拼角画角”的视频。
【思考】教师追问后发现学生不太理解,就急于“尾随”方法指导的视频,这样的“追问”成了害怕学生答不出的“惴问“,阻止了其他学生对于拼法的深入思考。教师“惴问”后的急于“跟进”,反馈出的不仅仅是自己的倾向性意见,更是一条羁绊学生数学思考的束带。久而久之,再有想法的脑袋也会变得僵化,其结果只能导致更多学生在课堂上不经思考的“跟随”。
片段三:追问,不是“坠”问
在学生尝试自主用三角尺的两个角进行拼角后,展示结果,呈现∠1+∠2、 ∠1+∠3、∠1+∠4、∠2+∠3、∠2+∠4五种情况。
追问:仔细观察三角尺中的角和拼组后的角,你有什么发现?
生1:我发现一个直角与一个锐角可以拼成一个钝角。
追问:还有吗?
生2:两个锐角也可以拼成一个钝角。
追问:再想想,有没有其他的情况了?
生思索,师引导:∠2+∠4这两个都是锐角,结果拼出了一个——
生3:两个锐角也可以拼成一个锐角。
……
【思考】类似这样的教学场景在课堂中可能并不少见。由于受年龄特点和经验的约束,学生的能力未达到足够水平,此时教师通过不停的追问“还有吗”“再想想”,急于牵引,让学生的回答直接“坠”入教师预设的环节中,其结果只能是“挤牙膏”。
二、反思研究
(一)明确任务——于思维发散时追出目标
如果在课堂上能保证学生思维方向、思维目标的清晰性,就可以大大缩减学生的学习时间。所以在问题的提出后,根据学生的回答,教师有意识地追问指向性一定要明确,避免不必要、不恰当的追问而让学生“绕弯路”。
【改进片段一】
师:请同学们判断一下,你觉得这三种组装,哪种更合适?
当学生明确躺椅的椅背和椅面必须成钝角后,引出这个钝角刚好是三角尺中的两个角拼组而成的,进而追问:猜一猜,可能是哪两个角拼组而成?把你的猜想记在脑海中哦,先不要说出来。
此时教师不急于请学生回答,在学生思考片刻后进行动态演示:
追问:刚才你们猜对了吗?想一想,电脑老师为什么先想到拼上一个直角?
这一追问也没有想让学生回答,但一个学生迫不及待要说:这样剩下角的大小就比较容易估计了。
在课的起始阶段,目的是引出生活当中有许多角是可以由三角尺上的角拼组而成的,并非要搞清楚是由“哪两个角拼成”。所以有时候的追问可以“欲语还休”,“犹抱琵琶半遮面”或许更能激起学生后续思维的火花。
(二)放慢速度——于思维受阻时追出时间
学生因为思路遇到障碍和矛盾而产生“断层”时,不能进一步地进行深层次的思考,使得回答暂时停顿。这时,教师不要急于拿出事先的“标准答案”,要放慢速度,给学生留足思考时间后再进行追问,进一步引导。
【改进片段二】
师:躺椅椅背和椅面的角度刚好是由∠1和∠2拼组而成的。那我们的三角尺中还可以选择哪两个角拼组成其他的角呢?
生:∠1和∠3,∠2和∠4拼组。……(略)
师:请你拼给大家看看。(生演示)
师故意放大学生的不规范操作:
追问:这样行吗?为什么?你觉得在拼角时应该提醒自己注意什么?
生1:顶点要对齐,重合的边也要对齐。
生2:跟我们上节课学习的比角的大小类似,要“点对点、边对边”。
……
很明显,相比较前面片断二中的“冷场”,改进片断中多了一个“放大不规范操作”的环节,就较好地引出了学生的客观评价。而当学生充分讨论追问问题之后再观看“用三角尺如何拼角画角”的视频,感受更深了,亲身感悟后的效果也会更佳。
(三)巧设阶梯——于思维跨度间追出桥梁
学生因为先前的学习而产生单一定式时,不能进一步地进行深层次的思考,使得回答缺乏深度。这时,教师要有意识地追问,及时提供科学的思维方法,搭设思维跳板,帮助学生开拓思路,突破难点,并在更高层次上继续思考,进一步激起学生创新的火花。
【改进片段三】
学生拼角作品中呈现∠1+∠2、 ∠1+∠3、 ∠1+∠4、∠2+∠3、∠2+∠4五种情况。
追问:能将这些拼组成的角进行分类吗?怎么分?
生1:拼组后的角有锐角、直角和钝角。
师追问:哪几种情况拼出的是锐角?钝角?
根据学生回答进行归类:∠1+∠2、 ∠1+∠3、∠1+∠4、∠2+∠3——钝角;∠2+∠4——锐角。
追问:你有什么发现?
生1:直角+锐角一定能拼出一个钝角。
生2:∠2和∠3都是锐角,但也拼出一个钝角。锐角+锐角=钝角。
生3:∠2+∠4也都是锐角,但拼出的是锐角。锐角+锐角=锐角。
追问:两个锐角一定只能拼出钝角或锐角吗?有可能是直角吗?
思索片刻后,生4:∠3+∠4就能拼成一个直角。
生5:∠2+∠2也能拼成一个直角。(为了更具说服力,生4和生5分别向同桌借了一块同样的三角尺演示拼组)
追问:三角尺中有没有这样的两个角,拼组在一起组成一个不是直角、钝角和锐角的角?
经追问引导后,学生把目光锁定在两个直角的拼组上,得出:直角+直角=平角。
……

相比较前面的片段三,这一环节的改进无疑多了几个“追问层次”而已,给学生设置了一个坡度,在学生的思维跨度间架设了桥梁,顺应学生的认知结构。
课堂上我们经常会用到追问,是不是教师的每一个追问都是有效的呢?例如:“还有吗?” “再想想,还知道什么?”“就这一种吗?”“不止这些吧!”这些类似于口头禅的追问方式用在关键处有时的确能起到“推波助澜”之功效,但如果教师经常在任何需要或不需要追问的地方都不假思索地用上这些“随意追问”,那就是低效的。我们希望课堂的进程如同直升机降落时的直接高效,但我们更相信课堂的高效来自于民航机降落时的迂回与递进。追问时少一点“直线下坠”,多一些“螺旋下降”,给学生一个梯度,效果会更好。
追问,是引导学生更为深入理解数学本质的手段。它并不是一成不变的,时而需要“一蹴而就”,时而需要“细水长流”,教学时需要注意把握追问对象的差异性和渐进性,科学处理好“扶”与“放”、“进”与“停”的关系,通过多种形式对学生的思维作即时的疏导、点拨。
追问——教师的一种能力,自然、及时、有序地“问”,相信一定能将学生“追”向数学思维的深处!
(浙江省杭州市学军小学 310012)

