提高数学课堂教学质量的几种方法
张荣华


摘 要: 数学课堂教学质量与教师选择的教学方法密切相关。在教学中采用问题情境化、策略多元化、结论过程化、课堂民主化、知识应用化等教学方法,将使课堂教学效果事半功倍,学生兴致盎然,知识得到拓展,能力得到提高,思维得到训练,形成良好的情感体验,积累丰富的数学活动经验,真正成为学习的主人。
关键词: 数学问题 教学方法 数学课堂 数学结论 数学知识
课堂教学中教学策略的使用直接影响到课堂教学效果。那么,在新课程实施背景下,如何采取有效的教学策略提高数学课堂教学效率呢?笔者结合自己的教学实践谈谈做法。
一、数学问题情境化
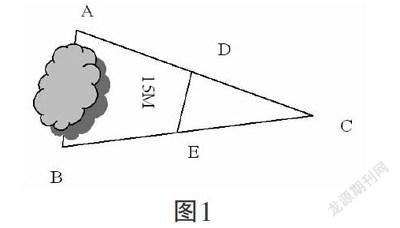
《数学课程标准》明确指出:“让学生在现实情境中体验和理解数学”。从教学实践来看,教师可以从学生熟悉的生活环境、知识背景出发,创设他们感兴趣的学习情境,寓问题于情境之中,引发学生的思考。如教学“三角形中位线”的知识时,在新课导入环节,我设计了如下情境:如图1,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,但绳子长度不够,一位初三同学帮他想了一个主意:先在地上取一个可以直接达到A、B两点的C点,再找到AC、BC的中点D、E,当测量出DE的长度为15米后,这位初三同学告诉小明,线段AB长是30米,你知道为什么吗?
图1
此问题情境蕴含着三角形中位线定理的应用,我将这一知识情境化,并通过设置悬念顺利引入本节课题——三角形中位线,水到渠成,激发了学生的好奇心和探究新知的欲望。
二、教学方法多元化
“有效的数学学习活动不能单纯地依赖模仿和记忆,动手实践、自主探索与合作交流是学生学习数学的重要方式”。教学实践中,笔者为满足学生多样化的学习需求,精心设计丰富多彩的数学活动,留给学生充分的、自主选择的余地,让他们根据学习任务的特点及自身的喜好,灵活、恰当地选用独立思考、动手实践、小组合作、探索发现等多种学习活动方式,使他们在“看一看”“摆一摆”“剪一剪”“切一切”“做一做”中真正理解和掌握基本的数学知识与技能,数学思想和方法,获得广泛的数学活动经验。如教学“从不同方向看”这一节内容时,先是引导学生用山芋、萝卜切成小正方体,再用制成的小正方体摆一摆,让处在不同方位的学生分别说说看到的是什么图形,并把它们画出来,启发学生思考:“为什么同一物品看到的模样却是不一样的?”进而揭示三视图(主视图、左视图、俯视图)的有关概念,这样既形象直观,又让人印象深刻。
三、数学结论过程化
第斯多惠有句名言:“一个坏教师奉献真理,一个好教师则教人发现真理。”数学教学中有很多的概念、定理、结论、规律都有其生长、发展、形成的过程。这一过程中教师要带领学生一起经历、共同发现,让学生亲身感受、亲耳所闻、亲眼目睹知识产生、形成、发展,最终成为结论的过程,从而加深对所学知识产生背景、形成过程、应用范围的认识和理解。如教学“绝对值”这一概念时,我设计了如下几个步骤:
(1)在数轴上找出表示4的点。(2)观察这个点到原点的距离有几个单位长度。(3)指出:数轴上表示4的点到原点距离有4个单位长度,称4的绝对值是4,记作:|4|=4。(4)你能按照这样的方法想一想-4的绝对值是几吗?(5)说一说3,-2,1.5的绝对值。(6)引导学生归纳绝对值的定义。
通过这样由浅入深、循序渐进的几个步骤,清晰展示了绝对值概念的形成过程及本质特征(即某一点到原点的距离),易于被学生理解、接受。
四、数学课堂民主化
民主化的课堂教学,是建立民主平等和谐师生关系的基石,更是培养学生发散性和创造性思维品质的重要途径。在教学实践中,教师要找准自己的角色,主动成为学生数学学习的组织者、引导者和合作者,让学生成为数学学习的主人,精心营造民主、和谐的教学氛围,鼓励学生大胆发言,敢于发表不同的见解,发展学生的求异思维。如教学完一元二次方程的解法后,出示一道题:解方程(x+1)2-9=0,当不少学生用“直接开平方法”求解后,我问:“你还能用其他方法吗?再仔细想想。”不一会儿就有学生举手要发言。生1:从结构上看,这个方程具备平方差公式的特征,因此它可分解为(x+1+3)(x+1-3)=0,整理得(x+4)(x-2)=0,求得x1=-4,x2=2。不少同学表示认同。生2:可以将左边展开,转化成一般形式,再用求根公式求解。有些学生认为这样解题变得复杂。在学生发言的基础上,我引导他们比较三种解题方法的优缺点,并让他们选择适合自己的解题方法。
五、数学知识应用化
乌申斯基指出:“空洞的毫无根据的理论是一点用处没有的,理论必须联系实际。”新课标强调要培养学生的应用意识,使学生面对实际问题时能主动尝试从数学的角度运用所学知识和方法寻找解决问题的策略,达到学以致用的目的。我在课堂教学中主要从三个层次安排知识应用。一是新课进行中针对某一知识点的巩固性练习,题量较少,一般1至2题,如教学科学计数法之后出示如下两道题:(1)3600000=()×10()(2)-0.00000036=()×10();二是新课结束后进行的综合性检测,通过填空题、选择题、判断题、解答题等不同题型考查了解学生本节课的掌握情况,便于及时查漏补缺;三是留给学生课外完成的延伸拓展题,一般与生活联系紧密,难度较大,主要考查学生综合应用能力,如教学“铁丝围矩形”这一节新课后,设置了一道思维拓展题:“在一块长32米,宽24米的矩形绿地内,要围出一个花圃,使花圃面积为矩形面积的一半,你能给出一种设计方案吗?”学生通过设计,不仅加深了对所学知识的理解,而且增强了应用意识和解决问题的能力。
在课堂教学中,教师采用数学问题情境化、教学策略多元化、数学结论过程化、课堂教学民主化、数学知识应用化等教学方法,能引起学生学习兴趣,发展学生求异思维,体现知识生长、发展、形成过程,也有利于和谐师生关系,强化新知识应用。因此,在数学教学中,应当强化这些方法的应用,促进学生数学思维、能力和素养的提升。

