Rasch模型在师范生说课技能评价中的应用研究

郭芸等

摘 要： 本文将科学测量理论的多面Ranch模型理论用于师范生说课技能评价的数据分析，为相关评价提供信效度信息，同时为未来教育测评提供有价值的参考。

关键词： 说课技能 评价 Rasch模型 加权拟合统计

说课是一种重要的教学研讨形式，说课技能训练对提高师范生教育教学水平具有重要作用，已成为师范生教学技能培训的重要组成部分。然而，在师范生说课培训实践中，师范生的说课技能评价主要依靠指导教师的主观评分确定，评价可信度相对较低。

丹麦数学家Georg Rasch于1960年提出的Rasch模型提供的统计框架可以消除主观评价中各方面因素对评价结果的影响[1]。该模型除了考生能力和试题难度两个因素外，还将评分员及评分量表等因素加入模型，不仅可以分析考生能力和试题难度导致的评价差异，而且可以分析由其他因素导致的评价误差来源，可有效提高主观评分信度[2]。

本文通过Rasch模型对说课比赛中学生的表现、评分者的评分及评分标准的难度做整体分析，从而检验是否每个学生都得到合理评估，评分者对学生的评估是否做出了合理判断及评分严厉度的差异，评分标准的难度值是否符合学生的整体能力，为师范生教学技能评价提供有益参考。

1.研究对象

以某高等师范院校生物科学（师范）专业四年级的8名师范生（其中男生3名，女生5名）的说课比赛成绩为对象，其中说课内容包括一说教材，二说教法，三说学法，四说教学过程，五说教学评价，六说板书。5位评分教师根据说课学生上述六方面的表现，按照评分标准采用10点计分，具体见表1。

2.研究方法

采用Bond & Fox Facets[3]，一种进行多面Rasch分析的计算机软件程序对上述数据资料进行分析。本研究设计了三个侧面，即学生表现、题目/任务难度、评分者的严厉度。采用的可以接受的吻合统计（infit）范围设置在0.6-1.4之间[4]。此外，学生表现评估报告分离比的期望值大于2.0[5]。

3.研究结果

3.1对评分者、学生及内容的概述

在这次说课比赛中，对学生能力、评分者严厉度和评分标准难度的总体评估结果见图1所示。图中最左侧呈现的是对数（logits）刻度，范围从-2到+4，对于三个侧面标尺都相同；学生能力以学生编号呈现在第二列，能力最高的学生在顶端，能力最低的学生在底端；评分者的严格程度在第三列，最宽松的评分者在底部，而最严格的评分者在最顶端；项目（评分标准）的难易程度在第四列，图中由上而下依次为由难而易；最后一列为评分量表的使用情况。该图可直观地显示每个侧面的整体分布及不同个体之间的差异。由图1可知，8名学生的能力排序，其中最高能力的表现者为S6，最低能力的表现者为S4；评分者中有3位在0以下，1位评分者在0处，1位在+2到+3之间，显示5位评分者中4位较宽松，一位较严格；在项目难度方面，既不容易，又不难，六个项目中一个高于平均值，三个处于平均值，两个低于平均值。

3.2学生能力表现分析

学生能力表现的估计值从-0.94logits到3.95logits（图1第2列）。按照学生表现的质量以降序排列。具体来说，能力估计值纵列显示学生6是能力水平最高为3.95logits，而学生5能力最差为-0.94logits。

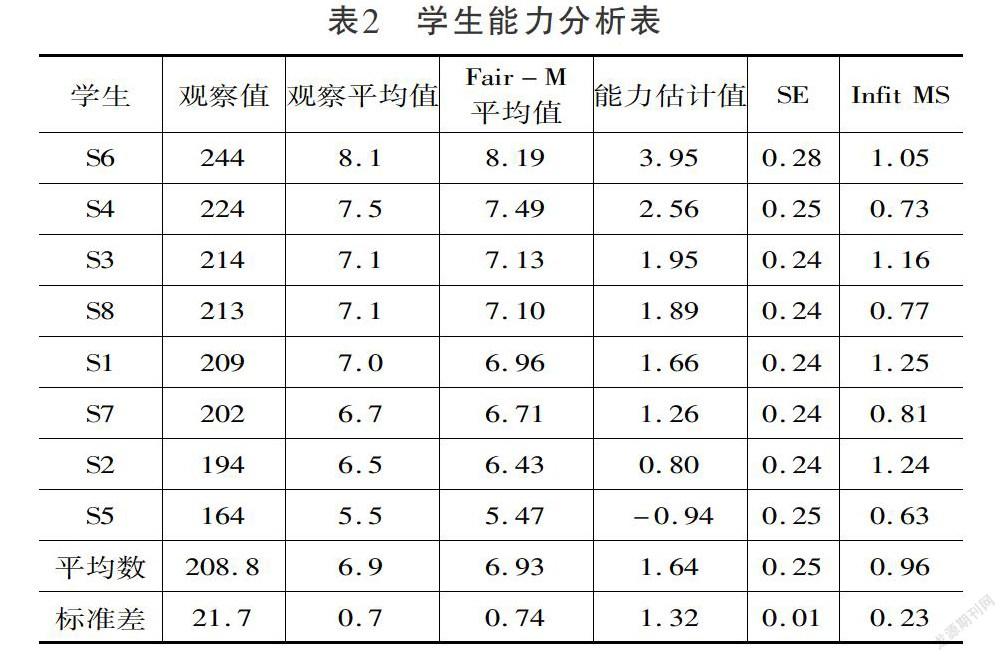
学生说课比赛中的能力表现分析的吻合统计——加权拟合统计（infit）结果见表2。在表中，拟合统计显示所有学生都拟合模型，加权拟合统计量（infit）在可接受范围内（0.6-1.4），表明每个学生都能被科学地评估，得到合理的能力分数。

多面Rasch分析也提供RMSE（Root Mean-Square Standard Error），即估计值标准误均方的平方根，代表估计的平均误差。学生能力的RMSE是0.24，表明学生的测量误差很低。分离比（Separation）取值范围在0至无穷大，达到2就能区分高低水平，学生的分离比是5.20，超过了最低要求2.0，说明依据学生的表现能够把学生的能力区分开来。上述结果说明本测验信度高，能够按照能力水平将学生区分开。

3.3评分质量分析

5个评分者的严格程度平均值为0，表明评分者的评分整体上比较适宜。对评分者评分质量的吻合统计结果见表3。按照拟合统计量可接受的范围（0.6-1.4），表明评分者对学生的表现都作出了合理判断。评分者的分离比为5.61，分离信度为0.97，这些信息表明评分者之间是存在差异的，5位评分者中至少有一位评分者在评分过程中表现出明显不同的严厉度，但总体上呈现较好的内部一致性，他们以统一标准行使自己的评判职责。

3.4项目难度分析

对项目难度分析的吻合统计结果见表4。表中项目以难度降序呈现，结果显示“项目1”是最难的项目（说教材），“项目4”在六个标准中是最容易的（说教学过程）。“说教材”成为学生说课最困难的项目，表明入职前的教师（师范生）由于缺乏对教材的系统学习与思考，未能在深入理解课程标准的基础上准确把握教材。拟合统计显示所有项目都非常吻合模型期望，各个项目的infit统计量都在0.6-1.4之间，即各评分者跨评分标准的一致性较好，各评分者在同一评分标准上的宽严标准相同。

4.讨论

在依靠主观评价学生的学业能力时，传统做法是除去一个最高分和一个最低分，评价者所给平均分就代表学生的学业能力，这样的做法往往存在局限性。评分者对评价项目的理解及要求（严厉度）存在差异，有可能给出最高分或最低分的评分者对学生的表现做出了合理判断，即检测存在样本依赖与测验依赖[6]，学生的能力无法得到客观评价。

与传统教育测量相比，Rasch模型分析可以鉴别影响主观评价可靠性的各种因素，如特殊的评分者、特殊的评分标准。同时，能够依据吻合统计（Infit）改进测验，当发现不吻合因素时，能够通过与评分者、参与学生进行讨论改进评估。本研究基于Rasch模型对师范生说课能力评价结果的分析提供三个评估侧面之间的关系（图1）、学生能力和吻合统计（表2）、评委的严格程度和吻合统计（表3）、项目难度和吻合统计（表4），模型分析的结果表明，每位学生都在吻合统计范围之内，说明每个学生都能被科学地评估，得到合理评价，其分离比说明测验信度高，能够把学生分为不同能力水平；对评分质量分析得到拟合统计量在可接受范围，证明评分者对学生的表现做出了合理判断，分离比等信息表明评分者之间存在差异，但总体上呈现较好的内部一致性；对评分标准（项目难度）的分析表明各评分者跨评分标准的一致性较好，各评分者在同一评分标准上的宽严标准相同。

参考文献：

[1]晏子.心理科学领域内的客观测量——Rasch模型之特点及发展规律[J].心理科学进展，2010，18（8）：1298-1305.

[2]Linacre JM，Wright.BD.A user’s guide to FACETS：Rasch model computer program，version 2.4 for PC compatible computers[M].Chicago，IL：MESA Press.1993.

[3]Bond TC，Fox CM.Applying the Rasch model：Fundamental measurement in the human sciences （2nded）[M].Lawrenec Erlbaum Associates Inc，2012.

[4]Wright BD，Linacre，JM，Gustafson JE，Martin-Lof P.Reasonable mean-square fit values[J].Rasch Measurement Transactions，1994，8（3）：370.

[5]Linacre，JM.Many-facet Rasch measurement.Chicago，IL：MESA Press.1993.

[6]王蕾.Rasch测量理论及在高考命题中的实证研究[J].中国考试，2008（1）：32-39.

通讯作者：龙中儿