层次分析法在林业工程项目管理中的应用
刘 峰
(河北省林业厅三北办,河北 石家庄 050081)
1AHP的基本原理
层次分析法(AHP),又称多层次权重解析法,是美国运筹学家匹茨堡大学教授萨蒂(T-LSaaty)于20世纪70年代初,提出的一种层次权重决策分析方法。其基本原理就是把决策问题看作一个系统,按照总目标、子目标、直至具体方案的顺序,构造一个能够反映系统内在联系的阶梯层次结构模型。并将层次内因素两两进行比较构成判断矩阵,利用求解判断矩阵特征向量的办法,求得每一层次的各元素对上一层次某元素的优先权重,最后通过递阶层次权重解析得到方案层对总目标的最终权重。这里“优先权重”表明的是各备选方案在某一特点的评价准则或子目标下优越程度的相对量度,以及各子目标对上一层目标而言重要程度的相对量度。层次分析法比较适合于具有分层交错评价指标的目标系统,而且目标值又难于定量描述的决策问题。
2AHP的具体步骤
2.1 建立层次结构模型
系统总体划分为3个层次,最高层为目标层,只包含1个元素,表示系统总目标;中间层为准则层或指标层,可以有1个或几个层次,包含多个元素,表示实现总目标所涉及到的各子目标(考虑到过多元素会给主观判断比较带来困难,一般每层元素不超过9个);最下层为方案或对象层,表示实现各决策目标的可行方案。可表示如图1。
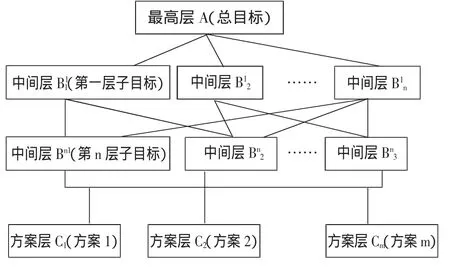
图1 层次结构模型
2.2 构造判断矩阵
判断矩阵是针对上一层次中的某元素而言,评定该层次中各有关元素相对重要性程度的判断。AHP法采取了以两两重要性程度之比的形式来表示两个因素的相应重要性程度等级,将两两比较结果构成判断矩阵。
为了提供更为准确的比较数据,Saaty给出9个重要性等级及其赋值(表1)。

表1 判断矩阵标度及其含义
2.3 层次单排序并做一致性检验
对于判断矩阵A,计算满足AW=λmax*W的特征根和特征向量。在上式中,λmax为判断矩阵A的最大特征根,W为对应于λmax的特征向量,W的分量Wi就是对应元素单排序的权重值。判断矩阵的一般求解方法有根法、和法及幂法,计算过程均可以借助计算机完成,在此不作具体介绍。
为了检验判断矩阵的一致性,需要计算它的一致性指标即:CI=(λmax-n)/(n-1)。当CI=0时,判断矩阵具有完全一致性;反之,CI值愈大,就表示判断矩阵的一致性越差。为了检验判断矩阵是否具有令人满意的一致性,需要将CI与平均随机一致性指标RI进行比较(表2),CI与同阶的平均随机一致性指标RI之比,称为判断矩阵的随机一致性比例,记为CR。一般地,当CR<0.1时,就认为判断矩阵具有令人满意的一致性;否则,当CR>0.1时,就需要对判断矩阵进行修正,直到满意为止。

表2 平均随机一致性指标
2.4 层次总排序
层次总排序是从上至下逐层进行的,即递阶层次结构权重解析。对于第k层关于总目标A的优先权重向量的计算可做如下表述:将第k层求得的每个元素对应上一层相关元素的权重向量作为列向量组成一个矩阵记为Pk,则第k层子目标关于总目标A的优先权重向量Wk=Pk*Wk-1,其中Wk-1为上一个层次(k-1层)各子目标关于总目标A的优先权重向量。相应的,如果测评系统共n层,则最终方案层对应总目标的优先权重向量为Wn=Pn*Wn-1,该向量的各个分量即为对应各方案对总目标的优先权重,值最大者即为最优方案。
3 林业项目管理在应用AHP时应考虑的重点问题
通过上述分析不难发现,应用AHP法进行决策,最重要的环节,一是层次结构模型的构建;二是判断矩阵的构建,这2个环节是AHP的核心,其科学与否决定了最终决策结果。林业项目在应用AHP时应重点考虑的也同样是这两个问题。
3.1 一般林业工程项目AHP层次结构模型
考量林业项目实施方案的科学性,主要从项目预期效益、投资能力、技术措施、保障能力等4个方面入手,在每个一级指标下,可根据具体项目建设方向、特定要求确定不同的下层指标。一般地可构建如表3所示层次结构。
考虑到设置元素过多,会给主观判断比较带来困难,在实际操作中,要针对具体的项目特点,尽量简化指标系统。对于影响度很小的因素应予删除,能够合并利用一个指标来评价的多个因素,尽量合并。如项目区的生态区位特点、社会经济发展需求等指标,与预期效益指标往往具有同一性,可以合并考量。又如,某项目是由中央全额投资,对其他投入不做要求,那么地方配套和社会融资指标就没有设置必要;如果项目建设以生态效益为主,兼顾社会效益,对经济收益不做任何要求,就不必设置经济效益指标。
3.2 构建判断矩阵应注重的问题
建立判断矩阵需要对一个层次中的每一个元素与其他元素进行两两比较,对元素重要性程度的准确把握是判断矩阵科学准确的前提。因此,决策者在选择项目评审专家时,应考虑其具备以下三个必要条件:一是明晰项目建设内容,能够准确把握项目建设方向、建设布局、投资来源,以及项目质量、进度等硬性技术指标。二是熟悉项目区或承担单位情况,包括项目区自然和社会经济条件、生态建设基础、党政领导组织能力、财政状况、林业技术及项目管理水平、群众参与度等。三是具有丰富的行业经验,精通专业技术,对项目建设前景、行业发展现状有准确的认识,对林业政策法规、相关市场情况等外部环境都有深入的了解。
4 林业项目计划管理AHP法范例分析
假设有某林业建设示范性项目,要求在水土保持重点区完成容器苗示范造林66.7hm2,项目主体功能为生态防护功能,能够有效提高带动相关区域对水土保持林建设及容器苗造林技术应用的重视程度与推进力度。项目投资为中央资金全额投入,投资规模控制在100万元以内,在现有3个备选方案当中选择最合理方案。备选方案基本特点如表4。
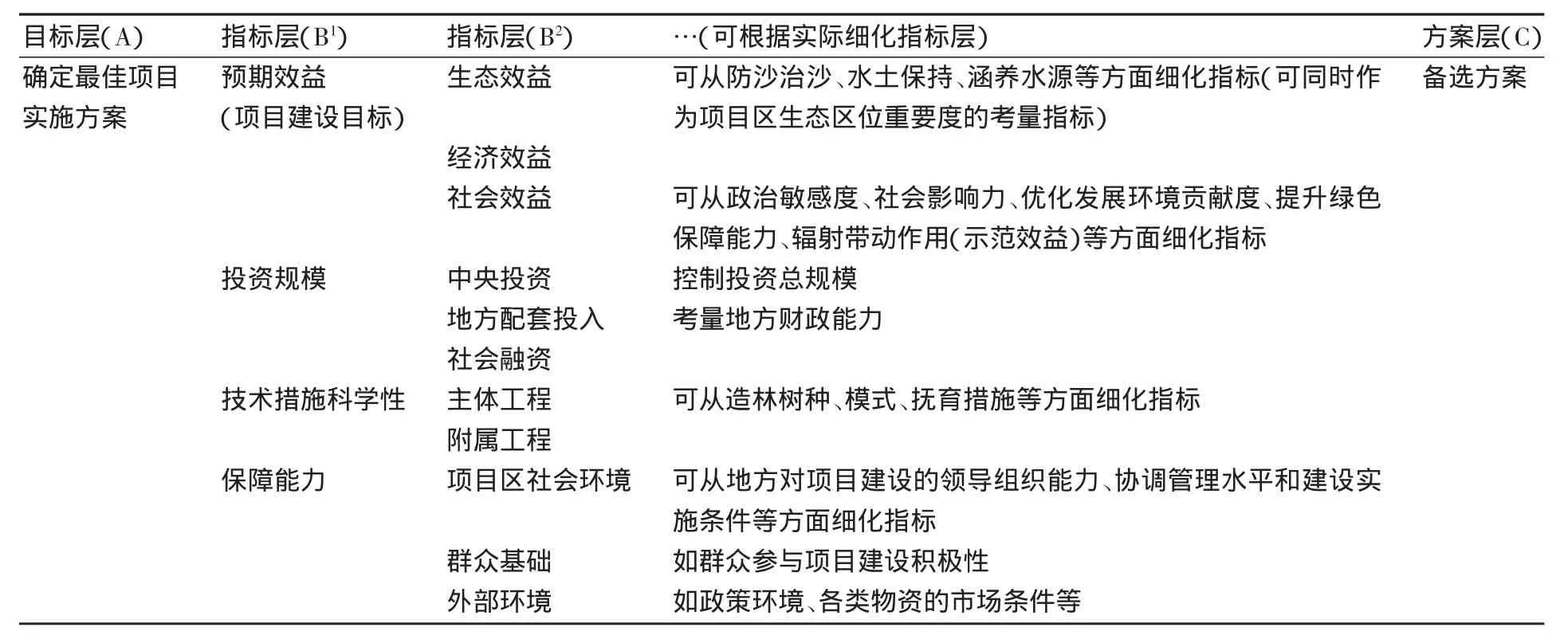
表3 一般林业工程项目AHP层次结构

表4 某林业项目3个备选方案基本特点
4.1 构建层次结构模型
因为项目规模较小,预期效益目标、投资来源单纯,影响因素构成比较简单,在此采用一个指标层即可,并构建如表5层次结构系统。

表5 某林业项目测评指标体系
4.2 判断矩阵构建与权值排序计算
4.2.1 第一层构建与权值排序计算
计算求得:
特征向量 W1=(0.23087,0.55085,0.04966,0.08431,0.08431)T,即可得到对应各因素权值。
最大特征值λmax=5.0492,经一致性检验,CI=(λmax-5)/4=0.0123,CR=CI/RI=0.0123/1.12=0.011<0.1,所以判断矩阵满足一致性检验(表5)。
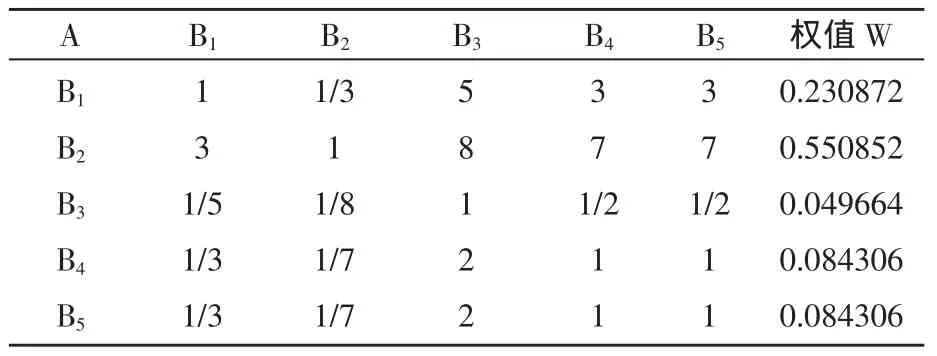
表5 矩阵A-B
4.2.2 第二层判断矩阵构建与权值排序计算(表6~10)
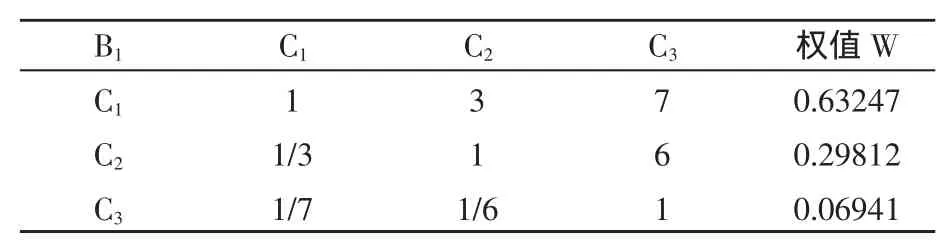
表6 矩阵B1-C
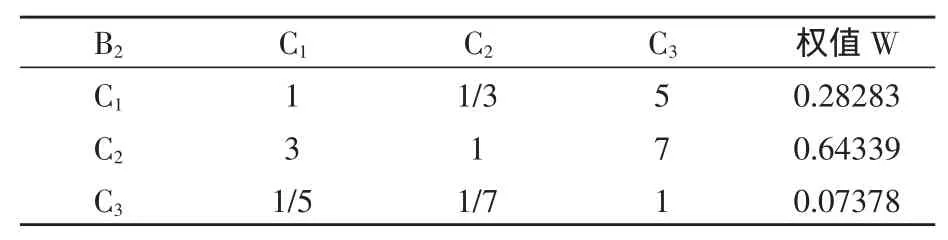
表7 矩阵B2-C
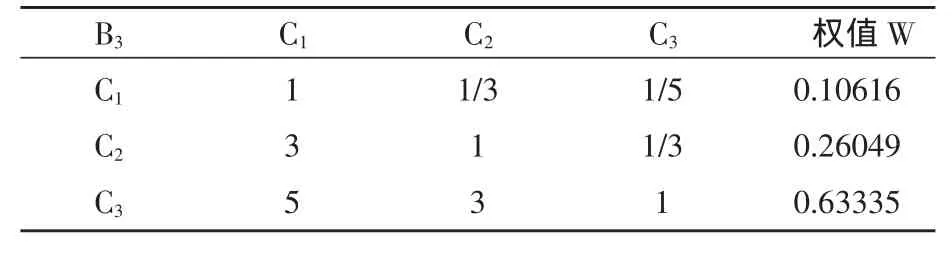
表8 矩阵B3-C
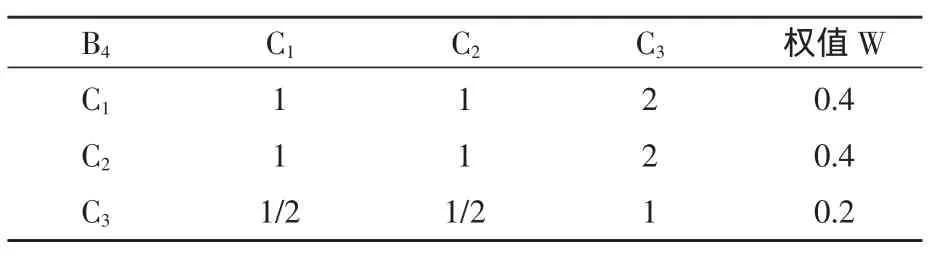
表9 矩阵B4-C
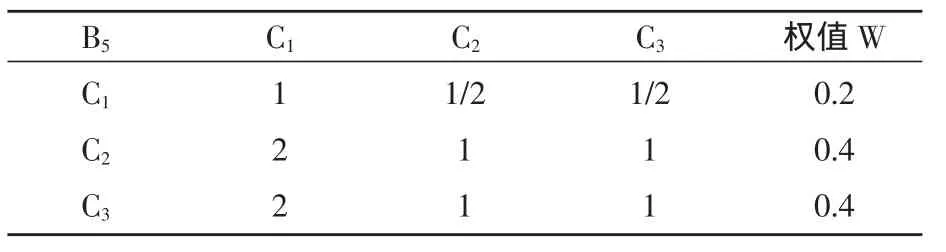
表10 矩阵B5-C
4.3 层次总排序
将第二层3个方案对应的5个子目标所得的5组优先权重向量组合成矩阵P,则有
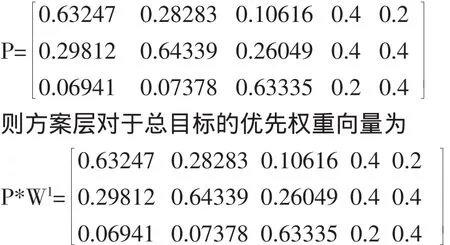

由此可见3个备选方案对总目标的权重排序结果为:C2>C1>C3。方案2为项目实施最佳方案。
5 结论
(1)在林业工程项目计划管理中,通过AHP法能够将各类影响因素进行系统化、条理化,把多目标、多准则又难以全部量化处理的决策问题化为多层次单目标问题,并通过成对比较判断进行量化分析,为决策者提供更清晰可靠的依据。方法简便易行,数学原理简单,计算过程可全部由计算机完成,易于掌握。
(2)AHP法不足之处在于使用该方法并不能为决策者提供新的更好的方案,只能够在现有方案中选择,并且该方法对专家学者技术水平和行业经验有较高要求,在缺乏合适专家的情况下,不能应用该方法。
[1]张炳江.层次分析法及其应用案例[M].北京:电子工业出版社,2014.
[2]陈森.层次分析法在林业生产决策中的应用[J].中南林业调查规划,1993,(4).

