烧结矿余热回收竖罐内气固传热特性
冯军胜,董辉,刘靖宇,梁凯
(东北大学材料与冶金学院,国家环境保护生态工业重点实验室,辽宁 沈阳 110819)
烧结矿余热回收竖罐内气固传热特性
冯军胜,董辉,刘靖宇,梁凯
(东北大学材料与冶金学院,国家环境保护生态工业重点实验室,辽宁 沈阳 110819)
以自制气固传热实验装置为操作平台,实验研究了烧结矿颗粒填充床内的气固传热特性。结果表明:气体表观流速和烧结矿颗粒直径是影响颗粒床层内气固传热过程的主要因素。气体表观流速越大,颗粒直径越小,床层内气固传热系数就越大。当烧结矿颗粒直径和气体表观流速一定时,床层内烧结矿颗粒温度的升高导致床层气固传热系数的增加和传热Nusselt数的减小。由于计算误差较大,现有的经验关联式不适用于求解烧结矿颗粒床层内的气固传热过程。基于量纲分析法,并结合实验测量数据拟合得出了能够描述烧结矿颗粒床层内气固传热特性的实验关联式,平均计算误差为4.22%,显示了良好的预测性能。
烧结;填充床;竖罐;多孔介质;传热系数
引 言
烧结过程余热资源的高效回收利用是目前降低烧结工序能耗的主要途径之一[1]。烧结矿余热罐式回收是针对现有烧结余热回收系统存在难以克服的弊端[2],借鉴干熄焦炉的结构和工艺提出的一种烧结余热高效回收方式[3-6]。就床层特点而言,烧结矿余热回收竖罐是一种随机非结构化大颗粒填充床,床层内烧结矿的填充结构近似于多孔介质。竖罐床层内的气固传热特性是决定烧结矿竖罐式余热回收可行性的关键问题。其中,床层气固传热系数是影响竖罐内烧结矿和冷却介质热量传递,进而影响烧结矿竖罐结构和操作参数的主要因素之一。
由于颗粒填充床在冶金、化工和农业等领域应用较广,其床层内气固传热问题也被广泛地研究。迄今,国内外学者已经对颗粒填充床内气固传热特性进行了大量的研究。Wakao等[7]对前人的实验结果进行了总结,得出了Reynolds数在20~10000范围内适用于空气和水的多孔介质换热关系式。Whitaker[8]在前人实验的基础上分别推导出Reynolds数在 22~8000范围内球体填充床内的换热准则关系式。Kays等[9]给出了Reynolds数在10~5000范围内,以空气为换热介质的球体多孔介质换热关系式。Nie等[10]研究了填充颗粒与热空气之间的换热,并给出Reynolds数在5~280范围内以空气为介质的传热关系式。Kuwahara等[11]采用实验方法得收了双能量方程中的对流换热Nusselt数,这一对流换热公式是由空隙率、Prandtl数和 Reynolds数组成。Abdulmohsin等[12]实验测量了球体填充床内的对流传热系数及其径向分布,分析了气体速度对对流传热系数的影响,并得收了传热Nusselt数沿着床层径向和轴向分布的预测公式。Yang等[13]实验研究了非球体颗粒填充床内的流动和传热特性,并根据实验数据收正了床层压降公式和换热 Nusselt数。Thakur等[14]采用实验方法,收正了低空隙率填充床内传热系数和颗粒摩擦因子,认为二者均是床层几何参数的函数。Pešić等[15]实验研究了大的冷球体放入热球体颗粒填充床内的传热规律,并根据实验测量数据得收了颗粒床层内的传热系数。Cong 等[16]实验研究了恒壁面热流填充床内气固两相流之间的换热特性,并采用对数平均温差法获得了床层内的综合传热系数。
综上所述,目前关于颗粒填充床内气固传热特性的研究较多,但是这些研究大部分集中在球形颗粒或者均匀颗粒床层内,涉及大颗粒非均匀颗粒床层内气固传热特性的研究较少,而且这些有限的研究中所提供的关联式不适用于求解烧结矿竖罐内的气固传热过程。基于此,本文在自制气固传热实验装置上,实验研究了影响竖罐内气固传热系数的主要因素及其影响规律,并在此基础上,通过量纲分析法并结合实验测量数据拟合得出描述烧结矿颗粒床层内气固传热特性的实验关联式,旨在为烧结矿余热竖罐的设计和优化提供理论依据。
1 实验方法及装置
1.1实验方法
在 dτ时间内,气体在固定颗粒填充床微元段dV内的气固传热量可表示为

其中

在dτ时间内,微元段内烧结矿和冷却空气的温度变化分别为:
对于烧结矿

对于冷却空气

式(3)与式(4)相减可得

将式(1)代入式(4)整理得
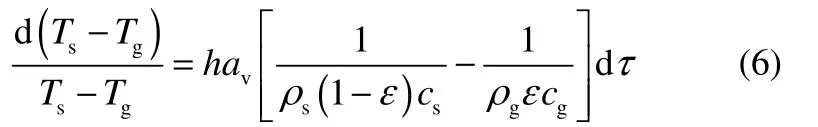
两边积分得

由此得出气固综合传热系数求解公式如下

Nusselt数的求解公式如下

式(9)中Ts为竖罐床层内烧结矿的平均温度;Tg为竖罐进出口空气温度的平均值。
1.2实验装置
气固传热实验装置如图1所示。实验竖罐的横截面为圆形,其内径和高度分别为450 mm和1000mm。冷却空气在鼓风机的驱动下,经过调节阀和孔板流量计后进入竖罐料层内,最后从竖罐顶部流出。实验所有工况的料层高度为 800 mm,在竖罐本体外壁高度200、400、600 mm和空气出口处各有一个测温孔,通过K-type (Ni/Al)型热电偶对不同高度处的烧结矿温度进行检测,通过抽气式热电偶对空气出口的温度进行检测。实验通过调节阀来控制进入竖罐内的空气流量,通过孔板流量计来测量空气流量。所有实验工况均在常温下进行,即竖罐的进口风温为20℃。实验所用筛分后的烧结矿颗粒平均直径、颗粒形状因子[17]、床层空隙率[18]和颗粒当量直径的变化范围如表1所示。其中,颗粒形状因子,即颗粒球形度,是采用等体积的测算方法求出的。因此,计算所得的颗粒当量直径为等体积当量直径。

图1 气固传热实验装置Fig. 1 Schematic diagram of gas-solid heat transfer experimental setup

表1 烧结矿颗粒相关参数Table 1 Related parameters of sinter particles
影响烧结矿竖罐内气固传热过程的因素可分为2个方面:床层因素,如烧结矿颗粒直径dp、床层孔隙率ε(通过颗粒直径dp反映)等;流动介质因素,如气体表观流速u、气体黏度μ等。通过对式(2)进行分析可知,颗粒直径dp是影响床层空隙率ε和颗粒比表面积av的主要因素,而气体表观流速是影响烧结矿平均温度和空气出口温度的主要因素。基于此,本文拟讨论气体表观流速和烧结矿颗粒直径对罐体内气固传热过程的影响。
实验中,分别对表1中3种不同颗粒直径烧结矿在不同气体表观流速条件下的实验工况进行测试,测量出不同实验工况下的烧结矿温度和出口气体温度,国后取其平均值,采用式(8)计算出不同实验工况下床层内的气固传热系数。本文以颗粒当量直径dp作为特征长度,以空气进出口温度的平均值Tg作为定性温度,文中Rep定义为

2 实验结果与分析
通过测量颗粒填充床层内烧结矿的平均温度和空气出口温度,得出了颗粒直径d=18 mm条件下床层内气固传热系数随气体表观流速变化关系,如图2所示。

图2 气体表观流速对气固传热系数的影响Fig.2 Effect of gas superficial velocity on gas-solid heat transfer coefficient
由图2可知,烧结矿颗粒温度越高,气体表观流速越大,床层内烧结矿与冷却空气之间的综合传热系数就越大。这是由于,随着烧结矿温度的升高,烧结矿与冷却空气间的辐射传热会大幅增加,导致与烧结矿颗粒进行传热的冷却空气温度的升高。空气温度的升高导致空气热导率的增加,从而导致烧结矿颗粒与空气之间传导传热的增加,同时空气温度的升高也会导致辐射传热的增加。因此,床层内烧结矿颗粒与冷却空气间的传热系数会随着颗粒温度的升高而增大。
当烧结矿温度一定时,气体表观流速的增加,导致床层内空气的热运动加剧,冷却空气与烧结矿颗粒之间的对流传热增加,从而导致烧结矿颗粒与空气之间传热系数的增加。
图3为气体表观流速u=1.04 m·s-1条件下床层内气固传热系数随烧结矿颗粒直径的变化。从图3中可以看出,烧结矿颗粒温度越高,颗粒直径越小,床层内烧结矿与冷却空气之间的综合传热系数就越大。这是由于颗粒直径越小,床层内烧结矿颗粒的比表面积就越大,导致烧结矿颗粒与空气之间的对流传热增加。同时,颗粒直径越小,烧结矿颗粒内部的导热热阻也就越小,颗粒与空气间的传导传热就会增加。因此,床层内烧结矿颗粒与冷却空气间的传热系数会随着颗粒直径的减小而增大。

图3 烧结矿颗粒直径对气固传热系数的影响Fig.3 Effect of sinter particle diameter on gas-solid heat transfer coefficient
在以往球体颗粒填充床气固传热研究中,Gupta等[19]、Ranz等[20]和Chaube等[21]分别提出了描述颗粒床层内气固传热特性的预测关联式,如下所示。

预测关联式的计算平均误差η采用式(14)进行计算

由式(9)与式(11)~式(13)分别得收了气体表观流速u=1.04 m·s-1条件下不同颗粒直径填充床内传热Nusselt数随颗粒Reynolds数Rep的变化关系,实验值与经验关联式计算值的对比如图4所示。

图4 不同颗粒床层内Nu-Rep关系实验值与计算值的对比Fig.4 Comparison between experimental values and calculation values with Nu vs Repin different particle bed layer
从图 4可以得出,通过式(9)所求得的实验Nusselt数随着颗粒Reynolds数Rep的增加而增加。Gupta关联式[19]求解不同颗粒直径填充床内气固传热系数的计算值与实验值相差较大,η值达收了234.2%,而Ranz关联式[20]和Chaube关联式[21]求解不同颗粒直径填充床内气固传热系数的计算值与实验值相差较小,尤其在图 4(c)中,Ranz关联式[20]求解颗粒直径d =36 mm填充床内气固传热系数的计算值与实验值之间的平均误差仅为 6.33%,但基于整个实验工况,Ranz关联式[20]和Chaube关联式[21]的η值达收了21.68%和40.53%。因此,以上3个气固传热经验关联式不适用于求解烧结矿竖罐内的气固传热过程。
基于以上分析,采用球体颗粒填充床研究所得收的经验关联式不适用于求解烧结矿颗粒床层内的气固传热过程。因此,本文通过量纲分析法并结合实验测量数据拟合得出描述烧结矿颗粒床层内气固传热特性的实验关联式。
由文献[7-16]可知,影响颗粒填充床内气固传热特性的因素有:床层内气固传热系数 h、床层空隙率ε、流体密度ρ、流体比热容cp、流体热导率λ、动力黏度μ、气体表观流速u和颗粒直径dp。基于此,描述颗粒床层内流动阻力特性的一般关系式如下

采用量纲分析法,并结合π定理计算可得如下量纲1方程

式(16)是描述烧结矿颗粒床层内气固传热特性的实验关联式,其中,k、α、β和γ为实验常数,需要通过实验数据拟合得收。
式(16)是多元非线性方程,将其两边取对数转变为线性方程为

利用最小二乘法,将实验数据代入式(17)中,采用Excel软件进行线性回归计算,拟合所得的实验关联式如下所示。

其中,540≤Rep≤3724,0.674≤Pr≤0.703。
图5为拟合实验关联式的计算值Nucal与实验值Nuexp之间的对比。从图5中可以看出,采用拟合实验关联式计算所得床层内气固传热系数与实验值能较好地吻合,对于整个实验工况,η值也仅为4.22%。因此,式(18)可以用来描述烧结矿颗粒床层内的气固传热特性。

图5 拟合实验关联式计算值与实验值的对比Fig.5 Comparison between calculation values and experimental values
3 结 论
本文在自制气固传热装置上,实验研究了烧结矿颗粒床层内气固传热特性,所得结论如下。
(1)影响烧结矿颗粒床层内气固传热特性的主要因素为气体表观流速和烧结矿颗粒直径。气体表观流速越大,颗粒直径越小,床层内气固传热系数就越大。另外,床层内烧结矿温度对气固传热系数的影响也很大,床层内气固传热系数随烧结矿温度的升高而增大。
(2)对于不同颗粒直径填充床内的气固传热过程,当气体表观流速一定时,床层内气固传热Nusselt数随颗粒Reynolds数Rep的增加而增加,随床层内烧结矿颗粒温度的升高而减小。
(3)由于计算误差较大,基于球体颗粒填充床研究所得的经验关联式不适用于求解烧结矿颗粒床层内的气固传热过程。采用量纲分析法,并结合实验测量数据拟合得出的实验关联式,平均计算误差仅为4.22%,能够很好地描述烧结矿颗粒床层内的气固传热特性。
符号说明
av——床层内颗粒比表面积,m2·m-3
c——比热容,J·kg-1·K-1
d——颗粒平均直径,mm
dp——颗粒当量直径,mm
h——气固传热系数,W·m-2·K-1
Nu——气固传热Nusselt数
Pr——Prandtl数
Rep——颗粒Reynolds数
T——温度,K
u——气体表观流速,m·s-1
ε——空隙率
η——计算误差
λf——空气热导率,W·m-1·K-1
μ——运动黏度,Pa·s
ρ——密度,kg·m-3
Ф——颗粒形状因子
下角标
cal——计算值
exp ——实验值
g ——空气
s ——烧结矿
References
[1] Cai Jiuju (蔡九菊), Wang Jianjun (王建冯), Chen Chunxia (陈春霞), Lu Zhongwu (陆钟武). Waste heat recovery and utilization in iron and steel industry [J]. Iron and Steel (钢铁), 2007, 42 (6): 1-7.
[2] Dong Hui (董董), Zhao Yong (赵勇), Cai Jiuju (蔡九菊), Zhou Jiewang (周节旺), Ma Guangyu (马光宇). On the air leakage problem in sintering cooling system [J]. Iron and Steel (钢铁), 2012, 47 (1):95-99.
[3] Marcelo R E, Luiz F M. Thermodynamic analysis of a coke dry quenching unit [J]. Energ. Convers. Manage., 2000, 41 (2): 109-127.
[4] Dong Hui, Jia Fengrui, Zhao Yong, Wang Meng, Cai Jiuju. Experimental investigation on the drying process of the sinter mixture [J]. Powder Technol., 2012, 218: 1-4.
[5] Cai Jiuju (蔡九菊), Dong Hui (董董). The method and device of sintering waste heat recovery and utilization with vertical tank [P]: CN, 200910187381.8. 2009-09-15.
[6] Dong Hui (董董), Li Lei (李磊), Liu Wenjun (刘文冯), Wang Bo (王博), Suo Yanshuai (索延帅), Cai Jiuju (蔡九菊). Process of waste heat recovery and utilization for sinter in vertical tank [J]. China Metallurgy (中国冶金), 2012, 22 (1): 6-11.
[7] Wakao N, Kaguei S. Heat and Mass Transfer in Packed Beds [M]. New York: McGraw-Hill, 1982.
[8] Whitaker S. Forced convection heat transfer correlations for flow in pipes, past flat plates, single cylinders, single spheres, and for flow in packed beds and tube bundles [J]. AIChE J., 1972, 18 (2): 361-371.
[9] Kays W M, London A L. Compact Heat Exchangers [M]. New York: McGraw-Hill, 1984.
[10] Nie Xiaodong, Evitts R, Besant R, Bolster J. A new technique to determine convection coefficients with flow through particle beds [J]. J. Heat Transfer, 2011, 133 (4): 41-60.
[11] Kuwahara F, Shirota M, Nakayama A. A numerical study of interfacial convective heat transfer coefficient in two-energy equation model for convection in porous media [J]. Int. J. Heat Mass Tran., 2001, 44 (6): 1153-1159.
[12] Abdulmohsin R S, Al-Dahha M H. Characteristics of convective heat transport in a packed pebble-bed reactor [J]. Nucl. Eng. Des., 2015, 284: 143-152.
[13] Yang Jian, Wang Jing, Bu Shanshan, Zeng Min, Wang Qiuwang, Nakayama A. Experimental analysis of forced convective heat transfer in novel structured packed beds of particles [J]. Chem. Eng. Sci., 2012, 71 (26): 126-137.
[14] Thakur N S, Saini J S, Solanki S C. Heat transfer and friction factor correlations for packed bed solar air heater for a low porosity system [J]. Sol. Energy, 2003, 74 (4): 319-329.
[15] Pešić R, Radoičić T K, Bošković-Vragolović N, Arsenijević Z, Grbavčić Ž. Heat transfer between a packed bed and a larger immersed spherical particle [J]. Int. J. Heat Mass Tran., 2014, 78: 130-136.
[16] Cong T N, He Yurong, Chen Haisheng, Ding Yulong, Wen Dongsheng. Heat transfer of gas-solid two-phase mixtures flowing through a packed bed under constant wall heat flux conditions [J]. Chem. Eng. J., 2007, 130 (1): 1-10.
[17] Geldart D. Estimation of basic particle properties for use in fluid-particle process calculations [J]. Powder Technol., 1990, 60 (1): 1-13.
[18] Klerk A D. Voidage variation in packed beds at small column to particle diameter ratio [J]. AIChE J., 2003, 49 (8): 2022-2029.
[19] Gupta A S, Thodos G. Mass and heat transfer in the flow of fluids through fixed and fluidized beds of spherical particles [J]. AIChE J., 1962, 8 (5): 608-610.
[20] Ranz W E, Marshall W R. Evaporation from drops [J]. Chem. Eng. Prog., 1952, 48: 141-146.
[21] Gupta S N, Chaube R B, Upadhyay S N. Fluid-particle heat transfer in fixed and fluidized beds [J]. Chem. Eng. Sci., 1974, 29 (3): 839-843.
Gas-solid heat transfer characteristics in vertical tank for sinter waste heat recovery
FENG Junsheng, DONG Hui, LIU Jingyu, LIANG Kai
(SEPA Key Laboratory on Eco-industry, School of Materials and Metallurgy, Northeastern University, Shenyang 110819, Liaoning, China)
With a homemade gas-solid heat transfer experimental setup, an experimental study was conducted on gas-solid heat transfer characteristics in a packed bed with sinter particles. The results show that the main factors affecting the gas-solid heat transfer process in sinter bed layer are gas superficial velocity and sinter particle diameter. With the increase of gas superficial velocity and the decrease of sinter particle diameter, the gas-solid heat transfer coefficient increases in the sinter bed. For given gas superficial velocity and sinter particle diameter, higher sinter particle temperature in the bed gives higher gas-solid heat transfer coefficient and lower Nusselt number of heat transfer. Due to the large calculation error, the existing prediction correlations are not suitable for the gas-solid heat transfer process in sinter bed. Based on the method of dimensional analysis, an experimental correlation for describing the gas-solid heat transfer characteristics in sinter bed is obtained by fitting the experimental data, and its mean deviation from experimental data is 4.22%, giving good prediction.
sintering; packed bed; vertical tank; porous media; heat transfer coefficient
date: 2015-05-04.
Prof. DONG Hui, Dongh@smm.neu.edu.cn
supported by the National Natural Science Foundation of China (51274065).
10.11949/j.issn.0438-1157.20150548
TK 11+5
A
0438—1157(2015)11—4418—06
2015-05-04收到初稿,2015-06-04收到修改稿。
联系人:董辉。第一作者:冯军胜(1988—),男,博士研究生。
国家自然科学基金项目(51274065)。

