求根MUSIC初值设置和更新算法

闫锋刚，张 薇，金 铭

(哈尔滨工业大学(威海)信息与电气工程学院，264209山东威海)

信号波达方向(direction-of-arrival，DOA)估计［1-2］是雷达、声呐、无线通信和无源定位等应用中经常遇到的重要研究课题.以多重信号分类(multiple signal classification，MUSIC)［3］和旋转不变子空间(estimate signal parameters via rotational invariance technique，ESPRIT)［4］为代表的子空间类算法的提出，实现了传统空间谱估计向超分辨测角的飞跃，但 MUSIC算法庞大的计算量和ESPRIT算法较低的估计精度阻碍了超分辨算法的工程化进度［5］.

在均匀线阵(uniform linear array，ULA)下，阵列导向矢量具有特殊的范德蒙结构，使得MUSIC算法繁杂的谱峰搜索简化为多项式求根问题，由此促成了求根 MUSIC(root-MUSIC)算法［5］的诞生.虽然 root-MUSIC仅是 MUSIC在ULA下的特例，然而理论分析和实验结果证明:root-MUSIC的估计精度比MUSIC的估计精度更高［6-7］，因而其相比于MUSIC实现了低复杂度和高精度的双赢.文献［8］通过理论分析论述了root-MUSIC估计性能与环境、阵元参数的内在联系;文献［9］借助中心对称阵列结构实现了root-MUSIC的实值化，在降低计算量的同时提高了算法的估计精度;文献［10-11］借助流型分离(manifold separation technique，MST)技术，将任意阵列的导向矢量近似地分裂成两个独立部分的乘积，利用包含信号角度信息且具有范德蒙结构的部分、以多项式求根实现信号 DOA估计.文献［12］利用任意阵列结构下的MUSIC空间谱是关于信号DOA周期函数的事实，提出了傅里叶域求根MUSIC(fourier-domain，FD-MUSIC)算法，将root-MUSIC由ULA推广到了任意阵列结构.文献［13］基于傅里叶级数的劳伦结构，对 FD-root-MUSIC进一步进行了改进，有效降低了多项式的求根阶数，降低了算法的复杂度.

上述算法丰富了root-MUSIC的理论内涵，但它们在实际工程应用中一般均需借助迭代算法对多项式求根.选择合适的初值并基于一定的原则对其更新和控制以使迭代快速、准确地收敛具有重要研究意义.

本文在分析root-MUSIC多项式根分布特点的基础上，提出了一种迭代初值到单位圆平均距离最短(least average distance to unit circle，LADTUC)的准则，进而基于该准则发展了一种适用于root-MUSIC的初值设置和更新算法.理论分析和试验结果表明，该算法能有效避免迭代过程中的错误解并加速迭代收敛速度，从而为root-MUSIC的实际工程化提供理论参考.

1 数据模型及root-MUSIC算法原理

1.1 数据模型

考察xoy平面上由M个以半波长间隔放置的阵元组成的ULA，假设阵列各通道附加高斯白噪声且空间有L个辐射源，定义波达方向DOA为信号来向与阵列法线的夹角，则阵列一次快拍接收数据为［3］

式中:x(t)是M×1维接收数据向量;s(t)是L×1

维信号向量;n(t)是M×1维噪声向量.A(θ)是M×L维导向矢量矩阵且导向矢量a(θ)定义为

阵列接收数据协方差矩阵定义为

式中:RS为信号协方差矩阵，σ2n为噪声功率.对R进行特征值分解，可得

式中:ρi，i=1，2，…，L和ρj，j=L+1，…，M分别为R的L个大特征值及(M-L)个小特征值，ei和ej分别为是ρi和ρj对应的特征矢量.定义:

则S和G的列分别张成信号子空间和噪声子空间.

1.2 root-MUSIC算法原理

依据上述阵列和数据模型，root-MUSIC算法定义如下所示的多项式［5］:

其中p(z)定义为

对f(z)求根即可获得DOA.由于f(z)存在z*项，求根较为复杂.为便于计算，做如下修正:

此时，多项式f(z)的阶数为2(M-1)，所以有(M-1)对根，每一对根是相互共轭的关系.这些根中的L个根z1，z2，…，zL正好分布在单位圆上，且

实际中，得到多项式f(z)中L个接近于单位圆的根后，可按下式求解信号DOA:

2 LADTUC准则及最佳初值设置

2.1 f(z)最小值设置

通常为得到DOA，只需根据式(8)令f(z)=0并求根即可，但当快拍数或信噪比较低时，在信号入射方向有

因此，为得到精确DOA，需估计fmin并对修正多项式f(z)-fmin=0进行求根.

由MUSIC零谱统计性能知，发射能量为Ei(i=1，2，…，L)的辐射源，在 MUSIC 空间零谱上产生的最小值为［14-15］

式中J为快拍数，辐射源能量Ei(i=1，2，…，L)在一般情况下是难以获得的，一种近似的求解方法是认为每个辐射源的辐射能量都相同，即

式中:E为观测信号总能量，ρj是协方差矩阵R特征值分解后对应的噪声空间特征值，其数值等于噪声的能量.由上述分析，可设置

实际中，当快拍数或信噪比较高时，fmin接近于0.此时，可直接选取近似值fmin≈0.

2.2 最佳迭代初值设置

对方程f(z)-fmin=0采用牛顿法求解［16］，得

式中:f'(z)为f(z)的一阶导函数，z0为迭代初值，zn是经过第n次迭代后得到的解.

可选取一定容差ϑ，当z0与zn满足

时迭代结束，然后将zn带入式(11)即可求得DOA.

迭代初值z0的选取至关重要，其直接决定着迭代的收敛速度和正确性.由于代表信号DOA的根分布在单位圆上，故z0的选择应以到单位圆平均距离最短为准则，这便是本文提出的LADTUC准则，后续仿真实验证实了该准则的合理性.

由于DOA取值范围为［-π/2，π/2］，只需考虑半单位圆即可.为了叙述便利，以下均用U代表上半单位圆弧.设R(cosθ，sinθ)为U上任意一点，其中，θ为R与圆心连线的倾角，显然，θ符合均匀分布特性，其概率密度函数为

设最佳迭代初值为Q1，则Q1到R(cosθ，sinθ)平均距离的平方L21为

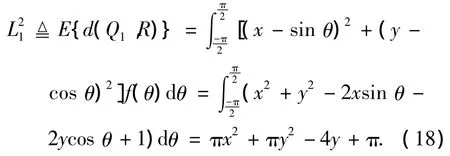
依据LADTUC原则，令

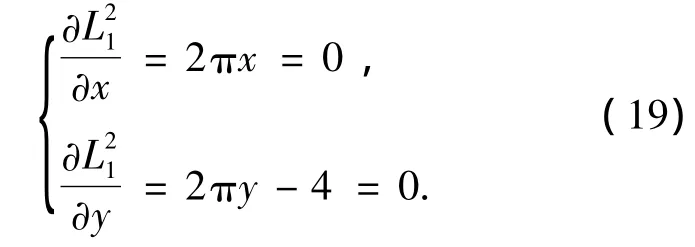
易求得，最佳迭代初值为

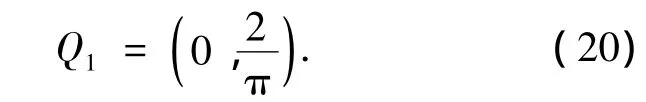
2.3 迭代初值更新方法

LADTUC原则保证的是平均意义下的最佳，实际中的某次迭代解算可能因受到U内、外根的干扰而无法收敛到U上.为了解决该问题，定义数列Qn:

式中:点A为弧Un，n=1，2，…上任意一点，Un为将U进行k1倍等分后、顺时针方向的第k2+1份弧.易求得k1、k2与n满足如下关系:

式中符号「·⏋表示向上取整.

由式(21)可见:Qn，n=1，2，… 是 LADTUC意义下对Q1的扩展，其代表的是到弧Un平均距离最小的点列.设弧Un上、下端点和圆心连线的倾角为θ1和θ2，易求得

利用类似于式(18)、(19)的方法，可得Qn，n=1，2，… 的横、纵坐标值为

显然，当n→ ∞ 时，θ1→θ2→0，Qn→1.因此，Qn的所有元素均在U内.图1给出了Qn的前7个元素在U内的相对位置关系.基于Qn，可对迭代初值更新，以保证迭代最终收敛于U上.

图1 数列Q的前7个元素

假设U上分布正确根R1和R2，U内、外分别分布干扰根Ⅰ1、Ⅰ2和O1、O2，如图 2 所示.依据LADTUC原则，首先设置迭代初值z0为Q1，若迭代收敛于干扰根Ⅰ1，则更新z0为Ⅰ1相对于Q1反方向的Q2，以避免Ⅰ1的干扰;否则，更新z0为Q3.若更新后迭代仍收敛于干扰根Ⅰ2，则更新z0为Ⅰ2相对于Q3反方向的Q5，以避免Ⅰ2的干扰;同理，当迭代再次收敛于干扰根O1时，则更新z0为O1相对于Q5反方向的Q4，以避免O1的干扰，….如此反复更新z0，直至迭代收敛于正确根R1.

在LADTUC原则下，每次初值更新都是以平均最接近U的等分弧段而进行.为防止多次更新仍不收敛，可预设最大容忍迭代次数N，当迭代次数达到N/2时，下一步则应“逃逸”至相反的半弧进行.如图2所示，当设置z0为Q4仍不收敛时，下一步应更新z0为Q3，以在U的右半弧寻求正确根R2.

图2 LADTUC原则下迭代初值设置和更新

3 收敛性能分析

式(8)根的总数为

其中，代表辐射源DOA的根有L对，因此，干扰根的个数为

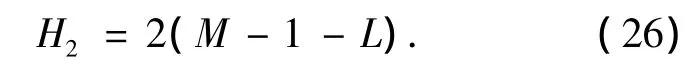
采用LATDUC原则进行迭代初值设置和更新时，当干扰根距离数列Q第k个元素Qk的距离小于Qk到Uk的平均距离时，则迭代会收敛到干扰根而不会收敛到单位圆上，此时收敛会失败.因而，第k次初值设置收敛失败的概率为

因此，经过k次初值更新，成功收敛概率为

由于0＜qk＜1，由式(28)可见:pLADTUC随k的增加急剧增大，因而本文算法每经一次初值更新后，成功收敛的概率都会大幅增加.

若采用随机法设置迭代初值，只进行1次初值设置迭代收敛成功(收敛到U上)的概率为

由于随机法的每次初值设置相互独立，故其经过k次初值设置成功收敛的概率恒为prand，这意味着随机设置和更新初值的收敛概率并不会随k的增加而增大.因而，LADTUC相比于随机设置、更新迭代初值法从统计平均上提高了成功收敛的概率.

4 仿真试验

试验采用ULA阵列，阵元间距为半个波长.设快拍数J=256，迭代停止容差ϑ=10-2，最大容忍迭代次数N=30.设辐射能量彼此相等，信源DOA通过随机生成［-π/2，π/2］上均匀分布的L个角度得到.Monte Carlo试验次数均为500次.

4.1 最佳迭代初值Q1合理性验证

本试验用于验证式(20)给出最佳迭代初值Q1(0，2/π)的合理性.试验设置阵元数M=10，迭代初值为z0=0+Δi，其中步长以间隔0.05从0.05增大到1.试验分为如下两个部分.

首先，选取L=3并以RSN为参变量，统计Δ的取值与采用牛顿法求解方程根的迭代次数及收敛概率的关系，结果如图3所示.试验中，当迭代总次数超过N=30时认为收敛失败.

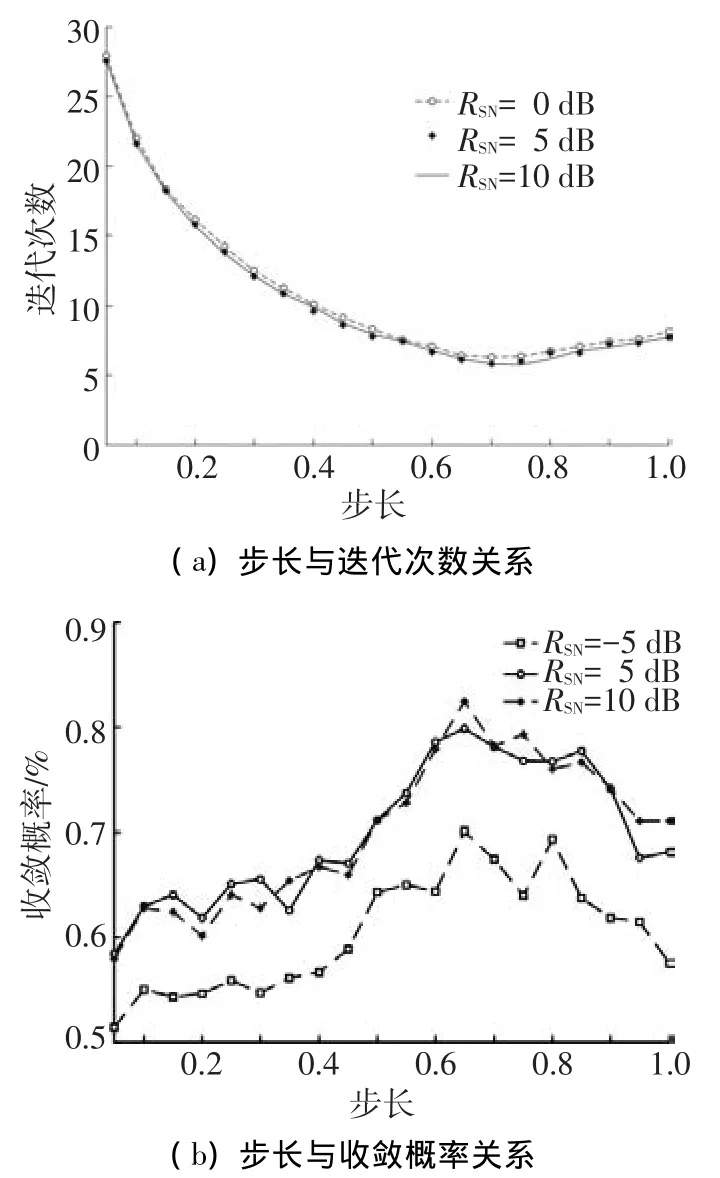
图3 信噪比参变时，步长与迭代次数及收敛概率关系

其次，选取RSN=5 dB并以信号数L为参变量，统计步长值与采用牛顿法求解方程根的迭代次数及收敛概率的关系，结果见图4.试验中，当迭代总次数超过N=30时则认为收敛失败.

由图3、4可见:相比于RSN，L对迭代次数和迭代的成功收敛概率影响更强，这是由于RSN仅影响方程(8)根的分布，而L除了影响方程根分布之外还决定着干扰根的多少.另外，由图3、4可观察到:当Δ=0.65≈2/π时，成功收敛概率最大，迭代次数也接近最小，这证明了初值Q1(0，2/π)的合理性.

4.2 LADTUC初值更新原则的合理性验证

本试验用于验证图2所示的基于LADTUC原则进行迭代初值更新方法的合理性.试验设置阵元数M=15，RSN=5 dB，然后分别按LADUC原则和随机法更新迭代初值，并按如下两方面进行平均结果统计.

首先，统计迭代初值更新次数与信号数L的关系，结果见图5.试验中，当迭代总次数超过N=30时则认为收敛失败.

图4 信号数参变时，步长与迭代次数及收敛概率关系

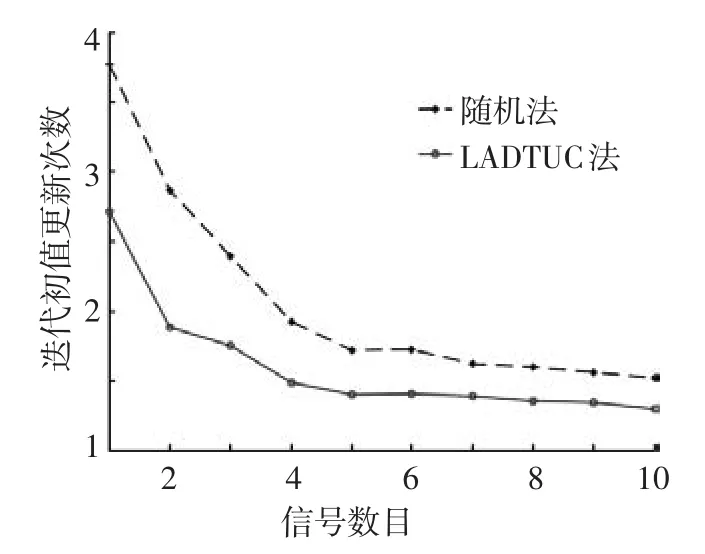
图5 迭代初值更新次数与信号数目关系

其次，设置初值更新的最大容忍次数为3，然后统计迭代成功收敛概率与信号数L的关系，结果见图6.试验中，当迭代总次数超过N=30或初值更新次数超过3次时，均认为收敛失败.

由图5可见:基于LADTUC原则进行迭代初值更新，最多只需要进行3次以下的更新即可成功收敛，其相比于随机更新法显著减少了更新次数.另一方面，当信号数L较小时，本文方法所需的更新次数比随机法的更新次数更少.这是因为L越小时方程(8)的干扰根较多，而LADTUC原则相比于随机法从平均意义上保证了迭代收敛概率更高，因此其所需的初值更新次数越少.

由图6可见，当L＞2时，LADTUC原则下的迭代成功收敛概率均＞95%;而随机法的成功收敛概率仅为85%左右，其相比于本文方法低10个百分点.与图5相似，从图6可见:本文方法相比于随机发在信号数L较少(即式(8)干扰根较多)时的优势更为明显，迭代收敛概率更高.上述实验结果说明了依据LADTUC准则对root-MUSIC算法进行初值设置和更新是合理性的.

图6 迭代成功收敛概率与信号数目关系

5 结语

本文在分析root-MUSIC算法根分布特点的基础上，提出了一种利用工程实现的root-MUSIC初值设置和更新算法.该算法充分利用了LADTUC原则对于迭代收敛的控制作用，保证了root-MUSIC算法迭代收敛的快速性和正确性，为root-MUSIC算法的实际工程化提供了一定的理论参考.

［1］JIN H.Joint space-time parameter estimation for multicarrier CDMA systems ［J］.IEEE Transactions on Vehicular Technology，2012，61(7):3306-3311.

［2］KHABBAZIBASMENJ A.Efficient transmit beamspace design for search-free based DOA estimation in MIMO radar［J］.IEEE Transactions on Signal Processing，2014，62，(6):1490-1500.

［3］YAN F G，JIN M，LIU S，et al.Real-valued MUSIC for efficient direction estimation with arbitrary array geometries ［J］. IEEE Transactions on Signal Processing，2014，62(6):1548-1560.

［4］ZHENG G M，CAO B X，YANG M L.Unitary ESPRIT algorithm for bistatic MIMO radar［J］.Electronics Letters，2012，48(3):1122-1123.

［5］CHENG Q，HUANG L，So H C.Improved unitary root-MUSIC for DOA estimation based on pseudo-noise resampling［J］.IEEE Signal Processing Letters，2014，21(2):140-144.

［6］STOCIA P，NEHORAI A.MUSIC，maximum likelihood，and Cramer-Rao bound:further results and comparisons［J］.IEEE Transactions on Acoustics，Speech and Signal Processing，1990，38(12):2140-2150.

［7］CAO Y，ZHANG Z，DAI F，et al.Direction of arrival estimation for monostatic multiple-input multiple-output radar with arbitrary array structures ［J］.IET Radar，Sonar＆ Navigation，2012，6(7):679-686.

［8］LI F，LIU H，VACCARO R J.Performance analysis for DOA estimation algorithms:Unification，Simplification，and Observations［J］.IEEE Transactions on Aerospace and Electronic Systems，1993，29(4):1170-1184.

［9］MARIUS P，ALEX B G，MARTIN H.Unitary root-MUSIC with a real-valued eigendecomposition:a theoretical and experimental performance study［J］.IEEE Transactions on Signal Processing，2000，48(5):1306-1314.

［10］BELLONI F，RICHTER A，KOIVUNEN V.Extension of root-MUSIC to non-ULA array configurations［C］//International Conference on Acoustics，Speech and Signal Processing(ICASSP).Toulouse，France:IEEE，2006:4(5):14-19.

［11］BELLONI F，RICHTER A，KOIVUNEN V.DOA estimation via manifold separation for arbitrary array structures ［J］. IEEE Transactions on Signal Processing，2007，55(10):4800-4810.

［12］RUBSAMEN M，GERSHMAN A B.Direction-of-arrival estimation for non-uniform sensor arrays:from manifold separation to Fourier domain MUSIC methods［J］.IEEE Transactions on Signal Processing，2009，57(2):588-599.

［13］ZHUANG J，LI W，MANIKAS A.Fast root-MUSIC for arbitrary arrays ［J］.Electronics Letters，2010，46(2):174-176.

［14］HARRY B，MICHAEL L，WENGROVITZ S.Statistical characterization of the MUSIC null spectrum［J］.IEEE Transactions on Signal Processing，1991，39(6):1911-1921.

［15］BARABELL A J.Improving the resolution performance ofeigenstructure based direction finding algorithms［C］//International Conference on Acoustics，Speech and Signal Processing(ICASSP).Boston，America:IEEE，1983:336-339.

［16］CADZOW J A.Multiple source location-the signal subspace approach ［J］. IEEE Transactions on Acoustics， Speech and SignalProcessing， 1990，38(7):1110-1125.