多口径组合阵列子空间DOA测向算法

果 然，毛兴鹏，李绍滨

(哈尔滨工业大学电子与信息工程学院，150001哈尔滨)

信号测向技术近几十年来受到国内外学者关注，一系列重要算法被提出，包括DBF类经典算法、MUSIC［1］类信号子空间算法、ESPRIT［2］算法和最大似然算法［3-4］，以及很多衍生算法［5-9］.其中MUSIC算法由于具备较高测向精度［9-11］、适中的运算量以及性能不受阵列波束宽度影响，可适用于各种阵列形式等特点，成为众多学者和技术人员研究的焦点.

虽然MUSIC算法可以应用于各种阵列，但是不理想的阵列形式会带来严重的阵列模糊，导致空间谱中出现伪峰进而影响DOA(direction of arrival)估计性能.理论上可证明，均匀线阵(Uniform linear array，ULA)中阵元的间距不得超过半波长，否则会出现阵列模糊［12］.对非均匀线阵和阵元数较少的均匀圆阵(uniform circular array，UCA)，当阵列尺寸较大时，也会由于类似的原因在空间谱中形成伪峰，影响对真实信号方向的辨别.文献［13］中基于微分几何思想，提出一种检验阵列模糊方法，但是无法消除阵列模糊.对于阵元间距小于等于半波长的线阵和圆阵，虽然阵列模糊现象得以避免，要得到较高的测向精度及分辨力性能，需要较大的阵列口径，从而需要大量阵元，导致系统成本和复杂度大大提高.基于波束形成准则进行优化得到稀布阵［14-18］是一种有效降低阵列阵元数目的方法，文献［19-21］对稀布阵的去阵列模糊进行研究，在二维平面阵情况下，仍然需要较多的阵元组阵.

针对上述问题，本文提出一种基于不同口径的阵列组合成的组合阵列进行DOA估计方法.该方法既可以解决阵列模糊问题，又具有较好的算法精度和分辨力性能，同时所需要的阵元数目较少，与传统的MUSIC算法相比能有效降低系统复杂度和算法运算量.本文在给出该算法基本原理基础上，通过理论分析和计算机仿真系统研究该算法的精度和分辨力等性能，并与稀布阵等现代DOA估计方法进行对比.

1 基础理论

1.1 经典模型与MUSIC算法的基本原理

考虑一个M个阵元组成的阵列，N个不完全相干的与阵列处于同一平面的窄带信号从不同方向到达阵列，如图1所示.

图1 信号入射模型

第i个阵元的输出为

式中:sk(t)为第k个信号，ni(t)为加性高斯白噪声，ω0为N个窄带信号的中心频率;参数τki为相对基准阵元第k个信号到达第i个阵元的时延，其形式取决于信号的到达角度和阵列的形式.对ULA来说，τki为(i-1)dsinθk/c，θk为第k个信号的方位角，d为阵元间距，c为光速;对于由M个阵元组成的 UCA，τki=rcos(φk-2πi/M)sinθk/c，φk与θk分别为第k个信号的方位角和俯仰角，r为UCA的半径.对于一个任意平面阵列，τki=((xicosφk+yisinφk)sinθk)/c，xi与yi为第i个阵元的位置.用向量的形式输入信号为X(t)=［x1(t)，…，xM(t)］T.则经数字采样后的输入信号为

X(t)协方差矩阵为

式中:ⅠM为M阶单位阵;λi代表Rx特征值，且有

为加性高斯噪声方差;ui为对应λi特征值向量.在二维阵列MUSIC算法中，定义空间谱为

这里‖·‖代表向量的欧几里得范数，UN=(uN+1，uN+2，…，uM)为噪声子空间矩阵.向量a为导向矢量，其形式与矩阵A中的列向量相似.a中的每个元素为方位角的函数，这样空间谱P可看做方位角和俯仰角的函数P(φ，θ).计算空间谱值，其中N个峰值的位置即为到达信号方位的估计值.

1.2 二维阵列模糊

文献［12］给出:对ULA阵列，当阵元间距小于等于半波长时可得秩N-1的抗模糊特性(即目标个数少于N-1的信号，都不会造成阵列模糊).但对于UCA，阵列模糊的论证变得很复杂.文献给出关于UCA不充分的一些结论，但并不能排除圆阵的最差特性.文献［13］给出利用高维微分几何方法对线阵的均匀剖分模糊性的分析，可扩展到圆阵当中，不能排除其他类型的阵列模糊.为避免阵列模糊的出现，现有方法一般采用减小阵元间隔或者设计特殊阵列形式的方法.图2采用8阵元5倍波长半径的圆阵绘制的空间谱图，单一入射信号方向为方位角41.3°，俯仰角34°，能看到空间谱受到严重的阵列模糊影响，出现大量伪峰.

1.3 空间谱计算的运算复杂度

采用减小阵元间隔方法克服阵列模糊需要更多阵元，导致系统成本增加和复杂度提高，并加重运算负担.即使能找到一种可避免阵列模糊，而且只需少量阵元的大尺寸稀布阵列［22-23］，由于口径较大，也会导致空间谱中得到过分尖锐的峰，这也给谱峰搜索带来了困难.

图3(a)、(b)都是在采用半径为5倍波长的7阵元UCA，信噪比、快拍数相同，信号从方位角41°，俯仰角34°入射时得到的空间谱，图3(a)中，在方位角上对空间谱采用了1°的采样间隔，在图3(b)中采用了2°的采样间隔.在俯仰角上均采用了1°采样间隔.图3(a)获得清晰的谱峰，也避免阵列模糊现象，但是将采样间隔提高到2°之后，空间谱形状就变得较差，难以分辨出真实谱峰.其他大口径稀疏阵列也存在类似问题.即使成功设计出可避免阵列模糊现象的大尺寸稀布阵，也要对空间谱进相当行密集的采样计算才能得到良好的谱峰形状.这对实际系统的计算能力提出较高要求.

图3 不同采样率下空间谱对比

1.4 阵列口径与测向精度和分辨力关系

衡量DOA测向算法的两个重要指标是估计精度和对于空间临近信号的分辨力.文献［10］分析MUSIC算法的测向精度性能，文献［11］则给出MUSIC算法分辨力性能分析.研究表明，除信噪比、快拍数等因素外，测向精度和分辨力与阵列中阵元布置密切相关，更大的阵列口径和更多的阵元数目，都对算法性能有所帮助，而其中阵列的口径起着更为显著的作用.为避免阵列模糊而增加大量阵元，并不会像扩大阵列的口径那样显著提高算法性能，反而会导致算法复杂度大大提高.如果能够采用一种新的阵列，在较大的阵列口径内，使用较少的阵元就能够避免阵列模糊，就可在大幅提高系统性能的基础上避免系统复杂度和运算量的增加.

2 多孔径组合阵列测向算法

为利用较大口径实现更理想的测向精度和分辨力性能，同时避免阵列模糊和过分锐利的谱峰带来的较大空间谱计算复杂度，本文提出一种利用不同口径的阵列构成的组合阵进行测向的算法.

2.1 阵列形式

以口径不同的圆阵形成的组合阵列为例，内侧采用6阵元组成半径为半波长的均匀圆阵，外侧采用3阵元、半径为5倍波长的均匀圆阵，如图4所示.外侧大尺寸阵列可带来较高的测向精度和分辨力性能，而内侧小阵列的排布使算法可有效回避阵列模糊的影响，同时提供对较多信号的检测能力.

图4 组合阵的形式示意

但如果直接对此阵列采用MUSIC算法，由于阵列孔径较大，得到的空间谱峰仍然很锐利，给谱峰搜索带来困难.为解决这个问题，给出一种改进的空间谱表达式，并说明改进带来的益处.

2.2 改进的空间谱形式

对于式(4)中空间谱P(θ)表达式，可得另一种空间谱的形式为

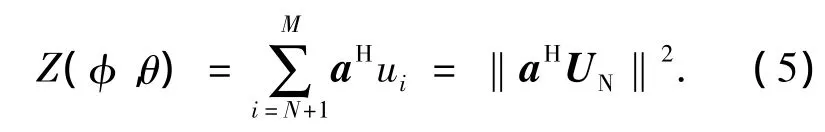
Z(φ，θ)为P(φ，θ)的倒数.在到达信号对应的位置，Z(φ，θ)值接近0.但由于噪声影响，在对应信号到达方向上，Z(φ，θ)有一定误差，在多于一个信号的情况下使P(φ，θ)对应峰值的高度有较大不同，相差达到5 dB甚至更多.在信噪比发生变化时，谱峰高度的变化也变得很剧烈.非常尖锐的谱峰以及不同的峰值高度，都对空间谱的计算和谱峰检测造成困难.因此给出一个新的空间谱表达形式

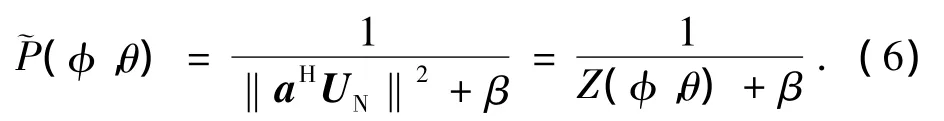
式中:β为一个很小的数值.易知(φ，θ)与P(φ，θ)有相近的形状，可利用(φ，θ)进行信号的方位估计.在Z(φ，θ)远小于β时，(φ，θ)≈1/β，因此在所有的信号方位上(φ，θ)都具有高度相近的谱峰.且在采取较小尺寸的阵列时，它使空间谱形状得以平滑.可利用小尺寸阵列，适当降低空间谱的采样率，估计出信号的大致方位之后，再利用外侧大尺寸稀疏阵列提供的较高精度和分辨力特性，对信号波达方向进行更为精确估计.

说明(φ，θ)可在多大程度上降低空间谱的采样间隔.假设采用图5所示组合阵列的内侧6阵元UCA，单信号到达角度为方位角φ0，俯仰角为90°.为简化推导，考虑方位角的采样.记(φ，90°)为(φ).由于低采样率的限制，假设最近的采样值为0.只要证明(0)与(φ0)的数值相差较小，说明该采样率能成功估计出目标到达方向的近似值.假设0＜φ0(当0＞φ0，分析方式相似)，有

式中(φ)为(φ)的导数.由式(6)可知

利用‖a0‖2=aH(φ)a(φ)=M.在单信号情况下，和a(φ)=将 内 侧 阵列的导向矢量代入，并考虑到M=6.

由式(10)、(11)得到在信号到达方位附近，有

代入式(8)可得

式中φ＜φ0.将式(13)代入式(8)可得

当取β=0.1时，当方位角上空间谱的计算步进扩大至4°，有|φ00|≥2°，可得(φ0)(0)≤3.607.而(θ0)≈10，谱峰高度下降不大.在MUSIC算法的谱峰检测当中，通常认为低于最高谱峰值5 dB之内的极值，都可认为该方向有信号到达.在谱峰最大值为10，谱峰高度下降大小＜4.43时，满足这个条件.因此当采样间隔不超过4°时，仅采用内测小阵列可以检测出所有谱峰.式(14)并没考虑分母变化的影响，而仿真表明，当方位角采样扩大到5°的时候也能得到可接受的空间谱.当俯仰角＜90°时，易知采样间隔仍然满足要求.对于俯仰角做基本相同的分析，得到相似的结论.用(φ，θ)形式的空间谱，可先用内侧阵列采用较大的采样间隔估计出信号的大致到达角度，再利用外侧阵列小范围搜索，从而降低计算复杂度.

2.3 算法说明和步骤

首先利用内侧小阵列计算空间谱得到信号到达角的大致位置，然后在信号到达角范围附近，利用外侧的大口径阵列进行更密集的空间谱计算，得到更精确的角度估计结果.

举例说明该算法的流程.假定空间中3个信号分别从方位角 25.35°、35.12°、213°，俯仰角40.21°、40.5°、71.2°入射.信噪比为 5 dB，快拍数100.

先利用内侧阵元计算式(6)所示空间谱，俯仰角和方位角采样间隔均为4°.得到图5(a)的空间谱(这里空间谱的高度采用绝对数值).根据该空间谱形状，可确定信号大致来向.取最大峰值的一半作为门限，认为超过门限的区域内可能有信号到达.由于内侧阵列本身分辨力的限制，有时并不能成功分辨出空间中邻近的信号，但只要能够成功得到信号的到达区域，就可利用外侧阵列更高的分辨率进行进一步的区分.能够看到两个谱峰高度值都在7附近，能够清晰检出.

在获得目标信号到达角的大致范围后，可加入外侧阵元的快拍进行更细致的搜索.为进一步节约运算量，可对外侧阵元的快拍进行＜1的加权，即将外侧阵元的增益降低，再与内侧阵元一起计算空间谱.这时得到较平滑的空间谱，可继续采用较大的采样间隔搜索谱峰位置.外侧阵元得到的数据降低到原始值的0.3倍，采样间隔为2°，在上一步确定的信号到达范围内，得到的空间谱图见图5(b).设定门限，进一步缩小信号可能的到达范围.

提高外侧阵列的增益，在上一步得到的信号到达角范围的基础上，缩小采样间隔.直接使用整个阵列的原始数据计算空间谱，采样间隔为1°.可见图5(c)得到相当锐利的谱峰.如果扫描步进已经达到所需精度，可对信号的方位进行估计.否则再次缩小范围和采样间隔，进行更精确的搜索.

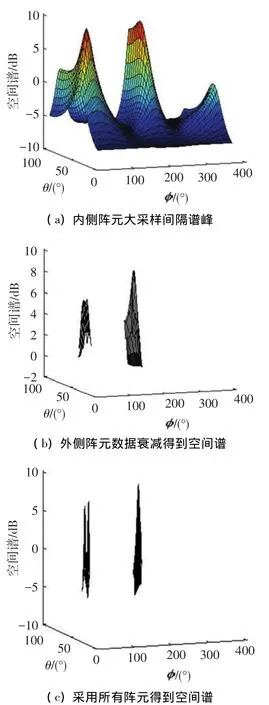
图5 算法中各个步骤生成的空间谱

算法步骤总结如下:

1)对阵列接收到的数据，只采用内侧阵列的数据计算式(6)中的空间谱，用较大的空间谱计算步进，确定波达信号的大致范围.

2)加入经过衰减的外侧阵列数据，减小空间谱计算步进，在上一步确定的信号到达范围内再次进行搜索.

3)直接采用所有阵元的原始数据，在第2步中确定计算空间谱中再次缩小范围进行搜索.如还没有达到精度要求，重复这一步，逐次减小计算步进，直到满足估计精度.

3 算法的精度、分辨力性能与复杂度分析

从理论分析基于组合阵列的新算法的精度和分辨力性能，且与其他3种稀布阵的性能进行对比.定量比较本算法和普通MUSIC算法的计算复杂度.

3.1 MUSIC算法和基于组合阵改进MUSIC算

法的精度性能分析

文献［10］给出了MUSIC算法的测向精度公式的一个重要结果.

式中:ωi为需要估计的参数，可看做信号的方位角φ或是俯仰角θ.i为参数的估计结果，K为阵列采样的快拍数

在多信号情形下，由于与信号子空间对应的特征值难以求出，难以利用该公式得到准确信号误差.但对于单信号和2个信号情况，特征值和特征向量有近似公式可计算，可定量分析误差大小.

在单信号情形下，式(15)变为

其中:

将式(17)～(19)代入式(16)化简为

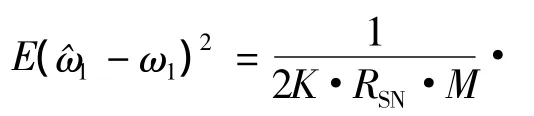
在2个信号的情形下:

式中i=1、2.将式(21)～(24)代入式(25)，可得到类似式(20)的表达结果.

若阵列形式已知，式(20)、(25)给出单信号和2个信号情形下，MUSIC算法的估计精度.

图6给出了测向误差的理论结果，仿真中使用快拍数为50.阵列1、2、3分别采用半径为3～5倍波长的9单元均匀圆阵，组合阵列的形式见图4和图6(a)为单个信号情形下，当信噪比变化时，不同半径的UCA阵列方位角测向误差曲线.信号入射方向为方位角15°，俯仰角60°.图6(b)为2个信号情形下，当信噪比变化时，不同半径UCA阵列的方位角测向误差曲线.2个信号入射方向的方位角分别为 15°和 137°，俯仰角均为 60°.

图6(a)、(b)看到，MUSIC算法的测向精度随阵列口径变大而提高，符合理论分析结果.而组合阵列测向性能接近阵列1和阵列2，略差于半径为5倍波长的阵列3.式(20)中，分母部分包含有阵列的阵元数N，可知阵元数对算法的精度性能也有一定的影响.而式(25)中系数，结合式(21)、(22)可知，阵列阵元数越多，λ1和λ2的数值越大，而测向误差的方差就越小.因此本文中对算法在精度性能方面并没有太大优势.但在信噪比＞5 dB时，组合阵列在单信号和多信号下都能得到方差在0.1°以下的方位角测向误差，可满足实际应用的需求.

图6 方位角测向误差理论计算结果

3.2 与MUSIC算法的分辨力性能对比

DOA算法的另一个重要指标是对空间到达方向邻近信号的分辨力性能.文献［10］中给出两个信号能够成功分辨的准则.仅分析方位角的分辨能力，俯仰角的分析完全类似.假设2个信号的到达方向方位角为φ1和φ2，俯仰角相同，推导省去.当P((φ1+φ2)/2)＜P(φ1)且P((φ1+φ2)/2)＜P(φ2)，即Z((φ1+φ2)/2)＞Z(φ1)且Z((φ1+φ2)/2)＞Z(φ2)时，2个邻近信号可分辨.为使分辨结果可靠，预留5 dB误差空间，即当式(26)、(27)两式成立时，邻近信号能成功分辨.

记φ0=(φ1+φ2)/2，a0=a(φ0).由零谱的定义知:

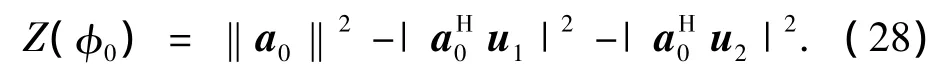
对文献［24］中的式(30)加以变换

式中i=1、2，

将式(28)～(30)代入式(26)、(27)，可得

将式(22)～(24)代入式(31)并将快拍数K移到左侧

得到对于某阵列，给定的信噪比和信号到达角时，需要多少快拍数才能成功区分信号到达角度.可据此来判断算法的性能，需要快拍数较少的算法无疑有更大的优越性.

图7给出采用不同阵列形式时分辨力性能对比.仿真中使用2个等功率的不相干信号，其入射方位角分别为 29.75°、32.76°，俯仰角均为 60°.由式(32)得到3种不同半径UCA和本文中提出的阵列与算法，成功分辨这2个信号所需的快拍数.能够看到本文采用的阵列分辨力性能相当于4倍波长半径的9阵元UCA.

图7 分辨力性能理论结果对比

3.3 算法精度性能分析

常规MUSIC算法与文中算法对单一空间谱值的运算量相差不多，因此计算复杂度大小取决于算法需要计算的空间谱点数.对于常规MUSIC算法，空间谱点数取决于对空间谱的采样步进，而空间谱的采样步进又取决于希望得到的算法精度.假设希望算法具备0.5°以内的误差，通常需要0.5°的采样步进.在方位角变化范围为0～360°，俯仰角变化方位为0～90°时，需要个空间谱点数.但是如果采用文中的方法，在当前阵列布局的情况下，第一次全局计算空间谱，可采用4°的大采样步进，考虑到整数除法因素，需要计算的空间谱点数为360/4×(90/4+1)≈2 160.后续步骤中搜索范围要远远小于全局搜索范围，需要的空间谱点数也远少于第一次计算出的点数，因此计算复杂度可能降低50倍以上.由于到达信号的个数可能不同，需要计算的点数也可能有变化.

4 仿真结果

进一步采用蒙特卡洛仿真来对比采用组合阵列和稀布阵时MUSIC算法性能.

目前还没有专门针对MUSIC算法提出并进行相应优化的稀布阵，因此将本文提出的算法与文献［15-17］中给出的3种稀布阵列运行MUSIC算法时的性能进行对比.文献［15-16］中的阵列均为为长、宽分别为5倍波长和2.5倍波长的矩形平面阵列，阵元数量为108，阵元摆放方式有所不同;文献［17］中为由43个阵元组成的稀疏同心圆阵列.

图8(a)、(b)给出单个信号情况下，本文提出的阵列与半径不同的9阵元UCA的测向误差对比，以及3种稀布阵的测向误差对比.仿真条件加性高斯白噪声，均采用50快拍数，单个信号从方位角 15.13°，俯仰角 60.52°入射.图中给出各种阵列形式下同时考虑俯仰角和方位角得到的测向误差标准差.图8(c)、(d)则是2个信号的情形，其他仿真条件与前相同，信号分别从方位角15.13°、30.75°入射，俯仰角 60.52°、60.31°入射.能看到，基于组合阵列的新算法虽然测向误差与3倍波长的圆阵基本一致，略差于其他阵列，但是仍然具备较好的测向精度性能.

图9(a)、(b)给出本文提出的阵列与半径不同的9阵元UCA的分辨力对比，以及3种稀布阵的分辨力对比.仿真条件加性高斯白噪声，50快拍数.2 个信号分别从方位角29.73°、32.76°入射，俯仰角60.52、60.31°入射.图中给出组合阵以及其他稀布阵成功分辨出这2个信号的概率.在分辨力性能上，本文提出的阵列要略低于5倍波长半径的UCA，与4倍波长UCA基本一致，相对其他的UCA阵列和稀布阵，新阵列都具有更高的分辨能力.

表1给出文中算法与常规MUSIC算法在不同的空间谱计算步进下需要的空间谱点数对比.这里方位角与俯仰角的变化范围均为0～90°与0～360°.文中算法第1步从4°搜索步进开始，每次搜索步进减半.由于不同阵列的阵元数有多种可能，仅统计空间谱的计算点数.表1中看到，MUSIC算法随着所需精度的提高，需要降低步进，使得计算点数快速增加.本文给出的算法，随着步进的降低计算点数仅有少量增加，使得计算量上升很小.因此在计算复杂度方面，本文算法有较大优势.

图8 本文阵列与其他阵列的精度性能仿真结果对比

图9 本文阵列与其他阵列的分辨力性能对比

表1 空间谱所需计算点数对比

5 结语

提出一种利用组合阵列进行信号波达方向估计的算法.传统的DBF算法和MUSIC类超分辨测向算法通常要求阵列中的阵元间距≤半波长.在采用大口径阵列以提高算法性能的时候，就需要大量的阵元，导致系统复杂度大大提高.如果仍然采用大口径阵列，减少阵元数目，则会导致难以预测的阵列模糊问题.本文提出算法能够回避较少阵元的阵列产生的模糊问题，同时利用大的阵列口径提高算法的测向精度和分辨力性能，并且在一定程度上降低了计算复杂度和系统的硬件复杂度.

［1］SCHMIDT R.Multiple emitter location and signal parameter estimation［J］. Antennas and Propagation， IEEE Transactions on，1986，34(3):276-280.

［2］ ROY R，PAULRAJ A，KAILATH T.ESPRIT-A subspace rotation approach to estimation of parameters of cisoids in noise［J］.Acoustics，Speech and Signal Processing，IEEE Transactions on，1986，34(5):1340-1342.

［3］BOHME J.Estimation of source parameters by maximum likelihood and nonlinearregression［C］//Acoustics，Speech， and SignalProcessing， IEEE International Conference on ICASSP’84.［S.l.］:IEEE，1984:271-274.

［4］BRESLER Y.Maximum likelihood estimation of a linearly structured covariance with application to antenna array processing［C］//Spectrum Estimation and Modeling，1988，Fourth Annual ASSP Workshop on.Minneapolis:IEEE，1988:172-175.

［5］YAN Fenggang，JING Ming，QIAO Xiaolin.Low-complexity DOA estimation based on compressed MUSIC and its performance analysis［J］. SignalProcessing， IEEE Transactions on，2013，61(8):1915-1930.

［6］闫金山，彭秀艳，王咸鹏.基于酉变换的虚拟阵列DOA估计算法［J］.哈尔滨工业大学学报，2012，44(4):136-140.

［7］GAO Feifei，GERSHMAN A B.A generalized ESPRIT approach to direction-of-arrival estimation［J］.Signal Processing Letters，IEEE，2005，12(3):254-257.

［8］梁国龙，张柯，安少军，等.声矢量阵快速子空间方位估计算法［J］.哈尔滨工业大学学报，2014，46(7):76-80.

［9］ RAO B D，HARI K.Performance analysis of root-MUSIC［J］.Acoustics，Speech and Signal Processing，IEEE Transactions on，1989，37(12):1939-1949.

［10］KAVEH M，BARABELL A.The statistical performance of the MUSIC and the minimum-norm algorithms in resolving plane waves in noise［J］.Acoustics，Speech and Signal Processing，IEEE Transactions on，1986，34(2):331-341.

［11］ZHOU Changguo，HABER F，JAGGARD D L.A resolution measure for the MUSIC algorithm and its application to plane wave arrivals contaminated by coherent interference［J］.Signal Processing，IEEE Transactions on，1991，39(2):454-463.

［12］TAN K C，GOH Z.A detailed derivation of arrays free of higher rank ambiguities［J］.Signal Processing，IEEE Transactions on，1996，44(2):351-359.

［13］ MANIKASA， PROUKAKISC. Modelingand estimation of ambiguities in linear arrays［J］.Signal Processing，IEEE Transactions on，1998，46(8):2166-2179.

［14］HAUPT R L.Thinned arrays using genetic algorithms［J］.Antennas and Propagation，IEEE Transactions on，1994，42(7):993-999.

［15］贾维敏，林志强，赵鹏，等.一种多约束稀布线阵的天线综合方法［J］.电子学报，2013，41(5):926-930.

［16］陈客松，何子述.平面稀布天线阵列的优化算法［J］.电波科学学报，2009，24(2):193-205.

［17］唐斌，陈客松，杨晓波.圆形口径平面天线阵列的多约束稀布优化方法［J］.电波科学学报，2013，28(1):21-27.

［18］王维博.粒子群优化算法研究及其应用［D］.成都:西南交通大学，2012.

［19］HE Ziyuan，ZHAO Zhiqin，YANG Kai，et al.Solving ambiguity for sparse array via particle swarm optimization ［C］//International Conference on Computational Problem-Solving 2011.Chengdu:IEEE，2011:316-319.

［20］HE Ziyuan，ZHAO Zhiqin，NIE Zaiping，et al.Method of solving ambiguity for sparse array via power estimation based on MUSIC algorithm［J］.Signal Processing，2012，92(2):542-546.

［21］HE Ziyuan，ZHAO Zhiqin，NIE Zzaiping，et al.Resolving manifold ambiguities for sparse array using panar sbstrates［J］.Antennas and Propagation，IEEE Transaction，2012，60(5):2558-2562.

［22］AGRAWAL M，TAN K C.Higher rank ambiguity for star arrays［J］.Signal Processing，Elsevier，2004，84(12):2265-2269.

［23］冷文，王安国.均匀圆阵来波方向估计的解模糊算法［J］.天津大学学报:自然科学与工程技术版，2011，44(2):152-156.

［24］FRIENDLANDER B，WEISS A J.The resolution threshold of a direction-nding algorithm for diversely polarized arrays［J］.Signal Processing，IEEE Transactions on，1994，42(7):1719-1727.