双循环圆液力缓速器叶形设计方法

闫清东，穆洪斌，魏 巍，刘树成

(1.北京理工大学机械与车辆学院，100081北京;2.车辆传动国家重点实验室(北京理工大学)，100081北京)

液力缓速器作为机械主制动器的有效辅助制动装置，能使重型车辆在高速行驶或下长坡工况下，有效降低或保持行驶速度，维持车辆制动效能［1-3］.液力缓速器按循环圆数目主要可分为单循环圆式与双循环圆式(又称单腔式与双腔式).单循环圆液力缓速器多采用具有一定倾角的等厚直叶片，其叶栅结构较为简单，通过设置合适的叶片倾角以获取较高的制动力矩系数.双循环圆液力缓速器具有制动功率大，径向尺寸小等优点，在大功率轮式车辆上有广泛应用［4-5］，图 1即为某车用双循环圆液力缓速器结构图.双循环圆液力缓速器叶片多采用弯叶片结构，叶片整体呈轴向弯曲状，工作面与垂直轴面约成90°，避免了叶片间的相互遮盖，铸造拔模工艺得到一定简化，且利于动轮压力平衡孔的加工.液力缓速器叶栅系统叶形结构是决定缓速器制动功率密度的关键因素之一［6］，叶形设计传统方法为根据已有经验，对典型叶形参数采用手动方式建立设计模型，进行特性计算，反复建模工作冗繁.北京理工大学［7-8］针对等厚直叶片，采用离散点几何映射法，简化了直叶片叶形设计流程，方便了进一步的特性研究.

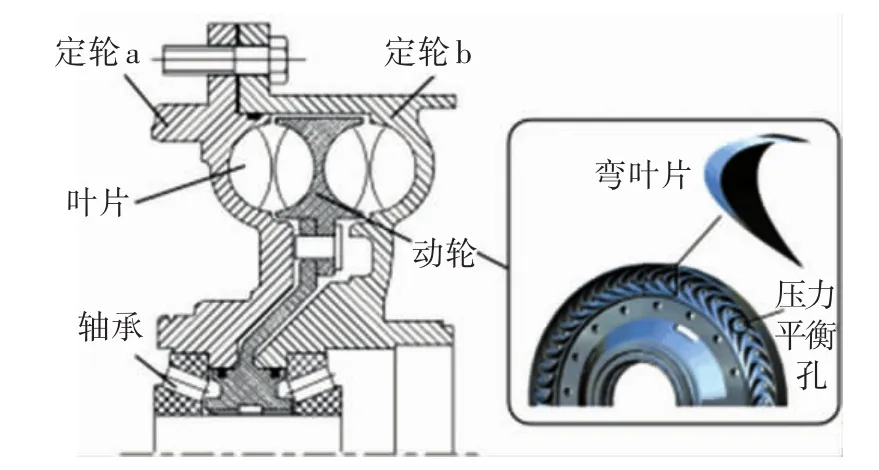
图1 双循环圆液力缓速器结构简图

鉴于双循环圆液力缓速器叶形结构复杂，为提高其制动性能，本文基于空间解析几何理论，提出相切圆弧叶形设计法，建立不同叶形参数的缓速器内流道模型.针对某型双循环圆液力缓速器样机，对叶形设计参数进行试验设计(DOE)，开展计算流体学(CFD)数值计算，并与样机制动性能进行对比研究.

1 相切圆弧叶形设计法

弯叶片结构简图如图2所示，鉴于弯叶片叶形结构特点，提出相切圆弧叶形设计法，其基本思想是:将叶片吸力面与压力面轴面(x-y面)投影曲线分别设定为由3段圆弧(内弧、中弧、外弧)相切构成［9-10］，通过空间解析几何法，建立流道曲线的数学模型，并通过Matlab程序，直接计算出不同叶形参数的缓速器周期流道模型点阵.

图2 叶片结构简图

液力缓速器动轮循环圆中径处分布有压力平衡孔，叶片的布置不应与平衡孔干涉，将叶片布置于两孔中间，即两中弧分别与以平衡孔为圆心，rk为半径的两圆相切，如图2(a)所示;叶片顶端径向投影为半径为ry的圆弧，其圆心在以循环圆中径R0为半径构成的轴向圆柱面上，如图2(b)所示.图3为叶片工作面包角图，其中为叶片压力面在x-y面投影的外轮廓设计曲线，即压力面与循环圆内壁相交曲线在x-y面的投影.

图3 叶片包角图

设计初始阶段确定压力面与循环圆内壁各段相交的点阵{Cn}.

式中:{Cn}(n=1，2，3)依次代表内弧、中弧、外弧的离散点.

压力面中弧圆心O1位于循环圆中径R0上，θa为中弧包角大小，可由此确定叶片压力面的弯曲程度.循环圆中径与中弧交点为点A，AO1与A1O1、A3O1的夹角为θa1、θa2，则有θa=θa1+θa2.通过计算A1、A2、A3、A4各点坐标，点阵{Cn}可表示为

对离散坐标点进行空间拟合，建立不同参数弯叶片压力面与循环圆内壁相交的空间轮廓曲线.叶片吸力面轮廓曲线受到压力面几何约束，其参数可由工作面几何参数表示:

由于较大的叶片厚度会导致油液在循环圆内流动过程中产生较大的收缩与扩散损失，因此循环圆入、出口叶片厚度应尽量小，因此设定与为较小常数 Δl.另外，吸力面半径rb1、rb3亦可由参数θa1、θa2、ra1、ra2、ra3与 Δδ推导出，计算流程图如图4.

由此，即可对于叶片吸力面的空间轮廓曲线进行求解.图5为单周期流道周期面与叶片工作面几何关系示意图，周期面a、b点阵可通过叶片压力面坐标旋转获得.D(xD，yD，zD)为压力面外轮廓空间曲线上任意一点，记为

{D}={(xDi，yDi，zDi)，i=1，2，…，m}，

其中

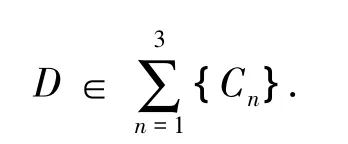
图 4 rb1与rb3计算流程图

图5 周期面分布图

以Oz(0，0，zD)为圆心，OzD为半径的与周期面a、b分别交于点P(xP，yP，zP)、Q(xQ，yQ，zQ)，其中 ∠POD=α1，∠QOD=α2.液力缓速器叶片在循环圆周向上均匀分布，通过求解相邻叶片间的间隔角即可得到单周期流道所占整个循环圆的角度α，α=α1+α2=360°/Z，其中Z为叶片数目.

在△OPD中，由余弦定理可得

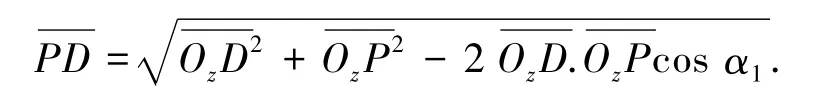
D、P两点位于同一个圆柱面，且zP=zD，由空间两点距离公式可得

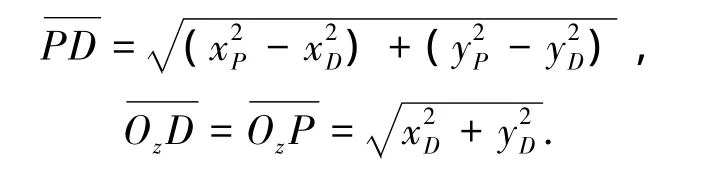
联立求解，可解出周期面a上离散后任意一点坐标P(xP，yP，zP)，同理可解出周期面b上离散点坐标Q(xQ，yQ，zQ)，记为

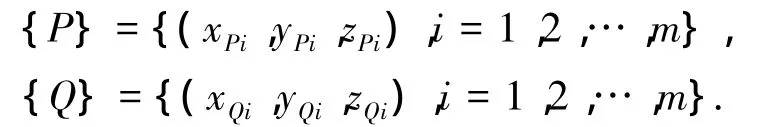
综上，提取出弯叶片叶形设计参数为

利用以上设计变量即可建立不同叶形参数的弯叶片液力缓速器周期流道模型.图6为只改变θa1与θa2，而其余参数保持不变的动轮流道设计结果.

图6 动轮流道设计结果

2 实例设计

针对某双循环圆液力缓速器样机模型，采用“相切圆弧叶形设计法”对其叶形参数开展DOE设计研究，各参数设计区间取为

基于商业软件Isight5.7搭建集成仿真平台，编辑脚本文件，以实现流道建模，网格划分，流场计算以及后处理等过程的自动连续进行.采用优化拉丁方设计方法在参数区间内生成435组均布的设计点［11-12］.基于相切圆弧叶形设计法获得单周期流道模型，利用ICEM CFD14.0软件对其进行非结构网格划分，设置全局网格尺寸为2 mm，并对叶片表面、周期面与交互面网格进行局部加密，获得单周期网格模型，如图7所示.其中，网格整体质量高于0.35，网格总数约为400 000.

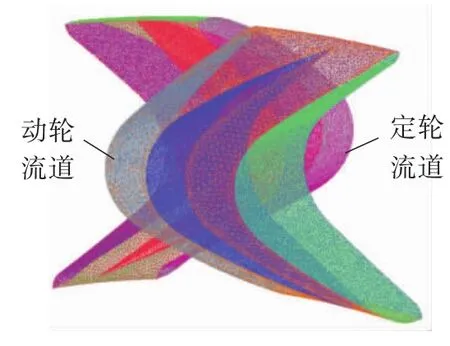
图7 单周期网格模型

利用ANSYS CFX 14.0流体动力学仿真软件对网格模型进行数值计算.在CFD求解中，湍流模型采用结合了自动壁面函数的切应力输运SST模型，采用级联法确定动轮与定轮的数据交互性边界条件，使用全隐式多网格耦合算法对计算模型进行黏性流动计算［13-15］，此计算方法亦被用于双循环圆液力缓速器样机数值求解中.仿真采用的计算机配置如表1所示.

表1 计算机配置

435次计算总用时约为143 h，将设计点计算结果进行降序排列，可得到与制动力矩呈单调关系的设计点序列.图8即为动轮转速1 000 r/min时，重排后的DOE设计结果与样机制动力矩对比图.

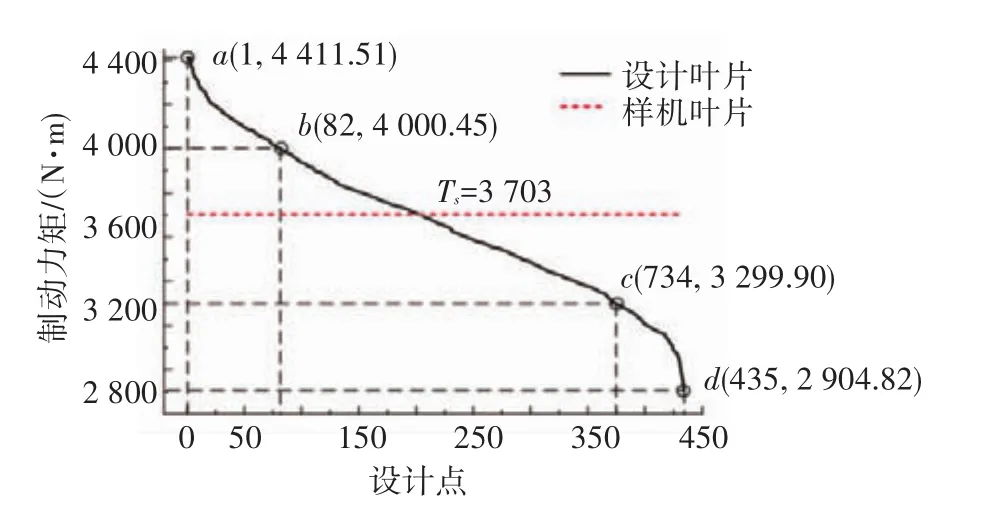
图8 设计叶片与样机叶片制动力矩对比

设计叶片制动力矩变化区间为［2 904.8，4 411.5］，而 样 机 叶 片 制 动 力 矩 为3 703 N·m.在循环圆尺寸与叶片数目一致的情况下，DOE设计叶片较样机叶片的制动力矩变化率为-21.6%～19.1%.由此可见，基于相切圆弧叶形设计法的设计叶片制动力矩包含样机叶片，且具有较大的变化范围，以满足不同制动功率车辆的使用需求.

如图8所示，在DOE设计计算结果中，按制动力矩大小均匀选取4个设计点a、b、c、d，叶形参数如表2所示，其制动力矩大小关系为:Ta＞Tb＞Ts＞Tc＞Td.

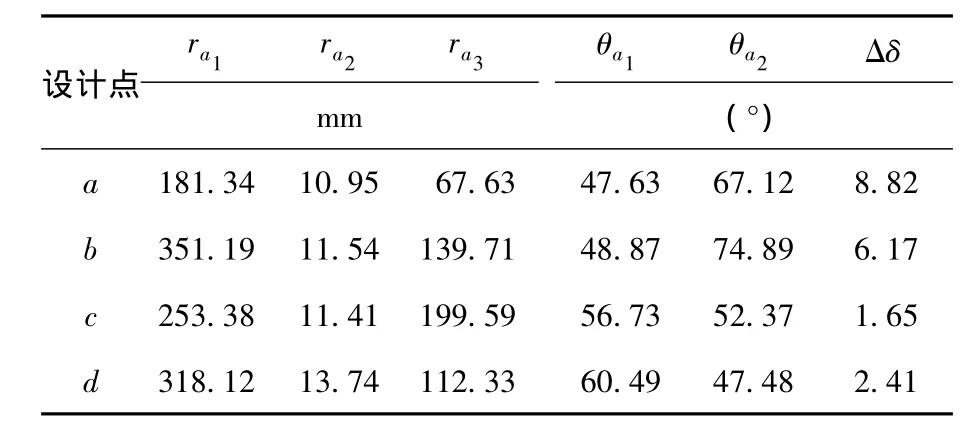
表2 叶形设计参数

为研究各叶形设计参数对制动力矩的影响，有必要对其进行敏感性分析.经过DOE设计计算后，可获得叶形参数对制动力矩影响的Pareto图和主效应图，如图9所示.Pareto图表征了自变量对因变量的影响程度，主要有线性相关程度、平方相关程度、自变量交互影响程度;主效应图则表示了因变量随自变量的变化关系.由图9(a)可知，参数 Δδ、θa2、ra2对制动力矩T的影响较大，其中ra2、θa2与T呈现明显的二次相关性，这可由图9(b)主效应图看出，ra2、θa2与T的关系均近似为开口向下的抛物线;而Δδ与T的线性关系较为明显，T随Δδ的上升单调递增.对比表2中设计点叶形参数可见，设计点a的参数Δδ取值最大，且θa2与ra2均近似取到主效应曲线力矩峰值处，因此制动性能最优，而对于设计点d，其Δδ取值较低，而θa2与ra2取值均处于各自设计区间边缘，综合起来制动性能最差.

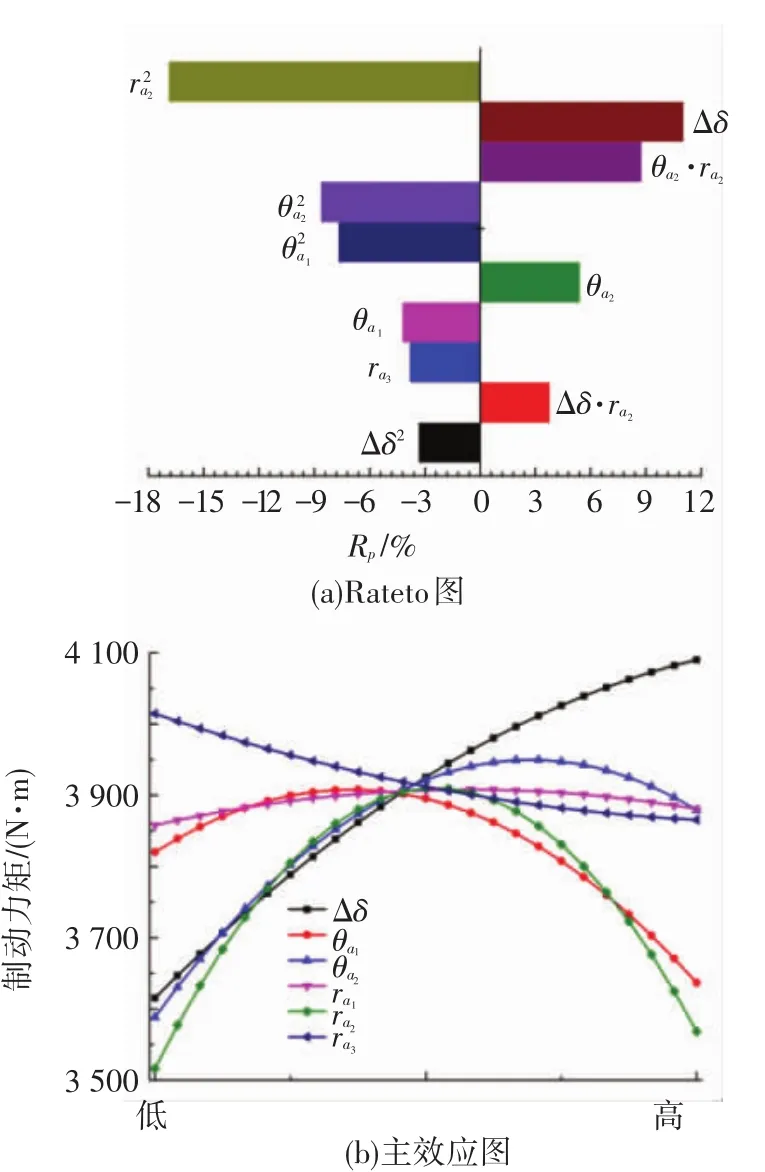
图9 敏感性分析图

图10为不同转速下DOE设计叶片与样机制动性能计算结果，并与原样机试验数据进行对比.其中试验结果来源于某重型车辆厂对液力缓速器样机的制动性能台架试验.

可见，不同转速下样机仿真结果与试验数据吻合较好，平均相对误差仅为4.8%，制动力矩系数数值亦较为接近.由于仿真过程未考虑缓速器工作腔进出口以及叶片铸造圆角对流场产生的影响，因此计算误差在可接受范围，证明了此数值计算方法具有良好的可靠性，应用相同计算方法的DOE设计计算结果亦应具有一定精度.

由图10(a)中制动力矩曲线分布可知，转速范围内设计叶片a的整体制动性能最佳，设计叶片d的制动性能最差，而样机叶片制动力矩介于设计叶片b、c之间，其中设计叶片a的制动力矩较样机仿真结果平均上升了20.55%.制动功率密度大小主要由制动力矩系数体现，力矩系数则主要取决于叶形结构、叶片数目等参数，而与动轮转速、循环圆直径无关.由图10(b)可见，相同叶形不同动轮转速下，制动力矩系数近似恒定.通过对比各设计点平均力矩系数亦可获得与图10(a)相似的分析结果，由此可见，在不改变缓速器循环圆结构尺寸与叶片数目的前提下，通过设定合适的叶形参数，缓速器的制动功率密度可得到显著提高.

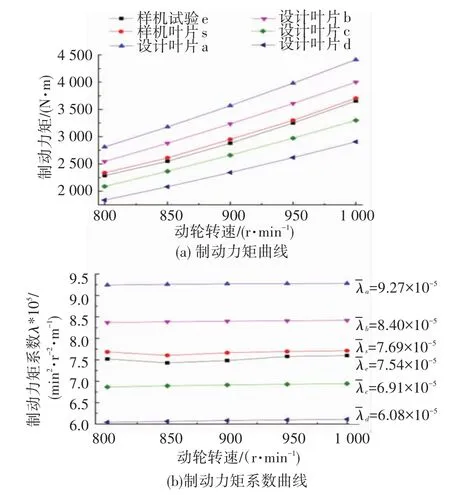
图10 制动性能对比图

3 结论

1)基于相切圆弧叶形设计法，提出弯叶片叶形设计方法，实现了双循环圆液力缓速器内流道模型的快速生成.

2)制动性能对比结果表明，样机叶片计算结果较试验数据的平均误差＜5%，证明了数值计算方法具有良好的可靠性，DOE设计计算结果亦应具有一定精度.

3)结合优化拉丁方设计方法对叶形参数开展设计，结果表明，设计叶片制动力矩可满足缓速器样机的使用需求，且在叶形参数设计区间内，其制动力矩较样机可产生-21.6%～19.1%的变化范围.

4)通过设定合适的叶形参数，利用相切圆弧叶形设计法可有效提高缓速器制动功率密度，此方法适用于双循环圆液力缓速器弯叶片叶形设计研究.

［1］魏巍，李慧渊，邹波，等.液力缓速器制动性能及其两相流分析方法研究［J］.北京理工大学学报，2010(11)，1281-1284.

［2］李雪松，刘春宝，程秀生，等.基于流场特性的液力缓速器叶栅角度优化设计［J］.农业机械学报，2014.45(6):20-24.

［3］闫清东，邹波，魏巍，等.液力减速器充液过程瞬态特性三维数值模拟［J］.农业机械学报，2012.43(1)，12-17.

［4］Allison Transmission Inc.MD/HD/B series on-highway transmissions operator’s manual［R］.Indiana:Allison Transmission Inc，2005.

［5］Allison Transmission Inc.3000/4000 operator’s manual［R］.Indiana:Allison Transmission Inc，2010.

［6］严军，何仁.液力缓速器叶片变角度的缓速性能分析［J］.农业机械学报，2009，40(4):206-209.

［7］邹波，陈日军，唐正华，等.液力减速器内流道数值建模方法研究［J］.机床与液压，2011，39(9):100-104.

［8］闫清东，邹波，魏巍.液力减速器叶片前倾角度三维集成优化［J］.吉林大学学报:工学版，2012，42(5):1135-1139.

［9］王企鲲.具有组合式叶片的导流型垂直轴风力机气动性能的数值研究［J］.机械工程学报，2011，47(12):126-132.

［10］王企鲲.导流型垂直轴风力机内部流场数值模拟中若干问题的探讨［J］.机械工程学报，2011，47(4):147-154.

［11］JIN R C，CHEN W，SUDJLANTON A.An efficient algorithm for constructing optimal design of computer experiments［J］.Journal of Statistical Planning and Inference，2005(1):268-287.

［12］ALEJANDRO S H.Breaking barriers to design dimensions in nearly orthogonal latin hypercubes［D］.Monterey:Naval Postgraduate School，2008.

［13］KIM B S，HA S B，LIM W S，et al.Performance estimation model of a torque converter part I:Correlation between the internal flow field and energy loss coefficient［J］.International Journal of Automotive Technology，2008，9(2):141-148.

［14］GRIGORIADIS D G E，BARTZIS J G.Efficient treatmentof complex geometries for large eddy simulations of turbulent flows［J］.Computers＆ Fluids，2004，33(2):201-222.

［15］de la FUENTE P，STOFF H，VOLGMANN W，et al.Numerical analysis into the effects of the unsteady flow in an automotive hydrodynamic torque converter［C］//Proceedings of the World Congress on Engineering.London:Newswood Ltd，2011:2405-2410.