光纤熔融拉锥中拉力控制方法与电磁力仿真
张 伟,荣伟彬,王乐锋,路 遥,孙立宁
(机器人技术与系统国家重点实验室(哈尔滨工业大学),150080哈尔滨)
保偏光纤耦合器是应用保偏光纤制作的光耦合器,是实现线偏振光耦合、分光以及复用的关键器件,广泛应用于光纤传感和相干通信中[1-2].熔融拉锥[3-4]是将光纤两端固定并使其具有一定的张力,加热光纤,使其受热部分处于熔融状态,同时在两端拉伸光纤,使受热部分即光纤熔锥区形成锥型或者哑铃型,此方法是保偏光纤耦合器制造中最重要的方法.与磨抛法和腐蚀法相比,熔融拉锥具有热稳定性好、器件附加损耗小的特点.熔融拉伸过程由拉伸速度、熔融温度和拉力3个工艺参数共同控制,其中光纤两端的拉力直接影响保偏光纤耦合器的性能.目前,光纤拉锥系统通常是由拉锥运动部分、加热部分和光纤装夹部分等组成.拉锥运动部分采用精密步进电机(直流电机)运动平台,由计算机实现对拉伸速度的控制.拉伸力由运动平台的运动产生,当运动平台的速度不同时,其产生的拉伸力也不同.光纤的主要成分是石英玻璃,是一种热黏弹性材料,黏弹性变形和加热温度有关,因而当运动平台的运动速度不变时,光纤的加热温度不同,其黏弹性变形不同,由运动平台产生的拉力也不同,因此很难对拉伸力进行实时控制[5-8].PAL等[9]在熔融拉锥运动平台上安装弹簧,解决了光纤在拉伸过程中光纤的两端拉力突然变化的问题;但是当弹簧的伸长不相同时,光纤受到的拉力也不同,不容易实现拉伸过程中的拉力控制.吕迅等[10]在拉锥机构内侧安装高敏感度的张力传感器,通过调节拉锥电机的速度控制张力的大小,因而张力在一定范围内波动.
针对保偏光纤耦合器制作过程拉力控制问题,本文提出了一种计算机在线拉力控制方法,通过检测光纤支架的旋转角度、控制线圈中的电流,进而实现拉力的控制.介绍拉力控制系统的组成及其工作原理,对运动中的永磁铁和线圈之间的电磁力进行三维有限元仿真,通过仿真结果建立线圈电流、支架旋转角度与电磁力的数学关系,并且验证了该方法的可行性.
1 拉力控制系统组成及工作原理
保偏光纤熔融拉锥拉力控制系统原理如图1所示,主要由拉伸机构、电磁线圈、圆光栅、DA输出卡、运动控制卡和计算机等组成.拉伸机构有鼓轮连接片、联动鼓轮、光纤支架以及底座等构成如图2所示.

图1 保偏光纤熔融拉锥拉力控制系统原理

图2 保偏光纤熔融拉伸机构结构
控制系统工作原理如下:计算机经DA输出卡控制输出电压,控制线圈中电流的大小,电流经通电线圈产生磁场,并与光纤支架上的永磁铁作用产生相互吸引的电磁力,由此光纤支架产生拉力.同时,由于两个鼓轮之间有两片连接片连接,因而两鼓轮在垂直面内的旋转运动过程中是联动的.圆光栅的玻璃盘和鼓轮连接在一起,圆光栅可以检测出鼓轮旋转角度的变化,进而得到当前光纤支架的旋转角度,由此根据光纤支架的长度计算得到光纤的拉伸长度.采用云杉素将光纤固定在光纤支架上,光纤在加热源和光纤支架拉力的作用下,完成熔融拉锥运动.
拉伸机构采用超薄弹片连接,薄片的弯曲弹力相对于拉伸力可以忽略,两侧光纤支架产生的拉力相等,并且两侧光纤支架旋转的角度相同.当光纤支架旋转角度在0°~5°时,能够满足光纤熔融拉锥的要求.单个光纤支架的受力分析如图3所示,光纤支架的力矩平衡关系为
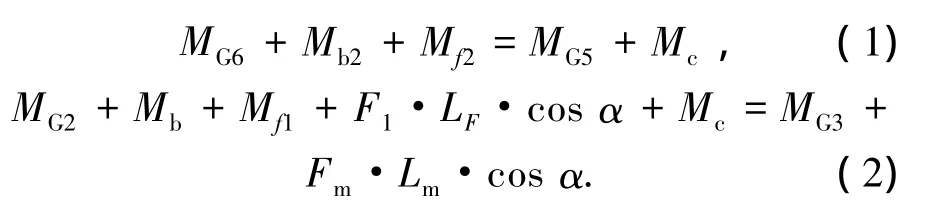
式中:Mb2(Mb1)为左(右)支架上的连接片与其紧固螺栓产生的力矩;Mf2(Mf1)为左(右)支架旋转过程摩擦力产生的力矩;MG6(MG2)为左(右)支架下端配重产生的力矩;MG5为左支架产生的力矩;α为支架中心线与垂直方向的夹角;MG3为右支架、永磁铁及固定架产生的力矩;F1为右支架产生的拉力;LF为当α=0°时,F1到支架旋转中心O1的距离;Lm为当α=0°时,电磁力Fm到支架旋转中心O1的距离;Mc为连接片产生的力矩.
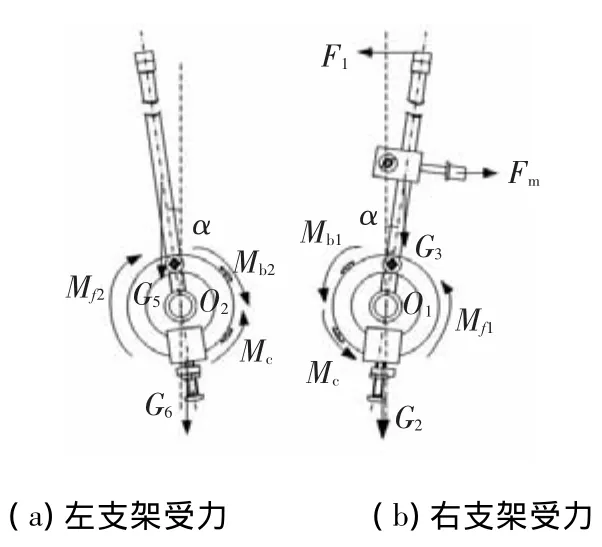
图3 单个光纤支架受力图
由式(1)可知,调节左支架下端配重的位置,改变力矩MG6的大小,使Mc=0.由式(2)可知,当F1=0,Fm=0,调节右支架下端配重的位置,改变力矩的MG2大小,使其满足
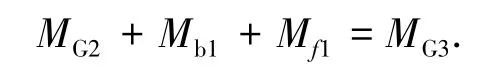
光纤支架整体的受力如图4,满足力矩平衡
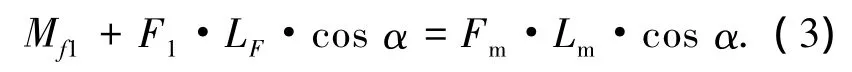
光纤支架的支撑轴承采用精密深沟球轴承支撑,精密深沟球轴承的摩擦系数约为0.001 0~0.001 5,在光纤支架旋转中摩擦力很小,相对拉力可以忽略,将式(3)简化为
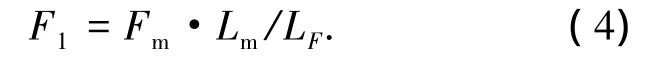
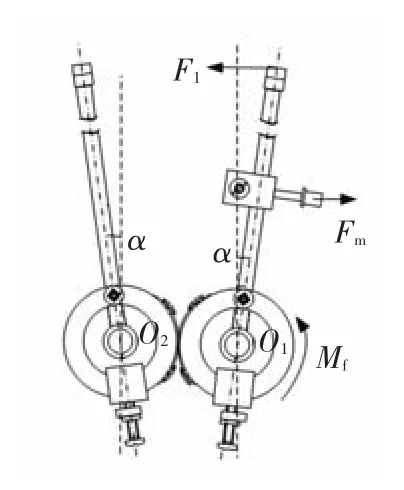
图4 光纤支架整体受力示意
在拉伸过程中,永磁铁的运动轨迹是空间弧线,永磁铁和线圈之间的距离变化,当线圈中的电流恒定时,线圈和永磁铁的电磁力变化,因此光纤支架产生的拉力发生改变.
2 电磁力的分析与仿真
2.1 理论分析
圆柱型永磁铁是最常用的永磁铁之一,广泛地应用在编码器、制动器、马达等器件中.对于一个高度为Z0,半径为a的圆柱型永磁铁,磁化方向是沿着Z向磁化,外部磁场分布在(r,θ,z)的磁感应分布B为[11-12]

式中:K(k)和E(k)分别是第一类和第二类完全椭圆积分,且

在电磁场中,常用计算电磁力的方法有3种:洛伦兹力(Lorenz Force)法、麦克斯韦应力张量(Maxwell Stress Tensor)法和虚位移(Virtual Work)方法[13].其中,洛伦兹力方法适合于计算载流体在磁场中的受力.永磁铁受到的电磁力Fm与通电线圈受到的电磁力Fc为一对作用力与反作用力,根据牛顿第三定律和洛伦兹力定律,永磁铁受到的电磁力为

式中:f为线圈单位体积受到的电磁力,J为线圈的电流密度,B为线圈受到的磁感应强度.
2.2 有限元分析
在支架的运动过程中,圆柱型永磁铁进入线圈的通孔中,采用二维仿真计算无法准确计算出电磁力.为了计算的准确性,本文建立三维的仿真模型,以光纤支架的旋转中心为原点建立OXYZ三维坐标系,如图5所示.线圈支架的材料为尼龙,是绝缘材料,在仿真中可将线圈简化.钕铁硼有极高的磁能积和矫顽力,同时具有高能量密度的优点,因此选取钕铁硼作为永磁铁[14].永磁铁的外形尺寸为Φ6 mm×10 mm,由高斯计GV-300测得表磁为389 mT.线圈高度为40 mm,内径为20 mm,外径为30 mm,匝数为1 756匝.在光纤支架运动过程中,永磁铁与YOZ面的夹角随着运动角度变化.永磁铁在XOY平面运动示意图如图6所示:假设永磁铁中心B点的坐标为(px,py),则光纤支架旋转θ后,永磁铁的中心轴与水平面夹角为θ,B点的坐标为

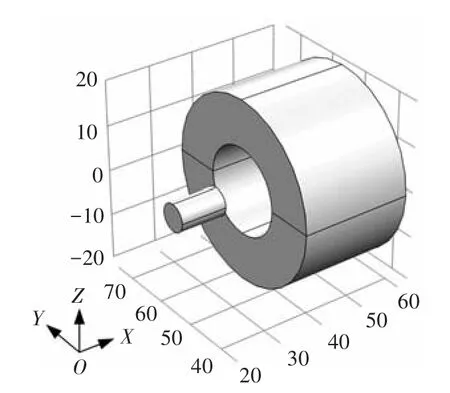
图5 电磁力仿真模型

图6 永磁铁运动示意
建立立方体空气场来模拟空间的磁场分布情况,取立方体的边长130 mm,边界采用磁绝缘边界条件,即磁矢位n×A=0,选择初始值磁矢能为0 Wb/m[15-16].网格划分采用自由四面体划分,为了提高计算的精度和速度,对线圈和永磁铁采用细化的网格划分,对立方体空气场采用标准的网格划分.划分后的有限元网格数为44 743,划分后的网格如图7所示.

图7 网格划分
线圈中通入0.15 A电流时,在X=35 mm通电线圈的磁场分布如图8,图9是AB上磁感应强度的分布图,其中AB穿过线圈的中心轴.

图8 X=35 mm的磁感应分布

图9 AB上磁感应强度分布
由图8和9可知,通电线圈上方的磁感应强度与到线圈中心轴的距离有关,当距离小于线圈的内径(20 mm)时,随着距离的减小,磁感应强度逐渐减少,在线圈中心轴上的磁感应强度最小为5.147 mT,与通过解析式[17]得到的 5.196 mT 基本相同.AB上的磁感应强度最大值与最小值相差0.3 mT,磁感应强度的变化率较小.当距离为线圈的内径时,磁感应强度最大,随着距离的增大,磁感应强度急剧减小.图10为Z=0时的磁感应强度分布图,图11为CD线上的磁感应强度分布图,其中C、D为线圈中心轴的两点,其两点关于线圈垂直轴对称,可以看出,通电线圈磁感应强度分布关于线圈垂直轴对称,沿着线圈中心轴上磁感应分布是先减少后增大,在线圈中心达到最大值,在线圈的右轮廓附近,磁感应强度的变化接近线性变化.

图10 Z=0的磁感应分布

图11 CD上磁感应强度分布
2.3 结果与讨论
线圈周围的磁感应强度与其通入的电流有关,因而永磁铁上的电磁力与电流有关,图12为旋转角度θ=0°时,电磁力与线圈中电流的关系图,通过最小二乘拟合得到线圈中的电流与电磁力是线性关系,关系表达式如下:

式中:Fm为永磁铁产生的电磁力(N),Ⅰ为线圈中的电流(A).
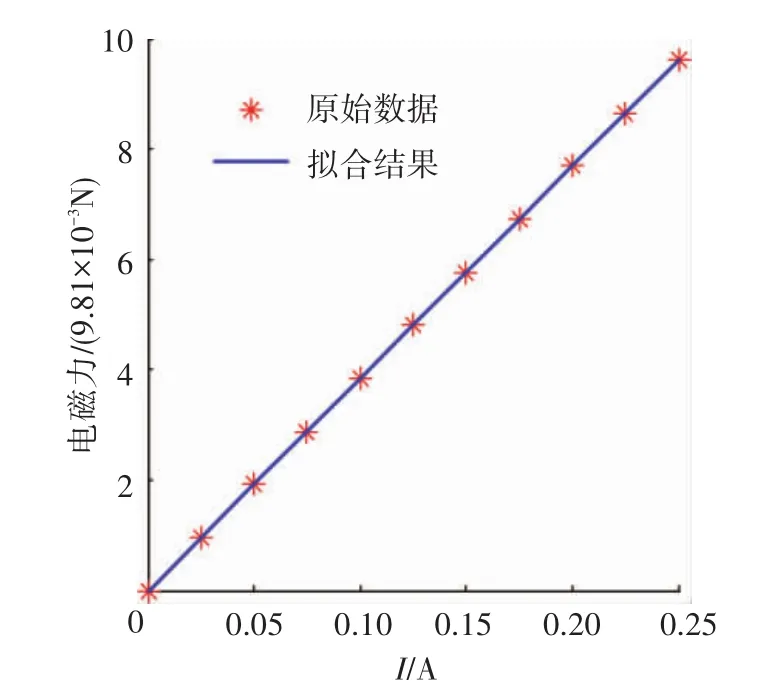
图12 θ=0°时,电磁力与电流的关系
当支架旋转角度θ发生变化时,永磁铁的位置发生变化,线圈周围的磁场会发生变化,永磁铁产生的电磁力也发生变化.图13为线圈中的电流恒定时,支架的旋转角度与电磁力的变化关系图.当电流恒定时,旋转角度θ与电磁力Fm呈线性关系,但当电流变化时,电磁力Fm和旋转角度θ的线性关系也发生变化.定义电磁力变化率KFθ为当线圈中的电流恒定时,电磁力变化与旋转角度变化的比值,即
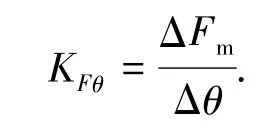
式中:ΔFm为永磁铁上电磁力的变化(N),Δθ为支架旋转角度θ的变化(°).

图13 支架旋转角度与电磁力的关系
图14为电磁力变化率和线圈中电流的关系图,可以看出电磁力变化率与线圈中的电流呈线性变化,通过最小二乘拟合得

当支架旋转角度不同时,线圈电流与电磁力的线性关系不同.定义电磁力标定值KFⅠ为光纤支架旋转角度不变时,电磁力变化与电流变化的比值,即

式中:ΔFg为永磁铁上电磁力的变化(N);ΔⅠ为线圈中电流的变化(A).
图15为电磁力标定值和旋转角度的关系图,由图可知,电磁力标定值与支架的旋转角度呈线性变化,关系表达式为

由式(5)~(7)得到Fm、Ⅰ、θ的关系式为
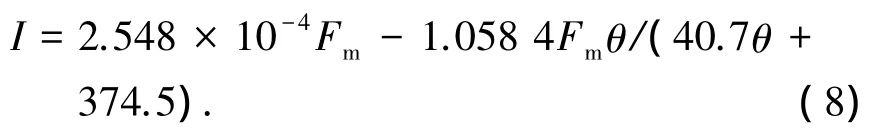
由式(4)和式(8)可得到F1、Ⅰ和θ的关系式为


图14 电流与电磁力变化率的关系

图15 支架旋转角度与电磁力标定值的关系
当拉力F1为定值时,由式(9)可以得Ⅰ和θ的关系,如图16所示,当拉力保持恒定时,输入的电流随着光纤支架旋转角度的增大而减少.当光纤支架旋转角度改变时,通过改变线圈的电流,改变电磁力,实现拉力的控制,图17中为通过控制线圈中的电流得到拉力和光纤支架旋转角度的关系图,由图中看出拉力基本保持恒定,控制误差为1.03%.因此当光纤支架的旋转角度改变时,改变线圈中的电流,改变电磁力,实现光纤支架拉力的控制.
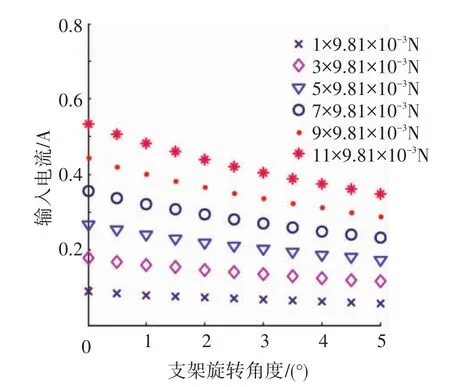
图16 拉力恒定时电流和光纤支架旋转角度关系

图17 控制电流后光纤支架旋转角度与拉力的关系
3 结论
1)本文提出了一种实时拉力控制方法,保偏光纤熔融拉锥拉力控制系统由计算机、拉伸机构、圆光栅和控制电路等组成,通过检测光纤支架的旋转角度,控制线圈中的电流,实现对拉力的实时控制.
2)对拉伸机构进行受力分析,确定了拉力和电磁力之间的关系.建立了拉伸机构的三维空间模型,确定了永磁铁空间运动轨迹.
3)对永磁铁和线圈之间的电磁力进行三维有限元仿真,通过计算得到了线圈中的电流、支架旋转角度与拉力的关系,并且通过仿真验证了该方法的控制误差为1.03%.该方法对保偏光纤耦合器的制造具有重要的指导意义.
[1]DAVÉ D P,AKKIN T,MILNER T E.Polarization-maintaining fiber-based optical low-coherence reflectometer for characterization and ranging of birefringence[J].Optics letters,2003,28(19):1775-1777.
[2]孟克,鲁标,李艳昌,等.水声信号的光纤DSPI检测[J].哈尔滨工业大学学报,2004,36(8):1118-1120.
[3]KAWASAKI B S,HILL K O,LAMONT R G.Biconicaltaper single-mode fiber coupler[J].Optics Letters,1981,6(7):327-328.
[4] LAMONT R G,JOHNSON D C,HILL K O.Power transferin fused biconical-tapersingle-mode fiber couplers:dependence on external refractive index[J].Applied optics,1985,24(3):327-332.
[5]HARUN S W,LIM K S,TIO C K,et al.Theoretical analysis and fabrication of tapered fiber[J].Opti-International Journal for Light and Electron Optics,2013,124(6):538-543.
[6] HSIEH C S,WU T L,CHENG W H.An optimum approach for fabrication of low loss fused fiber couplers[J].Materials Chemistry and Physics,2001,69(1):199-203.
[7]WANG Y,LIU H.The comparison of two methods to manufacture fused biconical tapered optical fiber coupler[C]//Photonics and Optoelectronics Meetings 2009.[S.l.]:International Society for Optics and Photonics,2009:751418-1—751418-9.
[8]帅希士.电加热式熔融拉锥机的运动控制研究[D].长沙:中南大学,2006.
[9]PAL B,CHAUDHURI P,SHENOY M.Fabrication and modeling of fused biconical tapered fiber couplers[J].Fiber and integrated optics,2003,22(2):97-117.
[10]吕迅,官洪运.熔融拉锥控制系统的改进[J].江南大学学报:自然科学版,2003,2(6):597-600.
[11]EBRAHIMI B,KHAMESEE M B,GOLNARAGHI M F.Design and modeling of a magnetic shock absorber based on eddy current damping effect[J].Journal of Sound and Vibration,2008,315(4):875-889.
[12]AGASHE J S,ARNOLD D P.A study of scaling and geometry effects on the forces between cuboidal and cylindrical magnets using analytical force solutions[J].Journal of Physics D:Applied Physics,2008,41(10):1-9.
[13]张存山.永磁无刷牵引电机电磁性能研究[D].北京:北京交通大学,2006.
[14]LEVENTIS N,GAO X.Nd-Fe-B permanent magnet electrodes:Theoreticalevaluation and experimental demonstration of the paramagnetic body forces[J].Journal of the American Chemical Society,2002,124(6):1079-1088.
[15]ALFERENOK A,WERNER M,GRAMSS M,et al.Numerical optimization of the magnet system for the lorentz force velocimetry of electrolytes[J].International Journal of Applied Electromagnetics and Mechanics,2012,38(2):79-92.
[16]ZIOLKOWSKI M,BRAUER H.Fast computation technique of forces acting on moving permanent magnet[J].IEEE Transactions on Magnetics,2010,46(8):2927-2930.
[17]PAWASHE C,FLOYD S,SITTI M.Modeling and experimental characterization of an untethered magnetic micro-robot[J].The International Journal of Robotics Research,2009,28(8):1077-1094.

