基于ANSYS轨道不平顺条件下轮轨系统频谱动力响应分析

魏云鹏，吴亚平，陈 鄂，段志东，王良璧

(1.兰州交通大学土木工程学院，兰州 730070;2.兰州交通大学机电工程学院，兰州 730070)

基于ANSYS轨道不平顺条件下轮轨系统频谱动力响应分析

魏云鹏1，吴亚平1，陈 鄂1，段志东1，王良璧2

(1.兰州交通大学土木工程学院，兰州 730070;2.兰州交通大学机电工程学院，兰州 730070)

为了分析轮轨系统在轨道不平顺功率谱激励下的动力响应，根据动力学原理并结合有限元理论，建立了轮轨接触的有限元模型，对轮轨系统进行静力分析和频谱分析，获得轮轨接触的基本特性和轮轨系统不同部位位移和加速度响应的谱值，计算结果表明，车体竖向位移最大谱值对应的频率为1.669Hz，而其最大加速度谱值所对应的频率为105.25Hz;车轴和车轮底面最大竖向位移和加速度谱值所对应的频率分别为66.27Hz和66.28Hz;同时结果显示，位移和加速度响应谱值随着列车运行速度的增加也是逐渐变大的。

轮轨接触;不平顺;功率谱;动力响应;有限元

随着我国高速铁路的快速发展，列车运行速度不断的提高，轨道的不平顺是引起列车振动和限制车速的主要因素之一，轨道的不平顺主要有4种，即高低不平顺、水平不平顺、轨距不平顺和方向不平顺［1］。近年来有许多学者研究了轨道不平顺对列车和铁路路基的影响。钱学军研究推导了轨道不平顺功率谱密度在空间和时间频率之间的转换，并设计了新的算法对轨道不平顺功率谱密度在时间频率上的模拟［2］;徐磊等人利用小波理论和Wigner-Ville分布对轨道不平顺信号识别进行了研究，其结果指出小波理论和Wigner-Ville分布能够有效地分析轨道的不平顺［3］;项盼等人研究了在轨道不平顺条件下不确定车轨耦合系统下的响应，并同其他的计算方法进行了对比［4］;冯青松等人建立了车辆-轨道-路基-地基的计算模型［5］，研究计算了在轨道不平顺条件下的地基振动情况;梁波等人将由轨道不平顺引起的车辆附加荷载以正弦函数的形式施加在路基的有限元模型上［6］，对路基的动力响应进行了探讨。还有一些学者对铁路重载技术和道岔进行了研究［7-8］。

以上的研究揭示了在轨道不平顺条件下车辆-轮轨-路基的动力特性，但在以上的研究中多数用Hertz理论来处理轮轨关系，将钢轨视为弹性的连续梁，用多刚体来模拟车辆，并且缺少三维的计算模型。本文借助于ANSYS有限元软件，建立了包含两组轮对的三维轮轨接触有限元模型，考虑了钢轨和车轮之间实际的接触情况，并且采用双线性随动强化的本构关系模拟轮轨的材料特性，最后引入轨道不平顺功率谱值，计算了轮轨系统的动力响应。

1 三维轮轨有限元模型

1.1 有限元模型

模型中车轮踏面为LM踏面，钢轨为CHN60型钢轨，1∶20的轨底坡。轮轨接触的有限元模型如图1所示。

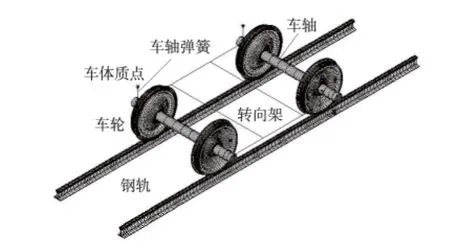
图1 有限元模型

轮轨接触的有限元模型包含将车体简化的集中质点、车轴弹簧、转向架、车轴、车轮和钢轨。在轮轨的接触区域用20节点的186单元进行离散，对实际转向架进行了简化并用189梁单元模拟，其他实体构件用8节点的185单元模拟，并且在轮轨接触区域将网格进行了细化，这样既可以确保计算精度，又可以减少单元数量。轮轨之间的接触用标准的接触对模拟，其目标单元为TARGE170单元，接触单元为 CONTA174单元;在建模的过程中使用了多点约束的建模方法。模型总共有112 852个单元，313 072个节点，钢轨总长度为6.75 m。

1.2 计算参数

车辆单个轴重为160 kN;单个车轴弹簧的竖向刚度为444 kN/m［9］，本文的模型中按照两个弹簧并联取值;车轴的弹性模量为207 GPa，泊松比为0.2，密度为7 800 kg/m3;转向架的材质为16Mn钢，其弹性模量为200 GPa，泊松比为 0.25［10］，密度为7 800 kg/m3;车轮和钢轨材料的本构关系根据文献［11］确定，其密度为7 800 kg/m3。

2 轨道不平顺谱

轨道不平顺是由许多波长和幅值大小不一的随机不平顺波组成的，以往的研究往往用几个确定的函数来描述轨道的不平顺，这将会引起较大的误差;而轨道不平顺功率谱率谱密度则可以较全面地反映轨道的不平顺状态，目前已成为工程中常用的表述轨道不平顺的方法。

功率谱密度的大小与铁路线路的等级和结构等众多因素有关，根据大量的实测数据已经拟合出几种谱值的表达式［12］，在国内外均有研究。已有的功率谱表达式主要是在空间域上的，但在实际的计算中往往是在时间域(或频率域)内进行的，在本文的计算中先将功率谱根据已有的研究从空间域转换为频率域［13］，再引入到有限元模型中进行计算。

式中，SV(Ω)为功率谱密度，Ω;k为安全系数，一般取0.25;AV为粗糙度常数，cm2·rad/m;ΩC为截断频率，rad/m。

空间波数Ω(rad/m)与频率f(Hz)和车速V(m/s)之间的关系如下

根据能量守恒原理，即

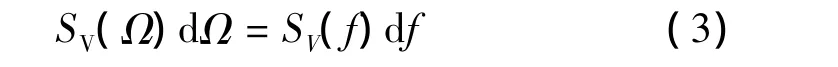
由式(1)、式(2)和式(3)得到用频率表达的功率谱密度表达式:

本文的计算中 k为 0.25，AV为0.033 9 cm2·rad/m，车速取 50、100 km/h 和 150 km/h，fC由下式确定

3 计算结果

在整个计算中先进行了系统的静力分析，获取了轮轨接触区域的基本特性，然后进行了模态分析，得到整个系统的振动频率和振型，再对系统进行谱分析，获得了轮轨系统不同位置处谱值。

3.1 静力计算结果

通过静力计算，获得轮轨接触区域的形状，轮轨接触区域的形状如图2所示。结果显示轮轨接触应力为647 MPa，接触斑的面积为256.3 mm2，并且从图中可以看出轮轨接触斑的形状并非为椭圆形。

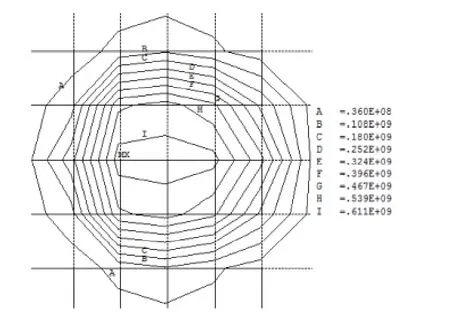
图2 轮轨接触形状

图3表示的是轮轨接触区域的等效Mises应力，车轮和钢轨的最大等效Mises应力分别为420.9 MPa和362.2 MPa。

图3 轮轨接触区域Mises应力等值线

3.2 模态计算值

结构的振动频率和振型是反映结构振动的两个重要指标，前者是从时间方面反映结构的振动特性，而后者描述的是空间特性。结构的振型是反映该结构最有可能出现的变形形式，表1给出了轮轨系统的前五阶的振动频率和对应的变形部位。

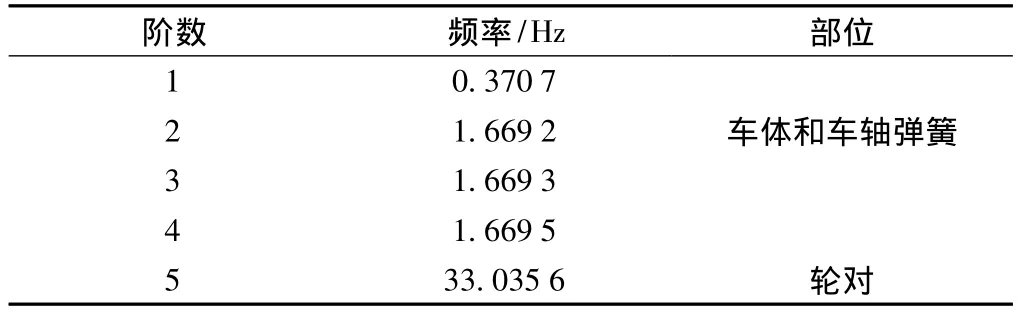
表1 振动频率

从表1中可以看出，前4阶频率都是车轴弹簧和车体的振动，其振动的频率都小于2 Hz，计算结果也表明，轮轨系统其他部件的振动频率都比较大。图4给出的是第五阶频率对应的振型图。

3.3 谱分析结果

图4 第5阶振型

由于功率谱值的变量是频率，因而可以很清楚地反映出某一量值对频率的敏感程度。谱分析的基础是模态分析，在获取结构的振动频率之后，根据式(4)计算相应初始的谱值，将其作为原始激励施加在结构的基础部分，进而就可以进行谱分析，在计算谱值的过程中进行了模态组合，并且计算了响应谱值的绝对值。

图5给出的是车体竖向位移响应功率谱，从图5可以看出来在于不同行车速度下车体竖向位移最大值对应的频率为1.669 Hz，并且当车速增大时，其谱值也相应地增大。

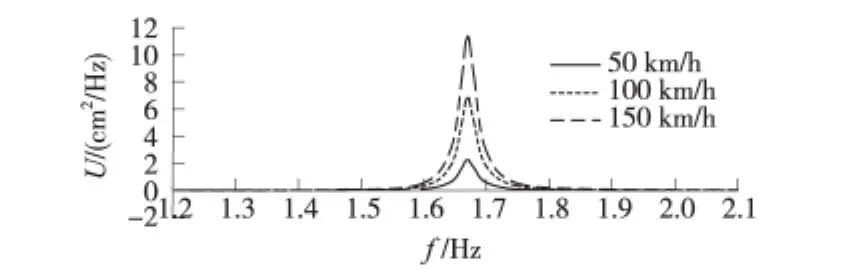
图5 车体竖向位移功率谱值

车轴和车轮底面竖向位移谱的变化规律和车体的是相似的;表2给出了轮轨系统不同部位竖向位移谱值U(cm/Hz)的最大值和相对应的频率f(Hz)。从表2可以看出，不同部位的响应谱值随着车速的增大也是逐渐增大的，车轴和车轮底部最大谱值对应的频率在不同的车速下是相同的，但车体最大反应谱对应的频率很小。

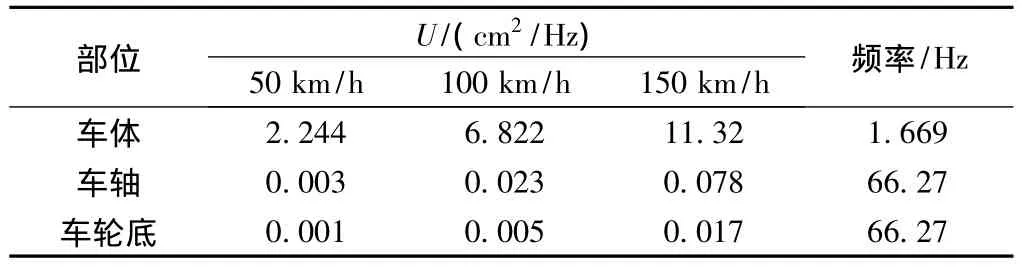
表2 最大竖向位移功率谱值

图6表示的车轮底面竖向加速度响应谱值。从图中可以看出，轮底加速度响应谱最大值在不同的车速下对应的频率为66.28 Hz，并且响应谱值随着列车速度的增大迅速增大，在频率为105.25 Hz时出现了第二个峰值，但和第一个峰值相比其谱值小很多。

图6 车轮底加速度响应谱

表3给出了不同部位的竖向加速度谱最大值A和所对应的频率f。结合表3和计算结果，对于车体而言，其竖向加速度响应谱最大峰值出现在频率为105.25 Hz的地方，而次峰值所对应的频率为1.669 Hz;对于车轴和车轮底主峰值对应的频率为66.28 Hz，次峰值对应的频率为105.25 Hz，并且加速度响应谱值都是随着车速的增加而增加的。

表3 最大加速度响应谱值

4 结论

建立了三维轮轨接触的有限元模型，进行了静力分析和动力分析，获取了轮轨接触的基本特征和系统振动时不同部位的谱值，主要结论如下。

(1)系统低阶振动频率主要是车体的振动，其频率值在2 Hz以内，车轮、转向架和车轴的振动频率较高。

(2)车体竖向位移谱主峰值对应的频率为1.669 Hz，而其加速度第一波峰值对应的频率为105.25 Hz，其频率值相差较大。

(3)对于车轴和车轮底部竖向位移和加速度响应谱最大值对应的频率分别为66.27 Hz和66.28 Hz，两者很接近。

(4)位移和加速度响应谱值随着车速的增大逐渐增大。

［1］ 翟婉明，夏禾.列车-轨道-桥梁动力相互作用理论与工程应用［M］.北京:科学出版社，2011:101.

［2］ 钱雪军.轨道不平顺的时域模拟法［J］.铁道学报，2000，22(4):94-97.

［3］ 徐磊，陈宪麦，徐伟昌，等.基于小波和Wigner-Ville分布的轨道不平顺特征识别［J］.中南大学学报，自然科学版，2013，44(8):3345-3348.

［4］ 项盼，赵岩，林家浩.轨道不平顺激励下不确定车轨耦合系统动力分析［J］.固体力学学报，2012，33(S):205-208.

［5］ 冯青松，雷晓燕，练松良.轨道随机不平顺影响下高速铁路地基动力分析模型［J］.振动工程学报，2013，26(6):927-930.

［6］ 梁波，蔡英.不平顺条件下高速铁路路基的动力分析［J］.铁道学报，1999，21(2):84-87.

［7］ 杨丽娟，丁学锋，付昌友，等.澳大利亚某矿区配套铁路重载技术选型研究［J］.铁道标准设计，2014，58(1):46-48.

［8］ 张东风.山西中南部铁路30 t轴重75 kg/m钢轨重载道岔设计研究［J］.铁道标准设计，2014，58(6):18-20.

［9］ 薛海，李永昶，刘万选.机车车辆螺旋弹簧的试验方法研究［J］.兰州交通大学学报，2013，32(4):140-142.

［10］孙训方，方孝淑，关来泰，等.材料力学［M］.北京:高等教育出版社，2009:21.

［11］常崇义.有限元轮轨滚动接触理论及其应用研究［D］.北京:中国铁道科学研究院，2010:108.

［12］任尊松.车辆系统动力学［M］.北京:中国铁道出版社，2007:170-175.

［13］刘寅华，李芾，黄运华.轨道不平顺数值模拟方法［J］.交通运输工程学报，2006，6(1):30-32.

Modal/spectrum Dynamic Response Analyses of Wheel/rail System under the Condition of Track Irregularity Based on ANSYS

WEI Yun-peng1，WU Ya-ping1，CHEN E1，DUAN Zhi-dong1，WANG Liang-bi2
(1.School of Civil Engineering，Lanzhou Jiaotong University，Lanzhou 730070，China;2.School of Mechatronic Engineering，Lanzhou Jiaotong University，Lanzhou 730070，China)

In order to analyze the dynamic responses of wheel/rail system under the condition of track irregularity，the finite element model of wheel/rail system is established based on the dynamic principle and finite element method，static and modal/spectrum analyses of wheel/rail system are carried，and basic contact characteristics of wheel/rail，displacement and acceleration response spectrum values of wheel/rail system in different parts are obtained.The results show that the maximum vertical displacement spectrum values of train body correspond to the frequency of 1.669 Hz，while the maximum acceleration spectrum values of train body correspond to the frequency of 105.25 Hz.The maximum vertical displacement and acceleration spectrum values of axle and bottom wheel correspond to the frequency of 66.27 Hz and 66.28 Hz respectively.At the same time the results also indicate that displacement and acceleration response spectrum values increase with the increase of train speed.

wheel/rail contact;Track irregularity;Power spectrum;Dynamic response;Finite element

U221

A

10.13238/j.issn.1004-2954.2015.05.011

1004-2954(2015)05-0051-03

2014-08-08;

2014-08-28

国家自然科学基金重点项目(51236003)

魏云鹏(1988—)，男，硕士研究生，E-mail:ypweiinchina@126.com。

美国轨道高低不平顺谱，其表达式为