一种新型支撑形式对钢弹簧浮置板轨道振动特性的影响

高佳颖，金 浩*，刘维宁，彭智勇

(1.绍兴文理学院土木工程学院，绍兴 312000;2.北京交通大学土木建筑工程学院，北京 100044)

一种新型支撑形式对钢弹簧浮置板轨道振动特性的影响

高佳颖1，金 浩1*，刘维宁2，彭智勇2

(1.绍兴文理学院土木工程学院，绍兴 312000;2.北京交通大学土木建筑工程学院，北京 100044)

在现有钢弹簧浮置板轨道支撑形式的基础上，提出一种全新的支撑形式。采用数值模态分析的方法，研究该种支撑形式对钢弹簧浮置板轨道振动特性的影响。分析结果表明:(1)在同等浮置板板长的条件下，本文提出的支撑形式，可以获得更低的1阶自振频率，但不改变高阶自振频率和振型;(2)浮置板板长的增加，对钢弹簧浮置板轨道的前3阶自振频率影响不大，丰富了钢弹簧浮置板轨道的高阶(弯曲)振型。本文提出的支撑形式，有利于提高钢弹簧浮置板轨道的减振能力。

支撑形式;钢弹簧浮置板轨道;模态分析;自振频率;振型

随着城市轨道交通的大量投入运营，由轮轨耦合振动引起的环境振动问题越来越受到关注［1-2］。相比于其他轨道减振形式［3-5］，定义为高等减振措施的钢弹簧浮置板轨道，其从进入中国轨道交通市场起，在地铁减振方面一直扮演着重要角色。

目前，钢弹簧浮置板轨道的研究方法，主要可归纳为理论解析、数值模拟(自编程序或者商业软件)以及测试(实验室或者现场)。如郭亚娟等［6］利用ANSYS软件，建立了浮置板轨道系统的有限元模型。采用Newmark时间积分方法，模拟了列车荷载作用下浮置板轨道结构的瞬态响应。丁德云等［7］应用 MIDAS/GTS软件，对浮置板轨道进行了三维模态分析。谷爱军等［8］建立了三维钢弹簧浮置板轨道有限元模型，针对不同设计参数和激振频率，研究了该轨道结构的动力传递特性和隔振效率。丁德云等［9］采用 MIDAS/GTS软件对钢弹簧浮置板轨道进行了动力特性研究。刘维宁等［10］利用北京交通大学轨道减振与振动控制试验室进行了钢弹簧浮置板轨道低频特征测试，研究了钢弹簧浮置板轨道弹簧刚度和支承间距等参数变化对低频振动的影响，并比较了钢弹簧浮置板轨道和普通轨道的低频减振效果。肖安鑫等［11］通过不同钢弹簧浮置板轨道地段车内噪声的对比测试，分析了钢弹簧浮置板轨道对车内噪声的影响。韦红亮等［12］分别采用有限元和现场试验方法，从时频域角度对高架钢弹簧浮置板轨道结构的减振特性进行了分析。蒋崇达等［13］利用ANSYS软件建立了钢弹簧浮置板轨道系统的双层梁动力学模型，通过瞬态分析模拟了列车移动荷载通过钢弹簧浮置板轨道时的动力响应。韩朝霞等［14］为研究道岔区钢弹簧浮置板轨道结构的受力特性，建立了道岔区钢弹簧浮置板轨道的三维有限元模型。

在以上研究的基础上，探讨了一种全新的液压弹簧阻尼器布设形式。通过数值模态分析，比较分析了新型液压弹簧阻尼器布设形式对钢弹簧浮置板轨道振动特性的影响。

1 支撑形式

以位于“北京交通大学轨道减振与控制实验室”的钢弹簧浮置板轨道为例(如图1所示，以下简称SSFS-1)，浮置板长6 000 mm，截面为3 500 mm×450 mm，液压弹簧阻尼器布设在浮置板两侧，相邻间距1 200 mm，如图2所示。

图1 位于“北京交通大学轨道减振与控制实验室”的钢弹簧浮置板轨道

在现有液压弹簧阻尼器布设形式的基础上，设计了一种液压弹簧阻尼器全新布设形式的钢弹簧浮置板轨道(以下简称SSFS-2)。将图2(a)中的液压弹簧阻尼器#2、#4、#7、#9去掉，在对应横断面中部设置液压弹簧阻尼器#N2和#N4。新型液压弹簧阻尼器布设形式如图3所示。

为全面研究此种布设形式对钢弹簧浮置板轨道自振特性的影响，进一步考虑了浮置板板长的影响。在SSFS-2的基础上，以2 400 mm为基本单元长度，设计了钢弹簧浮置板轨道SSFS-3(板长8 400 mm，如图4所示)和SSFS-4(板长10 800 mm，如图5所示)。

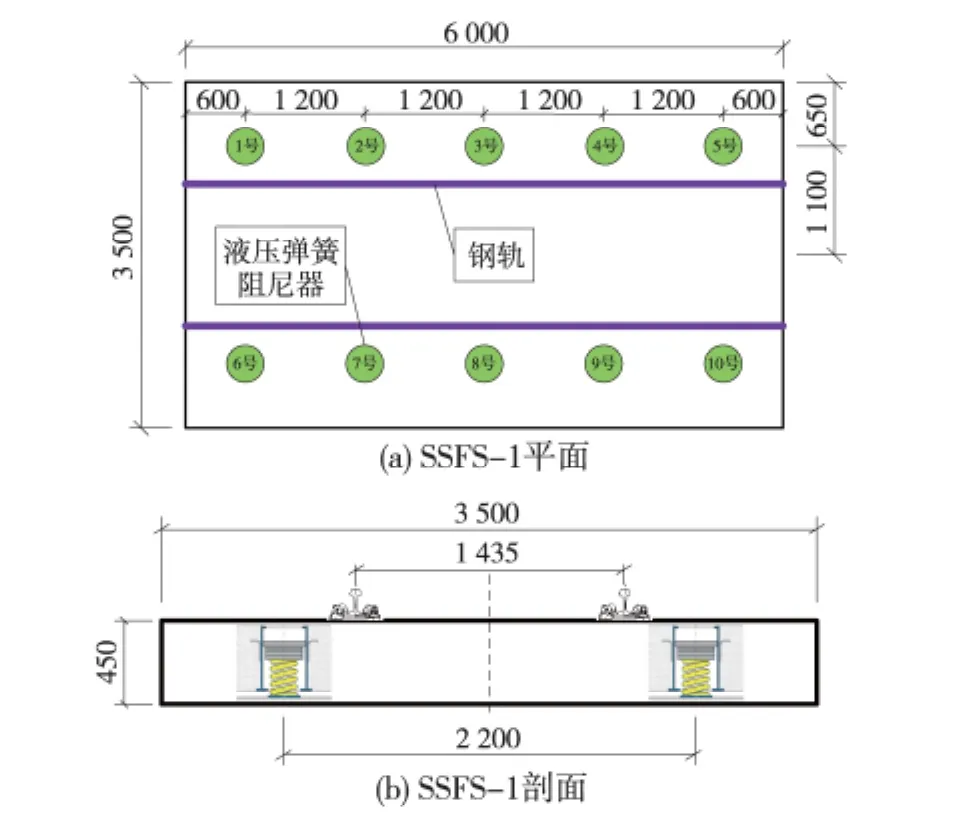
图2 SSFS-1结构尺寸及液压弹簧阻尼器位置(单位:mm)

图3 SSFS-2结构尺寸及液压弹簧阻尼器位置(单位:mm)

图4 SSFS-3平面(单位:mm)

图5 SSFS-4平面(单位:mm)

2 数值模型

2.1 模态分析原理

特征频率和结构振动模态描述了结构在自由振动下的频率特征和振动特点。一个无阻尼自由振动系统的特征方程为

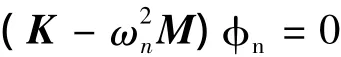
其中，K为结构的刚度矩阵;M为结构的质量矩阵;ωn为第n个振型的周期;φn为第n个振型的振型向量。

2.2 有限元模型

SSFS-1、SSFS-2、SSFS-3、SSFS-4 几何尺寸如图2～图5所示。浮置板的弹性模量为31 GPa，泊松比为0.2，密度为2 500 kg/m3。液压弹簧阻尼器采用线弹簧进行模拟，竖向刚度选用5.3 MN/m。典型(SSFS-1)有限元模型见图6。

图6 SSFS-1有限元模型

3 结果分析

3.1 振型分析

通过对 SSFS-1、SSFS-2、SSFS-3、SSFS-4 进行模态分析，得到4种钢弹簧浮置板轨道的前8阶振型，如表1所示。本文采用的笛卡尔坐标系如图6所示。

对比 SSFS-1、SSFS-2、SSFS-3、SSFS-4 的前 3 阶振型，可以发现:

(1)SSFS-1的1阶振型为绕X轴的转动，改变液压弹簧阻尼器位置后，SSFS-2、SSFS-3、SSFS-4的1阶振型为绕Z轴的转动;

(2)SSFS-1、SSFS-2、SSFS-3、SSFS-4 的 2 阶振型主要为Y轴的平动，改变液压弹簧阻尼的位置，对钢弹簧浮置板轨道2阶振型没有影响;

(3)SSFS-1的3阶振型为绕Y轴的转动，改变液压弹簧阻尼器位置后，SSFS-2、SSFS-3、SSFS-4的1阶振型为绕X轴的转动。

第4、第5 阶振型，SSFS-2、SSFS-3、SSFS-4 和SSFS-1相同，分别为弯曲振型和扭转振型。

第6～第8阶振型，SSFS-2和SSFS-1具有相同的振型;SSFS-3和SSFS-4相比于SSFS-2和SSFS-1，振型更加丰富(主要表现为弯曲振型增多)。

表1 SSFS-1、SSFS-2、SSFS-3、SSFS-4 的1 ～8 阶振型

3.2 自振频率分析

SSFS-1、SSFS-2、SSFS-3、SSFS-4 前 8 阶自振频率如表2所示，自振频率变化趋势如图7所示。从表2和图7可以得出如下结论。

表2 SSFS-1、SSFS-2、SSFS-3、SSFS-4的1～8阶自振频率 Hz

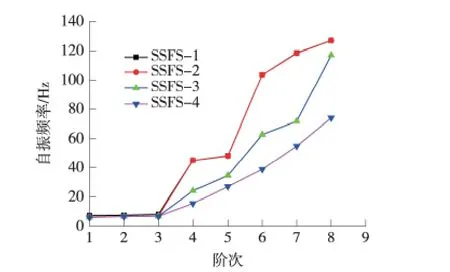
图7 SSFS-1、SSFS-2、SSFS-3、SSFS-4 的自振频率

(1)对比SSFS-1和SSFS-2，主要是前3阶自振频率有变化，第4阶及以后的自振频率基本没有改变。这说明，前3阶的自振频率变化，由液压弹簧阻尼器布设形式发生改变引起。采用新的布设形式，降低了钢弹簧浮置板轨道的1阶自振频率，有利于提高钢弹簧浮置板轨道的减振性能。

(2)对比SSFS-2、SSFS-3以及SSFS-4，发现前3阶自振频率变化不明显，从第4阶开始，自振频率发生较大变化。随着板长的增大，第4阶之后的共振频率随之减小。

4 结语

本文提出了一种全新的液压弹簧阻尼器布设形式，通过钢弹簧浮置板轨道的模态分析，得出以下结论。

(1)本文提出的液压弹簧阻尼器布设形式，在同等浮置板板长的条件下，可以获得更低的1阶自振频率，但不改变高阶自振频率和振型。此种液压弹簧阻尼器布设形式，有利于提高钢弹簧浮置板轨道的减振能力。

(2)浮置板板长的增加，对钢弹簧浮置板轨道的前3阶自振频率影响不大，主要丰富了钢弹簧浮置板轨道的高阶振型。

［1］ Gupta S，Liu W F，Liu W N，et al.Prediction of vibrations induced by underground railway traffic in Beijing［J］.Journal of Sound and Vibration，2008，310(3):608-630.

［2］ 李克飞，韩志伟，刘维宁，等.基于现场锤击试验的地铁轨道振动特性分析及参数研究［J］.铁道标准设计，2014(2):12-16.

［3］ 马娜，李成辉.梯形轨枕竖向振动模态分析［J］.工程力学，2010，27(5):247-249.

［4］ 金浩，刘维宁，王文斌.梯式轨枕轨道模态试验分析［J］.工程力学，2013，30(3):459-463.

［5］ 金浩，刘维宁.蚁群算法耦合LS-DYNA梯式轨枕轨道动力特性优化［J］.振动与冲击，2013，32(2):24-28.

［6］ 郭亚娟，杨绍普，郭文武.钢弹簧浮置板轨道结构的动力特性分析［J］. 振动测试与诊断，2006，26(2):146-150.

［7］ 丁德云，刘维宁，张宝才，等.浮置板轨道的模态分析［J］.铁道学报，2008，30(3):61-64.

［8］ 谷爱军，张宏亮.钢弹簧浮置板轨道结构在不同频段的隔振效率［J］.噪声与振动控制，2009，29(1):39-42.

［9］ 丁德云，刘维宁，李克飞，等.钢弹簧浮置板轨道参数研究［J］.中国铁道科学，2011，32(1):30-35.

［10］刘维宁，丁德云，李克飞，等.钢弹簧浮置板轨道低频特征试验研究［J］.土木工程学报，2011，44(8):118-125.

［11］肖安鑫，田野.钢弹簧浮置板轨道对车内噪声影响的实测与分析［J］.噪声与振动控制，2012，32(1):51-54.

［12］韦红亮，练松良，周宇.高架钢弹簧浮置板轨道减振特性分析［J］.同济大学学报:自然科学版，2012，40(9):1342-1348.

［13］蒋崇达，雷晓燕.城市轨道交通钢弹簧浮置板轨道动力特性分析［J］.城市轨道交通研究，2013，16(3):34-41.

［14］韩朝霞，孙方遒，谷爱军.道岔区钢弹簧浮置板轨道结构静力分析［J］.铁道标准设计，2014(1):1-5.

Research on Effects of a New Supporting Form on Vibration Characteristics of Steel Spring Floating Slab Track

GAO Jia-ying1，JIN Hao1，LIU Wei-ning2，PENG Zhi-yong2
(1.College of Civil Engineering，Shaoxing University，Shaoxing 312000，China;2.School of Civil Engineering，Beijing Jiaotong University，Beijing 100044，China)

A new supporting form for the steel spring floating slab track is proposed in this paper based on present supporting forms.The effects of this supporting form on vibration characteristics of the steel spring floating slab track are analyzed with numerical model analysis method.The results show that:(1)The steel spring floating slab track supported by the new form style has lower 1storder natural frequency than that of the present steel spring floating slab track with same lab length without changing high order natural frequencies and vibration mode.(2)Natural frequencies of first three orders are less affected by the slab length，and the high order(bending)vibration mode of the steel spring floating slab track is enriched.Therefore，the supporting form proposed in this paper helps improve the ability to reduce vibration of the steel spring floating slab track.

Supporting form;Steel spring floating slab track;Modal analysis;Natural frequency;Vibration mode

U231

A

10.13238/j.issn.1004-2954.2015.05.008

1004-2954(2015)05-0037-03

2014-08-06;

2014-08-16

国家自然科学基金项目(51008017)

金 浩(1986—)，男，讲师，博士，E-mail:zhujijinhao@gmail.com。