引出向量组线性无关概念的方法探究

吴世玕，杜红霞

(1.江西理工大学 理学院，江西 赣州341000；2.江西理工大学 机电学院，江西 赣州 341000)

线性代数学时少，内容比较抽象.很多教材在处理向量组线性相关性问题时，都是按照“概念-定理-例题-习题”这种顺序编写的，缺少概念的实际模型，与中学数学联系得也较少，几乎不讲应用实例.线性相关、线性无关这部分内容，学生学起来总觉得抽象，定理较多，难于学懂.究竟应该怎么教授这部分内容，笔者作了一番思考，从n次多项式的表达，向量分解惟一性，坐标系的构建，线性方程组中多余方程四个学生熟悉的模型中提炼出线性相关与线性无关的概念，学生易于接受，学起来也更有兴趣.

1 用n次多项式结构引出向量组线性无关概念

n次多项式是学生们在中学就已经熟悉的内容，用它引出线性相关与线性无关概念，学生们听起来就会觉得更轻松，有似曾相识的感觉.

记实系数n次多项式的全体为集合V，则任何一个n次多项式都可以用给定的n+1个最简单的多项式1,x,x2,x3,…,xn，通过多项式相加及实数与多项式相乘两种运算(称为多项式的线性运算)来表达.且从1,x,x2,x3,…,xn中无论去掉哪一个，都无法用剩下的n个多项式线性表达出所有的n次多项式.换言之，要想用线性运算表达出所有实系数 次多项式，有这n+1个最简单的多项式1,x,x2,x3,…,xn就足够了，且少一个都不行.

那么，多项式组1,x,x2,x3,…,xn有何性质？多项式组1,x,x2,x3,…,xn中每一个多项式都不能由其余n个多项式线性表示.称满足这个性质的多项式组是线性无关的.如果记多项式系数，按顺序组成一个n+1维向量.则研究n次多项式问题等价于研究n+1维向量的问题.对于只含有一个向量的向量组，若这个向量不是零向量，则称这个向量组是线性无关的.如果m≥2 ，向量组α1,α2,…,αm中的任何一个向量都不可能由这个向量组的其它向量线性表示，则称这个向量组线性无关.按这样理解，向量组α1,α2,…,αm线性无关，就是向量组中的向量之间没有任何线性关系，“谁也线性表示不了谁”.从线性表示的意义来说，它们彼此是独立的，这正是线性无关的含义.

容易证明，m≥2时，α1,α2,…,αm线性无关的充要条件是，零向量用α1,α2,…,αm线性表示时，表示法是惟一的，系数只能全为零.

由上面多项式的讨论知，任何一个n次多项式都可以用1,x,x2,x3,…,xn线性表示.从1,x,x2,x3,…,xn中除去任何一个，都不足以线性表示所有的n次多项式.若α1,α2,…,αm是n维向量组A的部分向量组，向量组A中任何一个向量都可由α1,α2,…,αr线性表示，且从α1,α2,…,αr中去掉任何一个向量，都不足以线性表示A中所有向量(由此易证，去掉的那个向量不能由剩下的r-1个向量线性表示，由所去掉向量的任意性，从而知α1,α2,…,αr一定是线性无关的)，称α1,α2,…,αr为向量组A的最大无关组.

2 用向量分解惟一性引出向量组线性无关概念

以三维向量空间R3为例，在空间解析几何中，我们已经学习了向量坐标概念.任何一个三维向量α=(α1α2α3)都可由基本单位向量组ε1=(1 0 0),ε2=(0 1 0),ε3=(0 0 1)线性表示，且线性表示方法是惟一的，表示的系数就是向量的分量.正因为线性表示方法是惟一的，才能合理地定义向量坐标概念.

这里有一个向量分解惟一性的问题.设向量β能由向量组α1,α2,…,αm线性表示，则称向量β可分解为向量组α1,α2,…,αm的线性组合.感兴趣的问题是：向量β分解为向量组α1,α2,…,αm的线性组合时，分解方法是否惟一.我们往往要研究很多向量分解的惟一性.比如，向量空间R3中任一向量可否分解为向量组α1,α2,…,αm的线性组合，且分解是惟一的？向量空间R3中有无穷多个向量，如果一个一个地检查，那是不可能的.是否有一种简洁的办法呢？可以证明，如果向量β能分解为向量组α1,α2,…,αm的线性组合，则向量β分解为向量组α1,α2,…,αm的线性组合方法是惟一的，等价于零向量分解为向量组α1,α2,…,αm的线性组合方法是惟一的，即分解系数只能全为零.由此给出向量组线性无关的定义.

定义1n维向量组α1,α2,…,αm线性无关，指的是零向量分解为α1,α2,…,αm的线性组合时，分解方法是惟一的，即分解系数只能全为零.

如果零向量分解为α1,α2,…,αm的线性组合时，分解方法不是惟一的，即分解系数可以不全为零，则称向量组α1,α2,…,αm线性相关.

进一步的问题是，给定n维向量组A，若A中含有非零向量，是否可能从A中选出最少个数的向量α1,α2,…,αr，使得A中任何一个向量β都能分解为α1,α2,…,αr的线性组合(即向量组A与向量组α1,α2,…,αr等价).

如果A中只有一个向量，那这个问题就太简单了.问题是A中可能有很多向量，甚至无穷多个向量.我们先来看一下α1,α2,…,αr应该具有什么性质.

(1)α1,α2,…,αr是线性无关的.否则α1,α2,…,αr中至少有一个向量可由其它r-1个向量线性表示，从而A中向量都可以由这r-1个向量线性表示，与“个数最少”的要求不符.

(2)向量组A中任何r+1个向量是线性相关的(如果A中有r+1个向量).事实上，若A中部分向量组β1,β2,…,βr+1线性无关，由于β1,β2,…,βr+1可由α1,α2,…,αr线性表示，从而r+1≤r，产生矛盾.

(1)和(2)也表明向量组α1,α2,…,αr与向量组A等价.

由于n+1个n维向量构成的向量组总是线性相关的，因此，这种部分向量组α1,α2,…,αr是一定存在的.称选出来的最少个数的部分向量组α1,α2,…,αr为向量组A的最大无关组.

(1)和(2)也表明，向量组A的最大无关组中所含向量个数是惟一确定的(否则，若向量组A有两个最大无关组，分别含有r个和t个向量，则由(1)和(2)知，r≤t，t≤r,从而r=t).称向量组A的最大无关组中所含向量的个数为向量组A的秩.

3 用坐标系的构建引出向量组线性无关概念

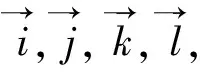
定义2n维向量组α1,α2,…,αm线性无关，指的是零向量分解为α1,α2,…,αm的线性组合时，分解方法是惟一的，即分解系数只能全为零.

若α1,α2,…,αr是向量组A的一个线性无关的部分向量组，且A中任何一个向量都可由α1,α2,…,αr线性表示，则称α1,α2,…,αr是A的一个最大无关组.

在构建坐标系时，就是要选择空间中的最大无关组作为坐标轴方向的向量.当然，互相正交的直线上的向量，是线性无关的.在三维空间中，能且只能作出三条互相正交的坐标轴，也就是说，空间的最大无关组中含有三个向量.

4 用多余方程引出向量组线性无关概念

如果一个方程组中有某个方程是其余方程的线性组合(通过方程两端相加，数乘方程两端两种运算将方程组合起来)，就称这个方程组中的方程线性相关.如果一个方程组中的每个方程都不是其余方程的线性组合，就称这些方程线性无关.换言之，在线性运算意义下，方程组中每个方程都是独立的，与其它的方程无关.

在一个方程组中，若某个方程是其余方程的线性组合，则删去这个方程后所得方程组与原方程组同解.将这件事情一直进行下去，最后必将得到与原方程组同解的方程组，所剩下的方程是线性无关的.

由于线性方程组中，起关键作用的是系数和右边常数项.仿照上面说法，我们给出向量组的线性相关与线性无关的概念.

定义3 给定向量组A，若A中含有两个或两个以上向量，且其中至少有一个向量是其它向量的线性组合，则称向量组A线性相关;若A中每个向量都不是其它向量的线性组合，则称向量组A线性无关.若A中只有一个向量α，则规定，当且仅当α=0时，向量组A线性相关.