几何参数对环肋圆柱壳肋骨侧向稳定性的影响

吴　梵1，王　金1，刘　勇2，滑　林11海军工程大学舰船工程系，湖北武汉430033 2武汉第二船舶设计研究所，湖北武汉430205

几何参数对环肋圆柱壳肋骨侧向稳定性的影响

吴梵1，王金1，刘勇2，滑林1
1海军工程大学舰船工程系，湖北武汉430033 2武汉第二船舶设计研究所，湖北武汉430205

环肋圆柱壳一般通过在周向布置肋骨来提高其稳定性，肋骨的侧向稳定性对环肋圆柱壳整体稳定性具有重要意义。根据肋骨的侧向失稳机理，利用肋骨侧向稳定性解析解公式，在理论分析和实例计算的基础上，分析了环肋圆柱壳肋骨的几何参数与肋骨侧向失稳临界压力的关系，研究了各参数对肋骨侧向失稳临界压力的贡献值，最后得到了几何参数对肋骨侧向稳定性的影响规律。

环肋圆柱壳；外压力；屈曲；侧向稳定性；几何参数；贡献值

0　引言

环肋圆柱壳是潜水器耐压结构的基本形式，随着下潜深度的增大，对环肋圆柱壳结构强度和稳定性的要求越来越高，肋骨尺寸会加大，出现肋骨侧向失稳破坏的可能性增大。肋骨的侧向失稳可能引起环肋圆柱壳的总体失稳，因此研究肋骨侧向稳定性具有重要意义。肋骨的几何参数是影响肋骨侧向稳定性的基本因素，因此研究几何参数对肋骨侧向稳定性的影响规律是避免肋骨侧向失稳的基础。

环肋圆柱壳肋骨侧向失稳［1］可描述为：在静水外压力作用下，肋骨绕着与圆柱壳连接点发生侧向弯扭变形，肋骨的侧向位移大于圆柱壳的径向位移，且肋骨腹板在高度方向存在1/4个波，在周向存在4～8个波，翼板绕着腹板产生扭转变形。

对于肋骨稳定性计算方法的研究，郭日修［2］将带板的肋骨提取出来，取名为肋骨环，由于肋骨在制造时存在圆度偏差，该肋骨环可以看成是一个受偏心压力的开口薄壁［3］环形梁［4］，环形梁在外载荷作用下，发生屈曲扭转变形，产生肋骨侧向失稳。Kendrick［5］认为，对肋骨尺寸进行设计，可有效防止因肋骨侧向失稳而造成的舱段破坏。Kennard［6］早期曾研究肋骨侧向倾斜，认为肋骨固支在壳板上，并基于此提出一种比较精确的算法，以确定肋骨的弹性倾斜应力。Adamchack［7］利用能量法，提出了一种考虑肋骨腹板变形影响的算法。

本文将基于肋骨侧向失稳的机理，寻找较为精确的肋骨侧向失稳的解析解公式，并据此系统地研究肋骨基本几何参数和中间几何参数对肋骨侧向稳定性的影响，分析各参数对肋骨侧向稳定性的贡献值，最后得出几何参数对肋骨侧向稳定性的影响规律，以期为大潜深潜水器结构设计提供技术指导。

1　肋骨尺寸影响研究

1.1解析解分析

冯泽·米赛斯假设肋骨没有偏离地支撑着壳板，并提出了弹性肋间壳板屈曲压力pm的公式［1］:

式中：E为弹性模量；t为壳板厚度；R为平均半径；L为壳板的无支撑长度；ν为泊松比；n为周向失稳波数。

早期的规范BS5500［1］对肋骨侧向倾斜制定了相应的设计标准，该标准相对保守，在计算肋骨侧向失稳应力时，忽略了壳板提供的转动约束，要求肋骨侧向失稳应力σt应该大于肋骨材料屈服应力σs，即

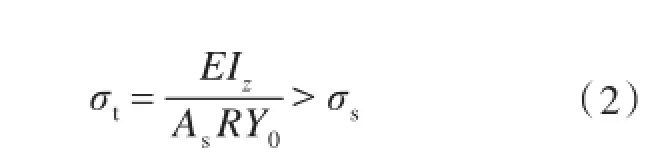
式中：IZ是对称轴截面惯性矩；As是肋骨截面面积；Y0为肋骨型心高度。

Adam chack［7］利用能量法，提出了一种考虑腹板变形影响的算法，计算肋骨侧向失稳应力如下：

由于系数k1~k6与肋骨倾斜应力相关，Morandi等［1］采用隐函数解法，得到一个更适合手算和可靠性分析的公式：

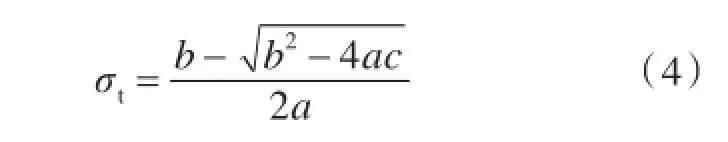
式中，pt为肋骨侧向失稳临界压力。

式（4）适用于正圆形的T型肋骨，并假设肋骨与壳板刚性连接，其中：

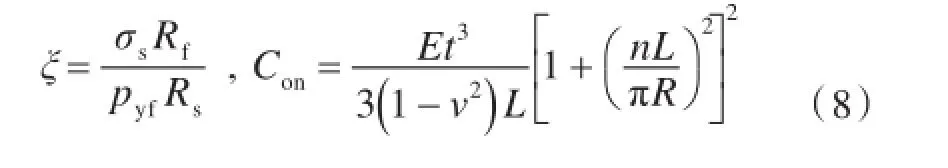
Faulkner［8］推导出了肋骨屈服主要应力的公式

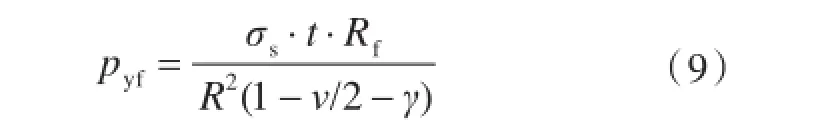
上式中：G为剪切模量；J为扭转惯性矩；Γ1为纵向翘曲常数；Γ2为横向翘曲常数；d为翼板中心高度；ξ为比例系数；Con为稳定的转动约束；Ips为剪切中心极惯性矩；pyf为肋骨屈服压力；Rs为肋骨型心半径；Rf为翼缘半径；tw和dw分别为肋骨腹板厚度和高度；tf和bf分别为肋骨翼板厚度和高度。

文献［1］给出了一个算例，相关数据如表1所示，其中Web代表腹板，Flange代表翼板。

表1　尺寸参数Tab.1 Dim ension param eters

将表1中数据代入解析解公式得到失稳压力与周向波数的关系，如图1所示。分析环肋圆柱壳失稳特征可知：当肋骨侧向失稳临界压力pm远小于壳板失稳临界压力pt，即pm＜＜pt时（C区域），环肋圆柱壳主要发生壳板失稳；当pt＜pm时（A区域），环肋圆柱壳主要发生肋骨侧向失稳；当pt与pm相近时（B区域），环肋圆柱壳主要发生混合失稳。对于环肋圆柱壳的初步设计，为了避免肋骨发生侧向失稳，在pt＜pm的范围内找到pt的极小值pt-min，作为肋骨侧向失稳的临界压力，并使相应的肋骨侧向失稳临界应力大于肋骨材料屈服应力，即σt＞σs，这样就可以保证不发生肋骨侧向失稳。基于这一思想，本文在上述解析解公式的基础上，通过编写计算程序，采用单一变量法，研究了几何参数对肋骨侧向稳定性的影响规律。

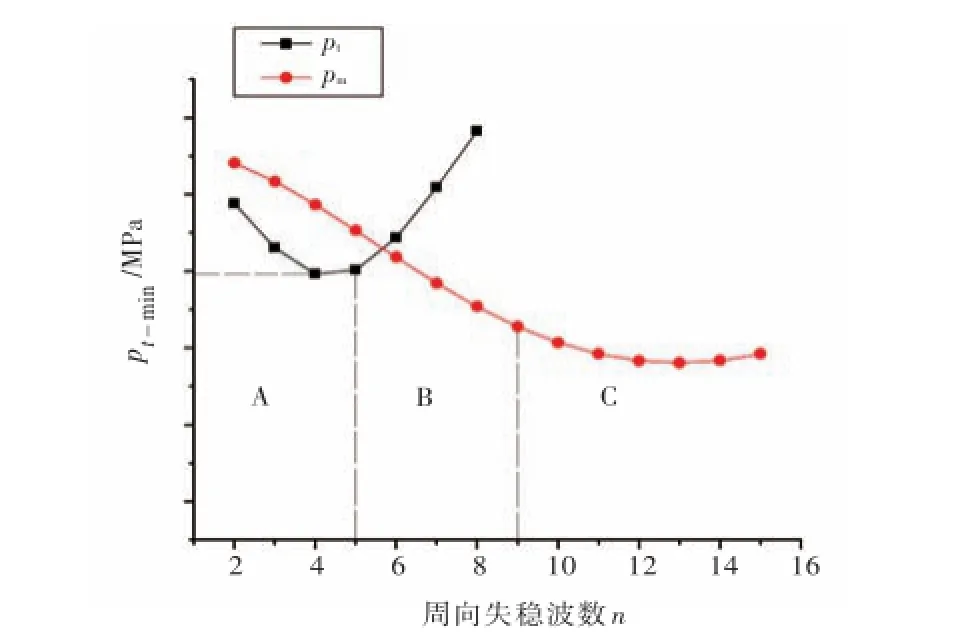
图1　压力与周向失稳波数关系图Fig.1 Variation ofelastic tripping pressurewith respect to circum ferentialnumberofwaves

1.2确定影响参数

通过对解析解分析，本文将影响肋骨侧向稳定性的几何参数分为两类，一类是肋骨的基本几何参数：肋骨腹板高度dw，肋骨腹板厚度tw，肋骨翼板宽度bf，肋骨翼板厚度tf；另一类是肋骨（不计及带板）的中间几何参数：型心高度Y0、剪切中心极惯性矩Ips、对称轴截面惯性矩IZ、扭转惯性矩J、纵向翘曲常数Γ1、横向翘曲常数Γ2。型心高度、剪切中心极惯性矩、对称轴截面惯性矩和扭转惯性矩均是肋骨的基本属性，且由肋骨基本几何参数决定，具有一定代表性；薄壁杆件如工字梁在承受扭转时将出现截面翘曲，此时结构的扭转变形必须考虑翘曲的影响。因此，对于环肋圆柱壳内置的T型肋骨，本文通过研究上述中间参数来研究其与肋骨侧向稳定性的规律。

肋骨中间几何参数的计算公式为（参数J，Γ1和Γ2见式（8））：

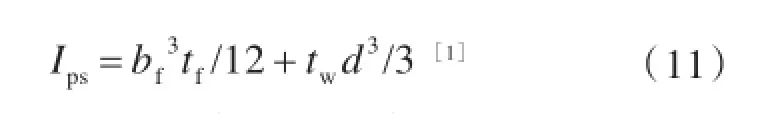
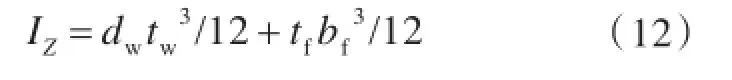
本文首先研究环肋圆柱壳基本几何参数对肋骨侧向稳定性的影响规律，然后进一步研究中间几何参数对肋骨侧向稳定性的影响规律。

2　几何参数影响研究

为了更准确地研究几何参数对肋骨侧向稳定性的影响规律，下面采用统一的算例，具体数据如下：环肋圆柱壳材料的屈服极限为785MPa，计算压力为6.62 MPa，弹性模量E=2.0×105MPa［9］，肋骨的基本几何参数为：⊥，圆柱壳的基本尺寸参数见表2。

2.1基本几何参数影响研究

通过MATLAB软件编写计算程序，采用单一变量法，分析肋骨基本几何参数对肋骨侧向稳定性的影响规律，得到影响曲线如图2～图5所示。

图2　腹板高度对侧向失稳临界压力的影响规律Fig.2 Influence of web depth on elastic tripping pressure

由图2可以得出，肋骨侧向失稳理论临界压力与dw呈负相关，随其增大而减小。这是因为，在研究肋骨侧向稳定性的问题时，首先假设壳板是稳定的，并考虑壳板对肋骨的转动约束，当dw增大时，肋骨的腹板稳定性降低，且壳板对肋骨的转动约束减弱，肋骨抵抗侧向失稳的能力减弱。所以降低dw有利于提高肋骨的侧向稳定性。

由图3～图5可以得出，肋骨侧向失稳理论临界压力与tw，bf和tf呈正相关，随其增大而增大。分析其侧向失稳机理可知:当tw变大时，肋骨的腹板稳定性增强，肋骨抵抗侧向失稳的能力增强；肋骨腹板不仅受到壳板的约束，而且受到翼板的约束，当bf变大时，肋骨翼板对腹板的约束增强，肋骨抵抗侧向失稳的能力随之增强；当tf变大时，肋骨翼板对腹板的约束增强，肋骨抵抗侧向失稳的能力随之增强。所以增大tw，bf和tf有利于提高肋骨的侧向稳定性。

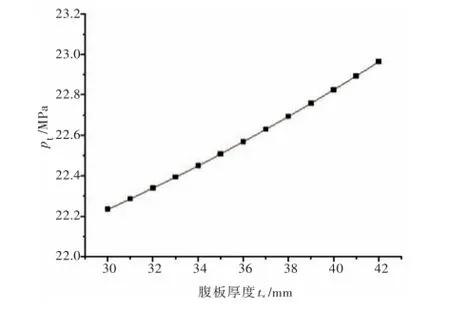
图3　腹板厚度对侧向失稳临界压力的影响规律Fig.3 Influence ofweb thickness on elastic tripping pressure

图4　翼板宽度对侧向失稳临界压力的影响规律Fig.4 Influence of flange breadth on elastic tripping pressure

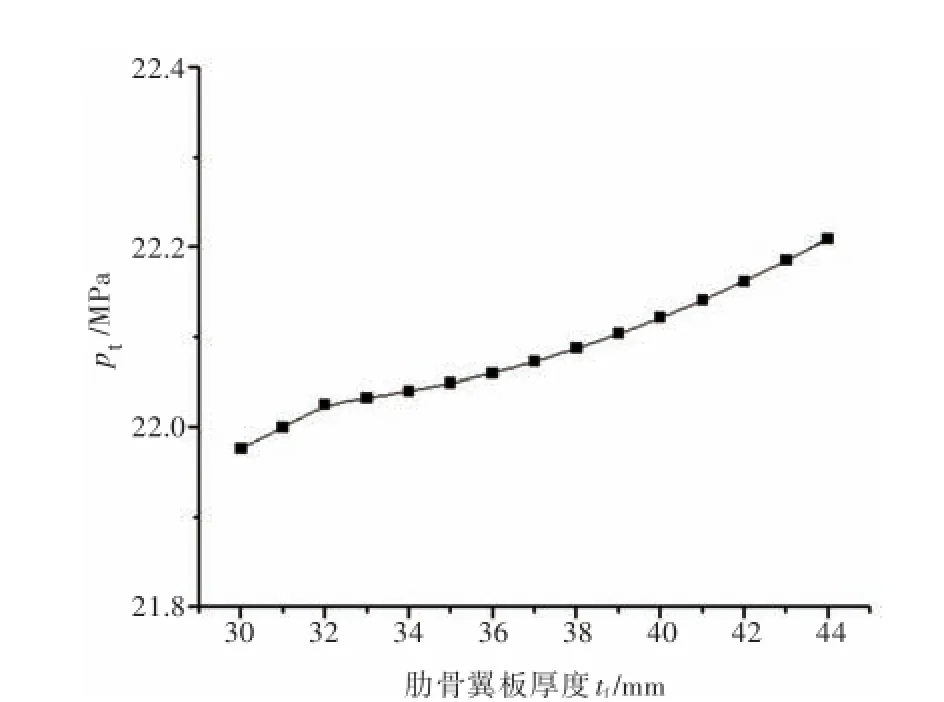
图5　翼板厚度对侧向失稳临界压力的影响规律Fig.5 Influence of flange thicknesson elastic tripping pressure

2.2中间几何参数影响研究

通过对肋骨侧向失稳临界压力解析解进行分析，探究肋骨型心高Y0、剪切中心极惯性矩Ips、对称轴截面惯性矩IZ、扭转惯性矩J、纵向翘曲常数Γ1和横向翘曲常数Γ2对肋骨侧向失稳临界压力的影响规律。在研究过程中，将肋骨尺寸参数视为常数，将中间几何参数作为相互独立的自变量，来研究单一参数的变化对肋骨侧向失稳临界压力pt的影响规律，得到影响曲线如图6～图11所示。

图6　型心高对肋骨侧向失稳临界压力的影响规律Fig.6 Influence ofheightof centroid on elastic tripping pressure

图7　剪切中心极惯性矩对侧向失稳临界压力Ips的影响规律Fig.7 Influence of section polarmomentsof inertia in relation to shear centre on elastic tripping pressure

由图6和图7可以得出，pt与Y0，Ips呈负相关，随其增大而减小，所以减小Y0和Ips有利于提高肋骨的侧向稳定性。

由图8～图11可以得出，pt与IZ，J，Γ1，Γ2呈正相关，随其增大而增大。分析其侧向失稳机理可知：当IZ增大时，肋骨的弯曲刚度增大，肋骨抵抗侧向倾斜的能力增强；当J增大时，肋骨的扭转刚度增大，肋骨抵抗扭转的能力增强；当Γ1增大时，肋骨的纵向翘曲常数刚度增大，肋骨抵抗纵向翘曲常数的能力增强；当Γ2增大时，肋骨的横向翘曲常数刚度增大，肋骨抵抗横向翘曲常数的能力增强。所以增大IZ，J，Γ1和Γ2均有利于提高肋骨的侧向稳定性。

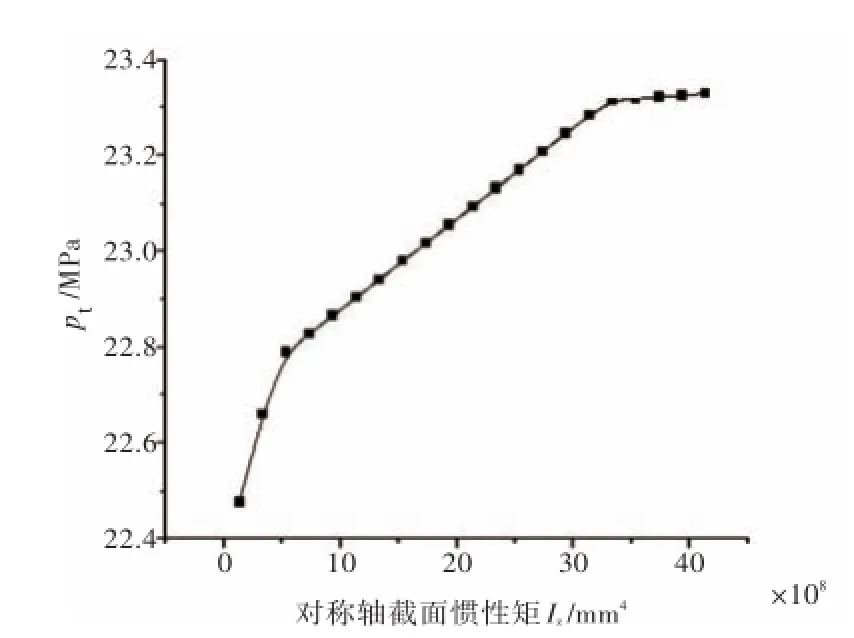
图8　对称轴截面惯性矩对侧向失稳临界压力的影响规律Fig.8Influenceofsectionmomentofinertiaaboutsymmetry axisonelastictrippingpressure

图9　扭转惯性矩对肋骨侧向失稳临界压力的影响规律Fig.9Influenceoftorsionalmomentofinertiaonelastic trippingpressure

图10　纵向翘曲常数对侧向失稳临界压力的影响规律Fig.10Influenceoflongitudinalwarpingonelastictrippingpressure

图11　横向翘曲常数对侧向失稳临界压力的影响规律Fig.11Influenceoftransversewarpingonelastictripping pressure

3　各参数贡献值分析

基于上述几何参数对肋骨侧向稳定性的影响规律，进一步确定每一个参数对肋骨侧向失稳临界压力的贡献值，尤其在工程常见肋骨尺寸的范围内，量化各参数对肋骨侧向失稳临界压力的贡献值，为结构设计提供指导是很具有工程意义的。由于肋骨侧向失稳临界压力解析解是一个多参数，即肋骨4个基本几何参数以及由它们组合的6个中间几何参数共同影响输出量pt的解析式，为此有必要明确各参数对最终输出变量pt的贡献值，以便找出最重要的参数，为工程应用提供参考。

以多元二次方程为例，对贡献值分析步骤进行简要介绍。

第1步，根据样本点建立四元二次回归模型：

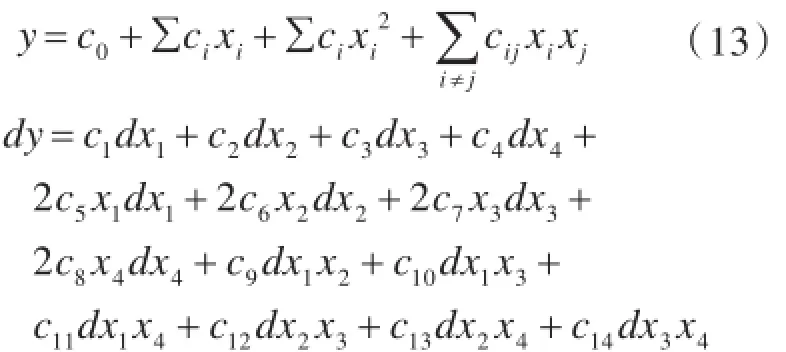
x1，x2，x3，x4线性项的主效应为：

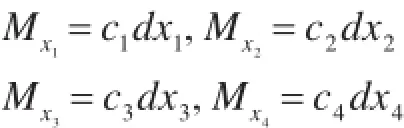
x1，x2，x3，x4二阶项的主效应为：

其中：dx=max(x)-min(x)，x=[max(x)+min(x)]/2 x1-x2交互效应为：

第2步，将输入变量归一化到［-1，+1］，然后用最小二乘法拟合，得到变量的拟合系数Si，以公平地反映出输入变量对输出量的贡献值。

归一化的计算公式为

式中：yi为归一化后的参数值；xi为归一化前的参数值。

第3步，将归一化后模型系数Si转化为贡献率百分比即得到变量对输出量的贡献值。计算方法为

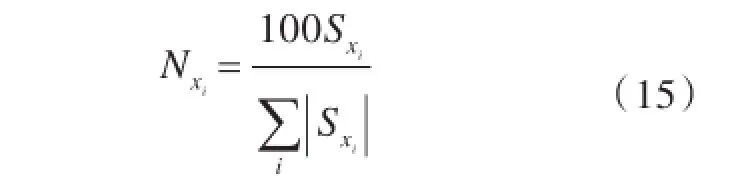
考虑到参数及参数之间的关系比较复杂，所以贡献值分析的计算量比较大，为此借助Isight软件进行贡献值分析，得出各个参数对目标函数pt的影响，从而找出影响肋骨侧向失稳临界压力的关键参数。

3.1基本几何参数贡献值分析

dw的样本点取值范围为［290，420］；tw的样本点取值范围为［30，42］；bf的样本点取值范围为［300，360］；tf的样本点取值范围为［30，44］。

由Isight软件进行计算可得肋骨基本几何参数对pt的贡献值线性分析结果，具体数据见图12，其中方格表示正效应，斜线表示负效应。由结果可知：dw对pt的贡献值最大且为负效应，为-41%；tw对pt的贡献值为28%；bf对pt的贡献值为21%；tf对pt的贡献值为10%。所以在肋骨截面设计时，为避免肋骨的侧向失稳，可以减小dw，tw，bf和tf。

图12　基本几何参数对pt的贡献值分析结果Fig.12 Contribution value of basic geometric parameters to elastic tripping pressure

3.2中间几何参数贡献值分析

Y0样本点取值范围［225，300］；Ips的样本点取值范围［5.3×108，9.4×108］；IZ的样本点取值范围为［1.2×107，1.5×108］；J的样本点取值范围［9.0×106，1.4×107］；Γ1的样本点取值范围［2.3×1012，1.6×1013］；Γ2的样本点取值范围［4.5×1010，8.5×1010］。

由Isight软件进行计算可得中间参数对pt的贡献值分析结果，具体数据见图13，其中方格表示正效应，斜线表示负效应。由结果可知：J对pt的影响最大且为正效应，对应的贡献值为36%；其次是Ips，对pt的贡献值为-28%；IZ，Γ1，Y0和Γ2对pt的贡献度分别为23%，10%，-2%和1%。

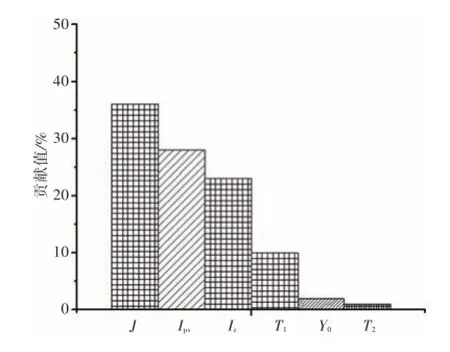
图13　中间几何参数对pt的贡献值分析结果Fig.13 Contribution value of intermediate geometric parameters to elastic tripping pressure

所以在肋骨形式的设计中，为提高肋骨侧向稳定性可以适当增加J和IZ，减小Ips。

基于肋骨的侧向失稳机理和解析解公式，得到了几何参数对肋骨侧向稳定性的影响规律：

4　结论

1）基本几何参数：肋骨侧向失稳临界压力随肋骨腹板高度的增大而减小，随腹板厚度、翼板宽度和翼板厚度的增大而增大。所以在肋骨尺寸设计中，为提高肋骨侧向稳定性，可以适当减小肋骨腹板高度，增大腹板厚度、翼板宽度和翼板厚度。

2）中间几何参数：肋骨侧向失稳临界压力随型心高度和剪切中心极惯性矩的增大而减小，随对称轴截面惯性矩、扭转惯性矩、纵向翘曲常数和横向翘曲常数的增大而增大。所以在肋骨尺寸设计中，为提高肋骨侧向稳定性，可以适当减小型心高度和剪切中心极惯性矩，增大肋骨的对称轴截面惯性矩、扭转惯性矩、纵向翘曲常数和横向翘曲常数。

3）各参数贡献值分析：在肋骨的基本几何参数中，肋骨腹板高度对肋骨侧向失稳临界压力的影响最大，产生负效应；其次是腹板厚度和翼板宽度，产生正效应，所以在肋骨的尺寸设计中，应着重考虑参数腹板高度、腹板厚度和翼板宽度对肋骨侧向稳定性的影响。在肋骨的中间几何参数中，扭转惯性矩对肋骨侧向失稳临界压力的影响最大，产生正效应；其次是剪切中心极惯性矩，产生负效应；再者是对称轴截面惯性矩，产生正效应；其余的中间几何参数影响相对较小。所以在肋骨的尺寸设计中，应着重考虑肋骨的扭转惯性矩、剪切中心极惯性矩和对称轴截面惯性矩对肋骨侧向稳定性的影响。

［1］MORANDI A C，FAULKNER D，DAS P K.Frame tripping in ring stiffened externally pressurised cylinders［J］.Marine Structures，1996，9（6）：585-608.

［2］郭日修.英国海军潜艇结构的设计思想和设计方法评述［J］.海军工程学院学报，1985（9）：86-97.

［3］包世华，周坚.薄壁杆件结构力学［M］.北京：中国建筑工业出版社，1991.

［4］刘勇，张政，徐治平.环肋圆柱壳肋骨侧向稳定性加强措施研究［J］.船舶工程，2008，30（3）：24-26. LIU Yong，ZHANG Zheng，XU Zhiping.Study on the improvement measurements for frame tripping in the ring stiffened cylinders［J］.Ship Engineering，2008，30 （3）：24-26.

［5］KENDRICK S.Design for external pressure using general criteria［J］.International Journal of Mechanical Sciences，1982，24（4）：209-218.

［6］KENNARD E H.Tripping of T-shaped stiffening rings on cylinders under external pressure［R］.W ashington DC:David TaylorModel Basin，1959.

［7］ADAMCHAK JC.Design equations for tripping of stiffeners under inplane and lateral loads［R］.Bethesda MD:David Taylor Naval Ship Research and Development Center，1979.

［8］FAULKNER D.The collapse strength and design of submarines［M］.England：University of Glasgow，1983.

［9］高灵芝.大型深潜潜艇耐压船体结构设计研究［D］.哈尔滨：哈尔滨工程大学，2003.

［责任编辑：田甜］

Effects of geometric parameters on frame tripping in the ring stiffened cylinder

WU Fan1，WANG Jin1，LIU Yong2，HUA Lin11 Department of Naval Architecture Engineering，Naval University of Engineering，Wuhan 430033，China 2Wuhan Second Ship Design and Research Institute，Wuhan 430205，China

Ring stiffened cylinders usually weld ring frames along the circumferential direction to improve the stability.In this case，the frame tripping is of great significance to the overall stability of ring stiffened cylinders.According to the mechanism and the analytical solution of frame tripping，the relationship between the geometric parameters of ring stiffened cylinders and their elastic tripping pressure are analyzed both theoretically and experimentally.The contribution of different geometric parameters of ring stiffened cylinders is studied，and the effects of geometric parameters on frame tripping is finally obtained.

ring stiffened cylinder；external pressure；buckling；frame tripping；geometric parameter；contribution value

U663.1

A

10.3969/j.issn.1673-3185.2015.04.009

2014-10-20网络出版时间：2015-7-29 9:33:59

吴梵，男，1962年生，博士，教授，博士生导师。研究方向：船舶结构力学。E-mail：wufang.135@163.com王金（通信作者），男，1990年生，硕士生。研究方向：船舶结构力学。E-mail：wang901002@126.com