新型人字齿同步带带轮齿廓曲面加工特性研究
郭建华,姜洪源,胡清明,孟庆鑫
(1.哈尔滨工业大学 机电工程学院,黑龙江哈尔滨150001;2.齐齐哈尔大学机电工程学院,黑龙江 齐齐哈尔161006)
啮合传动是机械传动中重要形式,不同的啮合方式中轮齿廓曲线形式不同,如渐开线齿廓[1]、圆弧齿廓、摆线齿廓、双渐开线齿廓[2]及其他齿轮,如非对称斜齿廓、正交面齿轮[3]、标准圆弧线圆柱齿轮、椭圆齿轮[4]、圆形螺旋锥齿轮[5]等,进行滚切加工过程中都涉及根切问题。研究根切的本质是找出根切原因,分析根切可能导致齿形变化是否能满足设计要求,以便设计、加工时力求避免根切发生。研究根切问题需从啮合原理研究入手,假设Σ2是形成齿轮齿面Σ1的工具面,数学上防止根切是包络齿廓曲面Σ1上出现奇异点[6]。
同步带轮的加工通常由专用滚刀加工,且由于同步带传动形式的特殊性,需对带轮全部轮廓进行加工。新型人字齿同步带传动设计具有寿命长、传动精度高、传动噪声低等传动特点[7-9]。采用范成原理加工的带轮齿廓能否实现设计要求,将直接影响传动设计效果。人字齿带轮由左右旋带轮装配而成,单只螺旋带轮齿廓是由7段空间曲面连接而成。本文根据新型人字齿同步带与带轮传动啮合关系建立带轮加工刀具齿面空间模型,研究刀具曲面Σ2与带轮曲面Σ1之间共轭条件、瞬时啮合线形成、包络齿廓曲面Σ1的根切界限函数、工具面Σ2上啮合界限函数计算公式。通过数值计算分析,研究各空间曲面的瞬时啮合线形成原理,分析根切界限和啮合界限条件,为刀具设计提供理论依据。
1 新型人字齿同步带带轮刀具齿廓曲面建模Σ2
刀具曲面Σ2模型由法面齿形做螺旋运动形成。齿条刀具曲面Σ2与加工带轮曲面Σ1坐标系转换关系,见图1。
人字齿同步带轮滚刀法面齿廓为对称齿形,齿廓方程建立在法面坐标系 σn=[on;xn,yn,zn]中,右侧齿廓由直线ab、顶弧(rp1)bc、侧弧(rp2)cd、根弧(rp3)de组成。各段曲线采用极坐标表示,且各圆弧连接点对应极坐标转角分别为 θb、θc、θd、θe。刀具法面齿廓分段矢量方程为:

式中:(rix,riy)i=1,2,3,表示圆弧曲线bc、cd、de圆心坐标。斜齿条固连在端面坐标系σ2=[o2;x2,y2,z2]中,原点o2为齿对称线与节线交点,齿条空间三维曲面Σ2表达式为:

式中:β为螺旋角,u为刀具沿z方向距离。将方程(1)代入(2)中,得到刀具齿条在σ2中平面、3段圆弧曲面Σ2参数方程:
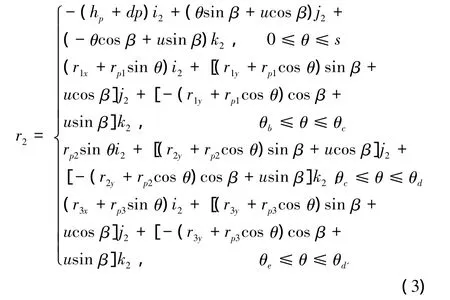
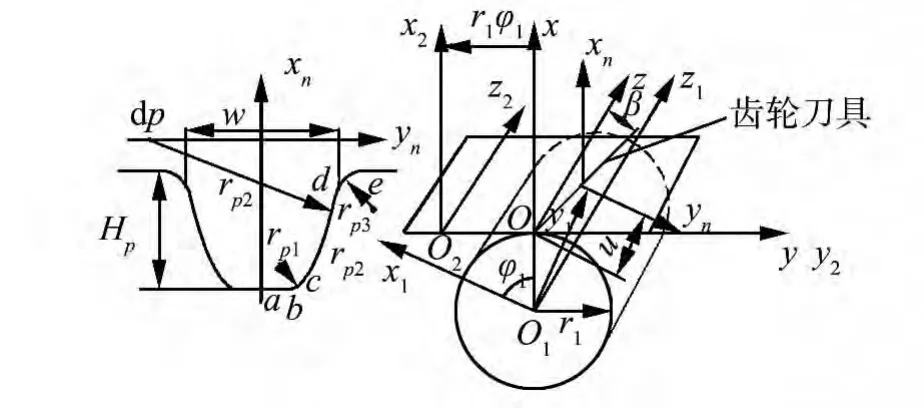
图1 齿条刀具与加工带轮坐标系转换关系Fig.1 Coordinate conversion relationship of hob and pulley
方程(3)中Σ2曲面矢径r2为关于u和θ的分片曲面函数,θ取值区间不同,对应曲面不同。
2 确定刀具曲面Σ2与带轮曲面Σ1啮合方程及带轮曲面Σ1方程
斜齿条刀具曲面Σ2加工带轮曲面Σ1,如同一对共轭啮合的空间齿条、齿轮传动。对于斜齿条刀具与带轮关系,采用瞬时回转轴法确定啮合函数。共轭接触面Σ2上的瞬时接触点的法线应当通过啮合轴z,见图1。在σ2中法线方程为:

式中:曲面 Σ2上nx2、ny2、nz2为法矢n2在坐标系 σ2中分量;X2、Y2、Z2分别为法线与啮合轴的交点X2=0、Y2=r1φ1、Z2=0坐标,r1和φ1分别代表带轮的节圆半径和转角。参数代入式(4)得:
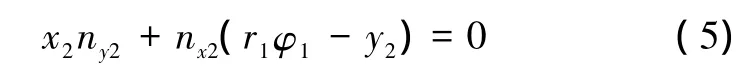
在曲面Σ2上法矢定义:

由式(6)得平面和圆弧段曲面的法矢方程为:

式中:θj中j代表b、c、e;θl中l代表c、d及d'。将式(7)代入式(5)分别得出直线段与3圆弧曲线段瞬时啮合线统一表达式为:

利用图1坐标系σ2到坐标系σ1的变换关系,联立式(3)和(8),得带轮曲面Σ1分片曲面方程,对应刀具平面的带轮曲面方程为:
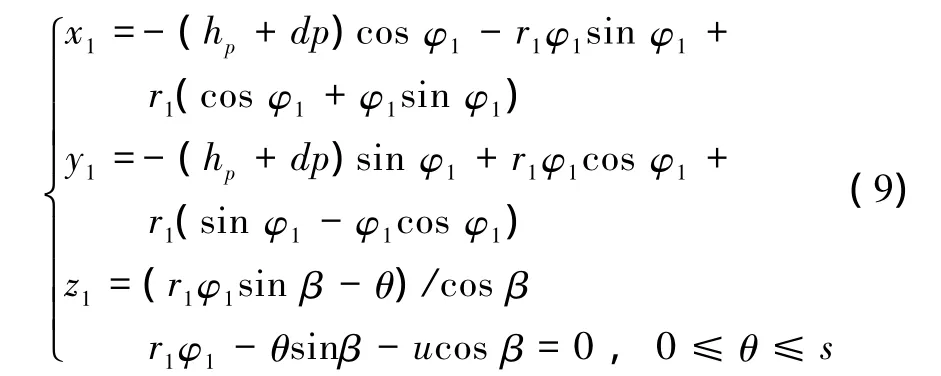
对应刀具圆弧曲线bc的带轮曲面方程为:

对应刀具圆弧曲线cd的带轮曲面方程为:

对应刀具圆弧曲线de的带轮曲面方程为:

3 确定带轮曲面Σ1根切界限点和刀具曲面Σ2啮合界限点
斜齿条刀具加工带轮时,带轮曲面Σ1不产生根切点方程为
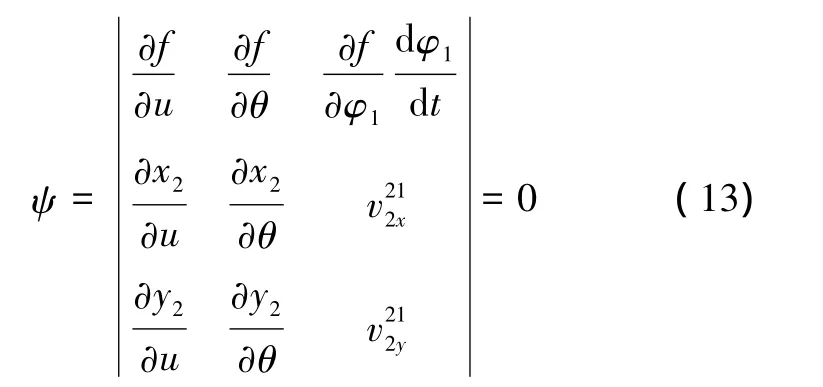
曲面Σ2与Σ1接触点的相对运动速度v(21)2是齿条以角速度ω(21)2=ω(1)·k2绕瞬时轴Z回转速度:
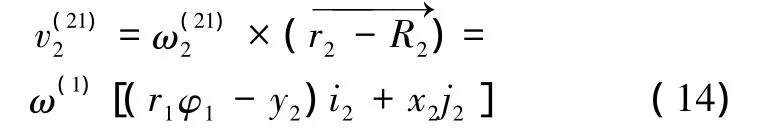
将(14)代入(13)得根切界限方程为:
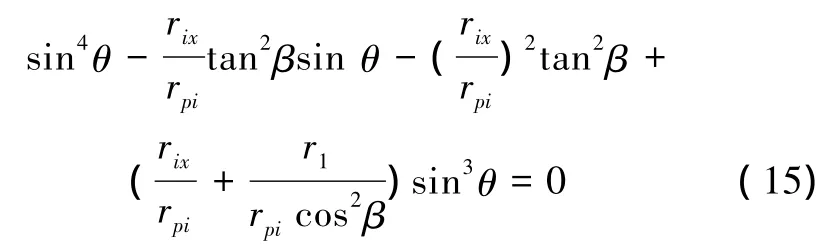
或

满足刀具齿面Σ2参与切削带轮曲面Σ1啮合界限点方程是对方程(8)求导得:
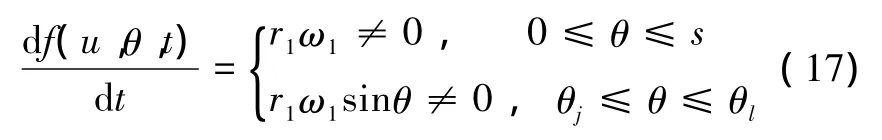
刀具曲面Σ2上没有啮合界限点曲线,曲面Σ2全部参加加工带轮曲面Σ1,刀具曲面Σ2建模是合理的。
4 带轮齿廓曲面加工特性分析
表1提供滚刀法面齿廓的标准齿形参数,图2表示加工齿数Z=34、带轮宽16 mm、螺旋角30°,当φ1=0.1 rad时,带轮齿廓曲面Σ1和其上形成的瞬时啮合线。式(8)刀具侧弧段cd,形成瞬时啮合线方程式:r1φ1-(0.5w-rp2)sinβ-ucosβ=0,与弧极坐标转角θ无关,转角φ1一定,瞬时接触线是距端面u距离法平面上半径为rp2的圆弧曲线,刀具的齿顶圆弧bc、齿根圆弧de、齿顶直线段ab形成的瞬时啮合线是空间曲线。瞬时接触线延长,在带轮加工过程中,加工末期切削阻力剧增,引起滚齿机振动,影响加工精度。根据上述理论分析制定特殊切削方案,带轮加工过程得到满意的结果。

表1 刀具法面齿形参数Table 1 Parameters of hob normal tooth profile

图2 带轮齿槽曲面与瞬时啮合线Fig.2 Profile of pulley groove and Instantaneous meshing line
图3表示不产生根切的最小带轮齿数与刀具各段圆弧转角范围关系。式(15)影响根切临界点参数r1或齿数z、θ。刀具齿顶圆弧rp1和侧弧rp2在给定的θ范围内,如图3(a)、(b)没有产生根切。刀具根圆弧rp3在90°≤θ≤169.6°范围内,如图3(c)产生根切。对应最小齿数22时,θ=157°。转角达到最大值 θ=167.6°,不根切齿数z=253。满足式(16)条件,意味θ=±90°,产生根切临界点。在刀具bc弧端点b,de弧端点e是根切临界点,因是曲线端点对带轮齿廓无影响。
通过仿真分析,刀具齿根弧rp3形成的变态渐开线等距曲线为折返线,折点为根切点J,如图4。随不根切临界齿数增大,根切点J与刀具侧弧与根弧交点的共轭点d逼近。当z<253,根切点J和交点d在带轮齿侧与带轮齿顶交点D右上侧,实际加工时,带轮的实际轮廓曲线为EDC,根切点J和交点d在切削时已经切掉,对齿廓无影响。

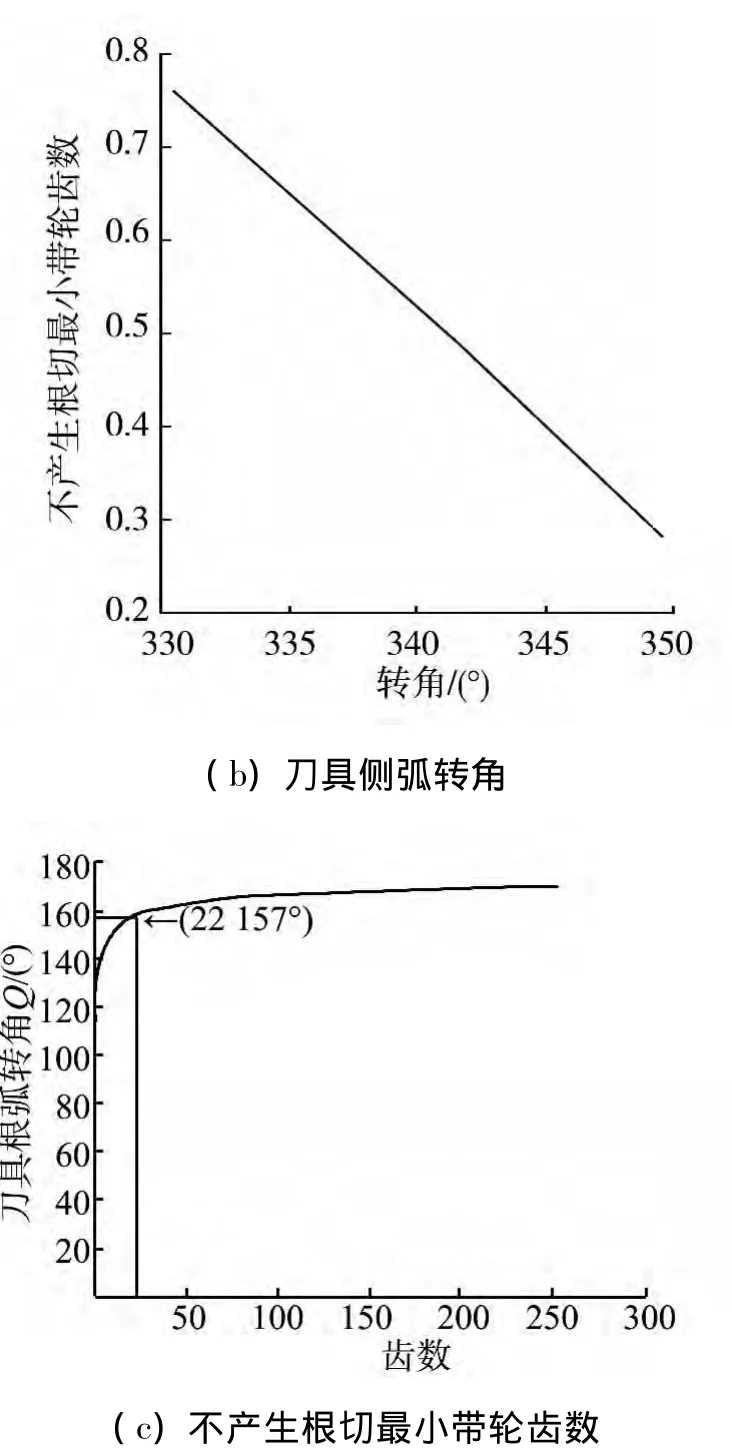
图3 不产生根切的最小带轮齿数与圆弧转角关系Fig.3 Relationship of minimum pulley teeth without undercutting and arc angle

图4 根切点与带轮齿槽关系Fig.4 Relationship of undercutting point and pulley groove
5 结论
基于新型人字齿同步带传动机理,建立加工带轮滚刀刀具曲面Σ2空间齿廓模型,并对加工过程带轮形成曲面Σ1特性进行计算研究,得出如下结论:
1)通过对刀具空间齿廓曲面Σ2函数与啮合函数计算,得出刀具齿廓曲面Σ2模型不存在啮合界限点,且模型建立合理。
2)刀具加工带轮齿廓曲面Σ1存在2种根切界限点,一是刀具曲面Σ2顶弧b点和根弧e点,但它们是曲线端点,不会产生根切;另一是带轮齿顶的变态渐开线等距曲线,存在根切,但实际切削过程中根切点位置被刀具齿侧弧形成曲面切掉。带轮齿面产生“棱线D”,齿数越小,越明显。消除棱线方法对刀具进行修形设计。
3)刀具齿侧弧加工带轮形成的共轭瞬时啮合线为该法面半径相等的圆弧,刀具齿廓其他曲线部分形成的瞬时啮合线越远离法平面空间曲线且延长曲折,瞬时接触线越长,切削阻力越大,易引起机床振动。基于上述理论研究,实际加工过程中通过控制滚刀参与切削的齿数,可降低切削阻力并保证带轮加工质量。
[1]ALIPIEV O,ANTONOV S,GROZEVA T.Generalized model of undercutting of involute spur gears generated by rack-cutters[J].Mechanism and Machine Theory,2013,64(6):39-52.
[2]樊智敏,朱东华.圆柱齿轮啮合干涉及根切的分析研究[J].机械设计与制造,2003,8(4):24-26.FAN Zhimin,ZHU Donghua.Analysis and study on meshing interference and undercutting of cylindrical gears[J].Mechinery Design and Manufacture,2003,8(4):24-26.
[3]李政民卿,朱如鹏.正交面吃轮齿廓的几何设计和根切研究[J].华南理工大学学报,2008,36(2):78-82.LIzheng Minqing,ZHU Rupeng.Investigation into geometrical design of tooth profile and undercut for orthogonal face gear[J].Journal of South China of Technology,2008,36(2):78-82.
[4]BAIR B W.Computer aided design of elliptical gears[J].Journal of Mechanical Design,2002,124(4):787-793.
[5]FONG Z H,TSAY C B.The undercutting of circular-cut spiral bevel gears[J].Mech.Des,1992,114(2):317-325.
[6]TEWEN L.Principles of gear connection [M].(s.l.):The Shanghai Science and Technology Publishing House,1984:288-296.
[7]MICHAEL J,GREGG W.Synchronous drive belt using helical offset teeth[C]//The Meeting of the Rubber Division,American Chemical Society.Chicago,Illinois,1999:55-68.
[8]郭建华,郑娜,姜洪源,等.基于ANSYS的新型人字齿同步带受力分析[J].机械传动,2012,36(2):60-62.GUO Jianhua,ZHENG Na,JIANG Hongyuan,et al.The finite element analysis of double helical synchronous belt based on ansys[J].Mechanical Transmission,2012,36(2):60-62.
[9]姜洪源,郭建华,胡清明,等.基于高阶接触啮合理论的新型人字齿同步带传动设计[J].机械传动,2013,37(8):17-20.JIANG Hongyuan,GUO Jianhua,HU Qingming,et al.Double helical synchronous belt transmission design based on theory of high degree contact mesh[J].Mechanical Transmission,2013,37(8):17-20.

