曝气条件对等温层曝气器充氧性能的影响

孙 昕,刘凌炜,段飞飞,解 岳 （西安建筑科技大学环境与市政工程学院,陕西 西安 710055）

曝气条件对等温层曝气器充氧性能的影响

孙 昕*,刘凌炜,段飞飞,解 岳 （西安建筑科技大学环境与市政工程学院,陕西 西安 710055）

分析了等温层曝气器曝气室内气泡—水接触界面的氧传质过程,确定了表征氧传质效果的各项参数,在双膜理论基础上建立了等温层曝气充氧动力学模型及其解析方法.应用本模型预测了美国 Prince湖等温层曝气器的充氧效果.根据等温层曝气充氧动力学模型的预测结果,随曝气量的增加和气泡直径的减小,氧总传质系数和氧传质速率均增大；随曝气量和气泡直径的增大,曝气效率下降.在等温层曝气器结构固定的情况下,减小气泡直径和增加水深均有利于改善曝气室的充氧效果,尤其是当气泡直径达到 μm级别时；当曝气量超过一定临界值0.06m3/s时,曝气室的充氧效果略有削弱.根据曝气量对氧传质速率、曝气效率和单位时间内曝气室的充氧量的影响特性曲线,可确定等温层曝气器的优化运行条件.

等温层曝气；溶解氧；模型；曝气量；气泡直径

目前,传统的水处理链已延伸扩展为包括源头和龙头在内的全流程处理链,针对微污染的水源水,采用对水源进行原位水质控制的综合成本远低于在水厂内进行预处理、强化常规处理和深度处理的综合成本,水源水质污染控制的重要性正逐渐被水处理界认识和重视［1-2］.

等温层曝气是指在不破坏水温分层的前提下,提高等温层水体溶解氧浓度,抑制湖库底泥中内源污染物的释放,同时给水体底部冷水生物提供良好的栖息场所［3-5］.等温层曝气虽然是解决分层湖泊水库内源污染的一项有效技术,各类等温层曝气设备也相继问世；但经过半个世纪的大量测试和研究,目前在富营养化湖库水质污染控制中的实际应用并不十分成功［6-8］.究其原因,等温层曝气是一种复杂的气-水两相流运动和传质过程,准确表征曝气室内氧传质过程和预测氧传质效果是该技术应用的瓶颈所在,等温层曝气器充氧性能的准确预测十余年来一直未有实质性进展,导致等温层曝气器充氧性能的理论预测与实际运行效果差异较大.等温层曝气器的运行能耗和成本不菲［9-10］,优化等温层曝气器的运行条件对节能减排也有重要的现实意义.

等温层曝气器曝气室内充氧效果取决于氧的传质效率和空气与水的接触时间,这些都和曝气量引起的表观水流速度以及气泡大小引起的气-水接触面积等直接相关.但由于过去表观水流速度的预测误差较大,一般与实测值差别± 20%～30%［11-12］,导致氧传质效率和空气与水的接触时间存在较大误差.在等温层曝气器外围的等温层水体,溶解氧浓度的改善效果还取决于循环水量和曝气室内的充氧效果.本文在预测曝气室表观水流速度的基础上,首先研究了等温层曝气器充氧动力学模型及其求解方法,然后运用该模型分析了曝气量和气泡直径对等温层曝气器充氧效果的影响,旨在为等温层曝气器的优化设计提供参考.

1　充氧动力学模型

1.1充氧动力学模型的构建

图1为等温层曝气器示意图.在曝气室内,水中主要发生2种氧传质过程：一是气泡在上升过程中发生的气泡—水界面氧传质,一是曝气室顶部累积的残余空气发生空气—水界面氧传质.由于曝气室顶部空气—水界面氧传质效率较低,本文仅考虑气泡—水界面这一主要的氧传质过程,由此在氧传质双膜理论［13］基础上建立等温层曝气充氧动力学模型.

根据双膜氧传质理论,曝气室内水体的充氧过程可表达如下：

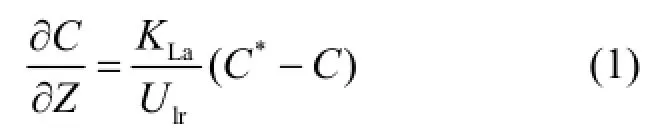
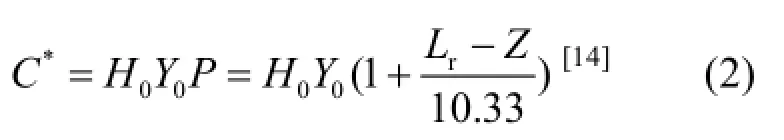
式中：C,C*分别为溶解氧与饱和溶解氧浓度（mg/L）,Z为纵坐标高度（m）, KLa为氧总传质系数（s-1）,Ulr为曝气室表观水流速度（m/s）, H0为亨利常数,Y0为氧组分百分比,P为气体压力（atm）,Lr为主空气扩散器距水面的高度（m）.

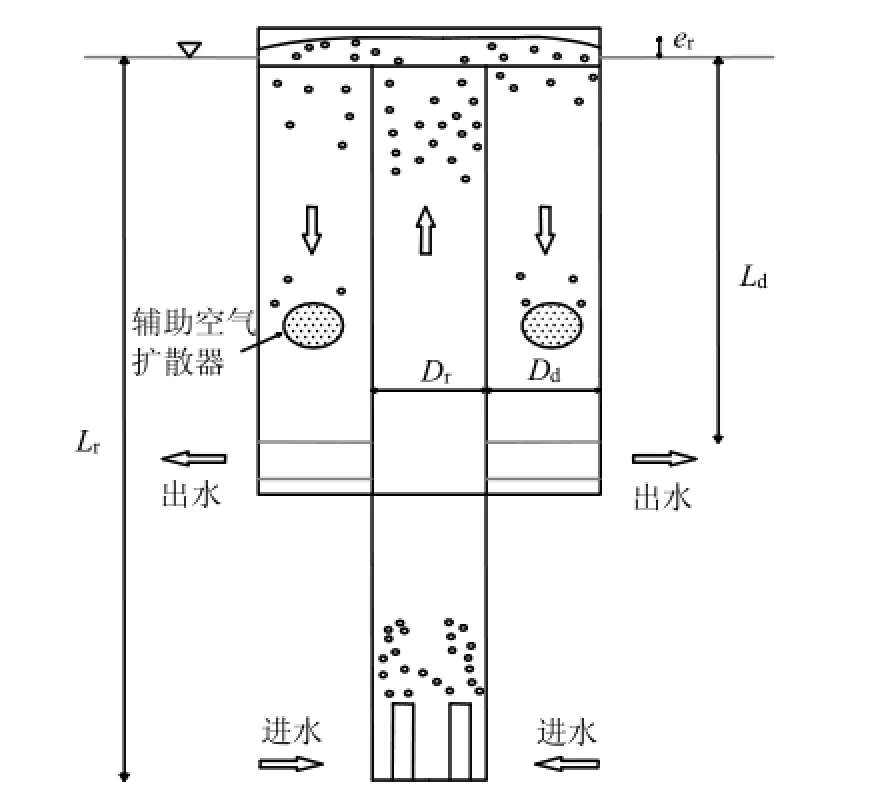
图1　等温层曝气器结构示意Fig.4　Schematic diagram of a hypolimnetic aerator

把方程（2）代入方程（1）积分得：

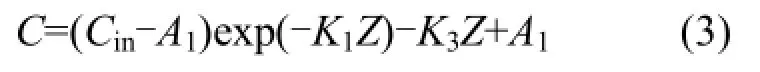
式中：Cin为曝气室入口处溶解氧浓度（mg/L）,

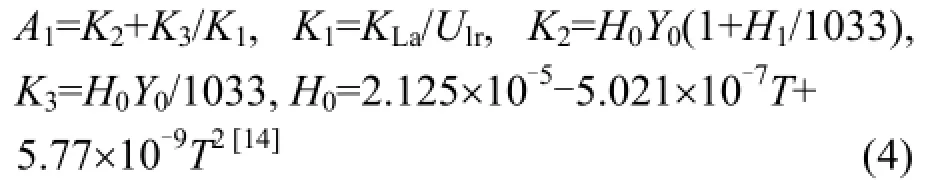
由方程（3）可见,距底部Z处的水中溶解氧浓度与该处水深、水温、表观水流速度和气泡性状（气含率、比表面积和氧传质系数等）有关,对方程（3）进行积分可求得不同水深处溶解氧浓度.由于不同水深处的溶解氧饱和浓度不同,为了计算准确,沿曝气室水流方向分段计算各段的 Kla,将前一段的出口溶解氧浓度 Cout作为后一段进口浓度Cin,分段的长度取为lm.

1.2动力学模型参数的确定

1.2.1氧传质系数 氧总传质系数（KLa）、氧水膜传质系数（KL）、气泡比表面积（a）可参见以下公式进行计算［11］：

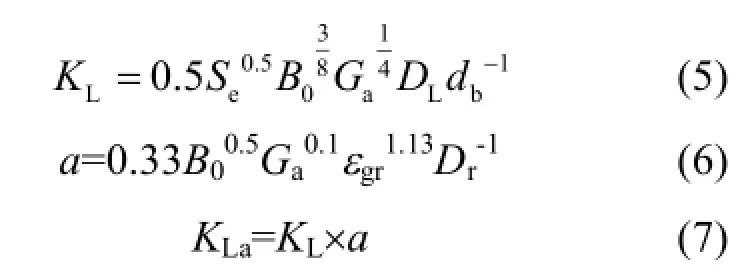
对于直径为mm以下的小气泡,其比表面积（a）可用下式表示［15］：

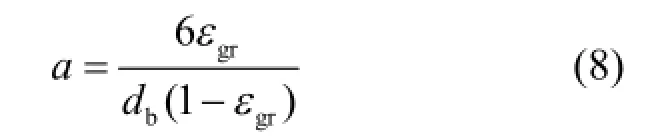
式中：Se、B0、Ga均为无量纲参数,,, db为气泡直径（m）,νl为液体运动系数（m²/s）,DL为氧的扩散系数（m² /s）,εg为气含率,Dr为曝气室上升筒直径（m）.

由于等温层曝气器曝气室内部流态不稳定,气泡在上升过程中各处尺寸及特性不一,这导致了单个气泡氧传质模型应用的复杂性与不确定性.在实际应用中,尽管已有一些学者提出了特征气泡直径（db,mm）的计算方法,如当量比表面直径（又称 Sauter-mean diameter）［12,15-16［17］；但由于曝气室内气-水两相流的复杂性和实验条件的限制,这些公式的应用均存在不少问题,本研究采用统一的平均直径（2.6mm）［12,16］.

1.2.2表观水流速度和气含率 等温层曝气器曝气室内气、液运动的驱动能量等效于曝气室内、外水体密度差产生的有效作用能量,曝气室内气、水两相流运动的总能量损失主要包括曝气室顶部、边壁、进出口及气泡尾涡产生的能量损失.根据驱动与损失能量的平衡关系,得到曝气室水动力学模型如下：

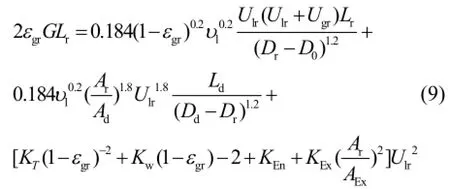
式中：G为重力加速度（m/s²）,Ugr为曝气室内表观气速（m/s）,Dr、Dd、D0分别为曝气室上升筒、下降管及曝气器中心管直径,m,Ld为下降筒高度（m）,Ar、Ad分别为上升筒、下降筒横截面积,m2, KT、KW、KEn、KEx分别为曝气室顶部、尾涡、曝气室上升筒入口、下降筒出口处局部能量损失系数,AEx为下降筒横截面积,m2.

曝气室内的气含率与表观水流速度之间关系可表示如下［14-15］：

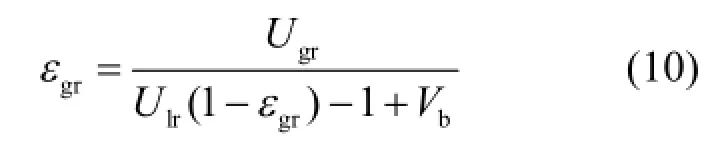
式中：Vb为气液相对滑移速度（m/s）,它与气泡半径（rb）关系为［14］：

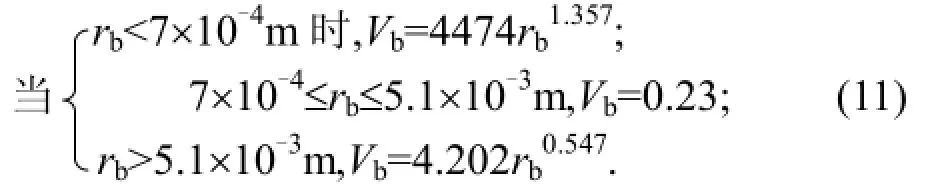
联立方程（9）～（11）,运用MATLAB的真域算法,可以求解曝气室内表观水流速度和气含率［18］.

1.3充氧性能表征及曝气条件

氧传质速率（OTR, g O2/s）是衡量等温层曝气器充氧性能的重要技术指标之一,它表示等温层曝气器曝气室水中单位时间内被转移的氧气量,其计算公式如下：

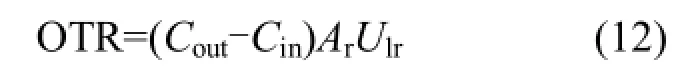
曝气效率（AE,g O2/kWh）是衡量等温层曝气器充氧性能的重要经济指标之一,它表示等温层曝气器单位电耗产生的充氧量（g O2/kWh）,其计算公式如下：

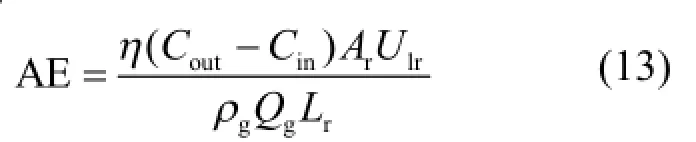
式中：ρg为空气密度,kg/m³,Qg为空气流量,m3.

以美国 Prince湖的等温层曝气器为实际案例,该湖平均水深10m,共安装有 10台等温层曝气器,每台等温层曝气器的结构和尺寸分别如图1和表1所示［11-12］.曝气量分别取为0.018,0.027, 0.035,0.046,0.056,0.063m3/h.

曝气器内主空气扩散器由两个直径3.8cm、高 0.86m的 PVC管构成,管壁均匀布设直径3.2mm微孔,辅助空气扩散器为直径25cm的橡胶微孔扩散器.空气流量、水流速度分别采用转子流量计和旋浆流速仪测定,测点分别位于供气管道和水深1.4m处.水温和溶解氧浓度采用610 型YSI水质分析仪测定.每组实验中,各参数数据测定10次,取其平均值.

表1　等温层曝气器结构尺寸（m）Table 1　structural sizes of a hypolimnetic aerator （m）

2　充氧动力学模型的验证

结合等温层曝气器的实际尺寸（表1）,运用方程组（9）～（11）,首先求得曝气室内表观水流速度和气含率,然后运用方程组（2）～（8）求出氧传质系数和溶解氧浓度.图2中预测值分别针对气泡直径 2.6,0.26，0.026mm,实测值仅针对气泡直径2.6mm.

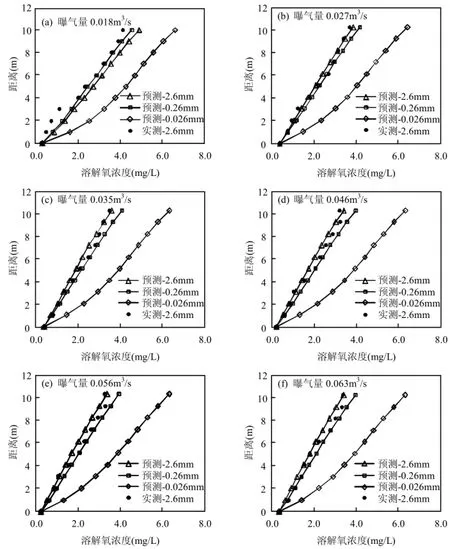
图2　曝气室距扩散孔不同高度处的溶解氧浓度Fig.4　Concentrations of dissolved oxygen at different heights above air diffusors in the aeration chamber

从图2可以看出：当气泡直径为2.6mm时,对于每一个曝气量而言,水中溶解氧的浓度均随距离扩散孔的高度的增加而增大,采用本文所建等温层曝气器充氧动力学模型预测的溶解氧浓度值与实测值吻合良好,说明在准确预测曝气室内表观水流速度和气含率的前提下,本文所建的充氧动力学模型具有较好的准确性和适用性,可以用于准确预测其他曝气条件（如曝气量和气泡直径）下曝气室内溶解氧浓度的垂向分布.

3　曝气条件对充氧效果的影响

3.1氧传质系数

当代的粉彩没骨花鸟画形式多样，构图新颖，设色绚丽，不再是千篇一律的程式化表达，更加注重个性与情感的表达。在多样化与个性化的特点之下，当代粉彩没骨花鸟画延续传统的随类设色的技法之外，还学习西方绘画的随环境设色的表现手法，运用焦点透视的科学处理技法，使得颜色表现形体之外，更有营造空间环境的功能。在构图上来说，当代粉彩没骨花鸟画传承古人的构图模式之外，也融入了现代的构图方式，同样也别具一格。

由图 3可见,气泡直径固定时,KLa值随曝气量的增加而增大,且气泡直径越小,增幅越明显.随曝气量从 0.018m3/s增加到 0.063m3/s,当气泡直径分别为2.6,0.26,0.026mm时,KLa值的变化范围分别为0.05～0.09s-1,0.10～0.15s-1和0.30～0.47s-1.主要有两方面的原因：一是曝气量增大时会在水膜表面产生较为剧烈的紊流,水膜的破坏和更新速度加快,导致氧的传质系数增大［19-20］；二是曝气量增大时会增加单位时间内水中的气泡数量,进而增大气-水界面的总面积［21］.

图3也说明,曝气量固定时,KLa值随气泡直径的减小而增大.主要有 4方面的综合原因［22-24］：一是增加单位体积内气泡的表面积；二是降低气-水相对滑移速度,相对延长空气与水的接触时间；三是减弱水膜表面的紊流,减小水膜传质系数；四是增加单位时间、单位水体内的气泡总数.在本研究条件下,气泡直径减小,气泡表面积的增加和气-水接触时间的相对延长对KLa值的增大贡献大于水膜传质系数的减小对KLa值的减小贡献.

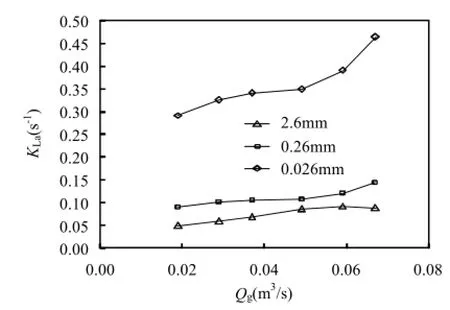
图3　曝气量和气泡直径对KLa的影响Fig.4　Effects of air flowrate and bubble diameter on KLa

3.2氧传质速率及曝气效率

由图4可见,气泡直径固定时,OTR值随曝气量的增加而增大,且气泡直径越小,增幅越明显.随曝气量从 0.018m3/s增加到 0.063m3/s,当气泡直径分别为2.6,0.26,0.026mm时,OTR值的变化范围分别为1.58～3.19,2.49～4.51,3.58～7.15g O2/s.局部而言,其原因与曝气量对 KLa值的影响原因相同,主要是由于水膜更新速度加快和水中气泡密度的增加.类似于 KLa,气泡直径的减小主要通过气泡表面积的增加和气-水接触时间的相对延长来增大OTR.

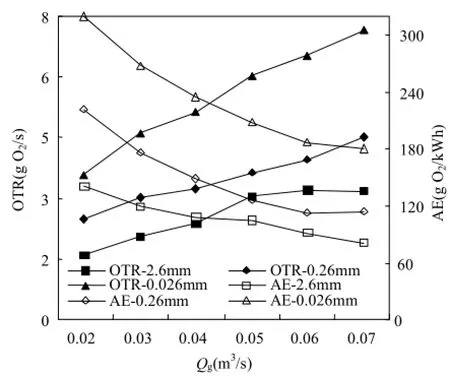
图4　曝气量和气泡直径对OTR和AE的影响Fig.4　Effects of air flowrate and bubble diameter on OTR and AE

由图3和图4可见,当气泡直径从2.6mm减小到0.26mm时,即气泡直径在接近mm级别范围变化时,等温层曝气器的充氧性能改善程度较小；而当气泡直径从2.6mm减小到0.026mm时,即气泡直径在接近μm级别范围内变化时,等温层曝气器的充氧性能改善程度非常明显.此结果也与其他水处理领域的相关研究结果类似［25-26］.

相对OTR而言, AE与曝气量成反比,与气泡直径成正比.由于深水曝气系统的能量效率一般较低（～10%）［10,27-28］,本案例水深较浅（～10m）,故取适当高值（η=20%）.计算结果表明（图4）,气泡直径固定时,AE值随曝气量的增加而减小,且气泡直径越小,减幅越明显.随曝气量从 0.018m3/s增加到0.063m3/s,当气泡直径分别为2.6,0.26, 0.026mm时,AE值的变化范围分别为 141～81, 222～114,320～181g O2/kWh.对于曝气系统,曝气效率一般随曝气量增加而降低,这与国内外其他研究结果一致［15,29］.主要有3方面原因,一是曝气量增加,曝气管路中气速增加,管路的能量损失增加,有效能量的比例减小；二是曝气室内的能量损失也增加,根据 Burris的报道［12］,当曝气量从0.018m3/s增加到 0.063m3/s时,曝气室内总能量损失从3043Pa增加到4459Pa；三是当曝气量增加到一定程度时,气泡直径会变大,气泡的比表面积会减小,气-水相对滑移速度减小,气-水相对接触时间缩短,共同导致氧传质减弱,如图中当曝气量增加到0.049m3/s以后,KLa值减小.

如果气泡直径极其微小（如＜0.002mm）,则空气扩散孔因其孔径低于该临界值,空气通过时还需克服表面张力而造成的巨大额外局部能量损失［15］,导致AE迅速下降；否则,曝气效率一般随气泡直径的减小而提高.本研究中气泡直径为0.026～2.6mm,远大于临界直径,故气泡直径对AE的影响特性与KLa及OTR类似.

3.3溶解氧浓度

如图5所示,气泡直径（db）对曝气室内溶解氧浓度的垂向分布产生重要影响.当等温层曝气器曝气量一定时,曝气室内相同水深处的溶解氧浓度随气泡直径的减小而增大.以曝气量0.018m3/s为例,当气泡直径从2.6mm减小10倍至0.26mm 时,曝气室顶部（距离扩散孔 10m）的溶解氧浓度从4.25mg/L增加到4.92mg/L,增加16%；而当气泡直径进一步较小100倍至0.026mm时,曝气室顶部的溶解氧浓度则迅速增加到6.78mg/L,增加59%.这说明减小气泡直径有利于提高等温层曝气器的曝气充氧效果,尤其是当气泡直径减小至微气泡级别时,主要原因是氧总传质系数的相应增大.

空气扩散孔之上的水深对曝气室内溶解氧浓度的垂向分布也产生较大影响.随着该水深（即距离空气扩散孔的高度）的增加,溶解氧浓度逐渐增加,这主要是由于气-水绝对接触时间的延长.以曝气量 0.018m3/s为例,在气泡直径为2.6mm的条件下,曝气室内溶解氧浓度从底部的0.32mg/L增加到顶部的4.25mg/L,增加近12倍.

相对气泡直径和水深而言,曝气量对曝气室内溶解氧浓度的影响较小,但随曝气量的增加,曝气室顶部溶解氧浓度呈现略有降低的趋势.当曝气室底部溶解氧浓度均为0.35mg/L时,同样可以预测不同曝气量和气泡直径条件下曝气室内的溶解氧浓度分布.以气泡直径2.6mm为例,当曝气量为 0.018m3/s时,曝气室顶部溶解氧浓度为4.26mg/L,当曝气量增加到 0.056m3/s时,曝气室顶部溶解氧浓度下降并基本维持在3.60mg/L,而当曝气量进一步增加到0.063m3/s时,曝气室顶部溶解氧浓度继续下降至3.34mg/L.其他气泡直径条件下的溶解氧结果与此类似.如果结合单位时间内曝气室内被传递的氧的总量,则曝气量在0.05m3/s时该值达到最大.

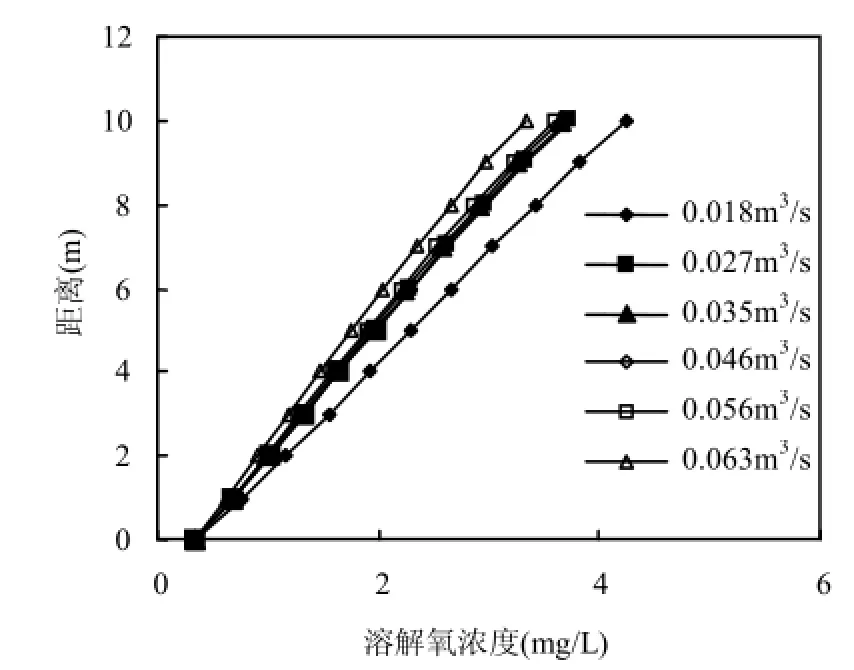
图5　曝气量对曝气室内溶解氧浓度分布的影响Fig.4　Effects of air flowrate on distributions of dissolved oxygen concentration in the aeration chamber

3.4充氧条件的优化

尽管局部范围内,曝气量的增加有助于氧传质,等温层曝气器的充氧能力会提高；但由于曝气会在曝气室内产生气-水两相流的上升运动,曝气量的增加会使曝气室内表观水流速度也增加,曝气室内气-水的绝对接触时间相应缩短,当曝气量增加到一定值后,曝气的整体充氧效果可能会下降,故在实际工程应用中应控制等温层曝气器的运行条件,以使其处于最优充氧状态.

从图4可以看出,随着曝气量的增加,等温层曝气器的曝气效率逐渐下降,即等温层曝气器的单位运行能耗逐渐增加,而等温层曝气器的充氧能力（即氧传质速率）一直随曝气量的增加而提高,二者随曝气量的曲线的交点可视为等温层曝气器的最优曝气量,由此可确定既定结构的等温层曝气器的优化运行条件.以气泡直径2.6mm为例,由图4得出的最佳曝气量约为0.04m3/s左右,而由图5得出的最佳曝气量也大体一致.

4　结论

4.1主要考虑等温层曝气器曝气室内气—水界面氧传质过程,基于水和气泡之间的双膜氧传质模型,建立等温层曝气氧传质模型,预测了不同工况条件下曝气室内溶解氧浓度的垂向分布,模型预测结果与实测数据吻合良好.

4.2根据模型预测结果,当等温层曝气器结构尺寸一定时,随着曝气量的增加和气泡直径的减小,氧总传质系数和氧传质速率均增大,等温层曝气器的充氧能力提高；随着曝气量和气泡直径的增大,等温层曝气器的曝气效率下降,其单位运行能耗增加.

4.3曝气室顶部溶解氧浓度随气泡直径的减小和空气扩散孔之上水深的增加而增大,而当曝气量增加到一定程度后,该浓度反而略有减小；根据氧传质速率和曝气效率与曝气量的关系曲线,结合单位时间内曝气室内被传递的氧的总量,可确定等温层曝气器的优化运行条件.

［1］ Tofflon M, Ragazzi M, Righetti M, et al. Effects of artificial hypolimnetic oxygenation in a shallow lake. Part 1：Phenomenological description and management ［J］.Journal of Environmental Management, 2013,114：520-529.

［2］ Gołdyn R, Podsiadłowski S, Dondajewska R, et al.The sustainable restoration of lakes—towards the challenges of the Water Framework Directive ［J］. Ecohydrology & Hydrobiology, 2014,14（1）：68-74.

［3］ 邵益生.关于我国城市水安全问题的战略思考 ［J］. 给水排水, 2014,40（9）：1-3.

［4］ Tao T, Xin K L. A sustainable plan for China's drinking water ［J］. Nature, 2014,511：527-528.

［5］ Beutel M W, Horne A J. A review of the effects of hypolimnetic oxygenation on lake and reservoir water quality［J］. Lake and Reservoir Manage, 1999,15：285-297.

［6］ Gantzer P A, Bryant L D, Little J C. Effect of hypolimnetic oxygenation on oxygen depletion rates in two water-supply reservoirs. ［J］. Water Research, 2009,43（6）：1700-1710.

［7］ Bryant L D, Hsu-Kim H, Gantzer P A, et al. Solving the problem at the source： Controlling Mn release at the sediment-water interface via hypolimnetic oxygenation ［J］. Water Research, 2011, 45（19）：6381-6392.

［8］ Cooke G D, Welch E B, Peterson S, et al. Restoration and management of lakes and reservoirs ［M］. Third edition. Taylor and Francis/CRC Restoration and Management of Lakes and Reservoirs, 2005.

［9］ Kirke B, Gezawy A E L. Design and model tests for an efficient mechanical circulator/aerator for lakes and reservoirs ［J］. Water Research, 1997,31（6）：1283-1290.

［10］ 孙 昕,叶丽丽,黄廷林,等.破坏水库水温分层系统的能量效率估算：以金盆水库为例 ［J］. 中国环境科学, 2014,34（11）：2781-2787.

［11］ Little J C, 1995. Hypolimnetic Aerators： Predicting Oxygen Transfer and Hydrodynamics ［J］. Water Research, 29（11）：2475-2482.

［12］ Burris V L, Daniel F M D, John C L, 2002. Predicting oxygen transfer and water velocity in airlift aerators［J］. Water Research, 36（18）：4605-4615.

［13］ 许保玖.给水处理理论 ［M］. 北京：中国建筑工业出版社, 2000.

［14］ Wüest A, Brooks N H, Imboden D M. Bubble plume modeling for lake restoration ［J］. Water Resources Research, 1992,28（12）：3235-3250.

［15］ Chisti MY. Airlift bioreactors［M］. New York, NY： Elsevier, 1989.

［16］ Mcginnis D F. Predicting diffused-bubble oxygen transfer rate using the discrete-bubble model. ［J］. Water Research, 2002, 36（18）：4627-4635.

［17］ Bakker W A M,van Can H J L,Tramper J, et al. Hydrodynamics and mixing in a multiple airlfit loop reactors.Biotechnology and Bioengineernig, 1993,42：994-1001.

［18］ Sun X, Duan F F, Huang T L, et al. Development and Sensitivity Analysis of Model for Aeration Chamber in Water-circulating Aerator ［J］. Applied Mechanics and Materials, 2013,260-261：663-668.

［19］ Li E, Zeng X Y, Fan Y H. Air-water ratio as a characteristic criterion for fine bubble diffused aeration systems ［J］. Chemical Engineering Journal, 2008,137（222）：214-224.

［20］ Miyahara T, Kawate O. Hydrodynamics of a solid-suspended bubble column with a draught tube containing low-densityparticles. Chem. Engng Sci., 1993,48,127-133.

［21］ Nagaosa R S. A numerical modelling of gas exchange mechanisms between air and turbulent water with an aquarium chemical reaction ［J］. Journal of Computational Physics, 2014, 256：69-87.

［22］ Livingston A G, Zhang S F. Hydrodynamic behaviour of threephase （gas-liquid-solid） airlift reactors ［J］. Chemical Engineering Science, 1993,48（93）：1641-1654.

［23］ Wongsuchoto P, Charinpanitkul T, Pavasant P. Bubble size distribution and gas-liquid mass transfer in airlift contactors ［J］. Chemical Engineering Journal, 2003,92：81-90.

［24］ 肖柏青,张法星,戎贵文.气泡尺寸对曝气池内气液两相流数值模拟的影响 ［J］. 中国环境科学, 2012,32（11）：2006-2010.

［25］ 魏春海,汪诚文,黄 霞.曝气孔开孔直径对一体式膜-生物反应器的影响 ［J］. 中国环境科学, 2007,27（2）：169-173.

［26］ 刘 春,肖太民,张 晶,等.微气泡曝气对生物膜反应器启动运行性能影响 ［J］. 中国环境科学, 2014,34（12）：3093-3098.

［27］ Zic K, Ellis H G S C. Laboratory study of water destratification by a bubble plume ［J］. Journal of Hydraulic Research, 1992, 30（1）：7-27.

［28］ Baines W D, Leitch A M. Destruction of stratification by bubble plume ［J］. American Society of Civil Engineers, 2014,118（4）：559-577.

［29］ Mavinic D S, Bewtra J K. Efficiency of diffused aeration systems in wastewater treatment ［J］. J. Water Pollut. Control Fed., 1976, 48：2273-2283.

Effects of aeration conditions on the oxygenation performance of a hypolimnetic aerator.

SUN Xin*, LIU Ling-wei, DUAN Fei-fei, XIE Yue （School of Environmental and Municipal Engineering, Xi'an University of Architecture and Technology, Xi'an 710055, China）.

China Environmental Science, 2015,35（9）：2690～2697

Oxygen transfer process from the air bubbles to the water was mainly analyzed in the aeration chamber of a hypolimnetic aerator, parameters characterizing the effectiveness of oxygen transfer were properly determined,a dynamical model of oxygen transfer for hypolimnetic aeration was developed based on the double-layer theory. The effectiveness of oxygenation was well predicted using the developed dynamical model of oxygen transfer for hypolimnetic aeration. Based on the predicted results using the dynamical model of oxygen transfer, when the air flowrate increased or the bubble diameter decreased, the oxygen transfer coefficient and the oxygen transfer rate increased. When the air flowrate and bubble diameter increased, the aeration efficiency decreased. Under fixed configuration conditions of a hypolimnetic aerator, decreasing the bubble diameter and increasing the water depth above the air diffusors would be helpful to improve the effectiveness of oxygenation in the aeration chamber of a hypolimnetic aerator, especially when the bubble diameter was of micrometer level. When the air flowrate increased to a critical value of 0.06m3/s, the effectiveness of oxygenation in the aeration chamber would become weaker. Judged from the influencing characteristic curves of air flowrate on the oxygen transfer rate, aeration efficiency and oxygen input of the aeration chamber per unit time, the optimized operational conditions of a hypolimnetic aerator can be determined.

hypolimnetic aeration；dissolved oxygen；model；air flowrate；bubble diameter

X524

A

1000-6923（2015）09-2690-08

2015-01-05

国家自然科学基金面上项目（51178379）；教育部高等学校博士点专项科研基金（20106120120012）；陕西省科技统筹创新工程计划项 目 （2015KTCL-03-15）；国家 科技 支撑 计划 课题（2012BAC04B02）；人力资源和社会保障部留学人员科研择优资助项目（DB03153）

*责任作者, 教授, xinsunn@gmail.com

孙 昕（1971-）,男,安徽桐城人,教授,博士,主要从事水质污染控制与模拟研究.发表论文30余篇.