基于权衡因子的决策树优化算法
董跃华, 刘力
(江西理工大学信息工程学院,江西 赣州341000)
基于权衡因子的决策树优化算法
董跃华,刘力
(江西理工大学信息工程学院,江西 赣州341000)
通过分析ID3算法的多值偏向问题和传统ID3改进算法中出现的主观性等问题,提出了一种基于权衡因子的决策树优化算法.该优化算法通过引入能够反映属性之间相互依赖关系的权衡因子,对取值个数最多的属性的划分权重重新进行权衡,以完成对ID3算法的改进.实例验证和标准数据集UCI上的实验结果表明,当数据集中属性的取值个数不相同时,优化后的ID3算法能够解决多值偏向问题,在构建决策树的过程中,优化后的ID3算法既能提高平均分类准确率,又能减少平均叶子节点数.
ID3算法;多值偏向;权衡因子;决策树;权重
0 引言
数据分类是数据挖掘中重要的组成部分之一[1],其中包含有决策树分类器、贝叶斯分类器、遗传算法、粗糙集和模糊逻辑等基本技术[2].决策树算法由于其分类精度高、生成的模式简单、算法易理解等特点而得到广泛应用.众多决策树算法中,ID3算法的影响力最大[3].
由于ID3算法采用信息熵的计算方式来选择分裂属性,易导致其产生多值偏向问题[4].针对ID3算法的多值偏向问题,很多学者进行了相关的改进工作:文献[5-8]引入用户兴趣度参数,用户兴趣度参数在一定程度上虽能克服多值偏向问题,但该参数的选取主要依靠用户丰富的先验知识和领域知识;文献[9-10]在文献[6]的基础上进行改进,引入灰色关联度代替用户兴趣度参数,虽在克服多值偏向问题上取得一定成效,但由于实际操作中易出现灰度较低或属性取值个数较多等情况而导致难以界定其范围.
本文引入统计学中的 λ相关系数[11],其公式完全由加、减、除基本运算组成,因此λ相关系数不仅可获得属性之间的相互依赖关系,且计算量较小.本文结合λ相关系数,在文献[6]的基础上提出基于权衡因子的决策树优化算法.优化的ID3算法在选取分裂属性时,因其以信息熵理论为基础从而继承原ID3算法较高的分类精度.用权衡因子替代用户兴趣度,既能克服多值偏向问题,又能避免选取的主观参数对决策结果造成影响.实验结果表明,在数据集存在多值偏向的趋势时,基于权衡因子的决策树优化算法,既能够克服多值偏向问题,又能提高分类精度,减少叶子节点数.
1 基本理论
1.1ID3算法
设训练集S有s个样本,将训练集分成m个类,第i类的实例个数为si.选择属性Ap划分训练集S,设属性Ap有属性值{S1,S2,…,Sj,…,Sk},Sj中属于第i类的训练实例个数为sij,则得到划分属性Ap的信息增益为[2]:
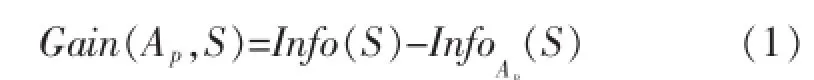
其中:
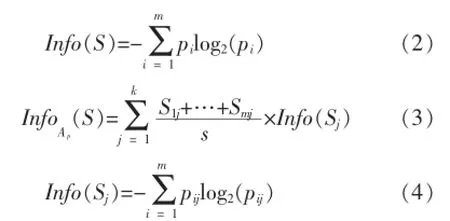
其中,pi是 S中属于第 i类的概率,pi=si/s;pij为 sj中第i类样本的概率,pij=sij/sj;
1.2基于用户兴趣度参数的ID3改进算法
信息熵的计算方式使得ID3算法的分裂属性的选择容易偏向于取值较多的属性,但拥有较多属性值的属性不一定是当前最佳分裂属性,因而就造成了ID3算法的多值偏向问题.文献[6]为克服多值偏向问题,在信息熵公式中引入用户兴趣度α(0≤α≤1),将子元组的划分权重加上α,则子元组对应需要的期望信息量公式(3)修改为[6]:
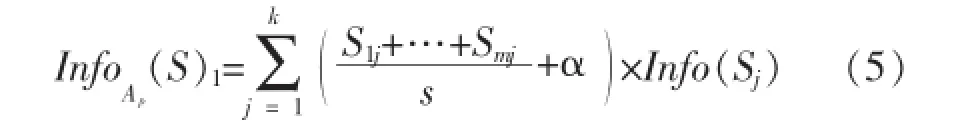
对应的信息增益公式(1)也将改进为:
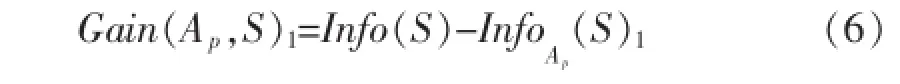
基于用户兴趣度参数的ID3改进算法是以公式(6)作为分裂属性的选择标准,同时该算法也存在一些不足之处:
1)由于用户兴趣度参数α的值需要由用户根据先验知识或者领域知识来确定,因此基于用户兴趣度参数的ID3改进算法带有很强的专业领域性,易给用户造成跨领域知识的学习负担[12].
2)当大部分属性数据规模较大且个别属性数据规模较小时,人们若因对属性的认识不够深刻而令给出的用户兴趣度不能正确反应属性自身的重要性时,则会导致出现大数据掩盖小数据的情况[13].
3)用户兴趣度由于是主观给出的划分权重参数,因此在一定程度上人为因素会影响最终的决策结果.
4)属性的用户兴趣度参数只有在经过大量实验和反复验证之后才能被正确的给出.
1.3λ相关系数
统计学中通常使用相关系数作为衡量变量之间密切相关程度的评价标准.由于被考量的变量存在不同的特性,因此变量对应表示的相关系数也存在多个种类,例如可用λ系数测定两个定类数据之间的密切相关程度,可用γ系数和皮斯尔曼等级相关系数测量两个定序数据之间的密切相关程度,可用ρ相关系数测量两个普通变量之间的密切相关程度[11].
其中,ρ相关系数的应用面较为广泛且限制条件较少,但其计算量较大.本文主要研究λ相关系数,相比较于ρ相关系数,λ相关系数也能评价变量之间的相关性且其计算量较小.λxy相关系数主要适用的情况为:在两个定类变量中,另外又分为自变量和因变量.其中,x代表自变量,共有n个值;y代表因变量,共有m个值,则λxy相关系数对应的计算公式为[14]:
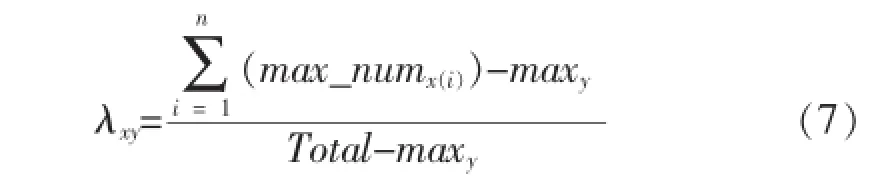
当自变量x取第i个值时,它与因变量y中m个值对应m个样本频数,在m个频数中取最大值即为max_numx(i);maxy为变量y的m个值中样本频数的最大值;Total为样本总数目.
λxy相关系数的绝对值越大,则表示变量x和y之间线性关系紧密相关程度越大;λxy相关系数的绝对值越小,则表示变量x和y之间线性关系紧密相关程度越小;λxy相关系数的绝对值为0时,称x和y不相关.
2 基于权衡因子的决策树优化算法
本文首先将λ相关系数引入到ID3决策树算法的研究领域中,提出基于ID3决策树算法的λ相关系数——DT_λ相关系数;然后再结合DT_λ相关系数得到属性的权衡因子;最后通过引入权衡因子对ID3算法进行改进,提出了基于权衡因子的决策树优化算 (Optimized algorithm of decision tree based on weighting factor)简称DTWF算法.
2.1DT_λ相关系数的引入
借鉴统计学中λ相关系数的定义,将变量间的λ相关系数引入到ID3算法中,使其成为定义条件属性与决策属性之间紧密相关程度的性能指标,从而得到基于ID3决策树的λ相关系数——DT_λ相关系数.
设有知识表达系统I=(U,R,V,f),其中R=C∪D且C∪D=Ø,设C为条件属性集C={A1,A2,…,Ap,…,An},D为决策类集合:D={D1,D2,…Di,…,Dm}.其中,属性Ap有属性值{S1,S2,…,Sj,…,Sk},k为Ap的属性取值个数,Sj中属于第i类的训练实例个数为sij,由此得到Ap的DT_λ矩阵.矩阵中第n+1行第j列表示决策属性Di的总样本个数,第i行第m+1列表示属性Ap的总样本个数.
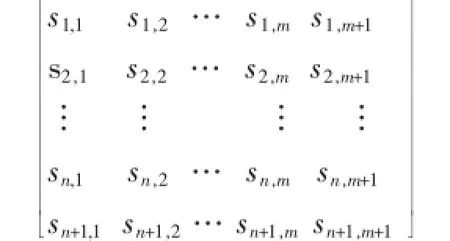
则属性Ap与决策类D的相关系数DT_λ(Ap)定义为:
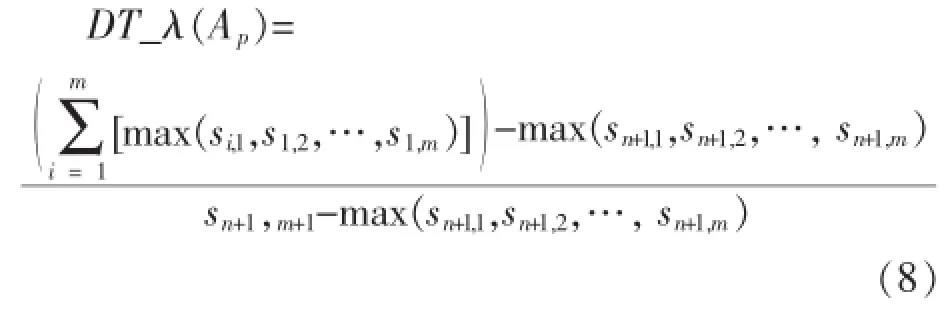
其中,max(si,1,si,2,…,si,m)表示条件属性 Ap对应决策属性集合D中最多的样本数,max(sn+1,1,sn+1,2,…,sn+1,m)表示训练集中,最多数的样本属于某一类的样本数,因此DT_λ(Ap)中的分子不大于分母,即DT_λ(Ap)∈[0,1).DT_λ(Ap)的值是ID3决策树中衡量条件属性与决策类之间相关性大小的指标,DT_λ(Ap)的值越大,则条件属性与决策类之间的相关程度越大.当DT_λ(Ap)=0时,则条件属性与决策类之间完全不相关.
2.2DTWF算法的提出
ID3算法的主要缺陷在于其多值偏向问题,为克服该问题,Quinlan在提ID3算法后,又提出C4.5算法.C4.5算法虽在一定程度上能克服多值偏向问题,但又会出现C4.5算法少值偏向问题.良好的ID3改进方法是既不偏向多值,又不少偏向少值,而DTWF算法的改进工作正是以此为目标.
本文提出DTWF算法的改进过程为:首先,根据信息增益公式(1)计算出每个条件属性的信息增益值,然后再从条件属性集C中挑选出信息增益值最大的属性Ap和属性取值个数最多的属性Aq;最后比较属性Ap和属性Aq.若属性Ap和属性Aq为同一属性,则表明在选择分裂属性的标准已偏向属性取值个数最多的属性,即已经产生了多值偏向问题,此时需要采用权衡因子对属性Aq的划分权重进行重新权衡,以克服多值偏向问题;若属性Aq和属性Aq不为同一属性,表明选择属性Ap作为分裂属性不会出现多值偏向问题.因此可将属性Ap的权衡因子WF(Ap)定义为:
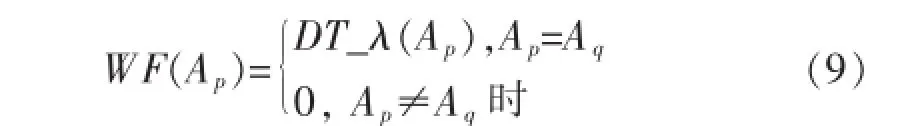
通过引入权衡因子WF(Ap)对ID3算法公式(1)进行改进从而得到DTWF算法,DTWF算法对应的信息增益公式为:
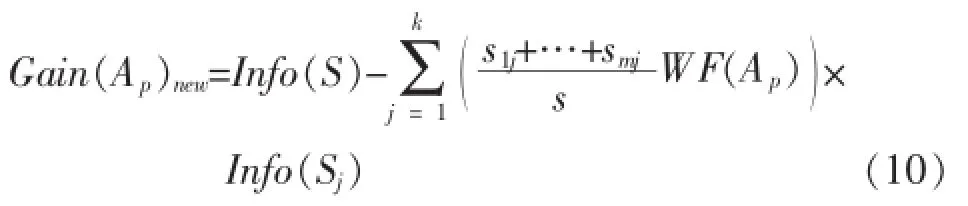
2.3DTWF算法伪代码
算法:DTWF(D,attribute_list)
输入:训练元组为D,属性均已完成离散化操作,候选属性集合为attribute_list.
输出:一棵DTWF决策树.
DTWF算法伪代码为:
DTWF(D,attribute_list)
{
创建节点N;
if D中所有子元组均属于同一个类C then
return N作为叶节点,并将N标记为类C;
if attribut_list为空then
return N作为叶节点,标记为D中的多数类;//由该节点中样本个数最多的类表示该节点的类别性质.
根据式(4)计算attribute_list中每个属性的信息增益,并选择出信息增益值最大的属性Ap和取值个数最多的属性Aq;
if Ap==Aq//此时属性Ap具有多值偏向的趋势,需要用权衡因子WF(Ap)重新权衡该属性的属性划分权重
then
{
根据式(8)计算属性Ap与决策类D之间的相关系数DT_λ(Ap);
令Ap的权衡因子WF(Ap)=DT_λ(Ap);
根据式(10)重新计算属性Ap的信息增益;
}
Else//此时属性Ap无多值偏向的趋势,该属性的属性划分权重不需要被权衡因子进行权衡操作
令属性Ap的权衡因子WF(Ap)=0;
将使用公式(10)计算后的属性Ap的新信息增益与其它候选属性的信息增益进行重新比较,并从中选取信息增益值最大的属性作为分裂属性splitting_attribute;
标记节点N为splitting_attribute;
for each splitting_attribute中属性值 Sj//根据splitting_attribute的属性取值Sj划分训练元组D
{
由节点N分出splitting_attribute中一个属性值为Sj的分枝,设Di是D中splitting_attr-ibute=Sj的数据元组集合;//进行一次划分
if Di为空then
由节点N分出分一个树叶,标记为D中的多数类;//由该节点中样本个数最多的类代表该节点的类别性质
else{
由节点N分出分一个由 DTWF(Di,attribute_list减去splitting_attribute)返回的节点;
}
}
}
3 实验及结果分析
3.1实验说明及评价标准
选取UCI上的6组标准数据集(如表1)进行实验数据分析,其中前3组数据集的属性取值个数相同,后3组数据集的属性取值个数不相同.数据集中2/3样本作为训练集,1/3作为测试集.采用文献[15]方法对数据集中的连续性属性进行离散化操作.
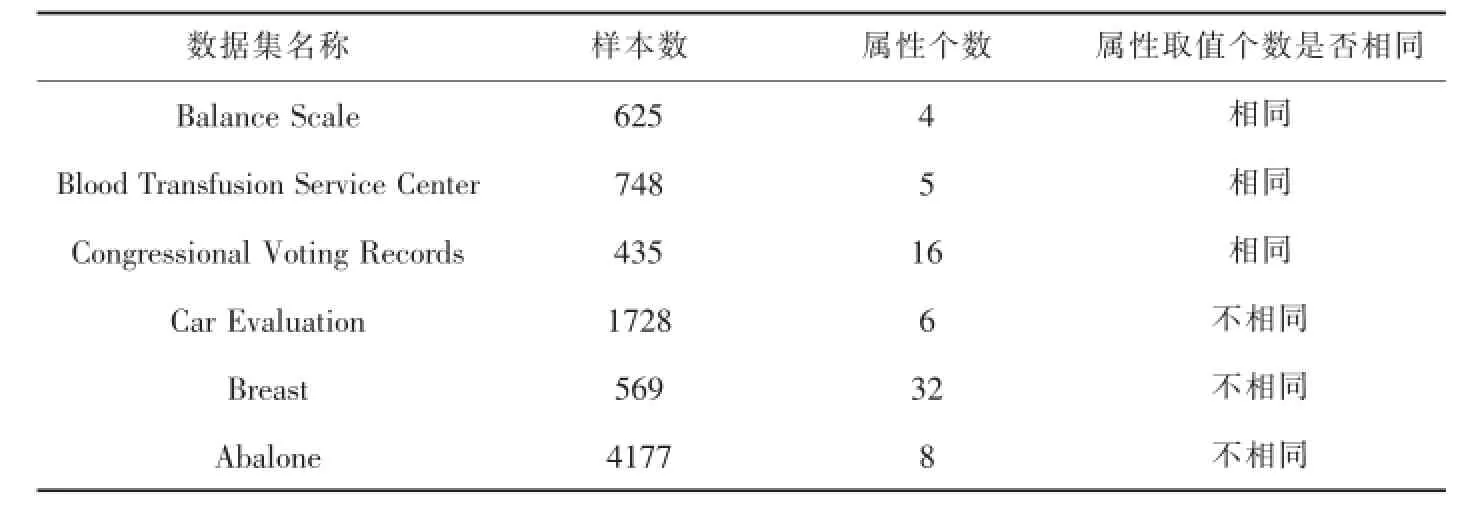
表1 数据集
采用商务购车顾客数据库(如表2)作为训练集D,对数据进行选取、预处理和转换操作后得到样本集合,该集合包含4个条件属性:喜欢的季节(含4个属性值:春天、夏天、秋天、冬天)、是否商务人士(含2个属性值:是、否)、收入(含3个属性值:高、中、低)、驾车水平(含2个属性值:良好、一般).样本集合根据类别属性“是否买车”(含有2个属性值:买、不买)进行划分.
本实验采用WEKA平台,实验使用的计算机配置:CPU为酷睿i5 2300系列,主频为2.8 GHz,内存为4 GB,操作系统为win 7,仿真软件为Matlab R2012a.
分类准确率是分类问题中常用的评价标准,能体现出分类器对数据集的分类性能[16].分类准确率指分类器中被正确分类的样本个数在总的检验集中所占比例,其公式为[2]:
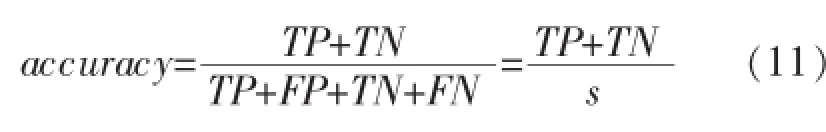
其中,s为总的样本个数;TP表示分类器预测为正时,真实类别为正的样本个数;FP表示分类器预测为正时,真实类别为负的样本个数;TN表示分类器预测为负时,真实类别为负的样本个数;FN表示分类器预测为负时,真实类别为负的样本个数.
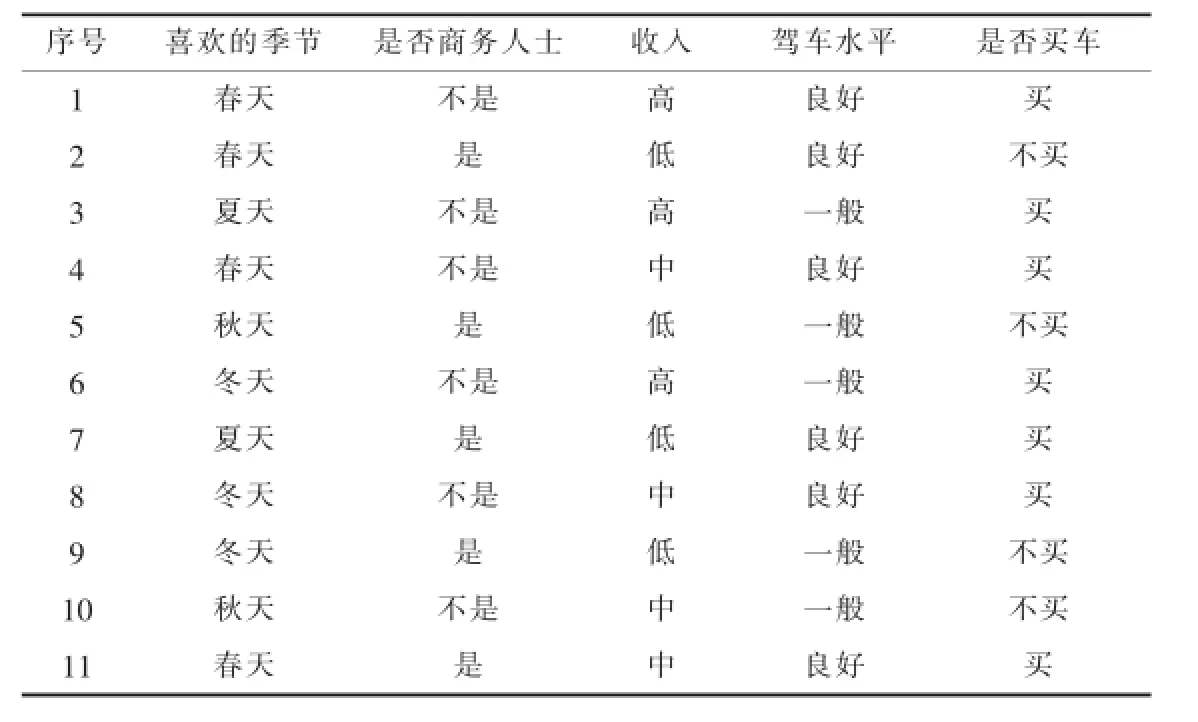
表2 顾客数据库训练集D
3.2DTWF算法的实例验证与分析
以训练集D为例,根据公式(1)计算ID3算法信息增益,根据公式(10)计算DTWF算法的信息增益.
3.2.1ID3算法及其对应生成的决策树
1)计算各个条件属性的信息增益

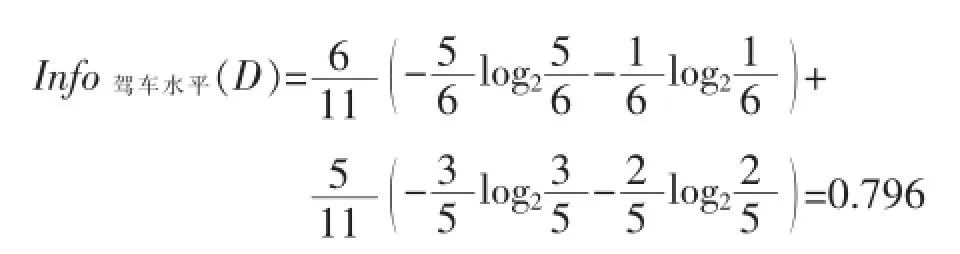
则相应属性的信息增益为:
Gain(喜欢的季节)=Info(D)-Info驾车水平(D)= 0.946-0.546=0.400
Gain(是否商务人士)=Info(D)-Info是否商务人士(D)= 0.946-0.796=0.150
Gain(收入)=Info(D)-Info收入(D)=0.946-0.591= 0.355
Gain(驾车水平)=Info(D)-Info驾车水平(D)=0.946-0.796=0.150
2)ID3算法生成的决策树
由以上各个属性的信息增益结果比较可知:Gain(喜欢的季节)>Gain(收入)>Gain(是否商务人士)=Gain(驾车水平)
因此,依照ID3算法分裂节点的原则将“喜欢的季节”属性作为决策树的根节点,对样本元组进行分类.对分类后形成的子集,用递归的方法对其计算熵值并进行分裂属性的选择,最终的得到的决策树如图1所示.
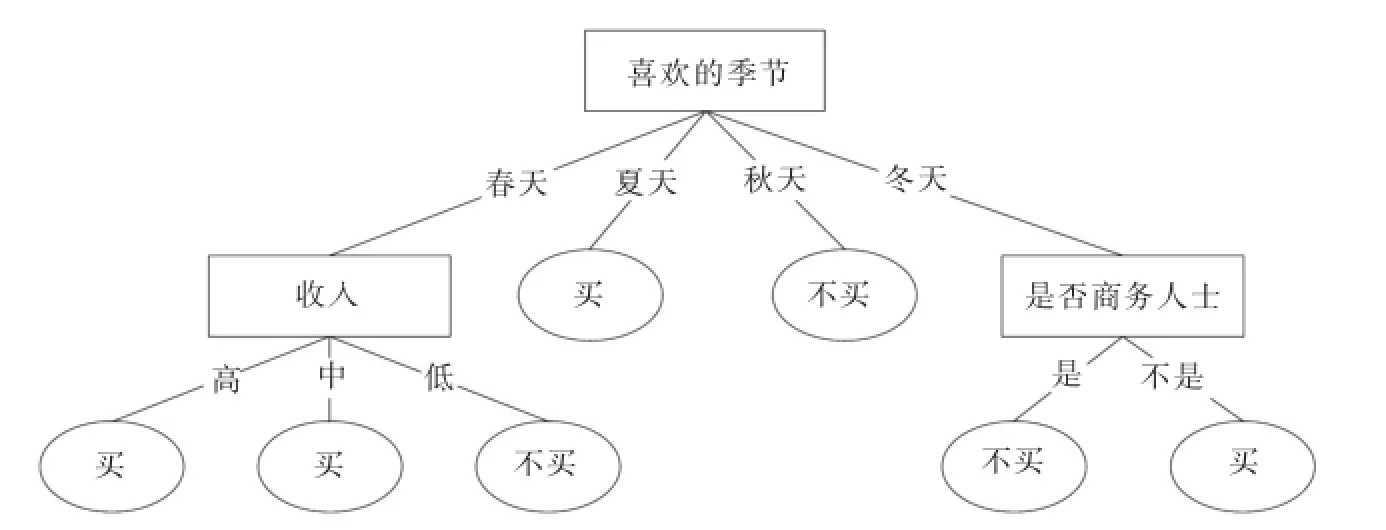
图1 ID3算法生成的决策树
3.2.2DTWF算法及其对应生成的决策树
首先根据ID3算法公式(1)计算每个条件属性的信息增益,并从中选出信息增益值最大的属性Ap;其次再找出属性取值个数最多的属性Aq;然后比较属性Ap和属性Aq是否相同,并根据比较结果计算出的权衡因子,最后根据公式(10)计算出在DTWF算法下属性Ap的信息增益.
1)信息增益值最大的属性Ap与属性取值个数最多的属性Aq之间的比较.
训练集D中信息增益值最大的属性为:A1“喜欢的季节”,而属性取值个数最多的属性为:Aq“喜欢的季节”,属性A1和属性Aq为同一属性,则属性A1具有多值偏向的趋势,因此需要使用权衡因子对属性A1的信息增益重新进行权衡.
2)计算属性Ap的权衡因子WF(Ap)
属性A1与决策类D所对应的DT_λ系数矩阵为:
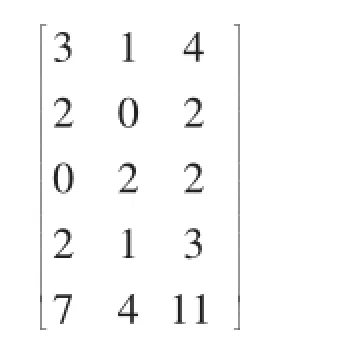
根据公式(8)可得属性A1的DT_λ(A1)值:
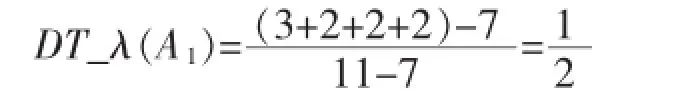
因此属性A1的权衡因子WF(A1)=DT_λ(A1)= 1/2,属性A1经过权衡因子权衡后得到新的信息增益为:
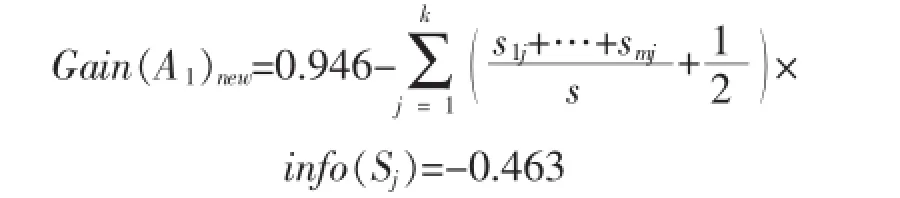
3)DTWF算法生成的决策树
将新属性增益Gain(A1)new与其他属性的信息增益进行比较可知:
Gain(收入)>Gain(是否商务人士)=Gain(驾车水平)>Gain(喜欢的季节)
因此将“收入”作为DTWF算法生成的决策树的根节点,对样本元组进行分类.对分类后形成的子集,用递归的基于权衡因子的方法对其计算熵值并进行分裂属性的选择,最终的得到DTWF算法生成的决策树如图2所示.
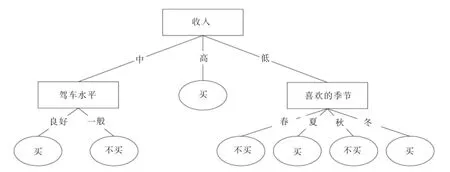
图2 D TWF算法生成的决策树
3.2.3DTWF算法的实例分析与总结
1)由图1和图2对比发现:在训练集D中,属性“喜欢的季节”属性值个数最多,ID3算法多值偏向的特点使其成为决策树的根节点.“喜欢的季节”是一种主观想法,不是购车的决定性因素,而在现实生活中,“收入”在一定程度上更能决定顾客是否购车.图2可看出,DTWF算法令“喜欢的季节”属性离决策树根结点的距离变远,降低其重要性;令“收入”属性作为决策树根结点,提高其重要性,符合实际情况,因此DTWF算法在一定程度上克服了多值偏向问题.
2)在决策树的构建过程中,区别于用户兴趣度算法中用户经验的主观参与,DTWF算法中的权衡因子是由训练集中属性之间客观的关系计算得到,因而权衡因子在一定程度上因无较多主观的参与或干扰从而避免了决策结果受用户主观思想的影响.
3.3实验验证及分析
3.3.1分类准确率和叶子节点数的比较
在表2提供的数据集进行实验数据测试,每一个数据集上进行10次试验.在分类准确率的实验结果中,去掉最大数据和最小数据,再求出平均分类准确率作为最终实验数据,可使实验结果具有普遍性.
将每一个数据集分成10个数据组,每个数据组中分别用ID3算法、文献[10]算法和DTWF算法构建决策树,每个数据组上均构建10次.在叶子节点数的实验结果中,去掉最大数据和最小数据,再求出平均叶子节点数作为该数据组的最终数据.每个数据集里以数据组为最小单位进行类似操作,求出其平均叶子节点数作为该数据集的最终实验数据.实验结果如表3:
从表3的实验结果中可看出:
1)在叶子节点数方面,ID3算法与文献 [6]算法、文献[9]算法实验所得结果近似.
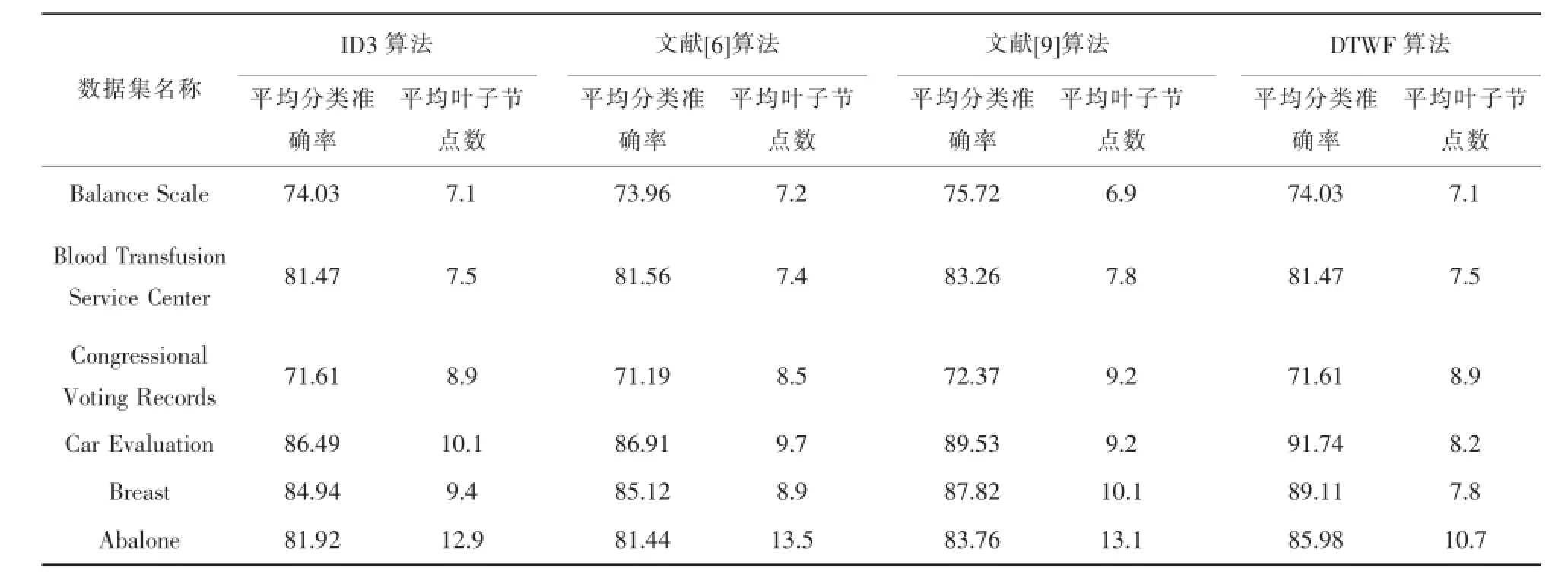
表3 实验结果
2)在分类准确率方面,文献[9]算法要优于文献[6]算法与ID3算法,而文献[6]算法与ID3算法实验所得结果近似.
3)当前3个数据集中属性取值个数相同时,DTWF算法与ID3算法在分类准确率和叶子节点数两个方面进行实验所的结果完全相同.产生这样结果的原因是:数据集中属性取值个数都相同,即不存在属性取值个数最多的属性,也不会产生多值偏向问题,因此无需使用权衡因子对某属性的划分权重进行权衡.
4)当后3个数据集中属性取值个数不相同时,DTWF算法具有较高的平均分类准确率和较少的平均叶子节点数.
3.3.2算法时间复杂度的分析比较
传统的ID3决策树构造方法,在构造每一层结点的时候,都需要对训练数据扫描一次,因此其时间复杂度为:O(n×s×log2s).文献[6]算法、文献[9]算法和本文提出的DTWF算法均在信息熵公式的基础上,通过采用改变子元组划分权重的方式,对ID3算法改进.因而文献[6]算法、文献[9]算法和本文提出的DTWF算法在复杂度数量级上还是不变,其时间复杂度也为:O(n×s×log2s).
3.3.3决策树生成时间的比较
在表2提供的数据集进行实验数据测试,分别对ID3算法、文献[6]算法、文献[9]算法和DTWF算法进行10次计算时间的测试,在实验结果中去掉最大数据和最小数据,再求出平均时间作为构建决策树模型所花费的时间,实验结果如表4.
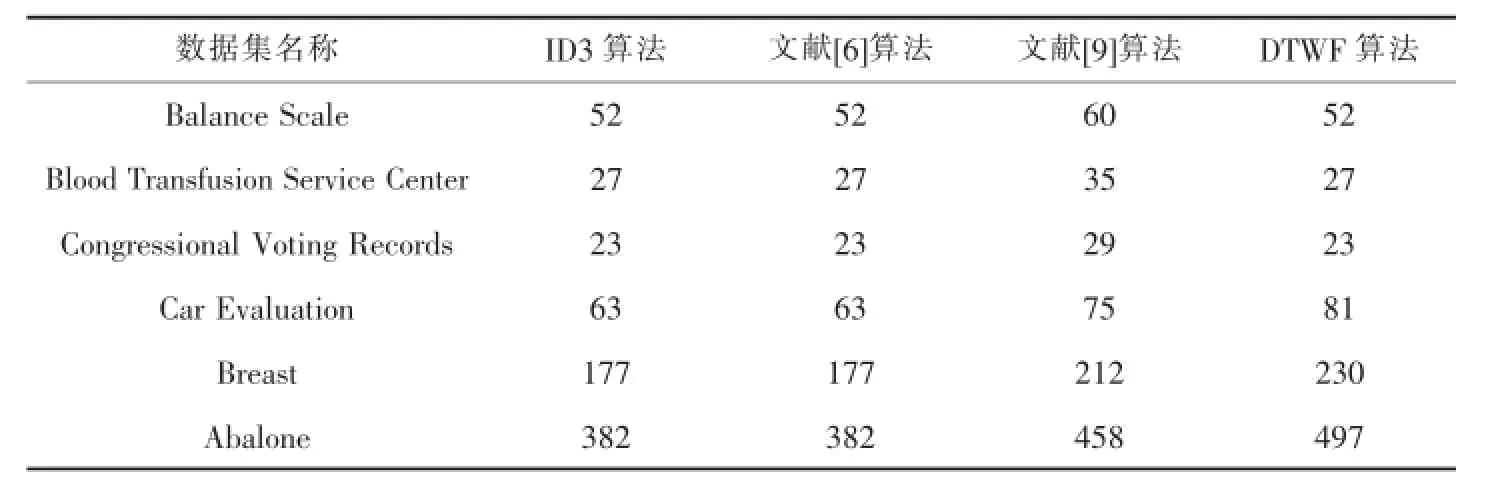
表4 算法建模速度比较/ms
从表4的实验结果中可看出:
1)从整体上看,ID3算法、文献[6]算法、文献[9]算法和DTWF算法构建模花费时间相差不大.
2)本文提出的DTWF算法在计算量上要略微复杂些,因此在构建决策树模型时,DTWF算法所花费的时间略多于其它算法.
3.4实验结论
结合图1、图2、表3和表4可看出:①本文提出的DTWF算法可以克服多值偏向问题.②相比于ID3算法,文献[6]的改进算法虽能克服多值偏向问题,但在分类准确率和叶子节点数这两个方面没有明显改进,改进后ID3算法的效率未得到提高;②在时间复杂度上的数量级上,DTWF算法和ID3算法保持一致;在计算量上,DTWF算法要比其它三种算法要略微复杂些,因此DTWF算法决策树建模所花费的时间略多于其它算法;从整体上看,DTWF算法与其它算法构建模花费时间相差不大.④当数据集中属性取值个数相同时,即不存在多值偏向的趋势时,本文提出DTWF算法与ID3算法相同;当数据集中属性取值个数不相同时,即存在多值偏向的趋势时,与ID3算法、文献[6]算法和文献[9]算法相比较,本文提出DTWF算法具有较高的分类准确率,在算法生成决策树规模上,DTWF算法也要优于其它算法,因为DTWF算法具有更少的叶子节点数,此外还能克服ID3算法的多值偏向问题.
4 结束语
本文结合λ相关系数提出了DTWF算法,根据属性之间的依赖关系得到属性的权衡因子,通过用权衡因子代替依赖先验知识的用户兴趣度参数,以克服ID3算法的多值偏向问题.DTWF算法首先通过判断数据集是否存在多值偏向趋势,继而客观地计算出属性的权衡因子;然后再根据得到的权衡因子对某属性的子元组划分权重进行重新权衡,并将用DTWF算法得到的新信息增益与其它属性的信息增益进行重新比较;最后从中选取具有最大信息增益值的属性作为分裂属性.DTWF算法既不受属性取值个数的影响,也不要求用户需要先验知识或领域知识,又能避免决策结果受到主观因素的干扰和影响.实验结果分析表明,相比于原ID3算法以及文献[6]基于用户兴趣度的改进算法,当数据集中存在多值偏向的趋势时,DTWF算法具有更高的平均分类精确度和较少的平均叶子节点数.UCI上大部分数据集的属性取值个数基本不相同,属性取值个数相同的情况占少数,因此在大部分情况下,DTWF算法要优于ID3算法和文献[6]算法及其相关类似改进算法.
[1]朱明.数据挖掘[M].中国科学技术大学出版社,2002:67-68.
[2]韩家炜,堪博.数据挖掘概念与技术[M].2版.机械工业出版社,2007:188-189.
[3]Quinlan J R.Induction of decision trees[J].Machine learning,1986,1(1):81-106.
[4]王苗,柴瑞敏.一种改进的决策树分类属性选择方法[J].计算机工程与应用,2010,46(8):127-129.
[5]王永梅,胡学钢.决策树中ID3算法的研究[J].安徽大学学报(自然科学版),2011,35(3):71-75.
[6]曲开社,成文丽,王俊红.ID3算法的一种改进算法[J].计算机工程与应用,2003,39(25):104-107.
[7]刘建粉,史永昌.基于用户兴趣分类优化的聚类模型仿真[J].微电子学与计算机,2014,31(5):171-174.
[8]王永梅,肖中新.改进决策树算法在水环境质量评价中的应用[J].合肥学院学报(自然科学版),2014,24(1):35-39.
[9]叶明全,胡学钢.一种基于灰色关联度的决策树改进算法[J].计算机工程与应用,2007,43(32):171-173.
[10]王建伟,王鑫,许宪东,等.改进的ID3算法在远程教学系统中的应用[J].黑龙江工程学院学报,2014,28(1):67-70.
[11]梁前德.统计学[M].2版.北京:高等教育出版社,2008.
[12]朱颢东.ID3算法的改进和简化[J].上海交通大学学报,2010(7): 883-886.
[13]喻金平,黄细妹,李康顺.基于一种新的属性选择标准的 ID3改进算法[J].计算机应用研究,2012,29(8):2895-2898.
[14]解亚萍.基于统计相关系数的数据离散化方法[J].计算机应用,2011,31(5):1409-1412.
[15]Hu X,Cercone N.Data mining via generalization,Discrimination and rough set feature selection[J].Knowledge and Information System:An International Journal,1999,1(1):21-27.
[16]武丽芬.改进的决策树算法在文理分科中的应用研究[J].微计算机应用,2011,32(8):7-12.
Optimized algorithm of decision tree based on weighting factor
DONG Yuehua,LIU Li
(School of Information Engineering,JiangxiUniversity of Science and Technology,Ganzhou 341000,China)
Through the analysis of the issues ofmultivalue bias in the ID3 algorithm and subjectivity of the optimized traditional ID3 algorithm,an improved algorithm of decision tree based on weighting factor is put forward.The new algorithm introduces the weight factor that reflects the mutual relationship between the attributes.The ID3 algorithm is improved by redistricting the weight of attributes which hasmost values.The experiments on UCIdata sets show that the optimization ID3 algorithm can overcomemultivalue bias when the values of different attributes in data set are not the same.This algorithm not only improves the accuracy of average classification,but also reduces the number of average leaf nodes in the process of constructing a decision tree.
ID3 algorithm;multivalue bias;weighting factor;decision tree;weight
TP301.6
A
2095-3046(2015)05-0090-08
10.13265/j.cnki.jxlgdxxb.2015.05.016
2015-04-13
国家自然科学基金资助项目(71061008)
董跃华(1964-),女,副教授,主要从事数据挖掘、软件工程、软件测试等方面研究,E-mail:4490367@qq.com.

