一种结合灰狼优化和K-均值的混合聚类算法
杨红光, 刘建生
(江西理工大学理学院,江西赣州341000)
一种结合灰狼优化和K-均值的混合聚类算法
杨红光,刘建生
(江西理工大学理学院,江西赣州341000)
针对传统K-均值聚类算法对初始中心选择敏感和全局搜索能力不足的缺点,提出一种结合灰狼优化和K-均值的混合聚类算法 (GWO-KM).将灰狼优化智能算法首次应用到聚类分析领域,利用灰狼算法良好的勘探能力去寻找使聚类结果最佳的一组聚类中心,克服了原始聚类算法对初始中心点的过度依赖.通过在UCI标准数据集上的仿真实验表明,该混合聚类算法相对于传统的K-均值聚类算法和其他改进算法,在收敛速度、聚类质量和稳定性上都表现更佳.
聚类分析;K-均值聚类算法;灰狼优化算法
0 引言
“物以类聚,人以群分”是对分类学的一个概括,里面的“类”是指一些特征相似的对象组成的集合.无论在现实生活中还是在科学研究领域,分类问题可谓无处不在.以前的分类只能凭借个人经验来完成,得到的分类结果并不十分准确,随着科学技术的发展,对于分类的要求越来越高,传统的分类已不能满足科学需求.如今,随着数学工具和多元统计方法被应用到分类学中,渐渐地在数值分类学中形成了新的分支 “聚类分析”[1].目前聚类分析在很多研究领域都得到了广泛应用,像机器学习、数据挖掘、生物信息学、数字图像的自适应修复[2]等都用到了聚类分析技术.
K-均值聚类是由Mac Queen提出的一种非常经典的非监督实时聚类算法[3-4],它的基本思路是在一定的相似性度量准则(距离)基础上将数据划分到最近或相近的聚类中心形成预定的类簇[5].其原理非常简单,当处理的数据量很大时比较方便,但是它对于初始中心点的选择非常敏感,容易陷入局部最优解.
灰狼优化算法(GWO)是Mirjalili S等[6]于2012年通过模拟自然界中灰狼种群捕食的过程提出的一种新的元启发式算法.目前,国外学者GM Komaki等将GWO算法应用于两级流水车间调度问题中[7],N Muangkote等用GWO算法训练高斯径向基函数网络[8].国内学者Aijun Zhu等将GWO用在了芯片系统的3D Stack技术[9]上.本文将GWO算法首次应用在聚类分析领域,利用它良好的勘探与开发能力来优化K-均值聚类,通过实验对比显示出这种新的混合聚类算法良好的聚类能力.
1 K-均值算法原理
K-均值聚类算法是以最小化误差函数为基础,将数据X={x1,x2,…,xn}划分到K个类簇C={c1,c2,…,ck}中[1].
算法的运行过程如下[10]:
Step1给定类数K;
Step2在X={x1,x2,…,xn}(其中xi为d维向量)中随机取K个对象作为初始聚类中心;
Step3分别计算每个数据对象xi到所有聚类中心点的距离d(xi,cj),然后根据相似性准则将对象划分到与其距离最近的类;
Step4以每个类簇中所有对象的均值作为新的聚类中心;
Step5计算聚类的目标函数值,当误差函数值的变化很小或者算法达到最大迭代次数时,结束聚类进程,否则重复Step3~Step5过程.
目标函数选用基于划分的聚类分析的衡量准则函数J,J表示所有的类内距离之和

K-均值聚类算法的原理简单,收敛速度较快,但是由于在选择初始聚类中心时采用随机机制,因为初值选择的不同时常会得到数值很大的聚类结果,这说明算法的稳定性很低,而且容易陷入局部最优.
近些年,对于群体智能算法的研究越来越深入,将智能算法用在聚类当中的例子也有很多.文献[11]用免疫粒子群算法对K-均值聚类进行优化,文献[12]将遗传算法与K-均值聚类进行了结合.这些智能算法都在一定程度上对K-均值聚类算法做了改进,但在稳定性或收敛速度等方面仍有待提高.
2 灰狼优化算法(GWO)
灰狼优化算法是一种新的元启发式算法[6],它的灵感来自于自然界中的灰狼种群.2012年Mirjalili S通过模拟自然界中灰狼种群的等级层次机制和狩猎行为提出.
2.1等级层次
灰狼是一种群居的顶级掠食者,在种群中它们的社会等级层次被分为α、β、σ、ω四层.α是狼群的领导者,β是下属的狼,σ它负责帮助做决策或其他活动,ω是最底层的狼.服从于、但是又控制.根据文献[13],狼群的狩猎过程被描述为:跟踪,追逐,接近猎物;追赶包围,骚扰猎物直到它们停下;攻击.整个狼群内部等级层次机制的描述如图1所示.
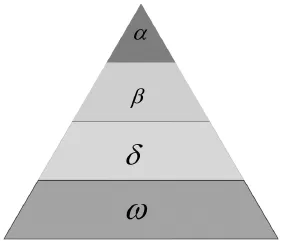
图1 狼群等级层次机制
2.2数学模型和算法
在GWO算法中狩猎行为(优化操作)主要由灰狼α、β和δ引导,而灰狼ω跟随着这三者[6].
2.2.1包围猎物
灰狼在狩猎的时候要包围猎物,为了描述这种行为,Mirjalili S提出了下面的数学公式:

其中,t表示当前的迭代,→A和→C是系数向量,→Xp是目标的位置向量.→X表示一只灰狼的位置向量.→A和→C由下面的公式得出:

2.2.2狩猎
灰狼有能力识别猎物的位置并包围他们.狩猎通常是由α引导,β和δ偶尔也可能参与狩猎.为了以数学模式模拟狩猎行为,假设α,β和δ更有能力了解潜在的猎物的位置.因此,保存到目前为止获得的前三个最好的解,并迫使其他的灰狼(包括ω)根据这些狼的位置来更新它们的位置,可由公式(6)~式(8)表示:
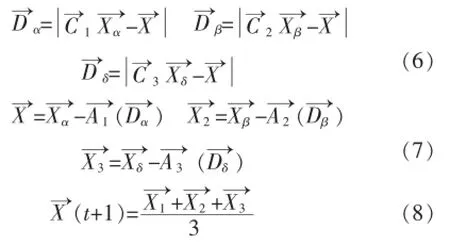
2.2.3攻击猎物(开发)
当猎物停止移动时,狼群会进行攻击来完成狩猎活动.为了在数学模式上靠近猎物设定减小→a的值,这样→A的波动范围也因为→a下降了.换句话说,在迭代过程中,当a的值从2到0下降时,→A是在[-a,a]内的一个随机值.当→A的值在[-1,1]内时,灰狼的下一个位置可以是它现在的位置和猎物的位置之间的任意位置.当<1时,狼群向猎物攻击.
2.2.4搜索猎物(勘探)
灰狼主要是根据α,β,δ的位置来搜索猎物.他们互相分散去寻找猎物然后聚集在一起去攻击猎物.为了在数学形式上模拟分散,利用随机的大于1或者小于-1的→A的值来迫使灰狼偏离猎物,这样可以加强算法的勘探能力使GWO算法实现全局搜索.当>1时迫使灰狼偏离猎物,借此希望找到一个合适的猎物.在GWO算法中利于勘探的另一成分是→C.在公式(5)中可以看到,向量→C随机的包含在[0,2]中.这一成分的设置提供给猎物随机的权值是为了随机的强化或弱化猎物在定义的距离方程中的影响,这能帮助GWO算法在优化的过程中展现更多的随机行为.有利于勘探和避免全局最优.值得一提的是,和A相比C不是直线减小的.在这里要求C一直是随机的是为了不仅在初始迭代中,而且在最后的迭代过程中也一直加强搜索.这一成分在遇到局部优化停滞不前时很有用,尤其是在最后的迭代过程中.
3 结合GWO和K-均值的混合聚类算法
K-均值聚类算法的目标是寻找一组能够让所有对象的类内距离之和达到最小值的聚类中心,而GWO算法的实质是一个能够实现全局寻优的群体智能算法.结合GWO和K-均值的混合聚类算法是利用GWO算法较强的全局搜索能力和能够跳出局部最优的特点寻找一组使聚类目标函数值最小的中心点,这在一定程度上减弱了原始K-均值聚类对初始中心点的过度依赖.
结合GWO和K-均值的混合聚类算法在搜寻全局最优聚类中心时使用一组候选解执行优化操作,通过GWO算法的公式(6)~公式(8),以当前取得的适应度值最佳的前三名灰狼的位置为基础来更新其他灰狼的位置,整个狼群在迭代过程中不断地进化,会逐渐向猎物靠近,直到算法迭代结束返回最优解.
分类的目标是要做到划分尽可能的准确,相似度高的对象都能分到同一个类中.聚类的精度越高,它们的目标函数值越小.而灰狼优化算法中适应度函数的设定会影响整个狼群的进化行为.为了与灰狼优化算法里“保留适应度值最大的前三名灰狼”的操作做对应,在这里将K-均值聚类算法的目标函数与灰狼优化算法的适应度设置做了结合,定义灰狼优化算法的适应度函数fit如公式(9)所示:

通过公式可以看出当得到的聚类越准确,聚类的目标函数值就会越小,而灰狼的适应度函数值就会越大.不断地更新狼群的中的α、β和δ,最终取迭代操作完成后得到的最大适应度的灰狼α,α代表的聚类中心点集即为整个数据集的最佳聚类中心.利用灰狼优化算法较好的全局寻优能力搜寻所有对象中最佳的聚类中心,避免了原始K-均值聚类对于初始聚类中心点的过度依赖,而且通过公式(4)和公式(5)可以看出,GWO算法中定义的算子a和→C能够有效的避免算法由于陷入局值导致的停滞不前.
在GWO中,搜索过程开始于随机的创建一个狼群,在进行迭代时,用α,β,δ狼来预估猎物的位置,其他的灰狼通过更新公式不断地接近目标并分散到目标周围.本文提出的结合灰狼优化和K均值的混合算法具体实现的过程为:GWO在产生初始狼群时,让每一只灰狼代表一个聚类中心点集的划分,将GWO的适应度函数fit设定为与K-均值聚类算法的衡量准则函数相关的函数,经过不断地迭代返回适应度最优的灰狼α,α代表的聚类中心点集就是使K-均值聚类的类内距离和最小的解.然后以这组聚类中心进行K-均值聚类得到最优的聚类效果.
GWO-KM算法描述如下:
Step1初始化操作
给定数据集X(x1,x2,…,xn),其中xi为d维向量;
初始化a,A,C;
给定聚类个数K.
设定最大迭代次数T.
产生初始狼群G(G1,G2,…,GM),每一只灰狼都代表着一种聚类的划分,狼群由公式(10)产生:

Step2计算适应度
计算每只灰狼的适应度,并保留适应值最大的前3只灰狼:

在这里Gα、Gβ和Gδ分别表示适应度值最大的灰狼和适应度值第二与第三的灰狼.
Step3灰狼位置的更新操作
当t<设定的最大迭代次数,通过公式(8)对每一只灰狼进行位置上的更新.
Step4更新参数
更新a,A,C.
重新计算每只灰狼的适应度值,从而更新Gα、Gβ和Gδ,迭代数t+1.
Step5若达到最大迭代数Gα,返回,否则继续执行Step2~Step5直至结束.
4 实验仿真与分析
为了验证本文提出的算法的有效性,应用相同的数据集,与原始K-均值聚类算法、文献[11]提出的免疫K-均值算法、文献[12]提出的遗传谱聚类算法的实验结果,在算法的收敛时间、聚类结果的最大值与最小值、平均值以及标准差五个方面进行了实验比较.
4.1仿真环境和仿真数据
仿真的硬件环境:AMD phenom CPU 2.6 GHz,内存为4 GB,软件为MATLAB 2010b.实验所用的数据来自于UCI数据库中比较有代表性的wine和iris数据集.
UCI数据库是专门用于学习人工智能和机器学习的数据库,是做测试分类和聚类算法的常用数据库[14],每一个数据集都有明确的类数,这样对于检验算法的性能,计算聚类的错误率很有帮助.其中iris是基于不同的鸢尾花的特征作为数据来源. iris数据集里有150个具有4种属性的数据样本,分为3类,每一类中包含50个样本,它的分类特性较为明显.wine是基于不同葡萄酒的特征作为数据来源,数据包含178个具有13个属性的样本,分为3类.属性之间存在交叉情况,导致它的分类特性并不是特别明显.
4.2实验结果分析
GWO-KM算法实验设置灰狼种群为规模为30只,算法的最大迭代次数T=500次.实验结果中的收敛时间(单位为s)和标准差是通过50次单独实验得出结果后,取它们的平均值做记录.

表1 iris数据集实验结果

表2 w ine数据集实验结果
由表1和表2可以看出,原始K-均值聚类算法虽然收敛速度很快,但是它的聚类结果会因为选择不同的初始聚类中心而出现比较大的差距.得出较差的结果说明其陷入了局部最优,显示出它的全局搜索能力一般.遗传优化谱聚类算法与其他的算法相比较,很明显其收敛速度太慢耗时太长是其一大缺陷,而且实验得出的标准差较大,这说明算法的稳定性也有待改善.免疫粒子群K-means与原始K-均值聚类算法和遗传谱聚类相比,在算法稳定性、收敛时间和精度上都有了一定的提升,但是和本文提出的GWO-KM算法相比,GWO-KM算法明显在收敛速度上优于它,而且在聚类精度上也有提升.GWO算法因为具有比较平衡的勘探与开发能力,而且算法的目标就是找到一组最佳的聚类中心,这使得K-均值聚类减少了对初始中心的依赖,并且在迭代过程中它的勘探算子能够使算法避免陷入局值,从而可以得到比较理想的结果.两组数据的实验结果显示,GWO-KM算法的得到的标准差都是0,表明这种算法具有较高的稳定性.
综上所述,这种结合灰狼优化和K-均值的混合聚类算法(GWO-KM)在收敛速度、聚类精度和稳定性上与原始的K-均值聚类以及文献[11]和文献[12]的算法相比,都有一定的优势.它克服了K-均值聚类过度依赖初始聚类中心容易陷入局部最优解的缺陷、稳定性强、并提高了聚类的质量.
5 结束语
本文将一种新的智能算法应用到聚类分析领域,提出了一种结合灰狼优化和K-均值的混合聚类算法.利用灰狼优化算法良好的勘探与开发能力解决了K-均值聚类算法对于初始聚类中心的过度依赖和易陷入局值的缺点.与原始的聚类算法以及几种结合智能算法的改进算法比较,该算法具有较快的收敛速度和较好的聚类质量.
[1]梁烨炜.K-均值聚类算法的改进及其应用[D].长沙:湖南大学,2012.
[2]尹宝勇,刘慧,刘建生.基于改进FCM和径向基函数插值的图像修复[J].江西理工大学学报,2014,35(3):73-78.
[3]李梓,于海涛,贾美娟.基于改进模拟退火的优化K-means算法[J].计算机工程与应用,2012,48(24):77-80.
[4]罗可,蔡碧野,吴一帆,等.数据挖掘中聚类的研究[J].计算机工程与应用,2003,39(20):182-184.
[5]王慧,申石磊.基于改进的K均值聚类彩色图像分割方法[J].电脑知识与技术,2010,6(4):962-964.
[6]Mirjalili S,Mirjalili S M,Lewis A.Grey wolf optimizer[J]. Advances in Engineering Software,2014,69(3):46-61.
[7]Komaki G M,Kayvanfar V.Grey wolf optimizer algorithm for the two-stage assembly flow shop scheduling problem with release time[J].Journal of Computational Science,2015:109-120.
[8]Muangkote N,Sunat K,Chiewchanwattana S.An improved grey wolf optimizer for training q-Gaussian Radial Basis Functionallink nets[C]//Computer Science and Engineering Conference(ICSEC),2014 International.IEEE,2014:209-214.
[9]Zhu A,Xu C,Li Z,et al.Hybridizing grey wolf optimization with differential evolution for global optimization and test scheduling for 3D stacked SoC[J].Journalof Systems Engineering and Electronics,2015,26(2):317-328.
[10]李翠,冯冬青.基于改进K-均值聚类的图像分割算法研究[J].郑州大学学报,2011(1):109-113.
[11]郑晓鸣,吕士颖,王晓东.基于免疫粒子群优化的聚类算法[J].计算机工程,2008,34(15):179-181.
[12]王会青,陈俊杰,郭凯.遗传优化的谱聚类方法研究[J].计算机工程与应用,2011,47(14):143-145.
[13]Muro C,Escobedo R,Spector L,et al.Wolf-pack(Canis lupus)hunting strategies emerge from simple rules in computational simulations[J].Behavioural Processes,2011,88(3):192-197.
[14]汪中,刘贵全,陈恩红.一种优化初始中心点的K-means算法[J].模式识别与人工智能,2009,22(2):299-304.
A hybrid clustering algorithm based on Grey Wolf Optimizer and K-means algorithm
YANG Hongguang,LIU Jiansheng
(Faculty of Science,JiangxiUniversity of Science and Technology,Ganzhou 341000,China)
Considering the disadvantages of K-means Cluster Algorithm,such as inadequacy for global search and being sensitive to initial cluster centers,this paper proposes a hybrid clustering algorithm based on Grey Wolf Optimizer and K-means(GWO-KM).Grey Wolf Optimizer is applied in the field of cluster analysis for the first time.With its good ability of exploration,the new intelligent algorithm helps K-means cluster find a set of cluster centers which can get the best clustering result,thus avoiding the original algorithm's overdependence on initial centers.The experiments based on UCI show that,the hybrid algorithm can result in faster convergence speed,higher accuracy,and greater stability,compared with traditional k-means algorithm and other improved algorithms.
cluster analysis;K-means;Grey Wolf Optimizer
TP18
A
2095-3046(2015)05-0085-05
10.13265/j.cnki.jxlgdxxb.2015.05.015
2015-06-24
国家自然科学基金项目资助(61462036)
杨红光(1990-),男,硕士研究生,主要从事数字图像处理等方面的研究,E-mail:921195515@qq.com.
刘建生(1975-),男,副教授,主要从事智能计算与通信安全和图像处理等方面的研究,E-mail:jxgzjscn@126.com.

