一种应用精英混沌搜索的函数优化算法
井福荣, 郭肇禄, 罗会兰(江西理工大学,.信息工程学院;.理学院,江西 赣州341000)
一种应用精英混沌搜索的函数优化算法
井福荣a,郭肇禄b, 罗会兰a
(江西理工大学,a.信息工程学院;b.理学院,江西 赣州341000)
针对基本FPA算法在求解复杂工程优化问题时存在收敛速度慢的缺点,提出应用精英混沌搜索的花粉授粉算法(CSFPA).CSFPA算法在搜索过程中从当前种群中随机选择出一个个体,对其执行精英混沌搜索操作,从而加快算法的收敛速度.将提出的CSFPA算法与基本FPA算法在几个国际上常用的基准测试问题上进行了比较实验,实验结果表明CSFPA算法能够在大多数测试问题上比基本FPA算法获得更优的结果.
优化算法;演化算法;混沌搜索;花粉授粉算法
0 引言
函数优化问题的优劣直接影响科学研究的成败,因此在现代科学研究中有着十分重要的地位.花粉授粉算法[1](Flower pollination algorithm,FPA)是2012年由剑桥大学学者Yang提出的一种新的系统优化算法,该算法基于模拟现实世界中植物花朵授粉过程而提出.一般而言,花粉授粉有异花授粉(cross-pollination)和自花授粉(self-pollination)两种形式,异花授粉是通过昆虫采粉作为传播方式,实现雌性花朵和雄性花朵之间相对远距离的授粉,也即交叉授粉.由于昆虫飞行距离相对较远,因此异花授粉可以在较远距离发生,这种方式也称之为全局授粉.自花授粉是植物成熟的花粉粒传到自身的柱头上或同一种植物的不同花朵上进行授粉的过程.相对而言自花授粉也称之为局部授粉.基于上述思想,FPA算法对以上两种授粉方式分别设计了交叉授粉算子和自花授粉算子来求解优化问题,同时得到广大学者、研究人员的关注.
由于花粉授粉算法在求解优化问题过程中,也存在一些收敛速度慢等缺点,研究人员提出了许多改进的FPA算法,并在相关研究领域的应用中取得了很好的效果.Yang等应用FPA算法(MOFPA)[2]进行多目标问题的求解,其做法是通过随机权数把多个优化问题变换成单一问题来进行求解,在4组及以上优化问题基准测试的实验结果表明提出的MOFPA算法能够很好解决多目标优化问题.Wang等[3]为了提高FPA的运算效率及性能提出了一种优化FPA算法 (DDIFPA).DDIFPA结合逐维搜索策略和邻域搜索策略,提高了算法在搜索最优解的速度和解的质量.标准测试函数的实验表明DDIFPA具有明显的搜索性能优势.Prathiba等[4]成功将FPA算法应用于求解经济负荷分配问题中,取得了良好的效果.Abdel-Raouf等[5]将FPA融合到粒子群优化算法(PSO)中,提出了一种混合FPA算法 (FPPSO),并应用于求解约束优化问题中;Chakraborty等[6]将FPA融合到差分进化算法中,提出了一种花粉授粉混合算法(DE-FPA);Rodrigues等[7]提出了二进制FPA算法(BFPA),并有效地解决了求解特征选择问题;Dubey等[8]为了求解经济调度问题,提出了一种生物学启发的改进FPA算法(MFPA),在MFPA算法中,通过使用一个参数进行搜索步长的调节,该参数可大可小以便提高搜索效率和精确度.同时引入了一个可在全局范围内进行最优解局部搜索的搜索参数.肖辉辉等[9]为了减少FPA算法陷入局部最优值的概念,将模拟退火的思考融合到FPA算法.接着,肖辉辉等[10]为了提高FPA算法的局部搜索能力,将复合形法引入到花粉授粉算法中.井福荣等[11]将反向学习策略融合到FPA算法,以此提FPA算法的搜索性能.
综上所述,FPA是一种性能优越的智能优化算法,在工程优化问题的求解中具有一定优势.但国内外对FPA的研究还刚刚兴起,FPA算法的性能提高还有很大的空间,本文针对基本FPA算法在解决复杂优化工程实践问题时存在着收敛速度慢的缺点[8],将精英混沌搜索策略引入到FPA算法中,提出了一种应用精英混沌搜索的花粉授粉算法(CSFPA).在CSFPA算法的搜索过程中,从当前种群中随机选择出一个个体,对其执行精英混沌搜索操作,从而加快算法的收敛速度.在数值实验中,利用一些演化计算领域中广泛使用的基准测试函数做了比较实验,实验结果验证了CSFPA算法的有效性.
1 花粉授粉算法
由于现实世界中的花粉授粉过程是一个极其复杂的生理过程.使用计算机完全实现花粉授粉过程将导致非常高的时间复杂度,因此FPA算法只是对花粉授粉过程的核心思想进行模拟.
首先花粉授粉算法随机产生一个含有NP个个体的种群P(t)={Xti}用于算法的初始化,其中Xti=[xti,1,xti,2,…,xti,j,…,xti,D],j=1,2,…,D;i=1,2,…,NP,NP为种群大小,D表示求解问题的维数,t代表当前进化代数[1].其次,该算法一直循环执行交叉授粉和自花授粉两个过程直到达退出条件为止.
在算法的执行过程中,FPA以初始值Pc大小计算异花授粉过程,之后以1-Pc的大小计算自花授粉过程[1].其中异花授粉按照如下公式计算[2]:
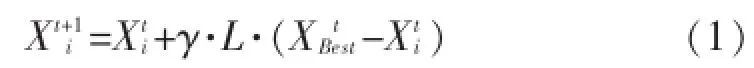
其中γ为缩放参数,一般建议设定其值为0.1[2];L是一个随机值,它服从指数为λ的Levy分布,一般建议设定其值为1.5[2],XtBest代表局部最优解.
自花授粉按照如下公式计算[2]:

其中ε∈[0,1],并服从均匀分布,随机整数j,k∈[1,NP],并且满足i≠j≠k.
FPA算法流程描述如图1所示.在该算法中,首先随机产生初始种群,评价每个个体的适应值,然后循环执行演化操作直到满足终止条件.在演化操作循环中,首先定义随机实数rp∈[0,1]并服从均匀分布,当rp<Pc时,则按公式(1)执行交叉授粉操作算子,否则按公式(2)执行自花授粉操作算子,然后再执行选择算子选择出优胜个体进入下一代种群.
2 CSFPA算法
FPA已经成功应用到了一系列复杂工程优化问题的求解中,并且获得了满足实际工程需求的优化结果.然而在工程实践中,研究人员发现基本FPA在求解高维、非线性等特性的复杂工程优化问题时往往容易出现收敛速度慢的缺点,其主要原因是复杂工程优化问题的搜索空间随着问题维数的增长呈指数规模增长,面对着这种情形,基本FPA算法的局部搜索能力往往表现不足,从而导致算法很难有效地朝着全局最优解的方向进行搜索,无法逼近全局最优解[10].为了进一步提高基本FPA算法的局部搜索能力,加快求解高维、非线性等特性的复杂工程优化问题的收敛速度,将精英混沌局部搜索策略融合到基本FPA算法中,形成一种应用精英混沌搜索的花粉授粉算法(CSFPA),在搜索过程中从当前种群中随机选择出一个个体,对其执行精英混沌局部搜索操作,从而有效地增强算法的开采能力,加快收敛速度.

图1 基本FPA算法的流程图
2.1CSFPA的精英混沌搜索
混沌现象是自然界中广泛存在的一种非线性系统,它具有遍历性和初始值敏感性的特点[12].利用混沌系统的这些特点,给定一个随机初始值,设定足够长的时间,混沌系统可以按照自身的运动规律,随机遍历系统内的所有状态[13].许多研究人员将混沌系统的这种特性融合到智能优化算法中,利用混沌运动规律来进行局部搜索,从而加快算法的收敛速度,其中文献[14]提出了一种带有收缩机制的混沌搜索算子,该混沌搜索策略一方面利用混沌系统的遍历性和初始值敏感性的特点,在当前种群的搜索区域内混沌采样产生新个体,然后再将新个体与最优个体进行线性组合生成一个试验个体,然后将试验个体与最优个体进行竞争,淘汰两者中的较差个体,保留优胜个体.在传统混沌搜索算子[14]的基础上,进一步提高其局部搜索能力,提出精英混沌搜索策略,利用种群中的优质个体所含的经验信息来引导搜索方向,进而加快算法的收敛效果及速度.
就具体精英混沌搜索算法的操作过程而言,通过随机选择确定一个个体Xr,再根据巴特莱法则[15]从当前种群中选择出前20%的精英个体,并计算出所选择的精英个体的搜索区域的上界CA和CB下界:

在计算出当种群中的精英个体的搜索上下界后,随机产生一个混沌初始值K1,如果混沌初始值等于0.25,0.5或0.75,则重新产生直到它不等于0.25,0.5或0.75[14]:
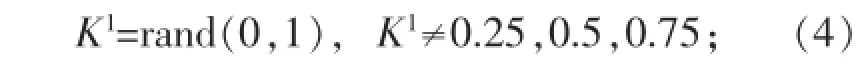
在以后的每一次混沌搜索迭代中,混沌因子按Logsig混沌映射计算[14]:
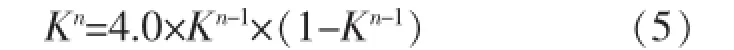
其中n为本次混沌搜索的当前迭代次数,在得到混沌因子后Kn,则按以下公式产生一个新个体:

其中a为[0,1]之间的随机数,它决定着Xr个体与精英混沌搜索个体之间的权值;在计算出个体Un后,如果Un比Xr更优,则用Un替换Xr,并停止执行精英混沌搜索操作,否则保持Xr不变成,并一直执行精英混沌搜索操作直至迭代次数达到预先设定的最大次数.
2.2CSFPA的总体流程
为了提高基本FPA算法在求解复杂工程优化问题时的收敛速度,将精英混沌局部搜索策略融合到基本FPA算法中,增强基本FPA的局部搜索能力.在CSFPA的搜索过程中,首先随机选择出一个个体,再找出当前种群中的精英个体,并计算所找到的精英个体的搜索上下界,然后利用精英个体的有益信息以及混沌系统的遍历性和初始值敏感性的特点在搜索空间中不断产生新个体,从而在一定程度上提高算法的收敛速度.下面给出CSFPA算法具体实现过程,如下面算法所示.
算法:应用精英混沌搜索的FPA算法(CSFPA).
Step1:设置D,NP,Pc;Step2:当前迭代初始值t=0,评判初始值FEs=0;Step3:对种群进行初始化,对个体的适应值进行评判,设FEs=NP;
Step4:是否满足终止条件?Step16:Step5;Step5:执行基本FPA的计算步骤;Step6:随机选择出一个个体Xr;
Step7:从当前种群中选择出前20%的精英个体,并按公式(3)计算选择的精英个体的搜索区域的上界和下界;
Step8:n=1;
Step9:按公式(4)产生混沌因子初始值;
Step10:按公式(6)对Xr执行精英混沌搜索得到个体Un,并计算Un的适应值;
Step11:如果Un比Xr更优,则用Un替换Xr,并转到Step15;否则转到Step12;
Step12:n=n+1;
Step13:按公式(5)计算新的混沌因子;
Step14:如果n小于D/5,则转到Step 10;否则转到Step 15;
Step15:t=t+1,转到Step4;
Step16:输出最优解,CSFPA算法结束.
3 数值实验
3.1实验设置
为了检验CSFPA算法是否有效,本文选择了10个Benchmark测试函数对算法CSFPA进行性能分析.10个Benchmark测试函数的特性在表1中给出了详细描述[16,17].其中f1-f4为单峰函数,f5-f10为多峰函数,10个测试函数的维数 D都为30维.
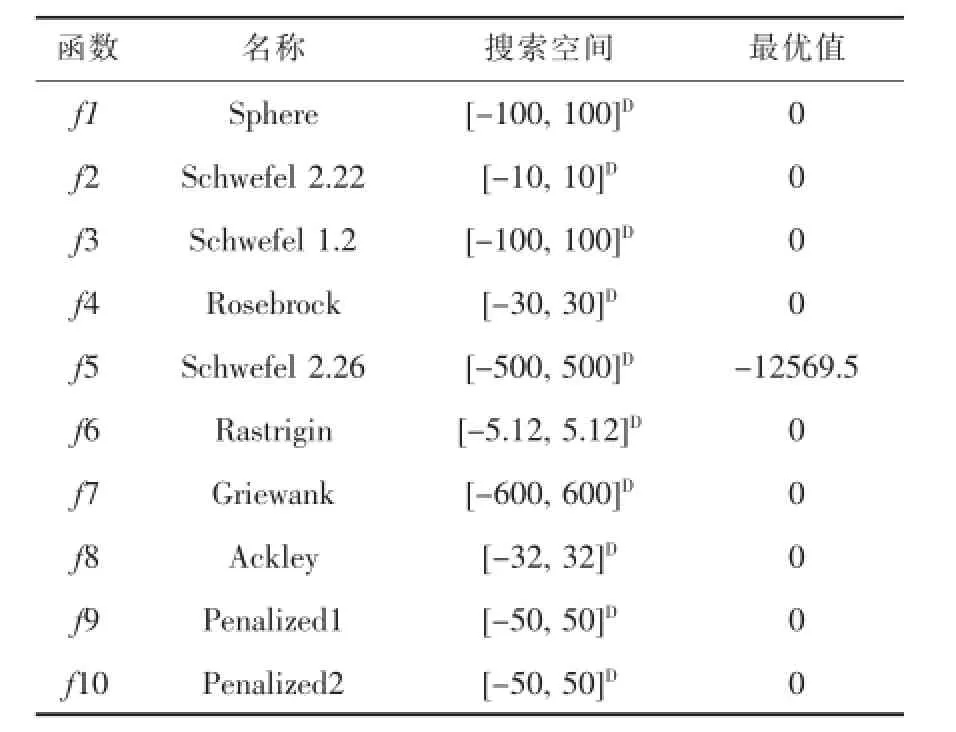
表1 Benchmark测试函数
在实验中,将CSFPA与FPA[1]进行性能比较,在CSFPA中设置了与文献[2]关于FPA算法相同的参数.此外,对上述两种算法的每次测试中,关于测试函数的结束条件设置上以400000作为评价次数,同时独立进行30次的实验验证,并把各算法所求解的实际最优值与理论最优值之间误差进行平均计算,将其结果和标准差作为评判算法优劣的指标.
3.2实验结果
FPA和CSFPA两种算法之间的对比实验结果图2所示,其中FPA的实验结果来自文献[11],并对实验结果按照文献[18]的方法进行统计分析,设显著性双尾t的水平值为0.05,其中在统计意义上,“+”代表CSFPA算法优于FPA,“-”表示FPA算法优于CSFPA算尖,“≈”表示两种算法无显著性差别.根据表2中的结果可以得出,在大部分测试函数上CSFPA算法比FPA算法更优.具体而言,CSFPA在4个单峰测试函数f1-f4上都获得了比FPA更优的解;在6个多峰测试函数上,CSFPA在测试函数上f5,f6,f7,f8,f10获得了比FPA更优的解.实验结果表明精英混沌局部搜索操作加快了算法的收敛速度,从而有限的计算开销下获得更优的解.


图2 FPA和CSFPA的收敛状态图

表2 实验结果
为了进一步比较FPA和CSFPA的收敛效率,图2给出了FPA和CSFPA在几个典型测试函数上的收敛曲线.从图2中可知,CSFPA比FPA具有更快的收敛速度,这是由于精英混沌局部搜索操作加快了算法的收敛速度.
4 结束语
FPA是一种新近提出的函数优化算法,它在求解许多复杂工程优化问题中获得了满足实际工程需求的优化结果,但许多研究人员发现基本FPA容易出现收敛速度慢的缺点,为了进一步提高基本FPA的收敛速度,本文提出应用精英混沌搜索的函数优化算法(CSFPA).在CSFPA的搜索过程中,随机选择出一个个体并对其执行精英混沌搜索操作增强算法的局部搜索能力,从而加快收敛速度.通过10个基准测试函数对CSFPA与基本FPA进行对比测试实验,结果表明CSFPA算法能够有效地改善FPA算法的收敛效率,同时CSFPA在大部分测试函数上解精度高于基本FPA的精度.
[1]Yang X S.Flower pollination algorithm for global optimization[M].Unconventional Computation and Natural Computation,Lecture Notes in Computer Science,2012:240-249.
[2]Yang X S,Karamanoglu M,He X.Flower pollination algorithm:a novel approach for multiobjective optimization[J].Engineering Optimization,2014,46(9):1222-1237.
[3]Wang R,Zhou Y.Flower Pollination Algorithm with Dimension by Dimension Improvement[J].Mathematical Problems in Engineering,2014:481791.
[4]Prathiba R,Moses M B,Sakthivel S.Flower pollination algorithm appliedfor different economicloaddispatchproblems[J]. International Journal of Engineering and Technology,2014,6(2): 1009-1016.
[5]Abdel-Raouf O,Abdel-Baset M,El-henawy I.A new hybrid flowerpollinationalgorithmforsolvingconstrainedglobal optimizationproblems[J].International Journal of Applied Operational Research,2014,4(2):1-13.
[6]Chakraborty D,Saha S,Dutta O.DE-FPA:A hybrid differential evolution-flower pollination algorithm for function minimization[C]//International Conference on High Performance Computing and Applications,Bhubaneswar,India,2014.
[7]Rodrigues D,Yang X S,de Souza A N,et al.Binary flower pollination algorithm and its application to feature selection[M]. Recent AdvancesinSwarmIntelligenceandEvolutionary Computation.Springer,2015:85-100.
[8]Dubey H M,Pandit M,Panigrahi B K.A biologically inspired modifiedflower pollinationalgorithmforsolvingeconomic dispatchproblems inmodernpower systems[J].Cognitive Computation,2015,7(5):594-608.
[9]肖辉辉,万常选,段艳明,等.基于模拟退火的花朵授粉优化算法[J].计算机应用,2015,35(4):1062-1066.
[10]肖辉辉,万常选,段艳明.一种基于复合形法的花朵授粉算法[J].小型微型计算机系统,2015,36(6):1373-1378.
[11]井福荣,郭肇禄,罗会兰.一种使用反向学习策略的改进花粉授粉算法[J].江西理工大学学报,2015,36(3):101-106.
[12]徐丈星,耿志强,朱群雄,等.基于SQP局部搜索的混沌粒子群优化算法[J].控制与决策,2012,27(4):557-561.
[13]龚安,吕倩,胡长军,等.基于混沌万有引力搜索算法的SVM参数优化及应用[J].计算机科学,2015,42(4):240-243.
[14]Jia D,Zheng G,Khan M K.An effective memetic differential evolution algorithm based on chaotic local search[J].Information Sciences,2011,181(15):3175-3187.
[15]田也壮.巴特莱法则二八定律与管理思想 [J].中国软科学,1995,7:80-81.
[16]郭肇禄,吴志健,汪靖,等.一种基于精英云变异的差分演化算法[J].武汉大学学报(理学版),2013,59(2):117-122.
[17]Yao X,Liu Y,Lin G.Evolutionary programmingmade faster[J]. IEEE Transactions on Evolutionary Computation,1999,3(2):82-102.
[18]Guo Z,Yue X,Zhang K,Deng C,Liu S.Enhanced social emotional optimisation algorithm with generalised oppositionbased learning[J].International Journal of Computing Science and Mathematics,2015,6(1):59-68.
An enhanced function optimization algorithm based on elite chaotic search
JING Furonga,GUO Zhaolub,LUO Huilana
(a.School of Information Engineering;b.Faculty of Science,JiangxiUniversity of Science and Technology,Ganzhou 341000,China)
Flower pollination algorithm(FPA)is an emerging function optimization algorithm.However,the traditional FPA tends to suffer from slow convergence when solving complex engineering optimization problems. Aiming at this weakness of the basic FPA,an enhanced flower pollination algorithm based on elite chaotic search(CSFPA)is proposed in this paper.In the evolution process,CSFPA randomly selects an individual to execute the elite chaotic search strategy,which can accelerate the convergence speed.In the experiments,the proposed CSFPA is compared with the basic FPA on several benchmark test problems.The experimental results validate the effectiveness of the proposed CSFPA.
optimization algorithm;evolutionary algorithm;chaotic search;flower pollination algorithm
TP181
A
2095-3046(2015)05-0074-06
10.13265/j.cnki.jxlgdxxb.2015.05.013
2015-09-10
江西省青年科学家(井冈之星)培养对象资助项目(20153BCB23010)
井福荣(1977-),男,讲师,主要从事智能计算、数据挖掘等方面的研究,E-mail:jephirus@126.com.

