应用微元模型探究平纹机织物延伸性问题

杨明霞，朱进忠，李 宁

(河南工程学院 纺织学院，河南 郑州450007)

机织物的耐用性特别是耐磨、耐洗性均比针织物好，但延伸性不如针织物，故如何改善机织物的延伸性及如何预测机织物的延伸性显得异常重要.

针对组织规律简单且应用广泛的平纹织物，分析查阅前人的研究结论［1-3］，借鉴Pierce理论与几何分析提出了假设，建立了微元理论模型，确定了建模所需要的参数，得到了数理关系，验证了这一关系的真实性.

1 织物微元模型的确立与分析

1.1 纱线应力伸长模型与分析

对纱线贴伏弧的存在及其拉伸过程中长度的变化做具体分析，以期准确得出经纱在模型单元中的长度与延伸后的形变.

借鉴Pierce理论模型，如图1所示.图1中，P为织物的平面轴线，模型中两个纬纱处于同一平面内，θ为经纱与织物轴线的夹角，也称为织造角，下文在处理分析时将θ直接表示为织造角，假定织物拉伸过程中经纬纱的直径不发生改变，则经纱段受力P0与织物轴P的垂直距离为r1+r2.

由于纱线的形变具有不可预测性，沿用纱线的理想弹性模型，假设织物中纬纱为刚性体、经纱为弹性体，经纱的受力模型见图2.

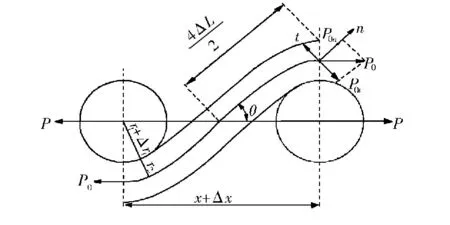
图1 Pierce理论模型Fig.1 Pierce theoreticalm odel

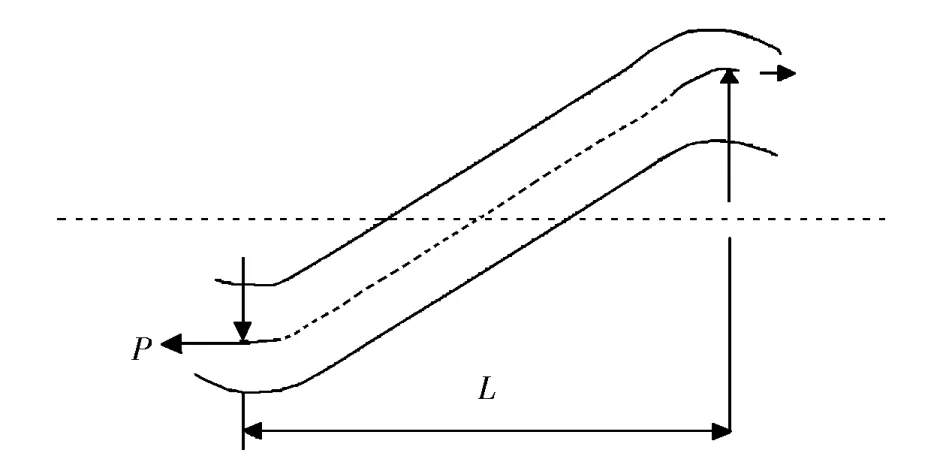
图2 经纱受力模型Fig.2 W arp forcemodel

如图2所示，在织物结构单元中，经纱段的受力可分为两部分，一部分是经纱的直线线段，另一部分是经纱两端与纬纱的贴附弧线段.假设受力过程中经纱为理想弹性体，故模型中弹性经纱段之内处处受力均匀.

为了验证假设的可行性，对于经纱是否在低负荷下符合受力与伸长的线性关系进行实验分析并讨论验证.在任何受力点经纱受力都为平行于织物轴受力的情况下，假定经纱长度为L、受力为P，则单位长度受力可以表示为

在后面的模型计算中，将对经纱进行分段受力分析，计算伸长量.

1.2 纱线微元组织中贴附弧理论分析

单元结构中贴附弧的变化模型如图3所示.假定单元模型中纬纱不发生位移，随着织物拉伸外力的作用，经纱会伸长变形，经纱与织物轴线的交点A，B也会相应移动至a，b，经纱将会移动至图示的虚线位置，经纱与纬纱的切点也相应地由O点移动至o点，也就是说经过拉伸形变，贴附弧缩短，贴附点向上发生转移，织造角变小，进而使经纱与织物轴线的交点发生位移，位移量便是所要探讨的结构变形量，单元结构的变形量直接影响着织物的受力延伸量.

分析得知，在贴附段经纱的两边及轴线都与纬纱边缘属于贴附关系，虽然在只分析经纱段时，经纱的两边及轴线段长度均不相同，但是在发生位移时，经纱与织物轴线3个交点的位移是不变的，所以两边与轴线的运算结果是一致的.下文将针对经纱段的中心轴线进行建模和几何分析.

图3 单元结构中贴附弧变化模型Fig.3 Changemodel of attached arc in cell structure

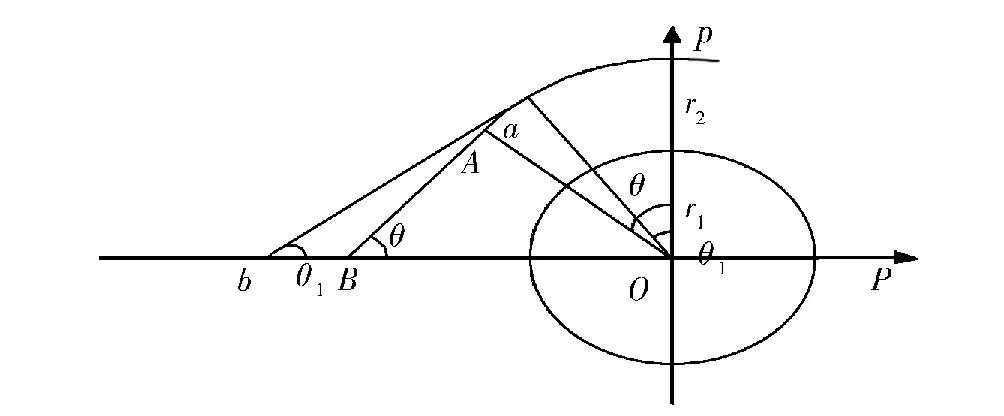
图4 经纱轴线结构模型Fig.4structuralmodel of warp axis

已知经纬纱线的特数，可以求出经纬纱的半径r1和r2:

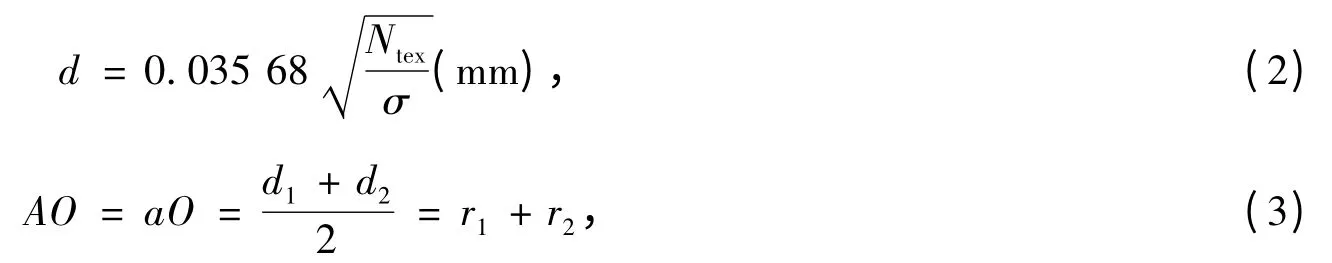
式中，Ntex为纬纱线密度，tex;σ为 经纬纱线标准状态下的体积质量系数.

已知织物的经纬向密度ρ经，ρ纬，可以求出单位宽度试样中单根经纱受力P和单元模型中经纱段受力p.

假设经纬密度的单位为根/cm，则试样中单根经纱的受力

进而，可得出单元模型中经纱段的受力

所以，模型中经纱段受力

式中，ρ经和ρ纬为织物的经纬向密度，根/cm;P0为对单位宽度单位长度测试试样加持的外力，cN.

还可得出结构模型中BO的长度，统一单位便可得到

求出BO后，根据模型中的集合关系便可得出织造角θ的大小，求导如下:

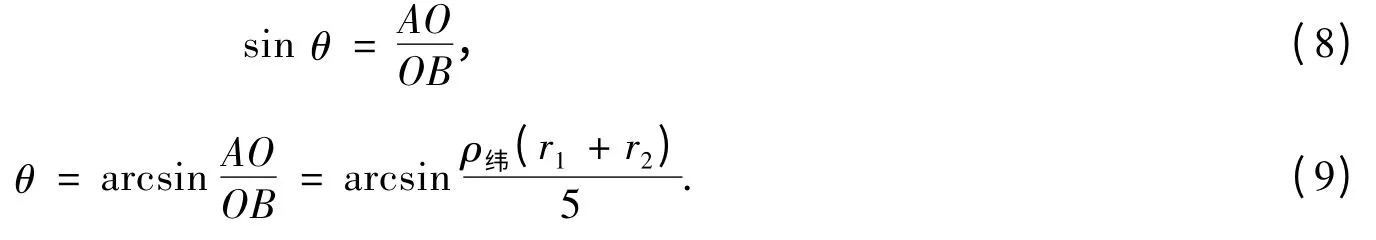
分析模型可知，受力变形前织造角应等于贴附弧所对应的角，都为θ，这样便可以把线段AB与贴伏弧pA的长度求出，进而求出模型中经纱段的长度，求导如下:

故经纱段总长

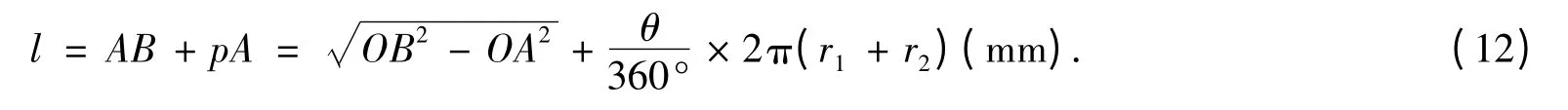
1.3 织物组织模型中经纱的受力分析

在分析经纱的受力伸长时，假设模型中纬纱是刚性的，经纱在低负荷下为理想弹性且经纬纱之间的滑动摩擦可忽略不计，在此基础上对经纱进行受力分析.因经纱为理想弹性状态，则经纱段内各点受力相同，见图5.

如图5所示，在经纱轴与织物轴交点处作受力分析，平行于织物轴的拉力p可以分解为垂直于经纱轴向的力p1和p2.垂直方向上分力的存在会使经纱与织物轴的交点向左发生位移，而沿经纱轴向的分力则可以使经纱伸长.垂直于经纱的分力会使经纱贴附点向上移动，这样的分力处理会使经纱免去摩擦力分析，也符合实际.关于水平总力的大小，把经纱看为内部受力均匀的，故总力与织物在一定宽度内拉伸力成正比，比值为纬向密度.

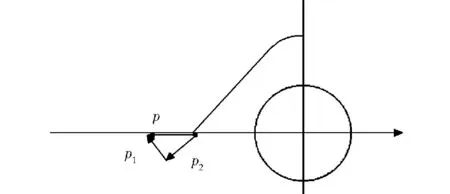
图5 经纱受力模型Fig.5 Warp force model

对图5进行几何分析:

在此，假设经纱的理想弹性系数为k，k代表经纱在单位长度内受单位外力时的伸长能力.由假设可知，经纱段内任意一点受力都为p2，则经纱段伸长

模型受力变形后的经纱长度

在受外力时，织造角变化为θ1，对形变后的模型进行几何分析:

联立如下:

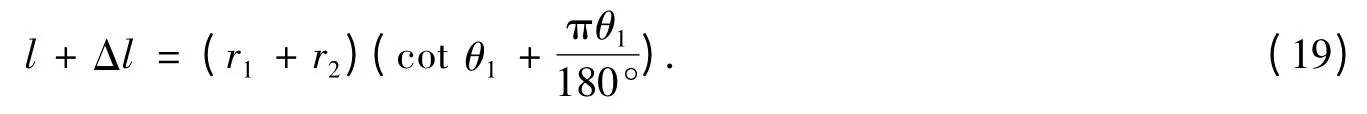
上式中可求出未知量θ1，运算后可求出形变前后的经纱轴长l和l'，以及织造角θ和θ1，由此可以得出单位结构中模型水平形变量，也就是经纱轴线与织物轴的交点位移Bb的长，计算如下:

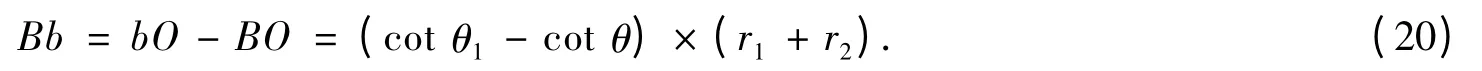
进而求得织物单位长度的伸长量

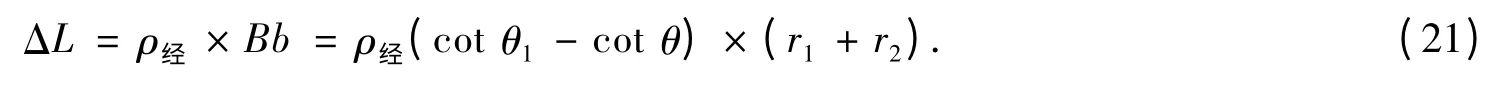
由上面的几何分析，可在假设建模成立的基础上求出织物单位长度在定负荷p作用下织物的伸长量

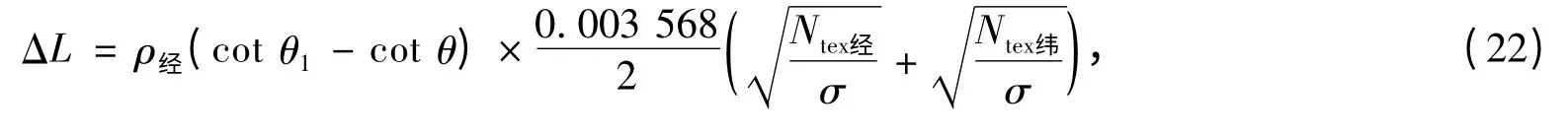
其中θ和θ1求导如下:

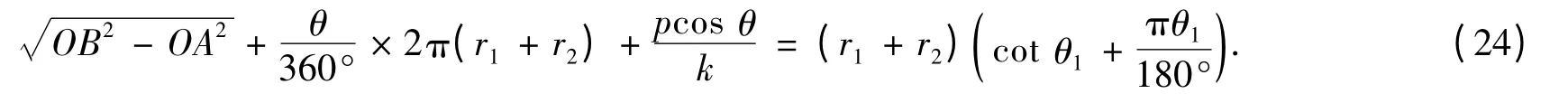
2 平纹组织结构模型的实验验证

针对上述模型所建立的数理关系测试织物的各个参数，处理实验数据并对上文提出的低负荷下经纱为理想弹性物体进行验证，进而对得出的参数因子与延伸性的数理关系进行论证.

实验所用材料有4种:试样1为低密高特平纹棉布;试样2为高密中特平纹棉布;试样3为中密涤棉混纺平纹布;试样4为高密高弹涤棉混纺布.

2.1 织物经纬密测试

为了单位的统一，将织物密度的单位换算为根/cm，织物经纬向密度测试结果见表1.

2.2 织物中纱线线密度和直径测试

织物中纱线线密度的测定参照纺织行业标准FZ/T 01093—2008［4］《机织物结构分析方法 织物中拆下纱线线密度的测定》，从没有除去非纤维物质的织物中拆下纱线，在实验用的标准大气中调湿后对其进行线密度的测试，结果见表2.进而由公式(2)计算出纱线的直径，结果见表3.

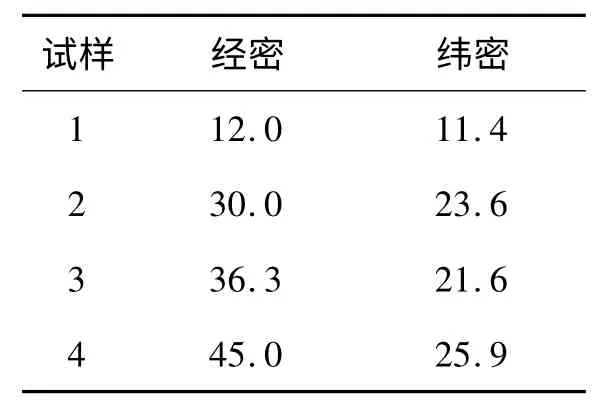
表1 织物密度测试结果Tab.1 Test results of fabric density根/cm

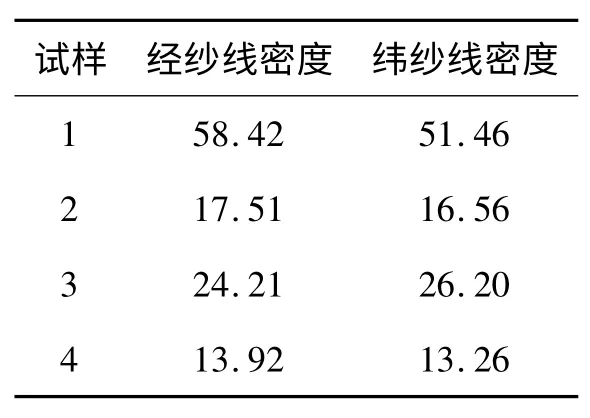
表2 织物中纱线线密度测试结果Tab.2 Test results of fabric yarn linear density in fabrictex

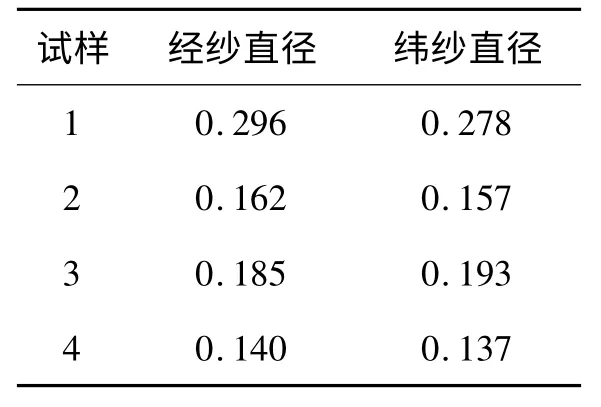
表3 织物中纱线直径的计算结果Tab.3 The results of fabric yarn diameters in fabricmm

2.3 织物中纱线弹性的测试

先对纱线进行拉伸断裂测试，然后在断裂应力的30%内设计梯度负荷对纱线进行定负荷弹性实验.用YG061型纱线弹性测试仪对织物中拆解的经纱进行定负荷拉伸，定力拉伸后停滞60 s待纱线不再伸长，以纱线的伸长量来分析纱线的弹性.

2.3.1 织物中经纱拉伸断裂性能测试

不同试样的断裂强力与断裂伸长测试结果见表4.

2.3.2 织物中经纱弹性负荷伸长测试

根据纱线断裂强力与断裂伸长的不同，在纱线断裂应力设置不同的梯度，测试不同试样在不同负荷梯度下的弹性，结果见表5.依照上述参数对试样中经纱进行弹性测试，试样的实测伸长数据见表6.

表4 织物中经纱的断裂强力与伸长Tab.4 Breaking strength and elongation of warp in fabric

表5 织物中经纱弹性测试的负荷Tab.5 Test gradient of warp elasticity in fabric cN

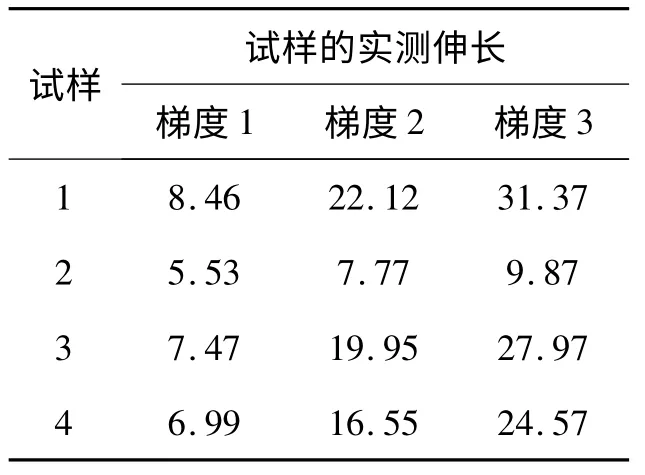
表6 织物中经纱的实测伸长数据Tab.6 Test results of warp elongation in fabric mm

对纱线在低负荷应力下的弹性系数进行计算:

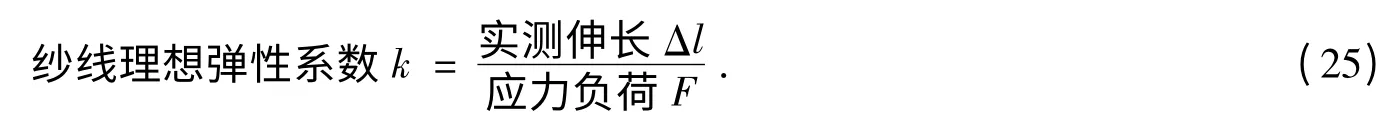
对表6中实测伸长进行理论分析可以看出，梯度1由于预加张力加持后纱线没有完全消除织缩或者纱线已经发生伸长等因素的存在，所以在计算中把梯度1当作一个基数进行处理，利用梯度2、梯度3与梯度1的差值计算出两个理想弹性系数，再对两个系数进行平均值计算，公式如下:

其中，F1，F2，F3分别是3个应力梯度的负荷值;Δl1，Δl2，Δl3分别是3个梯度的伸长量;k表征1 cN的力能使材料伸长k mm.

依照上述公式对4种试样进行计算，得出纱线的理想弹性系数，如表7所示.

表7 纱线理想弹性系数Tab.7 The value of yarn ideal elastic coefficients

2.4 织物低负荷应力下的延伸性测试

参照标准FZ/T 01114—2012《织物低应力拉伸性能的测试方法》［5］，用HD026电子织物强力仪对织物的断裂强力进行测试，根据其断裂强力设置织物的低负荷应力梯度，在低负荷应力梯度下对织物进行拉伸，拉伸速度设定为50 mm/min，拉伸停滞设为30 s，进而得到织物在低负荷应力下的延伸性.

织物断裂应力的测试结果见表8，低负荷应力梯度见表9，延伸性测试结果见表10.

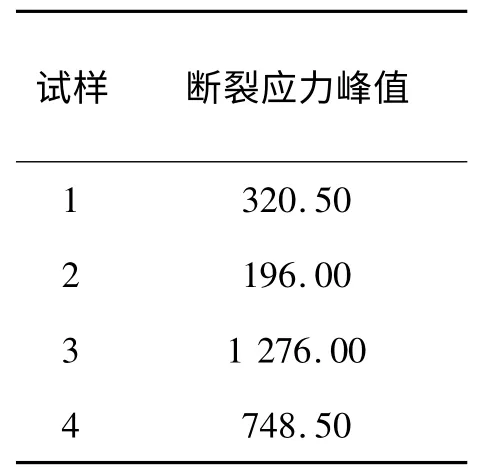
表8 织物断裂应力测试结果Tab.8 Test results of fabric fracture stress N

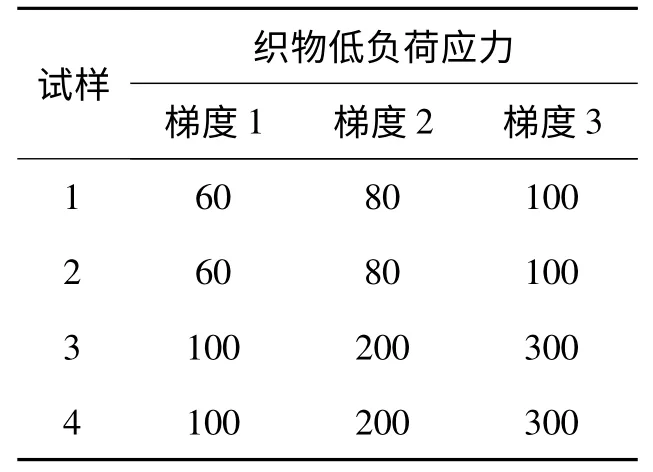
表9 织物低负荷应力梯度Tab.9 Low load stress gradient of fabric N

表10 织物的定负荷伸长Tab.10 Constant load elongation of fabric mm

2.5 织物应力伸长理论值与实验真值相关性分析

将依照上述实验所得的织物中纱线直径、经纬纱密度与织物中纱线低负荷下的弹性系数k，结合所建模型中的数理关系式(22)、(23)、(24)计算出织物应力伸长的理论值，结果见表11.

根据理论值与实验真值计算两者的相关系数，结果如表12所示.在表12中，相关度为理论值与实测值的比值，相关度越接近100%，表明两者的相关性越大.由表12可知:

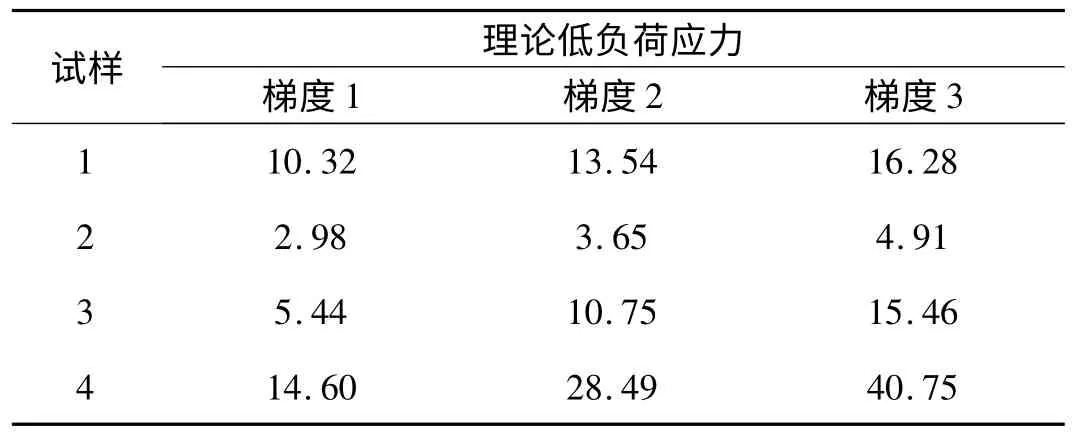
表11 织物低负荷应力的理论值Tab.11 Theoretical value of low load stress of fabric N

表12 织物模型应力伸长理论值相关性Tab.12 Theoretical value of stress elongation of fabric model

①对比同一试样不同应力梯度理论值与实测值的相关度可以看出，同一试样应力梯度中的应力负荷越小，所得相关度越高.因为随着应力的增加，假定的纱线应力伸长线性关系将发生改变.

②对比不同试样不同应力梯度的理论值与实测值的相关度可以看出，同为纯棉织物，试样1的相关度要小于试样2;同为涤棉混纺型织物，试样3的相关度就小于试样4.这是因为织物中纱线的弹性越好，模型所提出的纱线理想弹性理论越贴合实际，模型的适用性就越高.

③对比不同密度试样所得的相关度可以看出，经密越高的织物实验验证的相关性也越好.因为织物密度越高，其经纱在纬纱上的贴附弧长度也越长，模型也就越适用.

④总体来说，织物的实测值要大于模型预测的理论值.这是因为织物在拉伸过程中厚度发生了变化，纬纱直径与经纱直径减少引起织物的织造角θ变小，导致织物模型进一步横向伸长，故总伸长增加.

3 结语

根据上述模型与实验的相关性测试结果可得到所建模型的适用性，即所建模型更适用于应力负荷小、织物中纱线弹性好、织物密度高且厚度小的平纹组织织物.

［1］Pierce F T.The geometry of cloth structure［J］.Journal of the Textile Institute，1937，28(3):45-96.

［2］瞿畅，王君泽，高强.机织物几何模型及其计算机模拟［J］.纺织学报，2002，23(3):46-48.

［3］顾伯洪.机织物拉伸性能有限元模拟计算方法及应用［J］.纺织学报，1998，19(2):15-17.

［4］中华人民共和国国家发展和改革委员会.FZ/T 01093—2008机织物结构分析方法 织物中拆下纱线线密度的测定［S］.北京:中国标准出版社，2008.

［5］中华人民共和国工业和信息化部.FZ/T 01114—2012织物低应力拉伸性能的测试方法［S］.北京:中国标准出版社，2012.