梭形空间桁架的弹性临界荷载分析*
欧阳丹丹,付 波
(1.武警杭州士官学校,杭州310023;2.杭萧钢构股份有限公司,杭州310003;3.浙江大学 土木工程系,杭州310058)
梭形空间桁架是一种变截面桁架,结构由底面带斜杆的四角锥沿曲线方向排列组成,截面为倒三角形,桁架高度沿着跨度方向变化并在跨中达到最大值,其示意图如图1 所示。由于梭形桁架外形呈曲线状,简洁流畅,富于建筑表现力,因而备受建筑师青睐,近年来在大跨度建筑物的屋盖结构中得到较广泛应用。与等截面四角锥桁架相比,梭形桁架外形与梁弯矩图更为接近,故其承载效率更高,用料也更为经济。

图1 梭形空间桁架示意图
目前,在工程实践中,对梭形空间桁架的设计存在着以下两个主要问题:
(1)这类桁架一般仅在端部点支撑,其平面外失稳问题是设计中的主要矛盾,如何保证其整体稳定是工程设计人员所关心的问题之一。
(2)在桁架的稳定计算方面,现行空间网格结构技术规程(JGJ7)[1]仅规定了对立体桁架应设置平面外的稳定支撑体系,没有给出平面外失稳的临界荷载计算式,使得该类结构在应用时缺乏理论指导。
对第1 个问题,文献[2 -3]分别应用ANSYS和MIDAS 有限元分析软件对五个典型梭形桁架计算模型进行了线弹性稳定分析和非线性稳定分析,重点研究了考虑上弦系杆,上弦斜撑,屋盖檩条系统与桁架协同工作及端部支承形式对梭形桁架结构整体稳定的影响。计算结果表明增加上弦水平支撑,桁架端部采用双支座,考虑连续檩条协同工作均能有效提高梭形桁架结构的整体稳定性。
对第2 个问题,文献[4 -5]从理论上推导了四角锥系等截面空间桁架的等效抗弯刚度、抗扭刚度、抗剪刚度,并应用同时考虑弯、剪、扭刚度的势能驻值原理,导出了四角锥系等截面空间桁架的弹性临界荷载计算解析式。公式计算结果与有限元分析的结果相比吻合较好。但这两篇文献均未对梭形桁架的临界荷载进行分析。
本文在文献[5]的基础上,利用刚度等效原理将梭形桁架等效为等截面桁架,把变截面问题转化为等截面问题,从而将文献[5]导出的等截面空间桁架临界荷载计算式推广为梭形桁架的临界荷载计算式,并通过大量算例来验证公式的实用性。
1 等截面四角锥系空间桁架的临界荷载计算式
1.1 等截面四角锥单元的抗弯、抗扭、抗剪刚度
文献[5]以一个等截面四角锥单元(图2)为研究对象,通过该单元推导了四角锥系桁架的等效抗弯、抗扭、抗剪刚度,如式(1)~式(5)所示。四角锥单元各类杆件编号如图2 所示,公式中的Ai(i =1,2,…,9,10)为各杆的截面积,E、G 分别表示材料的弹性模量和剪切模量。

图2 四角锥单元

图3 四角锥截面
截面对x 轴的惯性矩为:

截面对y 轴的惯性矩为:

截面的扭转惯性矩:

式中:
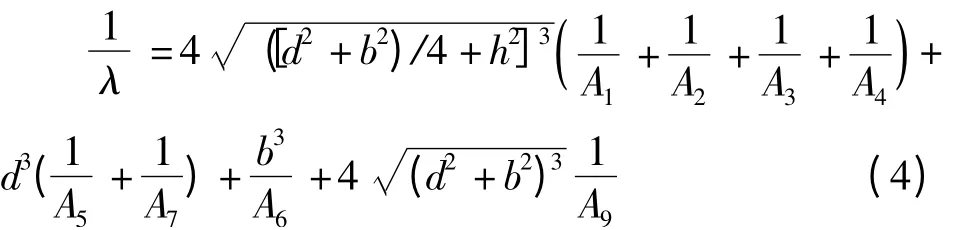
截面的抗剪刚度:

1.2 等截面桁架的临界荷载计算式
在得到了四角锥单元的各种刚度之后,文献[5]应用同时考虑弯曲-扭转-剪切变形的势能驻值原理,导出了等截面四角锥系桁架的临界弯矩表达式为:

式中:βy为不对称截面常数,a 为荷载作用点到截面剪心的距离,η 为考虑剪切变形的修正系数,这三个参数的表达式分别如式(7)~式(9)所示:


由式(6)可得到桁架的临界荷载为:

2 梭形桁架的等效抗弯、抗扭、抗剪刚度
从式(1)和式(3)可知,四角锥单元的抗扭刚度、x 向抗弯刚度均与桁架的高度有关,而梭形桁架(图1)的高度沿跨度方向是变化的,为克服数学上的困难,可将梭形桁架与具有相同跨度L 的等截面桁架进行刚度等效转换[6-7],将变截面问题转化为等截面问题,从而可利用等截面桁架的临界荷载计算式来计算梭形桁架的临界荷载。
2.1 抗弯刚度
四角锥截面的坐标系仍如图2 所示,梭形桁架的宽度沿着z 向没有发生改变,则截面对y 轴的等效惯性矩与式(2)相同:

截面对x 轴的惯性矩仍为式(1),但其中的四角锥高度h 是关于z 的函数:

对于梭形桁架,h(z)可用z 的二次函数进行拟合,令桁架跨中高度为h0,h(z)= b1z2+b2z +b3,由两端高度为0 和跨中高度为h0的条件,可得:

由上式解出b1= -4h0/L2,b2= 4h0/L,可得:

确定变截面桁架等效抗弯刚度的原则是按直接刚度计算的弯曲应变能Ub1与按等效刚度计算的弯曲应变能Ub2之差ε 最小。
建立ε 的表达式如下:

式中:
y1—等截面桁架绕x 轴弯曲时,y 向的挠曲函数;
y2—变截面桁架绕x 轴弯曲时,y 向的挠曲函数。
根据文献[6],对于两端简支的情况,可取y1m代入式(15),再利用使弯曲应变能之差ε 取极小值的条件= 0 (i = 1,2,,,,m)可求得I'x。


将式(14)代入上式经积分运算可得:



由式(19)的非零解条件可得:

展开行列式得到梭形桁架截面对x 轴的等效惯性矩:

2.2 抗扭刚度
由式(3)和式(4)所表征的梭形桁架截面的抗扭惯性矩是关于z 的函数:

式中:

确定变截面桁架等效抗扭刚度的原则是按直接刚度计算的扭转应变能Ut1与按等效刚度计算的扭转应变能Ut2之差ε 最小。
建立ε 的表达式:

式中:
φ1—等截面桁架绕z 轴扭转时的扭转角,其是z 的函数;
φ2—变截面桁架绕z 轴扭转时的扭转角,其是z 的函数。

若直接将λ(z)的表达式代入上式,第二项将难于进行积分。由于该项对抗扭刚度影响较小,可令λ(z)为常数以简化运算。由式(23)可看出当h(0.5L)= h0时,λ(z)取最小值。故可取λ(z)= λ(0.5L),这样得到的等效抗扭刚度要偏小一些。
在式(25)中令λ(z)= λ(0.5L),可得:

将h(z)代入上式经积分运算可得:

注意到It(0.5L)= 4λ(0.5L)Edb2,式(27)可改写为:


式(29)有非零解的条件为:

展开行列式可得到梭形桁架的等效抗扭惯性矩:

2.3 抗剪刚度
取出梭形桁架的一个四角锥单元进行分析,如图4 和图5 所示,θ 是上弦杆与z 轴之间的夹角。通常情况下,θ 在1°~8°Z 之间,cosθ ≈1 。故等效抗剪刚度可近似用式(5)来进行计算,此时式中的d = L/n,n 为梭形桁架的四角锥单元数。

图4 四角锥单元立体图

图5 四角锥单元立面图
通过上述推导和分析,得到了一系列梭形桁架的等效刚度,其中等效y 向抗弯刚度及等效抗剪刚度可沿用等截面桁架的表达式。
3 梭形桁架的临界荷载计算式
由式(7)和式(8)可知,荷载作用点到截面剪心的距离a 及不对称截面常数βy也与桁架高度有关:

设a'为等效的荷载作用点到截面剪心的距离,βy'为等效不对称截面常数。采用与上面相同的方法可列出由a(z)计算的外力势能与a'计算的外力势能之差ε1,以及由βy(z)计算的项与βy'计算的项之差ε2:

将梭形桁架的各等效刚度及参数代入式(6)替换掉相对应的项之后,可得到梭形桁架的临界弯矩计算式:

梭形桁架的临界荷载仍由式(10)来进行计算。
4 算例分析
选取22 榀典型梭形空间桁架作为算例,用式(35)、式(10)计算各榀桁架的临界荷载,桁架的几何尺寸见表1,配杆截面见表2,各计算模型中的杆件截面尺寸是利用空间网格结构设计软件MST2006 完成结构的静力分析后,按照满应力原则来进行设计的。
临界荷载的比较如表3 所示。表中的有限元解是利用有限元软件ANSYS 对同一桁架进行特征值屈曲分析的结果。从表中所列数据可知,本文就计算临界荷载的研究工作已覆盖跨度30 ~70 m 的梭形桁架范围,且计算结果与有限元数值分析结果基本一致,表明公式精度较好。

表1 桁架的几何尺寸表

表2 杆件截面尺寸表

表3 临界荷载比较
5 结论
(1)本文将梭形桁架与具有相同跨度的等截面桁架进行刚度等效转换,将变截面问题转化为等截面问题,利用等截面桁架的临界荷载计算式来计算梭形桁架的临界荷载。此时将梭形桁架的各等效刚度与参数Iy',It',βy',a' 替换掉等截面桁架临界荷载公式中的相应项即可得到梭形桁架的临界荷载计算式。
(2)从表3 可知,大量典型算例的结果与有限元解的误差均在±5%以内,说明将梭形桁架等效为等截面桁架,采用相同临界荷载计算式的做法具有一定的可靠性,计算结果可供工程设计参考。
[1]空间网格结构技术规程(JGJ7 -2010)[S]. 北京:中国建筑工业出版社,2010.
[2]丁圣果,付波,郑涛,等.梭形桁架式屋盖整体稳定的一阶屈曲分析[J]. 工业建筑:增刊,2010:417 -420.
[3]付波,丁圣果,郑涛,等.梭形桁架式屋盖整体稳定的非线性分析[J]. 工业建筑:增刊,2010:421 -422.
[4]付波,丁圣果,郑涛,等.四角锥系空间桁架的临界荷载[J].贵州大学学报:自然科学版,2009,26(5):101 -104.
[5]丁圣果,付波.大跨四角锥系空间桁架的临界荷载分析[J].四川建筑科学研究,2011,37(5):8 -11.
[6]吴亚平.变截面压杆稳定性计算的等效刚度法[J]. 力学与实践,1994,16(1):58 -60.
[7]吴亚平.对变截面压杆稳定性计算的等效刚度法的改进[J].兰州铁道学院学报,1998,17(4):4 -6.

