基于SPSS的客车产品研发失效因子分析

刘运强，张文凤，吕勇

（桂林航天工业学院机械工程系，广西桂林541004）

基于SPSS的客车产品研发失效因子分析

刘运强，张文凤，吕勇

（桂林航天工业学院机械工程系，广西桂林541004）

利用影响客车研发失效的14个调查测量数据，运用因子分析法，使用SPSS软件分析影响客车产品研发失效的主要原因。分析结果表明，引起失效的主要原因是：产品研发综合管理水平、研发中心技术水平、研发人力资源管理。

SPSS；客车产品；研发失效；统计分析

SPSS（Statistical Productand Service Solutions）即IBM公司“统计产品与服务解决方案”软件，是全球专业统计分析软件的领导者，一直致力于帮助企业提升科学运用统计分析方法的能力。它包含了丰富的统计分析算法，与SAS、SATA相比，SPSS不需要编程，只要求掌握基本的统计原理［1-2］。SPSS软件在国外已广泛地应用于电信、医疗、银行、证券、保险、制造、商业、科研、教育等行业，从数据中总结、归纳有用的知识，并将知识用于市场营销、运营决策和信用风险管理等方面，帮助企业降低消费、增加效益，从而提高整体运行效率［3］。

目前，大多客车企业每年逐渐增加研发费用，研发队伍也大多维持在50～100人，但面对外部竞争，新产品仍缺乏竞争力。影响客车产品研发成功率的因素很多，本文以某客车企业研发失效为例，通过SPSS因子分析，分析影响该企业产品研发失效的主要因子，以期对产品开发的综合管理提供科学依据。

1　 SPSS研究方法

1.1资料收集及统计分析方法

采用问卷调查的方式，对企业管理、设计、工艺、质量、销售、用户等人员进行调查。问卷共设计缺乏产品战略及规划、产品没有明确的市场定位、领导直接干预项目，或项目缺乏控制、协调和沟通困难等14个测量项目，采用5级评分制，即根据各因素对产品研发失效的影响力大小划分为5个等级，分别为1=“毫无影响”，2=“影响较小”，3=“有一定影响”，4=“影响较大”，5=“影响很大”。

分析调查数据常用的方法主要有描述性统计分析、稳态状态分析、回归分析、因子分析、主成分分析以及现代优化算法分析等，它们各自都有优缺点。本文采用SPSS分析软件对整理后的调研数据进行统计描述和分析。SPSS软件具有操作简单、分析的结果直观清晰、可直接读取DBF和EXCEL文件、能兼容各种操作系统的优点，现已得到广泛的应用。1.2描述性统计分析的原理

对回收的有效问卷进行整理，并录入SPSS系统，其中X1-X14分别代表问卷中的14个问项。SPSS采用的描述性统计分析方法，主要对样本中所有观测的平均值（即均值）和标准差进行分析，用于描述样本的中心位置。

对于样本为X1，X2，…，Xn的观测数据，其均值X和方差σ2的计算公式分别为

标准差能反映一个数据集的离散程度，平均数相同的，标准差未必相同。标准差值小可以说明各观测样本与均值较为接近，数据的离散程度小；标准差值大可以说明数据中各观测样本和均值的差异较大，数据的离散程度大。

标准差σ的计算公式为

2　 SPSS结果分析

本文先从数据可靠性方面对采集的数据进行信度分析，检测数据的可靠性和稳定性，然后进行均值、方差分析，因子分析及公因子方差分析，最后进行旋转矩阵分析。

2.1信度分析

信度（Reliability）即可靠性，指标主要有等值系数、内在一致性系数和稳定系数。通过对数据的信度分析，以确保其可靠性和稳定性，以免影响问卷内容分析结果的准确性。信度分析主要有α信度系数法、复本信度法、折半信度法和重测信度法四种方法。本分析采用目前常用克朗巴哈（Cronbach）α信度系数法以及KMO（Kaiser-Meyer-Olkin）检验、Bartlett检验。SPSS分析结果如表1所示。

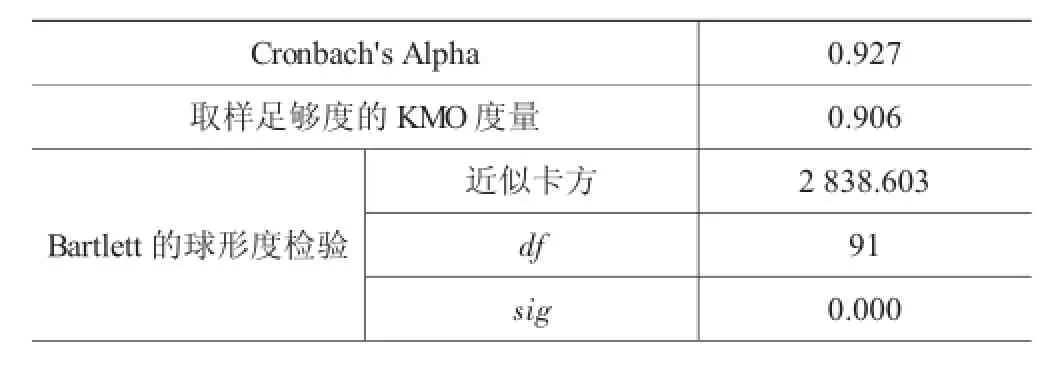
表1　 KMO和Bartlett的检验

其中克朗巴哈α信度系数的计算公式如下：

式中：K为测量项目的总数，即调查问卷有效回收数量137份；是全部测量项目总和的方差，本文为

100.21；i是测量项目数量14；n等于调查问卷有效回收数量137份；Yi为第i项测量项目的得分的方差，由公式（2）计算。Cronbachα系数经计算为0.927，信度较高，可以进行因子分析。

KMO检验统计量是用来比较变量间简单相关系数和偏相关系数的大小，主要用来检验数据是否适合因子分析的［4］。计算原理是所有原相关系数的平方和除以简单相关系数平方和加偏相关系数平方和。根据文献［2］，KMO的数值变化从0～1，如果原变量间相互作用较大，变量间的偏相关系数就会相对较小，简单相关系数则相对较大；Kaiser提出的判断标准：KMO＞0.9时非常适合做因子分析；0.8＜KMO＜0.9为适合；0.7＜KMO＜0.8为一般；0.6＜KMO＜0.7为适合并较低；KMO＜0.6为适合度较低。本案例根据文献［5］中的计算公式得到KMO的值为0.906，表示该样本可以做因子分析［6］。

Bartlett检验是方差齐性检验的一种。如果Bartlett的球形度检验的统计量数值较小，则认为相关系数矩阵可能是一个单位矩阵，不适合做因子分析；如果统计量数值较大，即原变量间的相关性显著，则适合于做因子分析。本例中经计算近似卡方（Approx.Chi-Squarie）= 2 838.603，近似卡方的计算公式是实际观察次数与理论次数（又称期望次数）之差的平方再除以理论次数所得的统计量。df为自由度，一般指样本中可以自由变动的变量的个数，但卡方分析自由度是依据样本的类别，也就是说，在137个样本中被分成了92个类别，即df=91。sig为差异显著性指标，指系统计算出的相应显著性统计量出现的概率，一般大于0.05表示差异不显著，小于0.05表示差异显著，小于0.01表示差异极显著。本例经计算sig=0.00。在本例中，自由度df和sig值显著，表示数据正态分布，适合做因子分析。

2.2均值及标准差分析

SPSS软件生成“描述统计量表”（见表2）。该表包含极大值、均值、标准差和方差四个系列数值。经分析，14个因素的均值均落在2.46～4.31之间，说明这些因素均对产品研发失效有一定影响。其中，缺乏产品战略及规划、产品没有明确的市场定位、领导直接干预项目，或项目缺乏控制、协调和沟通困难、项目管理无效、项目计划或任务得不到及时完成等项目的均值在4.0以上，影响程度较大。而标准差较小的前4个项目，说明对这几项的评价意见相差不大，结果比较接近于平均值，反应这些项目是影响产品失效的主要因素。为了进一步对失效原因进行定量分析，使用因子分析方法。

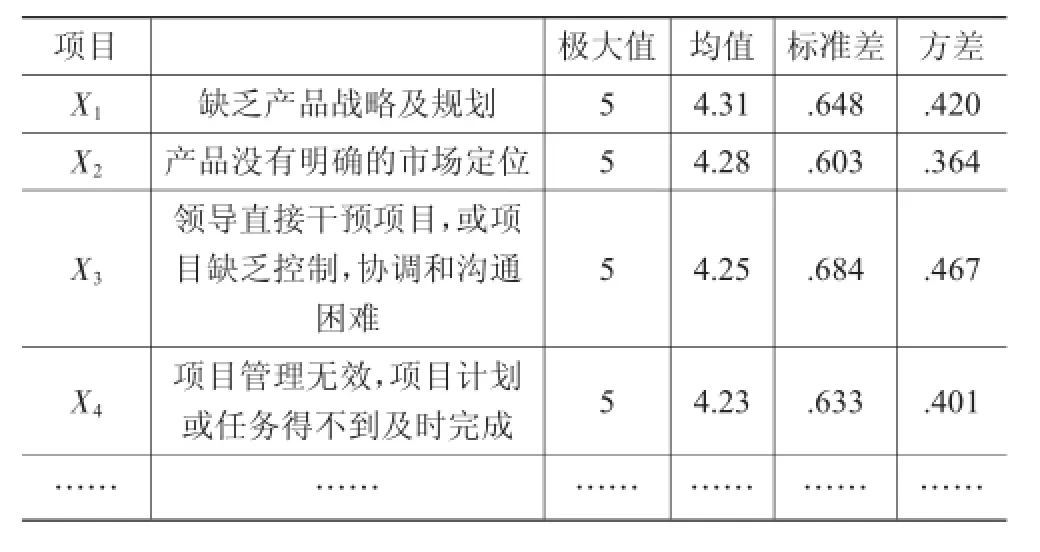
表2　描述统计量表

3　影响客车研发失效的因子分析

3.1因子分析的统计思想

大量观测的数据分析起来十分困难，必定存在某些高度相关的，把这些相关的变量组成一组，在同一组内变量彼此具有高度相关性，而与其他各组的变量却只有较少的相关或不相关，把这种同一组内高度相关的变量称为公共因子。这样就把较多的观测变量变为几个公共相关的变量。其分析过程是通过对原始变量的相关系数矩阵内部结构的研究，求出少数几个综合变量，再用综合变量描述原始的变量之间的关系，导出描述变量间本质联系、变量与公共因子的关系的负荷矩阵。再根据负荷矩阵，按变量与公共因子相关性重要程度分组，使同组内的变量之间的相关性较高，不同组的变量的相关性较低，按公因子包含变量的特点即公因子内涵对因子作出解释与命名［7］。这样，就把多个变量归解到少数的几个公因子，更便于查找引起冲突的原因。

3.2因子分析数学模型

假定有n个样本，每个样本共有p个变量，构成一个n×p阶的数据矩阵：

因子分析用少数几个假想变量来表示其基本的数据结构。当p较大时，在p维空间中分析问题很麻烦。为了降低难度需要进行降维处理，即用几个有代表性的综合指标代替原来指标，并且使这些指标既能尽量多地反映原来指标所反映的信息，同时它们之间又是彼此独立的。

设有n个样本，p个指标，X=（X1，X2，…，XP）T为随机向量，公因子为F=（F1，F2…Fm）T，则因子模型如下［8］：

式中：A=（aij）是因子载荷矩阵；aij是公因子Fj与测量项目Xi的相关系数，即因子荷载；εi代表公因子以外的影响因素，为特殊因子，在实际分析时可以忽略。

求出公因子Fj后，用回归统计等方法建立公因子权重系数数学模型，用公因子建立线性方程，计算出公因子权重系数bji，对各种模型进行综合评估［9］。

3.3测量项目的共同度

通过因子分析方法，在保持测量项目相互关系原则下，寻找变量的公共因子，如公式（7），建立用较少的因子表示原来的变量的关系式，如公式（6），以弄清问题影响的关键因素。在用有本质意义的少量公因子来归纳原来测量项目前，先用主成分分析方法，分析测量项目的共同度。主成分分析是通过少数几个主要分量来解释多个变量间的内部结构，在样本数据信息损失最小的原则下，对高维变量进行降维，用较少的变量表示原来的样本，一般通过求相关矩阵的特征值和相应的特征向量，取前几个计算主成分。

测量项目的变量的共同度即公因子方差比，是表示各变量中所含原始信息能被提取的公因子所表示的程度，通过主成分分析法提取公因子方差，如表3所示。从表中可知，在变量的初始共同度均为1，在被指定条件下提取特征根时，70%的变量共同度都在80%以上。因此，提取出的这几个公因子对各变量的解释能力是较强的，这些变量的信息丢失程度较少［2］。

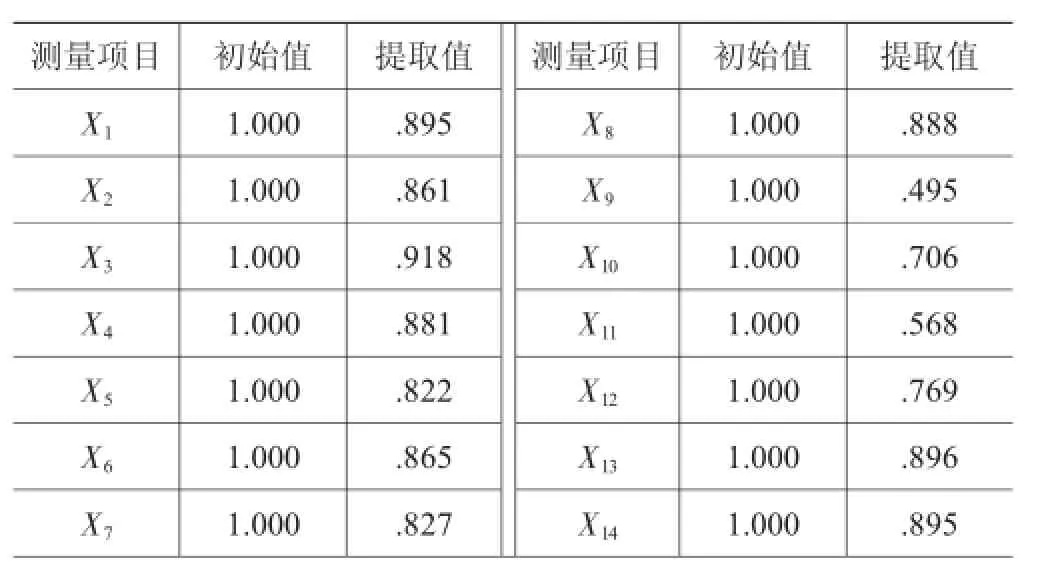
表3　公因子方差比

3.4方差累计贡献率

公因子Fj的方差贡献率是在因子载荷矩阵A中，各列元素aj的平方和，它是衡量公因子相对重要性的指标。方差贡献率越大，表明公因子对X的贡献越大［2］。

表4为解释总方差和累计贡献率，表中的“成分”是SPSS软件中的名称，这里可以理解为公因子；“初始项特征根”中的“合计”是主成分（即主要因子）影响力度的指标，代表引入该公因子后可以解释平均多少测量项目的信息，如果特征值小于1，说明该主成分的解释力度还不如直接引入一个原测量项目的平均解释力度大。因此，一般用特征值大于1作为计算标准；“初始特征根”中的“方差贡献率”，表明第i项的公因子在全部方差中的比重，这个值越大，表明第i项公因子综合测量项目的信息能力越强。“初始特征根”中的“累计贡献率”指至第i项的公因子累计提取了测量项目多少信息，一般建议累计贡献率达到80%左右，就可以表明前i个公因子基本包含了全部测量指标的信息，前i项公因子就可以被提取。

表4中只有前3个成分的特征根值大于1，提取前3个公因子可以反映原有变量80.617%的情况，信息丢失相对较少，所以本例只提取前3个公因子。3.5旋转成分矩阵分析

表4　解释总方差和累计贡献率

表4中前3个公因子能较好反映14个测量项目，但各因子的意义不是很明显，不利于因子解释。为了使因子载荷矩阵中的系数更加明显，对初始因子载荷矩阵进行因子轴的旋转，使因子和原始变量间的关系进行重构，使得因子载荷矩阵中各元素数值在0～1范围内，同时保持同一行中各元素平方和（公因子方差）不变。通过因子旋转，各测量项目在因子载荷上更加明显，有利于对各公共因子给出明确的解释。采用方差最大法对因子载荷矩阵实施正交旋转，旋转后的因子载荷矩阵见表5（表5的名称使用SPSS报表的名称）。

根据公式（6），本文研究的14个测量项目可以用3个公因子F1、F2、F3来描述，因子载荷矩阵见表5。比如：

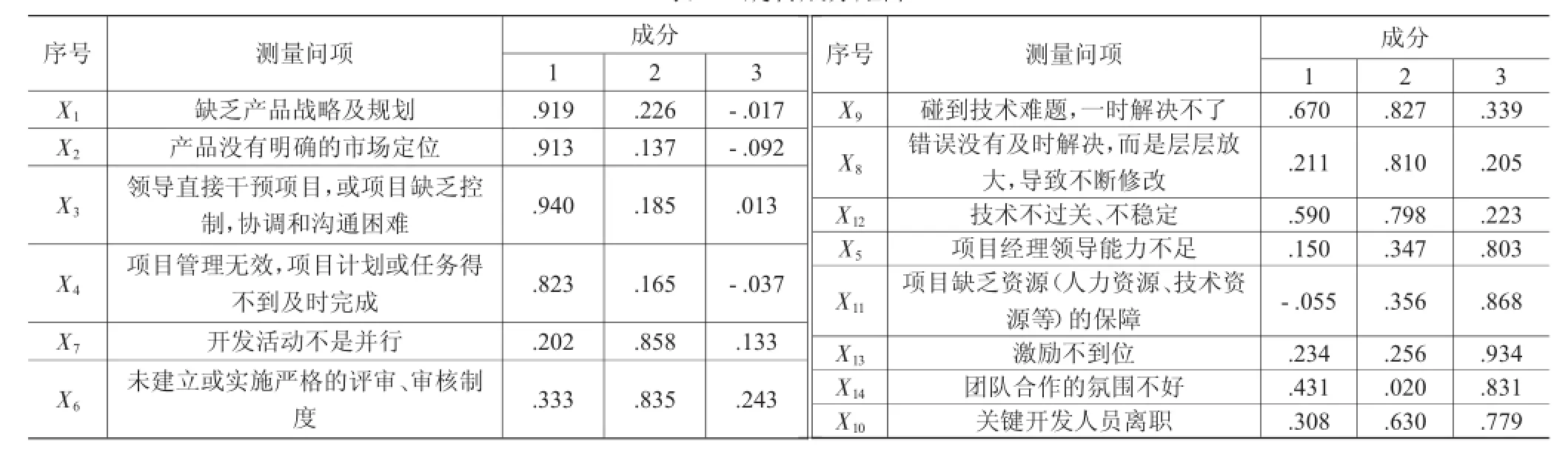
表5　旋转成分矩阵

公共因子F1、F2、F3是不可观测的潜在因子，上式中可以忽略εi，即F1、F2、F3反映影响产品研发失效因素的3个潜在的影响因子。为了便于对F1、F2、F3进行解释，根据公式（7），从表5可得3个公因子F1、F2、F3的构成。以公因子F1为例：

从公式（11）和表5中可以看出，公因子F1（第1主成分）中，X1、X2、X3、X4的公因子权重系数分别为0.919、0.913、0.940、0.823，这4个公因子权重系数明显比其他的要大很多，即F1主要反映测量项目X1-X4的综合问题，X1-X4分别为缺乏产品战略及规划、没有明确的市场定位、领导直接干预项目，或项目缺乏控制，协调和沟通困难、项目管理无效，项目计划或任务得不到及时完成的负荷较大等。因此，公因子F1反应的是产品研发综合管理水平（产品规划、产品定位、产品开发管理）；公因子F2综合反映X7-X12测量项目，即开发活动不是并行，未建立或实施严格的评审、审核制度，碰到技术难题一时解决不了，错误没有及时解决，而是层层放大，导致不断修改、技术不过关、不稳定的负荷较大。因此，F2主要反映研发中心技术水平。同理，可解释公因子F3主要反映了研发人力资源问题。

4　结束语

通过问卷抽样调查、专家交流，对14个统计量进行采样，运用SPSS软件进行因子分析。分析结果表明，该企业研发失效的主要原因是产品研发综合管理水平、研发中心技术水平、研发人力资源管理三个方面的问题。不同的企业，产品研发失败的原因也不同，客车企业为了避免产品研发失效，应根据自身的情况制定产品中、长期开发规划，提高产品开发综合管理水平，加强技术储备和人才培养，建立健全项目管理与团队建设以及有效的评价与激励机制，缩短产品开发周期，提高新产品研发质量、产品研发成功率，持续提高企业新产品的市场竞争力［10］。

［1］白中浩，马伟杰，曹立波，等.乘用车-货车追尾碰撞事故分析及其试验与仿真研究［J］.中国机械工程，2010，21（14）：1742 -1747.

［2］GB 11567.2-2011，汽车和挂车后下部防护要求［S］.北京：中国标准出版社，2011.

［3］马讯，郝琪，周宗良.汽车后防护装置的碰撞仿真分析［J］.公路交通科技，2009，26（4）：133-137.

参考文献：

［1］吴占福，马旭平，李亚奎.统计分析软件SPSS介绍［J］.河北北方学院学报，2006，（6）：67-69.

［2］张文彤.SPSS统计分析高级教程［M］.北京：高等教育出版社，2007.3.

［3］丁雪梅，徐向红，邢沈阳，等.SPSS数据分析及Excel作图在毕业论文中的应用［J］.实验室研究与探索，2012，（3）：122-128.

［4］孙晓松，朱鹏程.借助SPSS软件的成绩因子分析［J］.通化师范学院学报：自然科学版，2013，（6）：13-16.

［5］董毅.因子分析在水系沉积物测量地球化学分区中的应用探讨—以青海都兰地区为例［J］.矿产与地质，2008，（1）：78-82.

［6］田金亭，朱强忠，张凤霞，等.方差分析法在产品检验中的应用［J］.聊城大学学报：自然科学版，2008，（1）：23-24.

［7］梁斌，卓梅霞.基于SPSS统计软件的因子分析法及实证分析［J］.河西学院学报，2011，（5）：45-49.

［8］何亮.主成分分析在SPSS中的应用［J］.山西农业大学学报：社会科学版，2007，（S1）：20-22.

［9］李小胜，陈珍珍.如何正确应用SPSS软件做主成分分析［J］.统计研究，2010，（8）：105-108.

［10］罗伯特·G·库珀（Cooper.R.G）.新产品开发流程管理［M］.北京：电子工业出版社，2010.1.

修改稿日期：2015-01-13

Analysis on Failure Factors of Bus / Coach Products Research Design Based on SPSS

Liu Yunqiang，ZhangWenfeng，LüYong
（DepartmentofMechanical Engineering，Guilin University ofAerospace Technology，Guilin 541004，China）

The authors analyze the failure reasons for the bus / coach products research design usingthe factors analysismethod and SPSSsoftware byutilizing14 surveyingmeasurement datawhich affect the failure ofbus / coach products research design. The analysis results showthat the main reasons are products development comprehensive management level， technologyand development level ofresearch center and themanagement ofresearch center human resource.

SPSS； bus / coach product； failure of research design； statistical analysis

U469.1

A

1006-3331（2015）05-0029-05

刘运强（1971-），男，硕士；高级工程师；研究方向：材料成型与控制。