基于经济流速先验信息的启发式管网优化设计

丁　琨， 张　甲， 张　明， 金菊良， 张　勇

(1.安徽建筑大学 环境与能源工程学院，安徽 合肥 230601；2.安徽工程大学 建筑工程学院，安徽 芜湖 241000；3.合肥工业大学 土木与水利工程学院，安徽 合肥 230009)

基于经济流速先验信息的启发式管网优化设计

丁琨1， 张甲1， 张明2， 金菊良3， 张勇1

(1.安徽建筑大学 环境与能源工程学院，安徽 合肥 230601；2.安徽工程大学 建筑工程学院，安徽 芜湖 241000；3.合肥工业大学 土木与水利工程学院，安徽 合肥 230009)

针对传统遗传算法在管网设计中存在计算结果误差较大、寻优效率较低等问题，采用经济流速约束、流量约束和罚函数等改进措施，提出了基于经济流速先验信息的启发式优化方法.通过一个实例验证了该方法可以提高遗传算法的收敛速度和寻优效率，计算结果较准确，且管网设计合理，可降低工程投资.

给水管网；优化设计；经济流速；经济管径；罚函数；遗传算法

给水管网是供水系统的重要组成部分，承担着输送生产、生活和消防用水的任务，是市政建设关键基础设施之一.随着城镇化建设速度的加快，要求不断提高给水管网建设水平，因此，科学布局给水管网系统，降低运行维护费用和供水成本，保障供水安全是当务之急.通常在给水工程总投资中，给水管渠和管网占整个供水工程投资的70%～80%，在工程投资有限的条件下，进行给水管网系统的优化设计，对提高给水系统的经济效益、社会效益和环境效益具有重要意义[1].管网设计通常直接引用经济流速或采用传统遗传算法优化，但计算结果误差较大、寻优效率较低.本文引入经济流速约束、流量约束和罚函数等改进措施，加快遗传算法收敛速度，提高寻优效率，可使计算结果较精确，且管网设计合理，从而降低工程投资.

1　管网设计的遗传算法模型

1.1遗传算法概述

遗传算法[2-3](genetic algorithms，GA)是由美国Michigan大学的John Holland教授于1975年创建的.他受进化论、群体遗传学说和物种选择学说的启发，创立了一套模拟自然界中遗传机制和生物进化论的过程搜索最优解的算法，其显著特点是基本上不需要所求问题的信息，只需目标函数，而且也不受搜索空间是否连续或可微的限制，就可以求出全局最优解.遗传算法适用于解决复杂的非线性和多维空间寻优问题，在自动控制、模式识别、科学计算、工程设计等方面被广泛应用.

1.2遗传算法运行步骤

(1) 算法随机生成一个初始的、随机的种群.

(2) 算法使用当前种群的个体生成下一代的种群.为了生成新的种群，算法将会执行下列步骤：

① 通过计算适应度值给每个群体中的个体打分；

② 标定原始的适应度值到一定的数据范围之内；

③ 依据适应度值选择群体中的成员，称为父代；

④ 在当前群体中一部分个体有更高的适应度值，这一部分被称为“精英”，这些精英们被直接复制到下一代中；

⑤ 从父代中产生子代个体，使用“交叉”的方法产生下一代，再使用“变异”的方法对下一代个体中的基因产生小几率的改变，从而产生新的个体；

⑥ 使用产生的子代个体替换当前群体中的个体，进而产生下一代群体.

(3) 当算法满足停止标准中的设定值时，算法停止.

1.3目标函数的数学模型

管网技术经济计算是以管网造价和运行管理费用为目标函数，并将其余相关性的要求作为约束条件，建立用于优化计算的约束条件和目标函数的数学表达式，求出一定年限内供水管网建设费用与管理费用之和为最小时的管径或水损，即求出经济管径或经济水损.管网的建设费用主要包括管线的建设费用，管理费用主要包括供水所需的动力费用.由于管网的技术管理和检修等费用所占比例不大，在模型中给予忽略.管网定线工作完成后，管段的长度基本确定，因此，管网的建设费用和管理费用仅取决于管段中的流量或管径[1].管网优化计算目标函数的数学模型[4]如式(1)所示.

(1)

式中：W为管网的年折算费用(元)；p为管网每年折旧和大修的百分率(%)；t为投资偿还期(a)；E为电费(元/(kW·h))；Q为水泵流量(m3/s)；H0为水泵静扬程(kPa)；η为泵站的效率(一般为0.55～0.85)；di，li分别为管段i的直径和长度(m)；ρ为水的密度(1 t/m3)；g为重力加速度(9.81m/s2)；δ，a，b为单位长度管网造价[1,5]公式中的指数和系数，依据当地管材和施工条件而定；β为能量变化系数.

约束条件：

(1) 水力平衡条件.各节点的流量平衡，即 qi+∑qij=0，qi为节点i的节点流量(L/s)；qij为从节点i到节点j的管段流量(L/s)；各环闭合差为零，即∑(hij)k=0 ，(hij)k为第k环中的第i至第j节点管段水头损失，k为管段编号.

(2) 节点水压约束.各节点的水压应该在最大水压和最小水压之间，即Hmax≥Hi≥Hmin，Hi表示第i节点的水压.

(3) 管径约束.管径约束包括最小管径约束和标准管径约束，即所有管径的最小值应该等于最小管径，其他类型的管径应该为标准管径中的某一种.

1.4改进后的目标函数的数学模型

在目标函数的数学模型中加入了流速约束和流量约束，其中,流速约束是以经济流速为参考值，流量约束是以每种规格的经济管径的中间流量作为参考值.同时，采用罚函数对闭合差不满足要求的管径组合和流速流量不合理的管径组合进行直接淘汰，提高算法的收敛速度.改进后的目标函数的数学模型如式(2)所示.

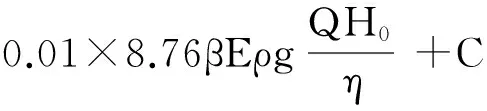
(2)

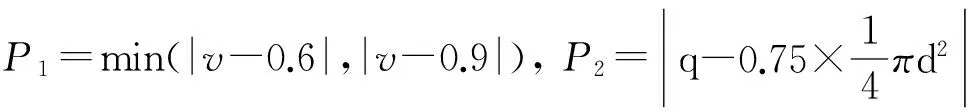
2　管网平差计算

2.1水头损失计算

水头损失计算采用舍维列夫公式[1，6]，其适用于旧铸铁管和旧钢管，当水温10 ℃时

I=αqij2=0.00107v2/D1.3v≥1.2m/s

(3)

I=αqij2=0.000912v2/D1.3(1+0.867/v)0.3

v<1.2m/s

(4)

式中：I为水力坡度；α为管段比阻；v为水流速度(m/s)；D为管段的计算内径(m).

计算管段水力坡度时，当v≥1.2 m/s，舍维列夫公式的比阻α=0.001736/D5.3；当水流在过渡区v<1.2m/s时，为保证计算的准确性，对式(4)计算的比阻乘以修正系数K，且K=0.8529×(1+0.867/v)0.3.

2.2初分流量

由于城市商业银行的特殊性，自身的风险管理能力和盈利能力相较股份制银行均较差。区块链技术增加了金融风险的传染性和隐蔽性，其在银行的实质性应用将使传统的技术风险、信用风险、法律风险、操作风险披上科技的外衣，导致城市商业银行风险防控再一次重塑。

本文的管网流量由计算机根据管径和管长的大小按比例进行自动分配.设第i个节点的节点流量为qi，设其上游有m根管段与其相连，下游有n根管段与其相连，每根管段的计算内径为Di，每根管道的流量为Qi.由于每根管道的管径已经随机生成，故每根管道的比阻也是已知的，令为αi.

从节点i上游过来的流量为，每根管道的比阻αi=0.001736/Di5.3，每根管段的计算流量的份额，则下游每根管段的分配流量为.根据此方法能够实现计算机自动分配流量，无需人工手动输入，为程序的自动运行提供了基础.同时，该流量分配方法运用比阻，在考虑管径的同时，还考虑管长因素，比单纯依靠管径分配或者管径管长的关系分配要更加平稳.

2.3管网平差计算

管网平差[7]计算采用传统的解环方程组方法，即哈代-克罗斯法.平差时，对平差的次数进行限定，对不满足条件的管径组合进行大比例的惩罚，直至被淘汰.初始流量分配采用自动分配方法，最大程度上保证计算数据的合理性.管网的起始点信息、本环邻环信息、管段长度信息和节点流量信息通过文本直接由程序读取，可提高程序运行的效率并节约时间.

2.4管网优化计算步骤

管网优化的流程图如图1所示.

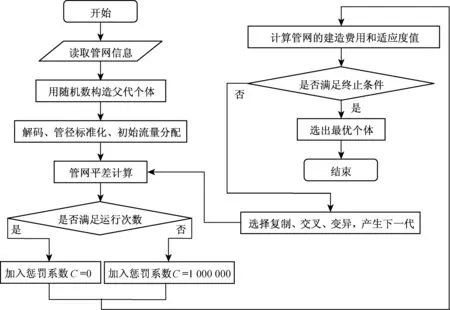
图1　管网优化的基本流程图Fig.1　The basic flow chart of pipe network optimization

3　实例研究

3.1研究实例的定线草图

实例的定线草图如图2所示，管网基本信息已附图中.通过编程，对图2进行基于经济流速先验信息启发式遗传算法计算，求出其最优的管径组合.

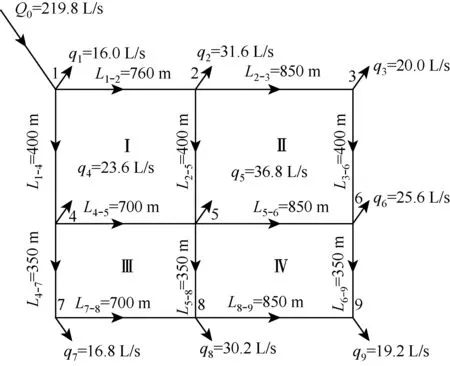
图2　管网计算示意图Fig.2　Calculation diagram of pipe network

3.2程序运行赋值

由于程序自动从输入的txt文档中读取数据进行运算，赋值步骤如下：

第一步依次输入节点数加1值、管段数加1值、环数加1值及管网总流量，即分别为10 ，13， 5， 219.8；

第二步依次输入管网草图中基本信息，即起点、终点、本环、邻环编号及管段长度，详见表1所示;

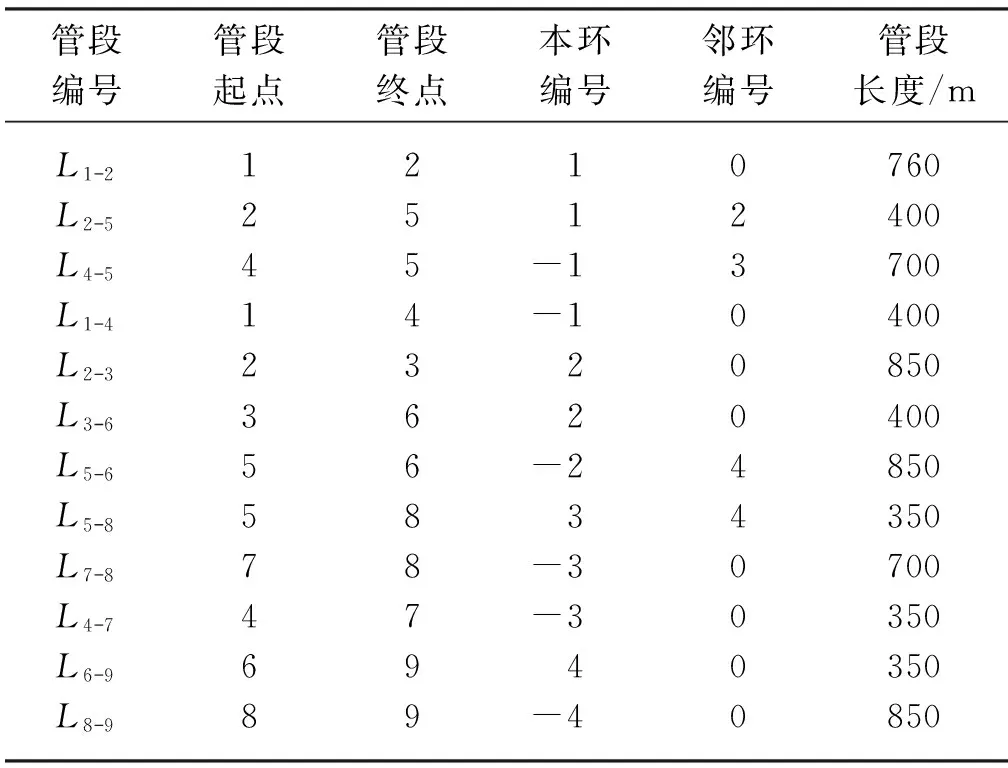
表1　管网计算赋值表Table 1　Assignment table of network computing

第三步依次输入各节点的集中输出流量，即16.0，31.6，20.0，23.6，36.8，25.6，16.8，30.2，19.2L/s.

3.3管网优化计算

程序进行计算时，部分参数设为：a=12，b=372，α=1.7[5-7]；电费E=0.5元/(kW·h).

对程序采用不同的交叉率和变异率，经多次运行，以得到最优的管径组合，并记录该最优的管径组合所优化管网的最优解.根据经济流速进行估算，大致求出合适的管径，供作参考.基于经济流速先验信息的启发式算法和标准遗传算法的适应度与迭代次数的关系如图3所示；基于经济流速先验信息的启发式算法、标准遗传算法和基于经济流速估算结果的对比如表2所示.

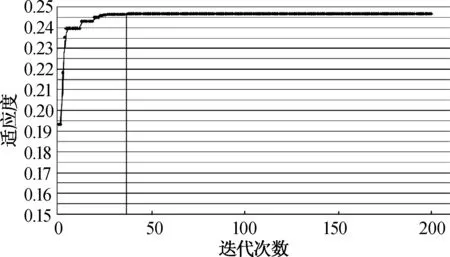
(a) 基于经济流速先验信息的启发式算法

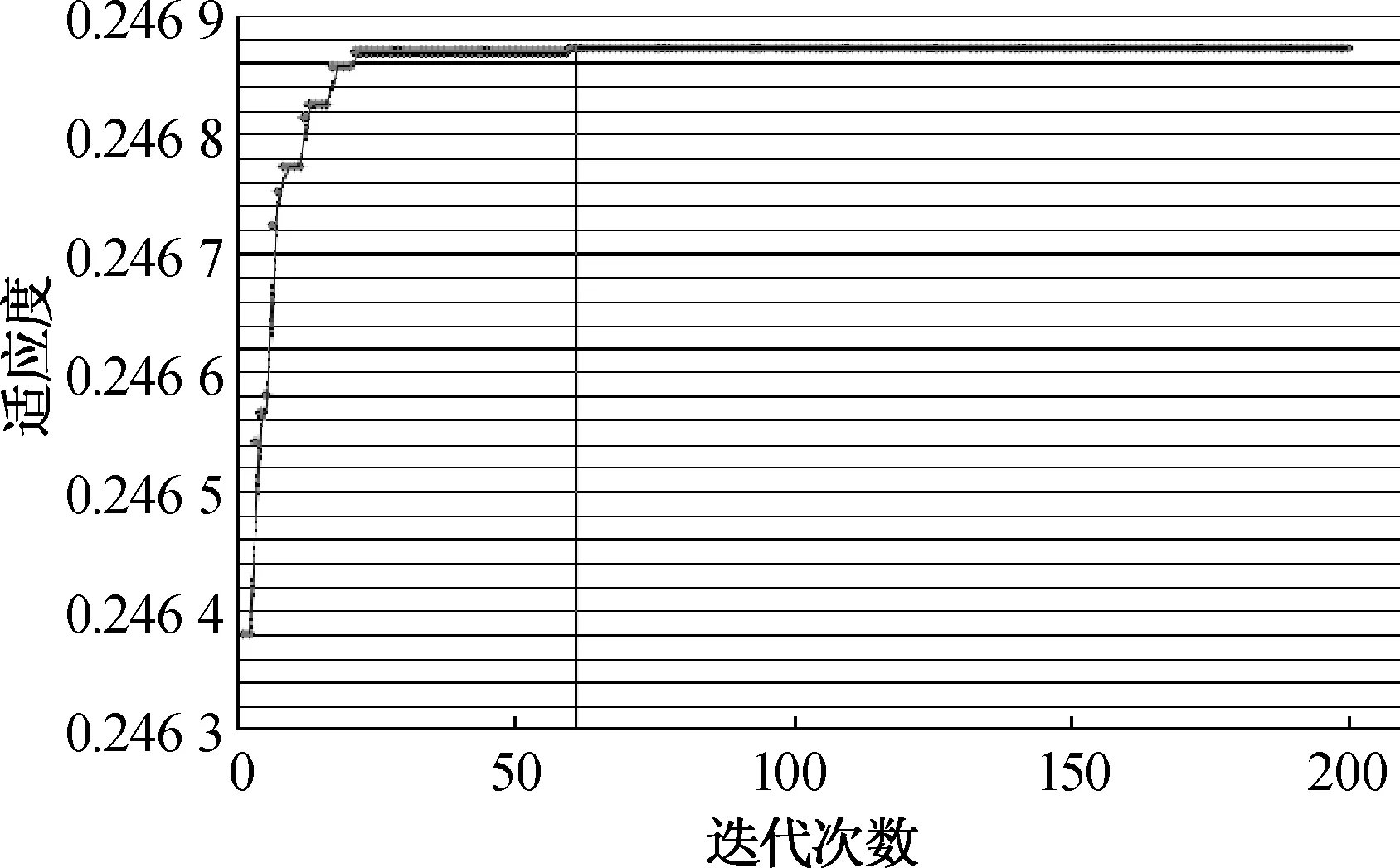
(b) 标准遗传算法图3　基于经济流速先验信息的启发式算法与标准遗传算法的适应度与迭代关系图Fig.3　The diagram of fitness iteration relationship between heuristic algorithm based on prior information of economic flow and standard genetic algorithm

由图3可以看出，基于经济流速先验信息启发式算法和标准遗传算法的收敛程度都非常好.经过多次不同变异率和交叉率的测试，基于经济流速先验信息启发式算法计算的适应度较标准遗传算法的变化范围大，在一定程度上避免了程序收敛于局部的最优解，保障了程序运行结果的可靠性.

管网的优化计算是一项复杂繁琐的工作.从表2可以看出，基于经济流速先验信息启发式算法和标准遗传算法的管网造价费用计算结果相差不多，几乎没什么区别，但从管径组合的合理性和管内流速的大小而言，基于经济流速先验信息的启发式算法的结果更加合理.同时，前面两种优化算法计算管网造价的费用都要比基于经济流速估算得到的费用低6.43%左右，由此可以说明前面两者优化算法的有效性.

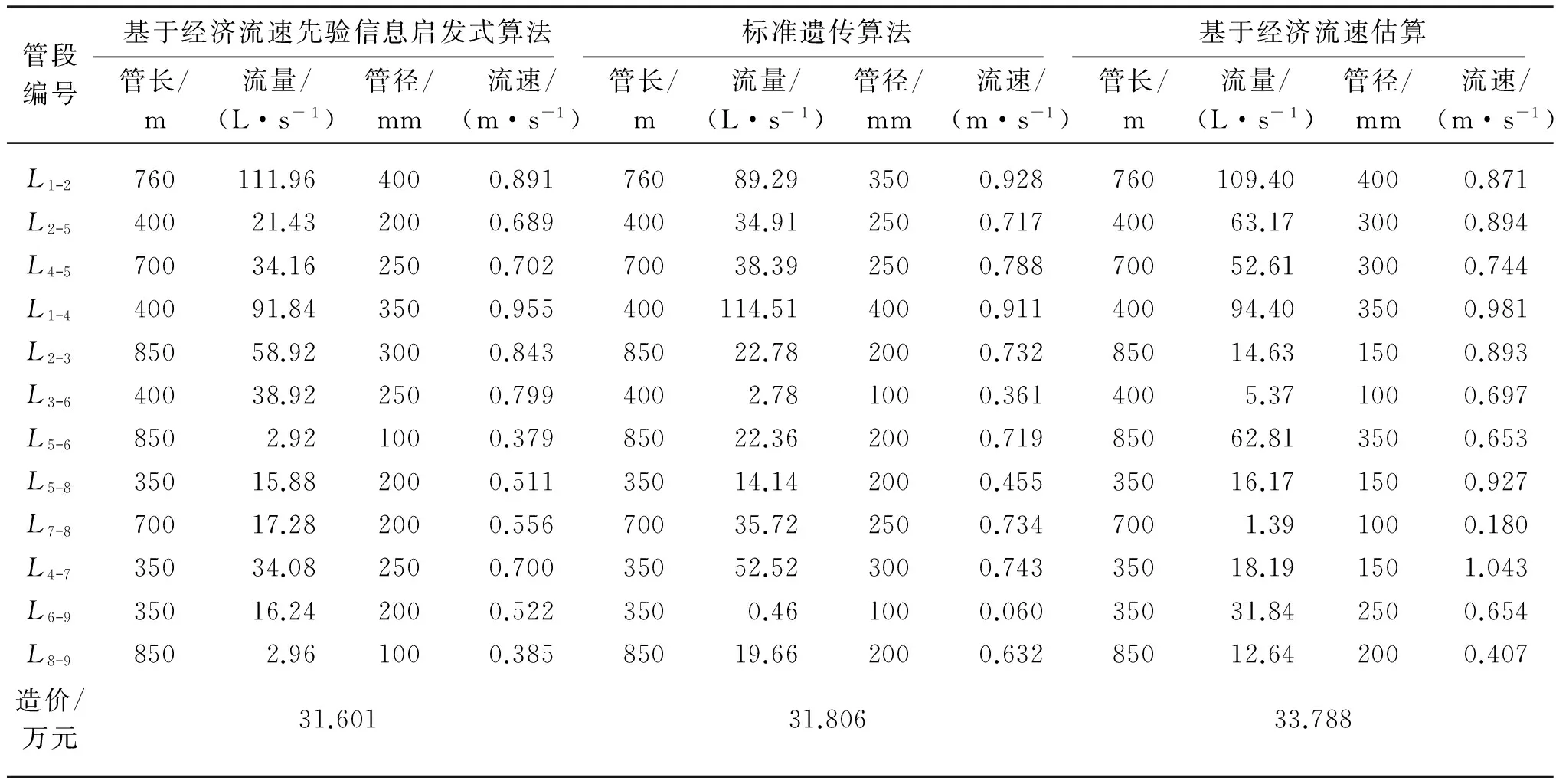
表2　基于经济流速先验信息的启发式算法、标准遗传算法和基于经济流速估算的计算结果对比Table 2　The calculation results of heuristic algorithm based on prior information of economic flow,standard genetic algorithm and estimation based on economic flow

遗传算法具有随机搜索特性，因而能够得到全局最优解.基于经济流速先验信息启发式算法在发挥遗传算法有效性的同时，对流速、流量进行约束，充分利用前人计算结果，即经济流速，从而大大提高了程序的寻优效率.程序计算的实例是一个具有代表性的四环管网，可以更改管网的一些基本参数，并在不同的交叉变异率的条件下进行多次运行，能够对中小型管网进行优化计算，也可以作为严格优化算法的初始解[8].

4　结　语

本文采用基于经济流速先验信息的启发式算法进行环状管网优化设计，既避免了手工近似计算时产生的巨大工作量，又能使计算结果更加精确，同时还能获得多种方案，以便进行比较，从而获得更加合理的设计方案.实际应用时，为保证能够得到最优结果，可以采用不同的交叉率和变异率，多次运行程序，选取管网造价最经济、符合实际情况的方案作为最终的设计方案.但本文在管网优化计算时，对模型的约束条件考虑得较少，因而并不能很好地保证供水系统最经济.因此，该优化模型还存在一定的局限性，后续将进一步深入研究，以便建立更加合理的数学模型.

[1] 严煦世,范瑾初.给水工程[M].北京:中国建筑工业出版社,1999.

[2] 唐穗欣.标准遗传算法的原理及算例[J].软件导刊,2007(1):100-101.

[3] 金菊良,丁晶.水资源系统工程[M].成都:四川科学技术出版社,2002.

[4] 董深,吕谋,陆海.基于遗传算法给水管网优化模型的改进研究[J].中国给排水,2007,23(17):87-90.

[5] 赵洪宾.给水管网系统理论与分析[M].北京:中国建筑工业出版社,2003.

[6] 况青松.改进的遗传算法在给水管网设计中的应用[D].合肥:合肥工业大学土木与水利工程学院,2003.

[7] 王国明.给水管网的平差与优化[J].化工给排水设计,1994(3):11-14.

[8] 陈玲俐,叶志明,李杰.基于经济流速的管径优化方法[J].上海大学学报,2005,11(2):196-200.

Optimal Design of Heuristic Pipe Network Based on Prior Information of Economic Flow Rate

DINGKun1,ZHANGJia1,ZHANGMing2,JINJu-liang3，ZHANGYong1

(1. College of Environment and Energy Engineering, Anhui Jianzhu University, Hefei 230601,China;2. College of Civil Engineering and Architecture, Anhui Polytechnic University ，Wuhu 241000，China；3. College of Civil Engineering, Hefei University of Technology, Hefei 230009, China)

In order to solve the problems such as large computation error and low optimizing efficiency of conventional genetic algorithm in water supply networks design, a series of improvements are adopted, including economic velocity restraint, volume restraint and penalty function. And on this basis, the heuristic optimizing method is proposed based on prior information of economic flow. It is proved that the method can improve the convergence rate and optimizing efficiency of genetic algorithm and gain considerable accurate commutated result. Furthermore, pipeline networks design based on this method is more reasonable and low in engineering investment.

water supply networks; optimal design； economic flow; economic pipe diameter; penalty function; genetic algorithm

1671-0444(2015)03-0387-05

2014-07-08

国家自然科学基金资助项目(21171004);安徽省教育厅自然科学基金资助项目(KJ2011z059)；安徽省年度攻关资助项目(11070403050)；安徽省教育厅教研资助项目(2013YX17)

丁琨(1968—),男,安徽安庆人,副教授,硕士,研究方向为城市给水排水和环境工程. E-mail：874408959@qq.com

TU 991.33

A