跳扩散环境下红利支付对不确定厌恶投资者最优投资组合选择的影响

梁　勇,费为银，方和远，刘　鹏

(安徽工程大学 数理学院,安徽 芜湖 241000)

跳扩散环境下红利支付对不确定厌恶投资者最优投资组合选择的影响

梁勇,费为银，方和远，刘鹏

(安徽工程大学 数理学院,安徽 芜湖 241000)

面对例外事件的冲击，金融市场的股票价格会发生跳跃，当股票价格发生跳跃且支付红利时，不确定厌恶投资者的预期效用的刻画将会采用不同于传统的方法.利用跳扩散型随机微分方程理论和动态规划方法,建立了不确定厌恶投资者的最优投资策略所满足的Hamilton-Jacobi-Bellman (HJB)方程.进一步，利用市场分解的技术求解HJB方程,从而推导出最优消费与投资策略.最后，利用数值分析定量地讨论了投资者风险厌恶因素对最优决策的影响.

不确定厌恶；跳扩散型随机微分方程；最优投资组合；例外事件；红利支付

自文献[1]提出连续时间下的最优消费与投资模型框架以来，国内外学者就不同条件下的最优消费投资模型作了广泛的研究.文献[2-3]探讨了双跳下的资产定价问题.近年来，许多学者分析认为，除了考虑传统的不确定外，还需考虑奈特不确定对投资者投资决策的影响[4-5].文献[6]建立了连续时间多先验效用的跨期模型.文献[7]研究了有关跳的不精确信息下的资产定价．利用稳健性方法，文献[8]分析了动态资产分配问题.在包含多资产跳扩散框架下，文献[9]调查了最优投资组合问题.文献[10]研究了在奈特不确定下的最优消费投资问题.文献[11]利用倒向随机微分方程和Malliavin分析技术，讨论了最大最小预期效用的加权平均标准下的最优消费投资问题.文献[12]研究了考虑退休和闲暇的奈特不确定投资者的最优消费投资问题.基于通胀和跳环境，文献[13]分析了通胀对跳暴露和扩散暴露的影响.另一方面，由文献[14]研究结果可知，红利对投资者的最优消费和投资决策也会产生影响.在文献[13-15]的研究基础上,本文进一步讨论风险股票支付红利时奈特不确定投资者的期望效用最大化问题.根据跳扩散型随机微分方程和动态规划方法推导出相应的Hamilton-Jacobi-Bellman (HJB)方程，并利用市场分解技术得到解析解.最后，通过数值模拟说明投资者的风险厌恶对最优决策的影响，所得结论具有一定的经济意义.

1　跳扩散模型

本节讨论连续时间不完备金融市场，股票价格由多维跳扩散过程加以刻画，时间跨度是[0,T].设(Ω,F,P)是一个完备的概率空间.产生经济状态的不确定主要是由于概率空间(Ω,F,P)上的d-维标准布朗运动和(n-d)维的多元泊松过程N(t)=(N1(t),N2(t)，…,Nn-d(t))T,其中Nk(t)表示在时间为t时第k类跳的数量.在经济状态中通过自然域流给定信息流,即右连续的增广域流:,t∈[0,T]}，其中.假设可观测事件是在最后获得,即F=FT.设Nk(t)第k类跳的幅度为Jk，而随机强度为λk(t),Jk概率密度为Φk(t,dx),λk(t)为非负的且Ft- 是可料的，第k类跳的大小所有可能取值的空间用Ek表示.设Ek=(0,∞)，Ek=(-1,0)，Ek=(-1,∞)分别为正、负和混合跳的大小所有可能取值的空间.

设某投资者的效用是不变相对风险厌恶(CRRA)的,且初始财富为W0,其交易策略为π(t)=(π1(t),π2(t)，…,πn(t)),πi(t)表示投资者在t时刻持有第i个股票的比例.投资者的财富过程Wt满足动力学：

dWt=[r+π(t)(b(t)+δ-r1)]Wtdt+

Wtπ(t)Σb(t)dB(t)+

Wt -π(t-)Σq(t)(J·dN(t))-C(t)dt

其中：Σb表示n×d型的矩阵；Σq表示n×(n-d)型的矩阵；C(t)表示t时刻的消费率；δ=(δ1,δ2，…,δn)T表示红利支付率向量，1表示分量为1的n维向量.在投资组合π中,金融市场上的扩散和跳风险暴露分别用πΣb和πΣq表示.

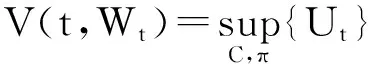
其中：Σq k表示Σq的第k列,.易知，存在一个ξ*使得测度P(ξ*)是最优解,则

其中：H(ξt)≥0.当ψ(x)=(1-γ)x时,

假设考虑两种极端情况,即φ=0和φ=∞.当φ=0时,说明投资者是含糊中性的；当φ=∞时,说明投资者是极端谨慎的.

假设可逆矩阵Σ表示n×n型的矩阵(Σb,Σq).设金融市场中的扩散和跳风险πb=(πb1,πb2,…,πbd)和πq=(πq1,πq2,…,πq(n-d))分别表示πΣb和πΣq.

由于π=πΣΣ-1=π[Σb,Σq]Σ-1=(πb,πq)Σ-1,所以通过最优暴露πb和πq的求解即可获得最优投资组合π.假设下式为相对风险溢价

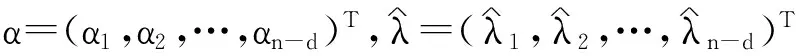
注意到π*是由(n-d+1)个金融市场的最优投资策略组成的向量通过矩阵Σ-1旋转得到，其中，第一个是纯扩散金融市场,有一个无风险资产,d个股票价格服从

dSD(t)=SD(t-)((vb+r1)dt+dBS(t))

而且效用函数为

文献[13,15]考虑了极端事件引起跳发生的情形，而本文假设仅考虑跳为负的情况下(对跳为正的情形可类似讨论)，其中，表示参考模型中跳的大小的参数估计.

为了简便,将原始的非完备的跳扩散金融市场分解为一个完备的纯扩散金融市场和一族单期的纯跳金融市场，这里假设纯扩散金融市场是完备的.通过计算值函数V(t,W)可以得到下面的命题1和2.它们的证明类似文献[15]中的命题1和2，其中，以下和如文献[15]的命题1中式(14)～(16).

命题1投资者的最优值函数V(t,Wt)为

其中:

其中:

2　数值分析

为了讨论问题的方便，选取了两个股票和一个无风险资产作为投资组合进行数值分析.

设n=2,d=1,φ

由命题1和2中的公式可得图1.由图1可以看出，一个风险资产权重π1随着风险厌恶系数γ的增加而减少，而另外一个风险资产权重π2随着风险厌恶系数γ的增加而增加.由于本文假设股票价格向下跳，所以投资者通过两个股票的做多与做空来对冲股票价格向下跳的风险，同时发现，随着风险厌恶系数的不断增加,投资含有例外事件冲击股票的投资绝对比例就会不断下降，表现在图1中的两条曲线都趋于横轴，而且，随着风险厌恶程度单调下降接近0，投资者在风险资产上的头寸迅速减少.

图1　γ对投资组合权重π的影响Fig.1　The effect of γ on portfolio π

3　结　语

本文研究了在例外事件冲击下红利支付对不确定厌恶投资者的最优投资组合选择问题的影响.由于例外事件引起过程的跳跃，所以可以利用跳扩散型随机微分方程来刻画资产价格，利用相应的理论建立不确定厌恶投资者的随机动态模型.为此，首先建立了资产价格带跳扩散的随机动力学方程.其次,描述了不确定厌恶投资者带有中期消费和终端财富的预期效用最大化问题,其中的效用函数体现了投资者的模型不确定厌恶.进而，利用跳扩散随机微分方程理论与动态规划原理推导出HJB方程，再根据市场分解方法获得不确定厌恶投资者的最优投资决策.最后，利用数值模拟分析了投资者的风险厌恶对最优组合投资策略的影响.本文所得结论为投资者决策提供较为现实的经济参考价值.

[1] MERTON R C.Optimum consumption and portfolio rules in a continuous-time model[J].Journal of Economic Theory,1971,3(4):373-413.

[2] DUFFIE D,PAN J,SINGLETON K.Transform analysis and asset pricing for affine jump-diffusions [J].Econometrica,2000,68(6):1343-1376.

[3] LIU J,LONGSTAFF F,PAN J.Dynamic asset allocation with event risk[J].Journal of Finance,2003,58 (1):231-259.

[4] GILBOA I,SCHMEIDLER D.Maxmin expected utility with non-unique prior[J].Journal of Mathematical Economics,1989,18 (2):141-153.

[5] KNIGHT F H.Risk,uncertainty,and profit[M].Boston: Houghton Mifflin,1921.

[6] CHEN Z J,EPSTEIN L G.Ambiguity,risk and asset returns in continuous time[J].Econometrica,2002,70 (4):1403-1443.

[7] LIU J,PAN J,WANG T.An equilibrium model of rare -even premia[J].Review of Financial Studies,2005,18 (1):131-164.

[8] MAENHOUT P.Robust portfolio rules and asset pricing[J].Review of Financial Studies,2004,17 (4):951-983.

[9] AIT-SAHALIA Y,CACHO-DIAZ J,HURD T.Portfolio choice with jumps: A closed-form solution[J].Annals of Applied Probability,2009,19 (2):556-584.

[10] FEI W Y.Optimization consumption and portfolio choice with ambiguity and anticipation[J].Information Sciences,2007,177 (23):5178-5190.

[11] FEI W Y.Optimal portfolio choice based onα-MEU under ambiguity[J].Stochastic Models,2009,25 (3):455-482.

[12] FEI W Y.Optimal consumption-leisure,portfolio and retirement selection based on α-maxminexpected CES utility with ambiguity[J].Applied Mathematics: A Journal of Chinese University,2012,27 (4):435-454.

[13] 费为银，夏登峰，刘鹏.模型不确定和极端事件冲击下带通胀的最优投资组合选择问题研究[J].应用概率统计，2014,30 (3):322-336.

[14] 李钰，费为银，石学芹，等.在部分信息下股票收益服从隐马尔科夫模型的最优交易策略[J].东华大学学报：自然科学版，2012,38 (6):758-762.

[15] 费为银，刘鹏,夏登峰.极端事件冲击下含糊厌恶投资者的最优投资组合选择问题研究[J].中国科学技术大学学报，2014,44 (9):475-482.

Impacts of the Dividend Payment on the Optimal Portfolio Choice of an Investor with the Ambiguity Aversion under Jump-Diffusion

LIANGYong,FEIWei-yin,FANGHe-yuan,LIUPeng

(School of Mathematics and Physics,Anhui Polytechnic University,Wuhu 241000,China)

The stocks’ prices in a financial market will jump when there is a shock of an rare event.And the utility of an ambiguity aversion investor with the environment of both the stock price’s jump and the dividend payment is characterized by a new method.Through the theory of jump-diffusion stochastic differential equations and the dynamic programming principle,the value function of an investor’s optimal consumption and portfolio satisfying the Hamilton-Jacobi-Bellman (HJB) equation is derived.Moreover,market decomposition technique is applied to solve the HJB equation,the optimal consumption and portfolio policy for investors is obtained.Finally,the effects of the risk aversion on the optimal portfolio choice of an investor are analyzed by numerical simulation.

ambiguity aversion；jump-diffusion stochastic differential equations；optimal portfolio；rare events；dividend payment

1671-0444(2015)02-0273-04

2014-05-05

国家自然科学基金资助项目(71171003)；安徽省高校自然科学基金资助项目(KJ2012B019，KJ2013B023)

梁勇(1981—)，男，安徽马鞍山人，硕士，讲师，研究方向为金融数学与金融工程.E-mail: liangyong@ahpu.edu.com

O 211.63；F 224.9

A