双向拉伸下的纬平针织物线圈形态分析
谢 娟,龙海如
(东华大学 纺织学院,上海 201620)
双向拉伸下的纬平针织物线圈形态分析
谢娟,龙海如
(东华大学 纺织学院,上海 201620)
采用二维线圈结构模型,计算纬平添纱针织物的针编弧、圈柱和沉降弧在双向拉伸下的长度变化,进而分析线圈形态变化和纱线转移情况.实验结果表明:在横向拉伸、纵向高度不变的双向拉伸下,圈弧长度增加,圈柱长度减少,纱线由圈柱向圈弧转移;在纵向拉伸、横向宽度不变的双向拉伸下,圈弧长度减少,圈柱长度增加,纱线由圈弧向圈柱转移.理论结果和实验结果具有较好的一致性,表明此二维线圈结构模型可以用于分析和预测纬平针织物在双向拉伸下线圈形态变化和纱线转移.关键词: 纬平针织物;双向拉伸;线圈模型;纱线转移
对纬平针织物的结构和变形理论研究已达半世纪之久.学者们通过建立针织物几何结构模型[1-7]分析了针织物线圈在未拉伸条件下的结构形态,如文献[1]首次提出了针织物线圈由直线和圆弧组成的观点;文献[7]采用弹性杆理论分析了针织线圈的三维结构模型.但这些理论缺乏对针织物拉伸性能的分析.由于在生产和实际服用的过程中,纬编针织物经常受到多方向同时拉伸,如平面内的双向或多向拉伸与剪切,服装肘部、肩部等弯曲部位的受力变形.为了分析测试针织物的实际受力情况,从20世纪60年代开始,已有学者开始研究针织物在多向和双向拉伸条件下的性能变化[8-14].其中在对针织物的双向拉伸研究中,文献[8]提出了一种用于计算分析针织物的双向拉伸性能的理论方法,并解释了针编弧和沉降弧由弯曲到拉直过程中的长度变化.文献[9]提出了一个六边形线圈模型,并用有限元法计算模拟了织物在双向拉伸变形后的形态.文献[10]根据弹性杆理论,预测针织物在双向拉伸条件下的力与应变关系.文献[12-13]对针织物在双向拉伸下的黏弹性和滞后性进行了研究.
然而,上述模型并未对针织物线圈在双向拉伸过程中其圈弧、圈柱的长度变化进行分析计算.本文通过综合运用上述的几何结构模型和力学模型,分析纬平针织物在双向拉伸条件下其针编弧、圈柱和沉降弧的长度变化,探讨其线圈形态改变和纱线转移情况,以便为预测针织物在双向拉伸条件下的力学性能提供参考.
1 纬平针织物的双向拉伸
针织物的双向拉伸分为两种: 第一种为一向固定,另一向拉伸(strip biaxial elongation,SBE),具体可分为横向拉伸纵向高度维持不变(SBE-X)和纵向拉伸横向宽度保持不变(SBE-Y)两种情况;第二种为横向和纵向同时拉伸.
针织物在双向拉伸过程中,经历两个阶段:(1)线圈中纱线形态的改变,即在小应变时,纱线由弯曲态逐渐到完全伸直状态的改变;(2)纱线长度的改变,即完全伸直的纱线长度开始增加,发生伸长.此外,在整个拉伸过程中,纱线在线圈的交织点发生“滑移”.假设在整个拉伸过程中,织物的每个线圈的形态与结构完全均匀和对称.
2 线圈结构模型
2.1未拉伸状态下的线圈结构模型
纬平针织物线圈在未拉伸状态下的形态结构图1所示.线圈的针编弧和沉降弧分别是直径为a0和D的两个半圆弧纱段.其中,a0为两个圈柱轴线之间的最大距离;θ0为圈柱与横列方向的夹角(0°<θ<90°);A0(mm)和B0(mm)分别为针织物在未拉伸状态下的圈距和圈高.
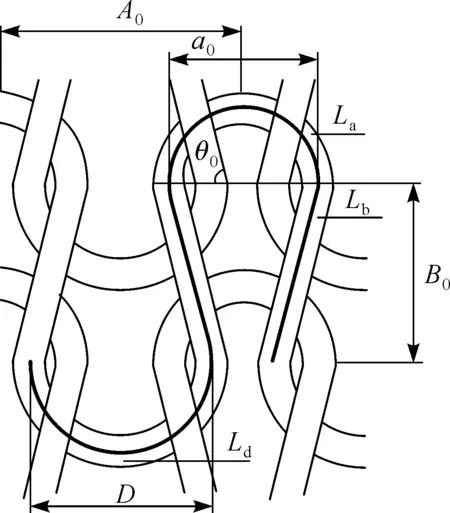
图1 未拉伸状态下针织线圈结构图Fig.1 The loop structure in initial state
针编弧La(mm)、沉降弧Ld(mm)和圈柱Lb(mm)的理论计算式如式(1)所示,其中PA和PB分别为针织物的横密(纵行/50 mm)和纵密(横列/50 mm),L0为线圈的初始长度.
(1)
2.2双向拉伸状态下的线圈结构模型
针织物在SBE-X和SBE-Y双向拉伸状态下的线圈结构形态如图2所示.
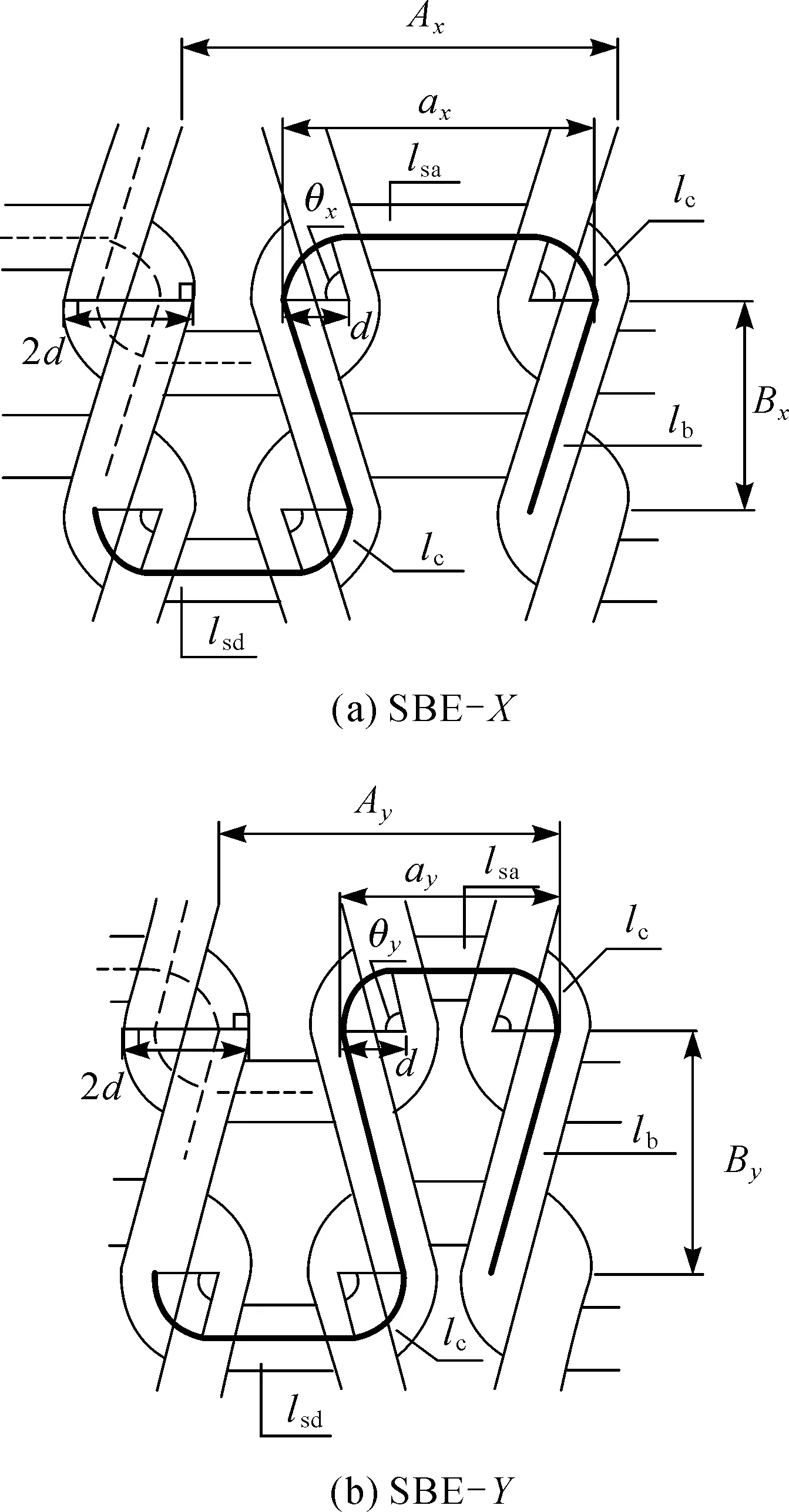
图2 双向拉伸针织线圈结构图Fig.2 The loop structure under strip biaxial elongation
假设:(1)线圈的针编弧和沉降弧分别由位于两个交织点之间的直线纱段ls(即针编弧中的lsa及沉降弧中的lsd)和交织点处的两个弯曲纱段lc组成.(2)在拉伸过程中,相邻线圈始终在“交织点”处紧密接触,串套处纱线轴向水平间距为纱线的直径d.由于小应变拉伸,纱线直径及纱线在交织点处的弯曲曲率变化甚微,故假设弯曲纱段lc长度不变.(3)在横向拉伸、纵向高度不变(SBE-X)的情况下,圈距Ax和ax均随横向应变εx的增加而线性增加,圈高Bx保持不变;在纵向拉伸、横向宽度不变(SBE-Y)的情况下,圈距Ay保持不变,圈高By和ay均随纵向应变εy的增加而线性增加.α和β分别为a与应变ε在SBE-X和SBE-Y中的比例系数,可根据实验测量值拟合计算求得.(4)由于本文将研究纬平针织物在一向固定、另一向拉伸的双向小应变情况下的线圈形态变化,在拉伸过程中,纱线是由初始态到伸直态的变化,不发生伸长,且每个线圈的长度L0保持不变.
SBE-X和SBE-Y拉伸下线圈各纱段的理论计算式如式(2)和(3)所示,其中Lx和Ly分别为相应的线圈长度.
(2)
(3)
由于线圈长度在整个拉伸过程中保持不变,故有L0=Lx=Ly,得到式(4).
(4)
令
(5)
其中t≥1,将式(5)代入式(4)中得到式(6)
(6)
将横向应变εx和纵向应变εy的实验结果代入式(6)中,可以求解出相应的tx与ty值.
将式(5)分别代入式(2)和(3),得到线圈针编弧La、圈柱Lb和沉降弧Ld在SBE-X和SBE-Y拉伸条件下的理论计算式如式(7)和(8)所示,据此进而可以预测针织物的线圈在双向拉伸条件下的纱线转移情况.
(7)
(8)
3 实 验
实验所用试样为在SANTONI SM8 Top2无缝内衣机上编织而成的添纱纬平针织物,其组织结构如图3所示,面纱1为78 dtex/48 F 锦纶长丝纱,地纱2为44 dtex/12 F锦纶/33 dtex氨纶包芯纱.试样的尺寸为16 cm×16 cm,横密为80纵行/5 cm,纵密为130横列/5 cm.
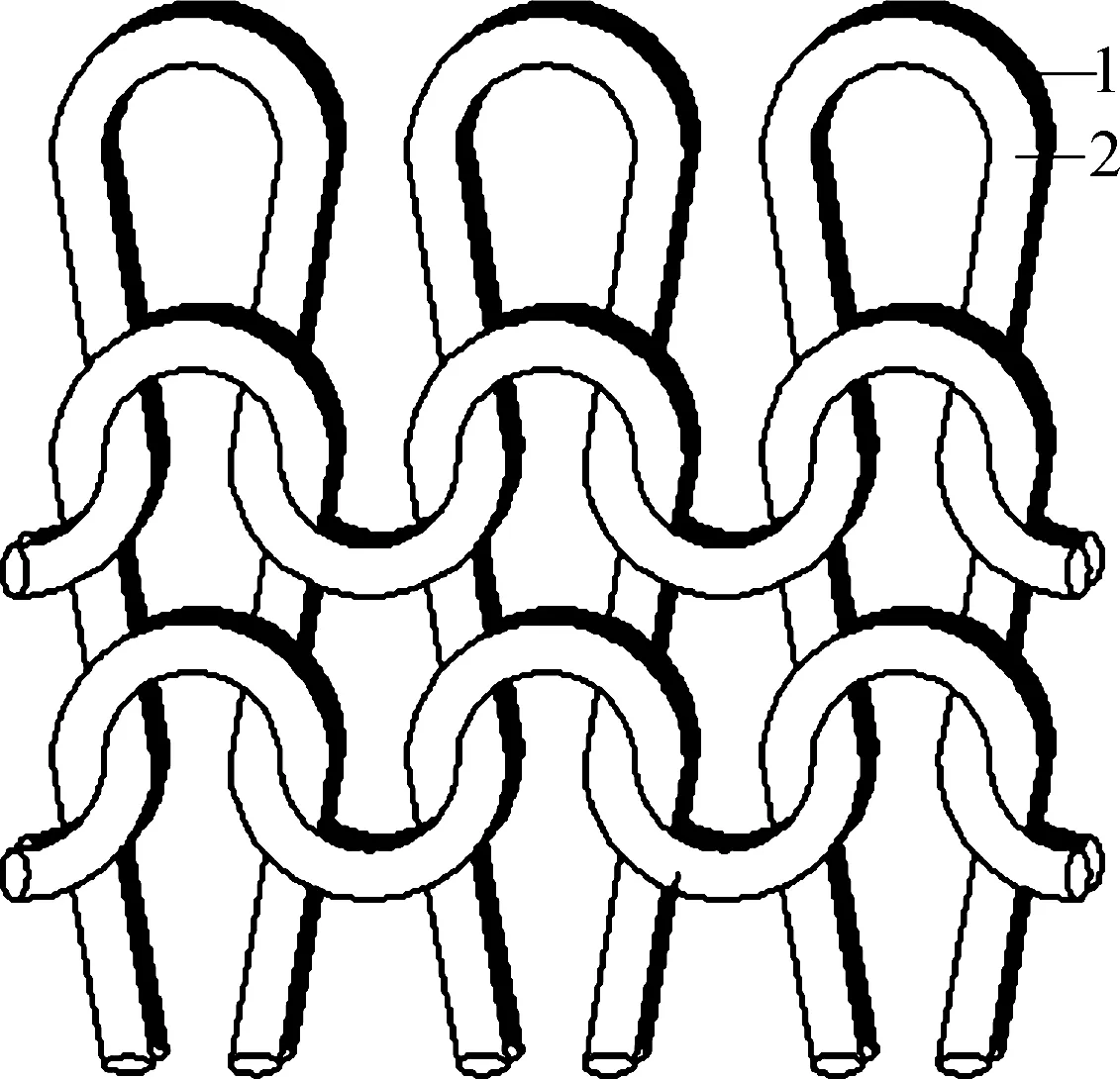
图3 试样的线圈结构组织Fig.3 Loop structure of specimen
试样在双向拉伸条件下的拉伸力与应变值由温州大荣的X-Y双向强力仪测得.设定拉伸速度为60mm/min,预加张力为0.1N,当试样在拉伸方向的应变达到30%时,实验结束.在整个拉伸过程中,试样的线圈形态实时变化由SONYDCR-SR200E摄像机记录.在SBE-X和SBE-Y拉伸下,应变为0%,15%和30%时试样的形变图分别如图4和5所示.

(a) =0%

(b) =15%

(c) =30%图4 SBE-X拉伸下试样在不同形变时的形变图Fig.4 Deformation of specimens at various strain under SBE-X

(a) =0%

(b) =15%

(c) =30%图5 SBE-Y拉伸下试样在不同形变时的形变图Fig.5 Deformation of specimens at various strain under SBE-Y
4 实验结果与讨论
4.1拉伸力与应变测量

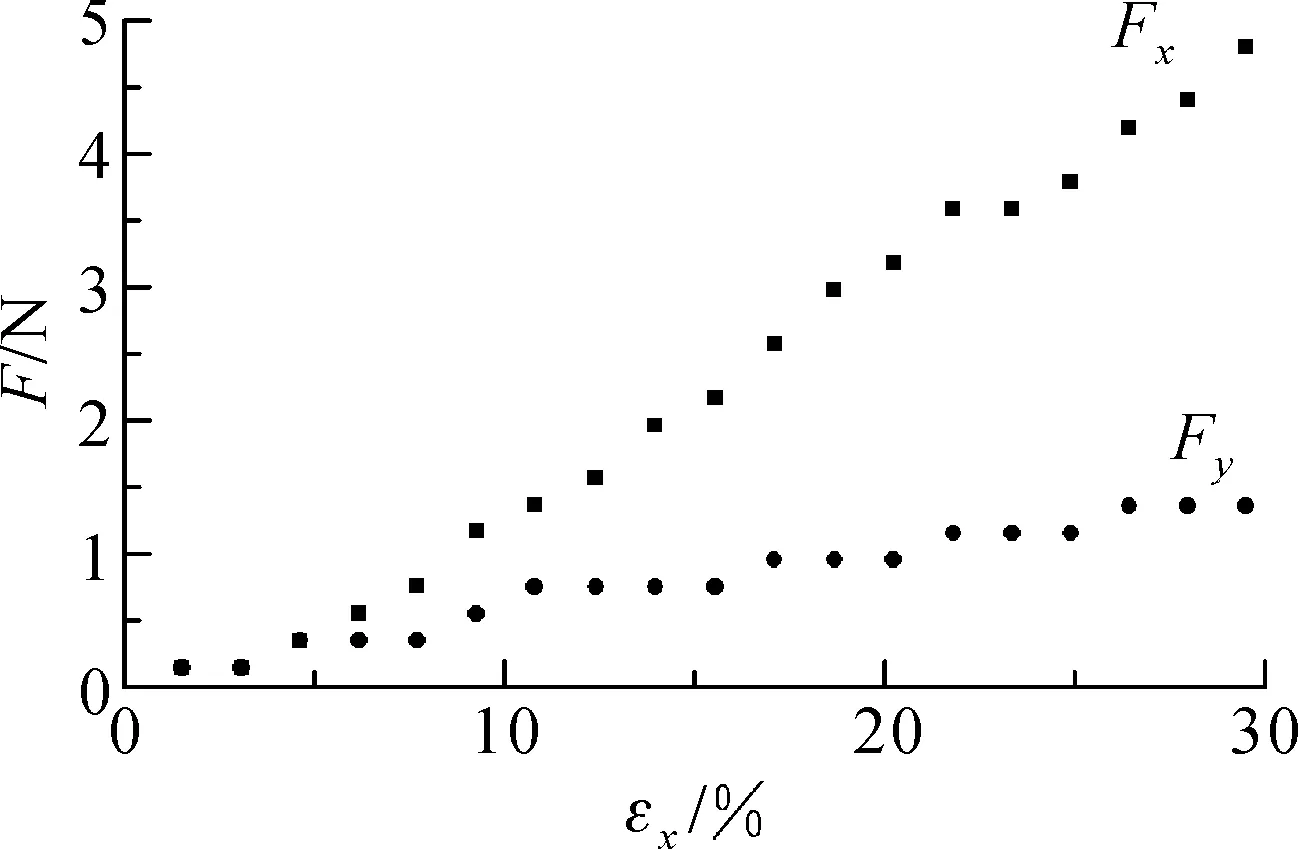
(a) SBE-X
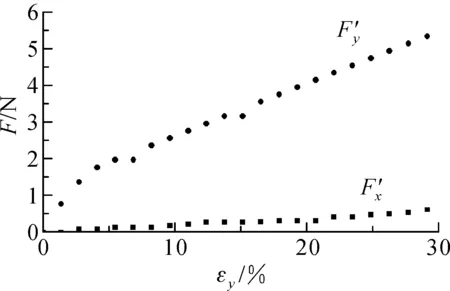
(b) SBE-Y图6 试样在双向拉伸下的拉伸力与应变关系Fig.6 The relationship between tensile force and strain of specimen under biaxial elongation
4.2线圈的针编弧、圈柱和沉降弧长度计算
实时拍摄线圈形态在双向拉伸过程中的变化,并从录像中选出不同应变下对应的帧.利用Matlab软件分析图像,测量多组线圈结构几何参数如d,θ,a,La,Lb和Ld等值,并取平均值.线圈在未拉伸状态下时,测量得a0,d,θ和L0分别为0.437 mm,0.12 mm,56°和2.725 mm.
圈柱最大间距在SBE-X和SBE-Y拉伸下的实测值如图7所示,通过对实验测量值的线性拟合分析(如式(9)所示),由式(9)可以直接读出,圈柱最大间距在两种拉伸下的线性系数α和β分别为0.5067和0.0340.
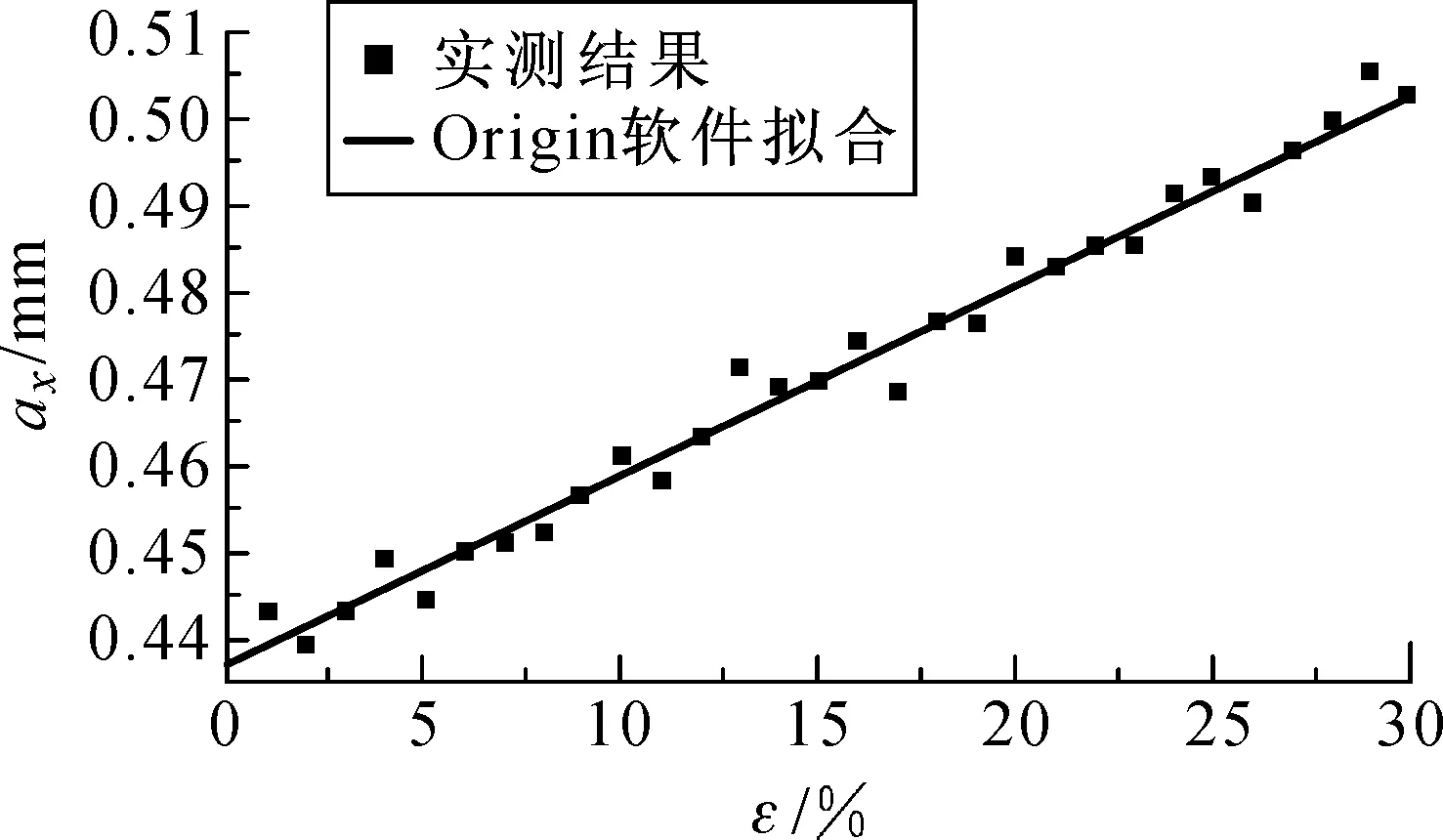
(a) SBE-X
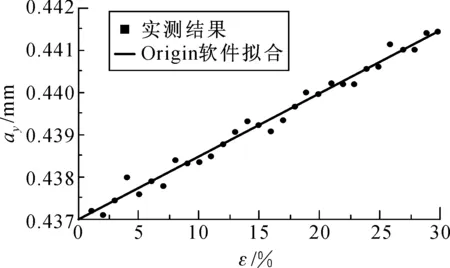
(b) SBE-Y图7 最大圈柱间距的实测值和理论拟合曲线Fig.7 The measured results and fitting curve of maximum space between two legs
(9)
将式(9)和应变ε的实验结果,以及根据实验值ε得到的t值代入式(7)和(8)中,可以得到针编弧La、圈柱Lb和沉降弧Ld分别在SBE-X和SBE-Y两种拉伸条件下的理论计算值.
La,Lb和Ld的实验测量值与理论计算值的对比如图8所示.由图8可以看出,在SBE-X拉伸条件下,线圈的针编弧和沉降弧都随着应变增加而增加,且沉降弧增长幅度大于针编弧的增长幅度,同时圈柱随着应变增加而降低,这说明纬平针织物在横向拉伸、纵向高度不变的双向拉伸中,纱线由圈柱向针编弧和沉降弧转移,以满足针织物在横列方向的延展.在SBE-Y拉伸条件下,线圈的针编弧和沉降弧随着应变增加逐渐减少,同时圈柱长度随着应变增加逐渐增加,这说明纬平针织物在纵向拉伸、横向宽度不变的双向拉伸中,纱线由圈弧向圈柱转移,以满足针织物在纵向的延展.由于La,Lb和Ld的理论值与实验测量值有较一致的变化趋势,因此,该二维线圈结构模型拥有较好的准确性,可用于预测和分析针织物在双向拉伸过程中的线圈形态变化和纱线转移情况.
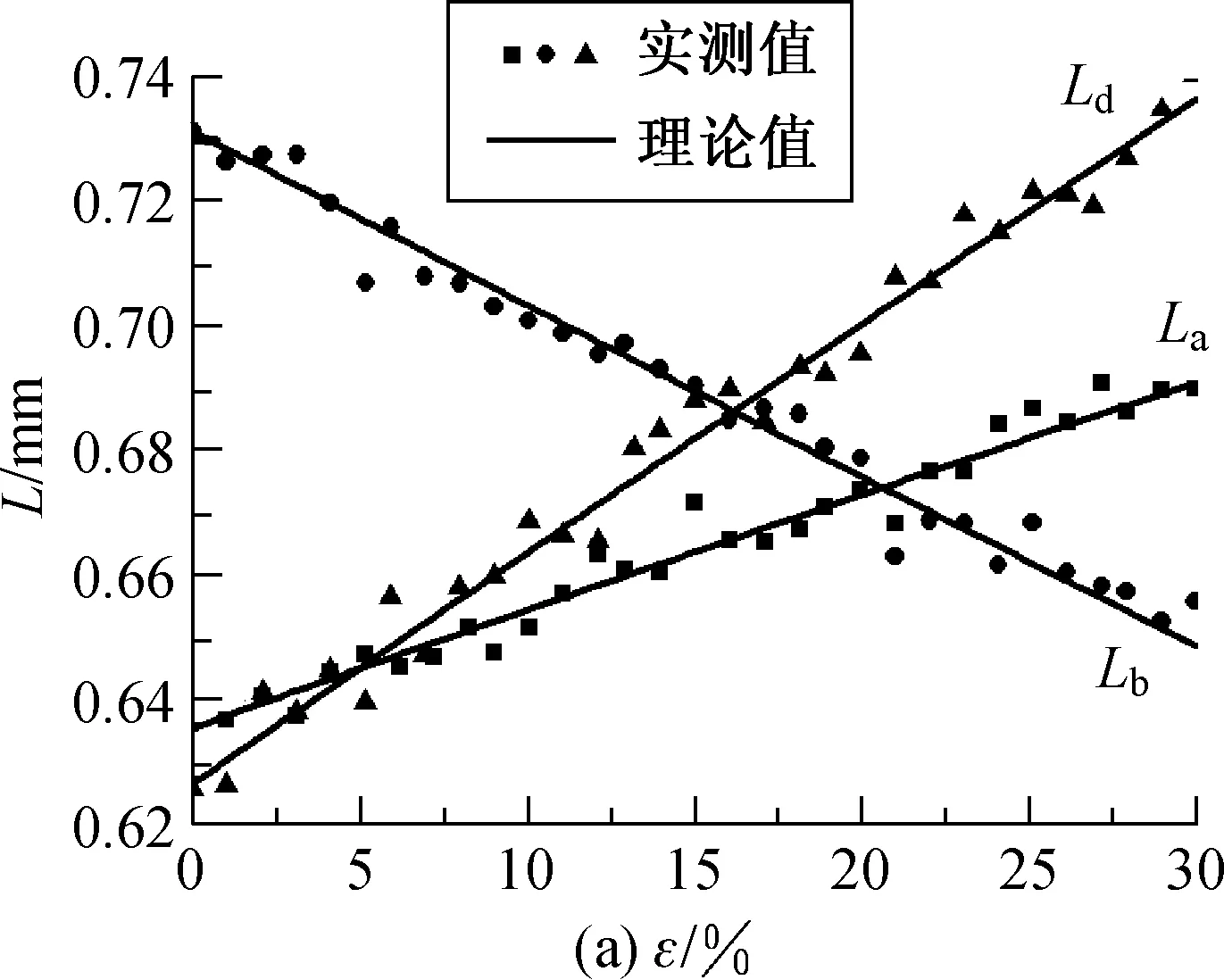

图8 针编弧、圈柱和沉降弧长度在双向拉伸下的实测值和理论计算值Fig.8 Experimental results and calculated data on the length of head loop,leg and sinker loop under biaxial elongation
5 结 语
本文建立了一个二维针织物线圈结构模型,用于计算在双向拉伸条件下纬平针织物的针编弧、圈柱和沉降弧的长度变化.实验结果和理论计算结果表明,在横向拉伸、纵向高度不变的双向拉伸下,线圈的纱线由圈柱向圈弧转移;在纵向拉伸、横向高度不变的双向拉伸下,线圈中的纱线由圈弧向圈柱转移.实验结果与理论曲线有较好的一致性,因此,所建立的模型具有较好的准确性和一致性,可用于计算和预测线圈形态的变化以及在双向拉伸过程中纱线转移情况.研究结果为针织物多向拉伸力学性能分析提供参考.
[1] PEIRCE F T.Geometrical principles applicable to the design of functional fabrics[J].Textile Research Journal,1947,17(3):123-147.
[2] DOYLE P J.Fundamental aspects of the design of knitted fabrics[J].J Text Inst,1953,44(8):561-578.
[3] LEAF G A,GLASKIN A.The geometry of the plain knitted loop[J].J Text Inst,1955,46(9):587-605.
[4] LEAF G A.Models of the plain knitted loop[J].Journal of the Textile Institute Transactions,1960,51(2):49-58.
[5] SHINN W E.An engineering approach to jersey fabric construction[J].Textile Research Journal,1955,25(3):270-277.
[6] MUNDEN D L.The geometry and dimensional properties of plain-knit fabrics[J].J Text Inst,1959,50(7):448-471.
[7] AJELI S,JEDDI A A A,RASTGO A.A three-dimensional analysis of loop knit structure by using a property of the buckled-twisted elastic rod[J].J Text Inst,2009,100(2):111-119.
[8] CHOU T W,KO F K.Textile structural composites[M].New York:North Holland,1989:99-115.
[9] WU W L,HAMADA H,MEAKAWA Z.Computer simulation of the deformation of weft-knitted fabrics for composite materials[J].J Text Inst,1994,85(2):198-213.
[10] HU H,ARAUJO M D,FANGUEIRO R,et al.Theoretical analysis load-extension properties of plain weft knits made from high performance yarns for composite reinforcement[J].Textile Research Journal,2002,72(11):991-995.
[11] GILLES H,PHILIPPE B.Consistent mesoscopic mechanical behavior model for woven composite reinforcements in biaxial tension[J].Composites Part B: Engineering,2008,39(2): 345-361.
[12] MATSUO M,YAMADA T,ITO N.Stress relaxation behavior of knitted fabrics under uniaxial and strip biaxial excitation as estimated by corresponding principle between elastic and visco -elastic bodies[J].Textile Research Journal,2006,76(6):465-477.
[13] MATSUO M,YAMADA T.Hysteresis of tensile load strain route of knitted fabrics under extension and recovery processes estimated by strain history[J].Textile Research Journal,2009,79(3):275-284.
[14] 张一平.纬编针织物双向拉伸性能研究[D].上海:东华大学纺织学院,2011.
Analysis on Loop Shape of Plain Knitted Fabric under Biaxial Elongation
XIEJuan,LONGHai-ru
(College of Textiles,Donghua University,Shanghai 201620,China)
A two-dimensional loop structure model is proposed to calculate the length of head loop,leg and sinker loop of plain knitted fabric under biaxial elongation,and predict the loop shape change and yarn transfer during elongation process.The experimental results indicate that yarn transfers from leg to curved sections under strip biaxial elongation in course direction,while it transfers from curved sections to leg under strip biaxial elongation in wale direction.Good accordance between the theoretical data and measured results shows this model can be used to predict the loop shape change and yarn transfer of plain knitted fabric under strip biaxial elongation within acceptable accuracy.
plain knitted fabric; biaxial elongation;loop model; yarn transfer
1671-0444(2015)02-0183-06
2014-02-19
谢娟(1987—),女,河北邯郸人,博士研究生,研究方向为智能纺织品.E-mail: anna.jxie@gmail.com
龙海如(联系人),男,教授,E-mail: hrlong@dhu.edu.cn
TS 181
A

