地震荷载下广州海珠桥桥面响应模拟

刘　麟，郭　力，高文堃

地震荷载下广州海珠桥桥面响应模拟

刘麟，郭力，高文堃

（东南大学 土木工程学院，江苏南京 210096）

为了研究广州海珠桥桥面在地震荷载下的安全性能，根据《公路桥梁抗震设计规范》，借助大型有限元分析软件ANSYS，采用瞬态动力学分析方法，模拟了该桥桥面在2种不同震级的地震波下的响应。结果表明：在7.0级的地震作用下，海珠桥桥面的最大位移、最大应力均满足规范要求，而在8.0级地震的作用下，最大应力大于规范要求。因此，对于7级及以下的地震，海珠桥桥面具有可靠的安全性能，而要抵御8级以上的地震，则需要对桥桥面进行加固。

桥梁工程；抗震性能；有限元；地震波

广州海珠桥是中国第一座钢桥和广州市第一座跨江桥梁，由德国工程师设计、美国公司兴建，使用英国钢材，于1933-02正式通车，至今已服役81年。海珠桥虽未受过大型地震的影响，但对其进行抗震安全性评估仍具有非常重要的意义［1-2］。本文以海珠桥桥面为具体研究对象，借助大型有限元软件ANSYS，建立和修正了该桥梁桥面的有限元模型，模拟了其在不同地震波作用下的响应，结合最新相关设计规范资料，评估了桥梁桥面的耐震能力和耐荷能力，为其加固改造提供依据。

1海珠桥概况

广州海珠桥（如图1所示）始建于1933年，全长356.67 m，主桥全长182.90 m，南北两跨对称布置，原为3孔下承式简支钢桁架桥，设计荷载为2列10 t汽车，中跨为开启式结构，能向上分开，以便大船通过。主引桥为钢筋混凝土结构，靠近主桥第1、2跨为钢筋混凝土变高度简支T梁，北岸跨径7.0 m，南岸跨径11.2 m。其它跨为整体式钢筋混凝土简支板，跨径为4.6 m。北引桥19孔，总长91.6 m，南引桥15孔，总长82.2 m。

图1　广州海珠桥

随着经济的发展，为满足日益增长的交通流量需求，1975年对海珠桥进行了扩建，在该桥东、西两侧各拓宽7.83 m，连同原钢桥人行道合为11.24 m的非机动车道和人行道，跨度与主钢桥一致。边桥主桥为双悬臂带挂梁变截面预应力箱梁结构，东西两幅，单向行车，单幅桥面宽11.26 m。边桥北引桥为7孔钢筋混凝土简支T梁桥，南引桥为6孔钢筋混凝土简支T梁桥，跨径9.3 m。东西两幅，单向行车，单幅桥面宽8.4 m。

1995年，广州市市政局组织对海珠桥主桥钢桁架进行维修加固，采用自锚式悬索吊桥加固方案，将中孔恒载转嫁到吊索上，原桥变为3孔连续自锚式悬索吊桥。经体系转换后，主桥设计荷载为汽-15。经扩建的海珠桥，新旧桥既独立又联体，现桥长486 m，正桥182 m，桥宽33 m。

为了考察加固后海珠桥桥面的安全性能，本文对该桥桥面在地震荷载下的动力响应进行研究，以期了解该桥桥面的抗震性能。

2有限元模型的建立和修正

为了模拟海珠桥桥面在地震荷载下的动力响应，依据扩建后海珠桥的图纸，建立了包含桥面板在内的桥梁有限元模型。

2.1初始模型的建立

在海珠桥初始有限元模型中（见图2），共有关键点100 000个，节点57 432个，单元61 749个，其中线单元4 455个，面单元1 336个，没有体单元；共定义了3种单元类型：悬索采用link 8单元，桥面板采用shell 181单元，钢桁架结构采用beam 4单元；此外，还定义44组实常数以及4组材料属性。

图2　海珠桥初始有限元模型

根据文献［3］中的规定，梁体自重为恒载，而桥面铺装、栏杆、设备等重量为二期恒载，这些荷载作为自重荷载施加在海珠桥初始有限元模型上。将海珠桥的车辆荷载等效为中国公路规范Ⅰ级车道荷载的均布荷载，其标准值q =10.5 kN/m，桥面底板与桥墩处采用固定约束，边跨与地基采用铰接支座。通过对密度和重力加速度的定义，来完成桥梁自重的施加。

有限元计算可知桥面的最大应力为183 MPa，低于工程中Q345钢材的屈服强度和许用应力，且桥面整体下沉位移约为5 cm，但桥面两侧人行道的下沉位移较大，最大下沉位移接近47 cm，这样的下沉位移明显是过大的。究其原因，是由于在初始模型中，对两侧人行道同样施加了车荷载，而人行道本来是不加混凝土的，这种不恰当的加载方式导致了人行道下沉位移较大，所以需要对初始模型加以修正。

对比施加自重、车荷载和不施加自重只施加车荷载的情况下，整个桥面的下沉位移和其应力强度，可以发现，桥面板受自重影响显著，因而在修正有限元模型时将考虑对桥面板进行等效研究。

2.2有限元模型的修正

通过有限元方法计算得到的结构响应与实测响应之间会不可避免地存在一定偏差。通过模型修正，可以获得一个接近真实结构的分析模型，这样可以进一步分析结构对偶遇或异常荷载的响应。同时，修正后的有限元模型可以带来更为经济的设计，为结构的维护提供更为准确的分析依据［4］。

初始模型中海珠桥桥面两侧的人行道下沉位移较大，为了简化结构，将人行道板与行车道板的厚度保持一致。通过加大人行道板的刚度，从而提高人行道板的承载能力，即进行桥面板的刚度等效，提高桥面刚度，解决下沉问题。主要步骤如下：

（1）取50 mm的混凝土板和8 mm的钢板，将2个板叠在一起，一起承受荷载。给板施加四边固支的约束，使得板在自重下发生下沉，求解最大下沉位移；

（2）将步骤（1）中2层板的约束变为双边简支，使得板在自重下发生下沉，求解最大下沉位移；

（3）做一40 mm的板，将板四边固支，使得板在自重下发生下沉，调节板的弹性模量，最终使得下沉位移与步骤（1）中的下沉位移达到一致，记录此时板的弹性模量；

（4）将步骤（3）中单层板的约束变为双边简支，并将步骤（3）中得到的弹性模量代入，使得板在自重下发生下沉，将此时的最大下沉位移与步骤（2）中的最大下沉位移进行比较；

（5）在步骤（1）中所建模型上施加海珠桥的设计荷载，在自重和设计荷载作用下，使得板发生下沉，求解后记录最大下沉位移；

（6）同样在步骤（2）中的模型中施加海珠桥的设计荷载，在自重和设计荷载作用下，使得板发生下沉，求解后记录最大下沉位移；

（7）在步骤（3）中所建的单层板模型上施加海珠桥的设计荷载，在自重和设计荷载作用下，使得板发生下沉，调节弹性模量，使得最大下沉位移与（6）中的最大下沉位移达到一致，记录此时板的弹性模量；

（8）将步骤（4）中所建的简支单层板模型中施加海珠桥的设计荷载，将（7）中得到的弹性模量代入，在自重和设计荷载作用下板发生下沉，将最大下沉位移与（6）中的最大下沉位移进行比较。

（9）以上4步为四边固支检验双边简支得到等效弹性模量的步骤，接着进行双边简支检验四边固支得到等效弹性模量。

通过上述步骤可以最终确定海珠桥钢筋混凝土桥面板的等效弹性模量，为后续的模型验证提供准备。

2.3海珠桥静力荷载下的响应

根据上一节中已经求得的海珠桥桥面板的等效弹性模量，将由钢板和混凝土板组成的桥面板等效为一层厚为40 mm钢筋混凝土桥板，以此来进行模型修正。此外，根据前面的计算结果，考虑到两侧人行道的下沉位移过大，定义了一组新的材料属性，从而加大人行道板的刚度。最后，完成对整个修正模型的求解，得到其在静力荷载下的位移和应力响应图，见图3和图4。从图中可以看出，此时人行道在设计荷载下的下沉位移较之修正前有了明显的降低，应力强度亦符合要求。

图3　二次修正模型在设计荷载下的位移图

图4　二次修正模型在设计荷载下的应力强度图

3　地震荷载下海珠桥动力响应模拟

基于修正后的有限元模型，进行地震波下海珠桥的动力响应的模拟与计算。

3.1输入地震波

在结构地震反应时程分析中，合适的地震动加速度时间过程的选取至关重要。然而，由于目前国内外地震观测记录的缺乏，所分析的结构物附近的地震观测记录更难以得到，所以在地震数值计算中一般采用人造地震动。人造地震动有多种途径，主要包括比例法和拟合目标反应谱的数值法［5］。本文采用比例法来进行模拟和分析。

查阅我国主要城镇抗震设防烈度和设计基本加速度可知，海珠桥结构按7度烈度设防，设计基本加速度值为0.1 g，即将加速度峰值调整为0.98 m/s2［6］。考虑到广州软土层分布广泛，场地类别设为3级，因而分析中采用适合三类场地的taft波进行模拟，其震级为7.36级。图5是taft波完整的地震加速度记录曲线。

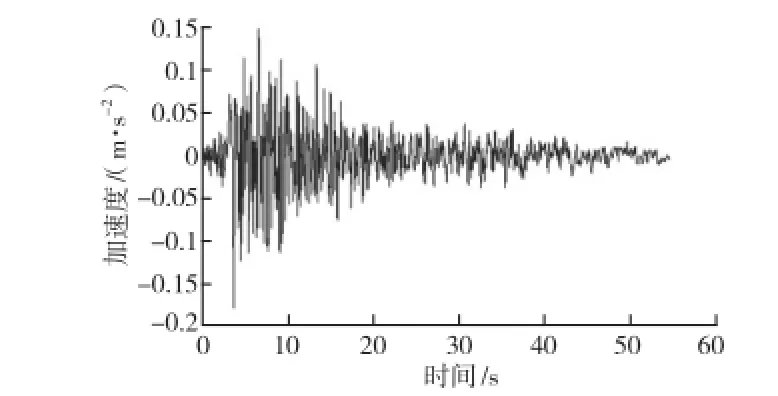
图5　taft地震波加速度记录曲线

通过观察发现，在整个地震过程中，前20 s的能量占据了绝大部分，且峰值也出现在前20 s内，因而我们选取峰值附近，即全过程中的前20 s进行分析计算。将前20 s的加速度曲线按照规定进行规格化处理，如图6所示。

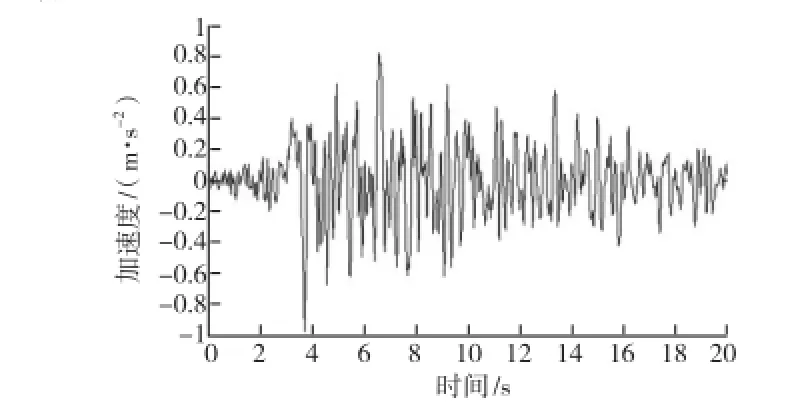
图6　规格化后前20 s加速度曲线

3.2计算结果

计算中时间步长△t取为0.02 s，共计1 000步，总时长为20 s。图7和图8分别是海珠桥桥面板在taft波作用下的Y向位移响应和应力强度图。

图7　taft波作用下Y向位移图

图8 taft波作用下应力强度图

通过拾取位移和应力2幅图中最大值所对应的节点，作出该节点处的位移时程图和应力时程图，如图9和图10所示。

通过对位移图的观察，可以发现，从整体来看，整座桥的主跨位移较小，相对而言边跨位移要大很多。而在边跨中，两侧人行道处的位移较大，最大值约为0.12 m，中间车道处的位移则较小。从应力图来看，亦是边跨的应力大于主跨，边跨中人行道处的应力大于中间车道，最大应力强度达到了200 MPa。根据文献［7］中的规定：结构各部件在多遇地震（设计地震E1）作用下最危险截面的应力不能超过相应材料的许用应力，保证结构在多遇地震作用下，处于弹性范围内工作。

一般钢桥多采用Q345钢材，其许用应力约为230 MPa，即在taft波作用下，应力是满足要求的；Y向最大位移0.12 m也符合要求，因而结构具有可靠的安全性能。

图9　Y向位移-时间图（taft波）

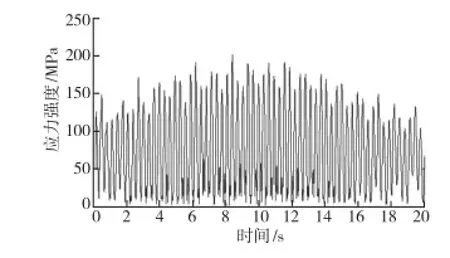
图10　应力强度-时间图（taft波）

3.3taft波后续讨论

采用震级为里氏8.0级，震中烈度最大为11度的汶川地震波［8］进行模拟，来考察海珠桥桥面在8.0级地震下的动力响应和安全性能。汶川大地震是浅源地震，震源深度为10～20 km，因此破坏性巨大［9］。选用加速度最大值附近的前16 s进行模拟，其加速度与时间的关系图如图11所示。

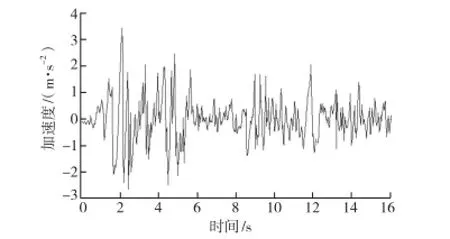
图11　汶川地震波前16 s加速度记录曲线

处理步骤与taft波类似，输入完地震波，待计算结束后，在通用后处理器中，可以得到如图12所示的Y向位移图和图13所示的应力图。

由图12、图13可以发现，在汶川波的作用下，位移与应变图都有明显的变化。在位移图中，桥梁两侧人行道仍具有相对较大的位移，但最大值并非发生在此处，而是位于桥梁的两端，从图14所示的该节点处的位移时程曲线中可以看到，最大值约有0.36 m。在应力图中，桥梁两端也具有相对较大的应力，但最大值却仍是发生在边跨两侧的人行道处，与taft波类似，从图15所示的该节点的应力时程曲线中可以发现，最大值达到了380 MPa，不仅远远超过了一般桥梁用钢材的许用应力，不满足规范要求，也超过了其屈服强度，将发生塑性变形，产生塑性破坏，对桥梁的安全性能产生巨大影响。

图12　汶川波下海珠桥桥面Y向位移图（汶川地震波）

图13　汶川波下海珠桥桥面应力强度分布图

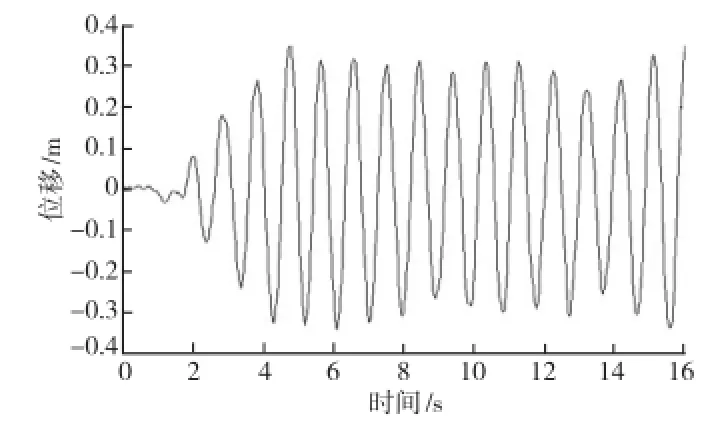
图14　位移最大节点的位移时程图

图15　应力最大节点的应力时程图

4　结论

本文基于有限元软件ANSYS，模拟了海珠桥桥面在不同地震荷载下的响应，验证了桥梁桥面的抗震性能。主要结论如下：

（1）在地震波的作用下，海珠桥边跨两侧的人行道位移和应力均高于其他部位，因而需要对此处进行加固，可以通过布置加劲肋来改善这一问题；

（2）在7级地震作用下，海珠桥桥面结构的强度与刚度均满足规范要求，具有可靠的安全性能；

（3）在8级地震的作用下，桥梁桥面的强度不满足要求，将出现塑性破坏，不具备可靠的安全性能，若要抵御8级地震，则需要对桥梁桥面进行加固。

［1］曹永占.我国已建桥梁的安全性评估方法分析［J］.交通世界，2010（11）：159-160.

［2］冯杰.桥梁结构地震易损性分析研究［D］. 成都：西南交通大学，2010.

［3］JTGD60—2004公路桥涵设计通用规范［S］.

［4］吴晓菊.结构有限元模型修正综述［J］.特种结构，2009 （1）：39-45.

［5］张皎，郭明珠，季杨.简论人造地震动的研究［J］.世界地震工程，2008，24 （3）：159-162.

［6］李杰，艾晓秋.基于物理的随机地震动模型研究［J］.地震工程与工程振动，2007，26（5）：21-26.

［7］JTG/T B02-01—2008公路桥梁抗震设计细则［S］.

［8］LI H，LU M，WEN Z，et al. Characteristics of bridge damages in Wenchuan earthquake［J］. Journal of Nanjing University of Technology （Natural Science Edition），2009（1）：6.

［9］曹俊兴，刘树根.对四川汶川大地震有关问题的思考与初步认识［J］.成都理工大学学报 （自然科学版）， 2008，35 （4）： 414-425.

Response Simulation for Guangzhou Haizhu Bridge Deck under Earthquake Load

Liu Lin， Guo Li， Gao Wenkun
（College of Civil Engineering， Southeast University， Nanjing 210096， China）

To study the safety performance of deck slab of Guangzhou Haizhu bridge， general finite element analysis software ANSYS is used to conduct transient dynamic analysis. Responses of the bridge deck slab under two kinds of earthquake waves are simulated. The results show that the max stress and strain of the deck slab of the bridge meet the stipulations of the Code under the earthquake with Ms 7.0. However， the max strain is over criterion value under the earthquake with Ms 8.0. Therefore， Haizhu bridge deck slab is safe and reliable under magnitude earthquake with Ms 7.0 and needs to be reinforced to withstand earthquake with Ms 7.0.

bridge engineering； anti-seismic performance； FEA； earthquake wave

U442.55

A

1672-9889（2015）01-0026-04

刘麟（1991-），男，江苏常州人，硕士研究生，研究方向为有限元计算模拟、混凝土研究以及结构健康监测。

（2014-06-19）