基于转变矩阵描述的个体阶段性发展：潜在转变模型

王碧瑶 张敏强 张洁婷 胡 俊

（华南师范大学心理学院／心理应用研究中心，广州 510631）

1 前言

纵向研究可以分析个体心理与行为发展变化的一般趋势和个体差异，在发展、社会、教育、临床等心理研究领域有广泛应用［1，2］。以往研究者往往关心总体中某一行为或特质随时间发展的趋势，采用的统计方法主要有重复测量方差分析 （repeated measures analysis of variance，RM ANOVA），多层线性模型（hierarchical linear model，HLM）和潜变量增长曲线模型（latent growth curve model，LGM）等。近年来，随着理论研究和统计方法的快速发展，总体中的个体异质性（heterogeneity）引起了研究者的广泛关注，纵向研究的问题也逐渐由以往的注重总体平均趋势的发展过渡到综合考虑总体平均趋势和个体发展差异的系统分析的问题［3］。

因此，一些个体定向（person－oriented）的纵向数据分析方法应运而生，如潜类别增长曲线模型（latent class growth model，LCGM）、潜变量混合增长模型（growth mixture model，GMM）和潜在转变模型（latent transition analysis，LTA）。这三种方法都能够研究类别型潜变量，其中，潜变量混合增长模型根据个体的发展轨迹（斜率和截距）的特征将其分为不同潜在类别，潜类别增长曲线模型是其控制组内方差为零的一种特殊形式，这两种方法适合于分析具有程度高低、概念化（conceptualized）的行为，如对儿童同伴关系相对地位，可以将其作答转换成标准分数［4］。而潜在转变模型根据作答模式将个体分为不同的潜在类别，并允许个体所属类别随时间的发展发生变化（图1），适合于分析难以描述程度高低、多层面（multifaceted）的行为，如青少年不良行为，可以分为说谎、偷窃、打架等方面［5］。

潜在转变模型是潜在类别分析 （latent class analysis）基础上进行纵向拓展的一种潜马尔科夫模型（latent markov model），适用于分析外显变量和潜在变量都属于类别型的数据。该方法最早由Collins与Wugalter［6］提出，已被应用于许多心理学和社会科学领域的研究，如儿童情绪和认知的成长过程［7，8］，青少年不良行为和心理问题随时间的发展［9，10］，药物滥用和成瘾行为的干预效果［11，12］，临床和心理疾病的追踪治疗［13，14］等诸多方面。

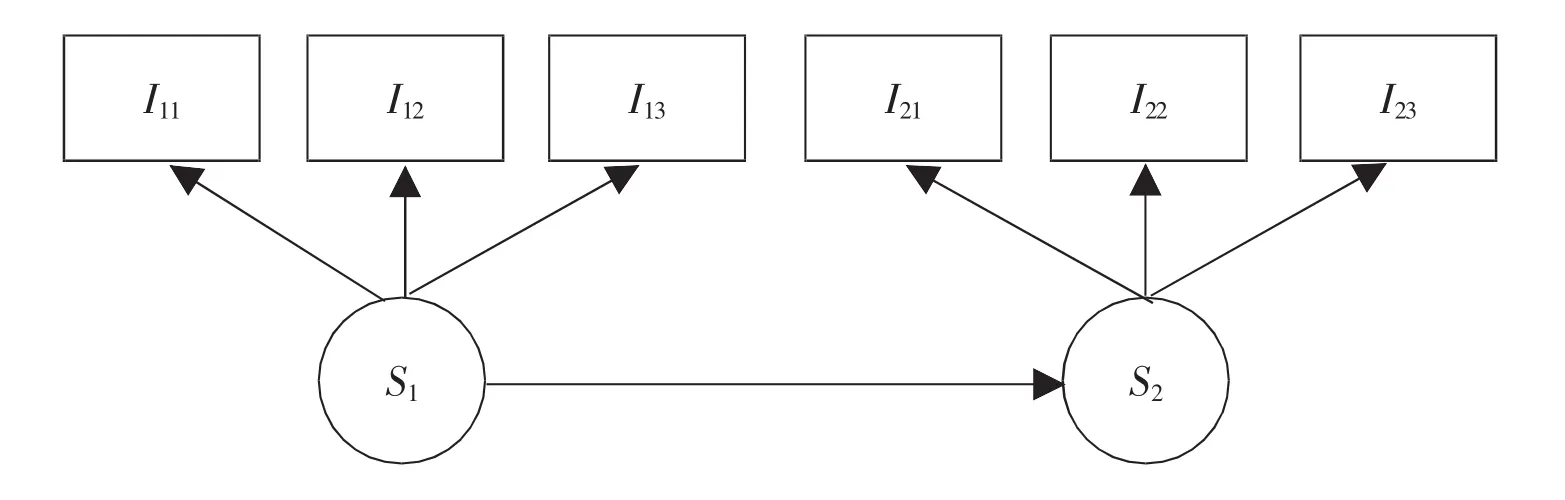
图1 具有三个外显变量、两个时间点的潜在转变模型

潜在转变模型通过转变矩阵，从转变概率的角度来刻画发展，为研究个体的阶段性发展（stage process）提供了一种全新的视角，即以个体所属类别不变的概率来表示该类别的稳定性，以个体转变到其它组的概率来表示其发展趋势。本文对潜在转变模型做了简要介绍，并通过一组青少年冲动行为数据的分析过程为例，说明其具体应用方法及步骤，并讨论了潜在转变模型与其它纵向研究方法相比的优点。

2 潜在转变模型

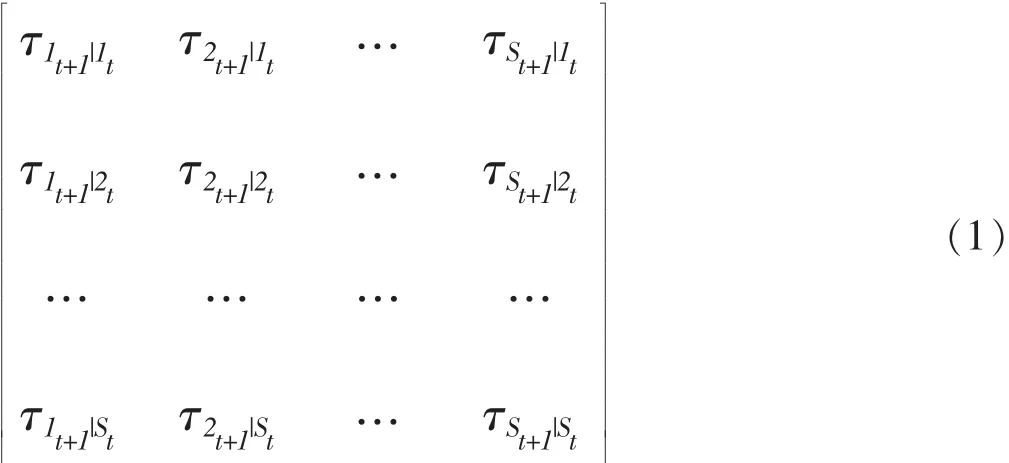
潜在转变模型中估计三种参数：（1）条件概率ρ，即个体对于外显变量的作答概率，类似于IRT中的项目反应概率。由于不同潜在状态对外显变量具有不同的作答特征，因此条件概率反映了潜在状态之间的差异性，也是对其进行解释和命名的依据；（2）转变概率τ，即表示个体在t时间点上属于潜在状态St，在t+1时间点上属于潜在状态St+1的概率，反映了潜在状态随时间的发展。如果有S个潜在状态和T个测量时间点，则共有S（T-1）个转变概率；（3）潜在状态概率δ，表示个体在某个时间点属于某潜在状态的概率，反映了潜在状态占总体的比例。在潜在转变模型中，只需估计T1时间点的潜在状态概率，其它时间的潜在状态概率可以由转变概率计算得出。

任意两个连续时间点间的转变概率都可以用一个S×S矩阵来表示，该矩阵如下公式（1）所示。矩阵的对角线表示的是被试在两个时间点属于同一潜在状态的概率，即没有发生转变的概率。转变概率矩阵每行之和为1，即在时间点t到时间点t+1，个体从某潜在状态向各潜在状态转变的概率之和为1。对于T次测量，共有T-1个转变概率矩阵。

假设有t=1，……，T个时间点，外显变量有j=1，……，J 个，分别有 rj，t=1，……，Rj，t个作答水平，y=（r1，1，……rJ，T）是某被试的作答向量。 在任意时间点上潜在状态L有S种，St=1，……，St表示在时间点t上的潜在状态。最基本的潜在转变模型为：

I（yj，t=rj，t）是 一 个 指 示 函 数 ，用 于 选 择 合 适 的 ρ进入公式（2）。在时间点t，如果被试在外显变量上的作答为 rj，t，I=1，否则 I=0。

潜在转变模型中还可以纳入协变量和分组变量（如，性别），探究影响潜在状态及其转变的因素和组间差异，含有协变量X和分组变量G的潜在转变模型如公式（3）所示：

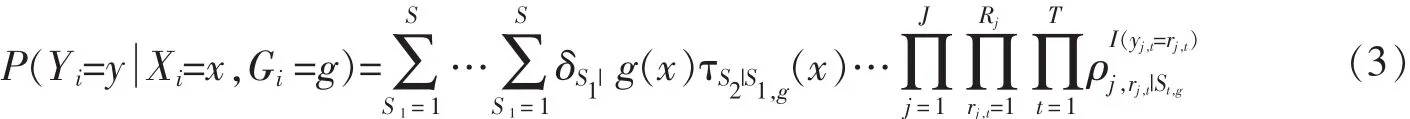
加入协变量后，需要估计一个新的参数Logistic回归系数β，而不再估计转变概率和潜在状态，转变概率τ和潜在状态δ都可以表达为β的函数，如公式（4）和（5）。同时，上述所有参数都同时受到分组变量 G 的影响（δ，τ，ρ，β）。

潜在转变分析的基本过程与潜在类别分析类似，但是要注意以下几点：

（1）在选择最佳模型时，不仅要综合考虑AIC、BIC等模型拟合指标和模型的简洁性，还要通过潜在类别分析检查单个时间点的最佳模型和潜在状态，防止最终的潜在结构及其转变模式可能忽略掉单个时间点的重要信息［5］。

（2）研究者通常限定同一潜在状态在不同时间点的条件概率 ρ1，ρ2，…，ρt保持不变（只有一个条件概率ρ），使潜在转变模型更加简洁和易于解释。这一做法的前提是限定模型通过了一致性检验（measurement invariance），即条件概率参数限定的模型与条件概率自由估计的模型在数据拟合性上不存在显著差异。

（3）潜在转变分析中的协变量分为两种：预测某一时间点潜在状态概率和预测任意两个连续时间点转变概率，这两种协变量对潜在转变模型的影响都可以通过多项Logistic回归来计算目标组与参照组的发生比（odds ratio）。当潜在状态超过3个（包含3个）时，计算协变量对转变概率的影响还可以采用二项Logistic回归来计算，此时的发生比是潜在状态发生转变与保持不变之比。

目前可以进行潜在转变分析的软件有SAS、WinLTA和Mplus，本文采用SAS软件中的PROC LTA程序进行，该程序可以进行包括分组变量和协变量的潜在转变分析，并可以在http：／／methodology．psu．edu．免费下载［15］。

3 应用案例

下面例子采用一批关于青少年冲动行为的纵向数据［16］。 采用青少年冲动行为量表（IBCL－A）［17］对中国香港地区的3600名中学生（M＝14．63，SD＝1．25）的8种冲动行为进行为期一年半的追踪，共进行三次测量，每次时间间隔为六个月，所有作答转变为二分变量“有”或“无”，各种行为的发生率见表1。

比较潜在状态数为2到6的模型发现，在潜在状态达到4以后，模型拟合度随其复杂度的提升不再明显，进一步检验到T1到T3的最佳模型都为四类别模型，一致性检验支持了所有时间点的条件概率相同的假设，本例最终选择了条件限制的四类别潜在转变模型（表2）。

表1 冲动行为的发生率 （N＝3600，其中女性占57%）

根据条件概率（图2），潜在转变模型识别出了四个异质性的子群体：克制组、享受型冲动组、攻击型冲动组和严重冲动组。除了所有组都出现了“因盛怒而向别人大喊”这种程度较轻的冲动行为外，克制组的被试在所有项目上的发生率都很低，享受型冲动组可能出现“不能自制地进食”和“不能自制地消费”，攻击型冲动组在“攻击他人或涉入打架”上具有较高的发生率，而严重冲动组则可能出现多种冲动行为，包括性质较为严重的“发生自我伤害”。

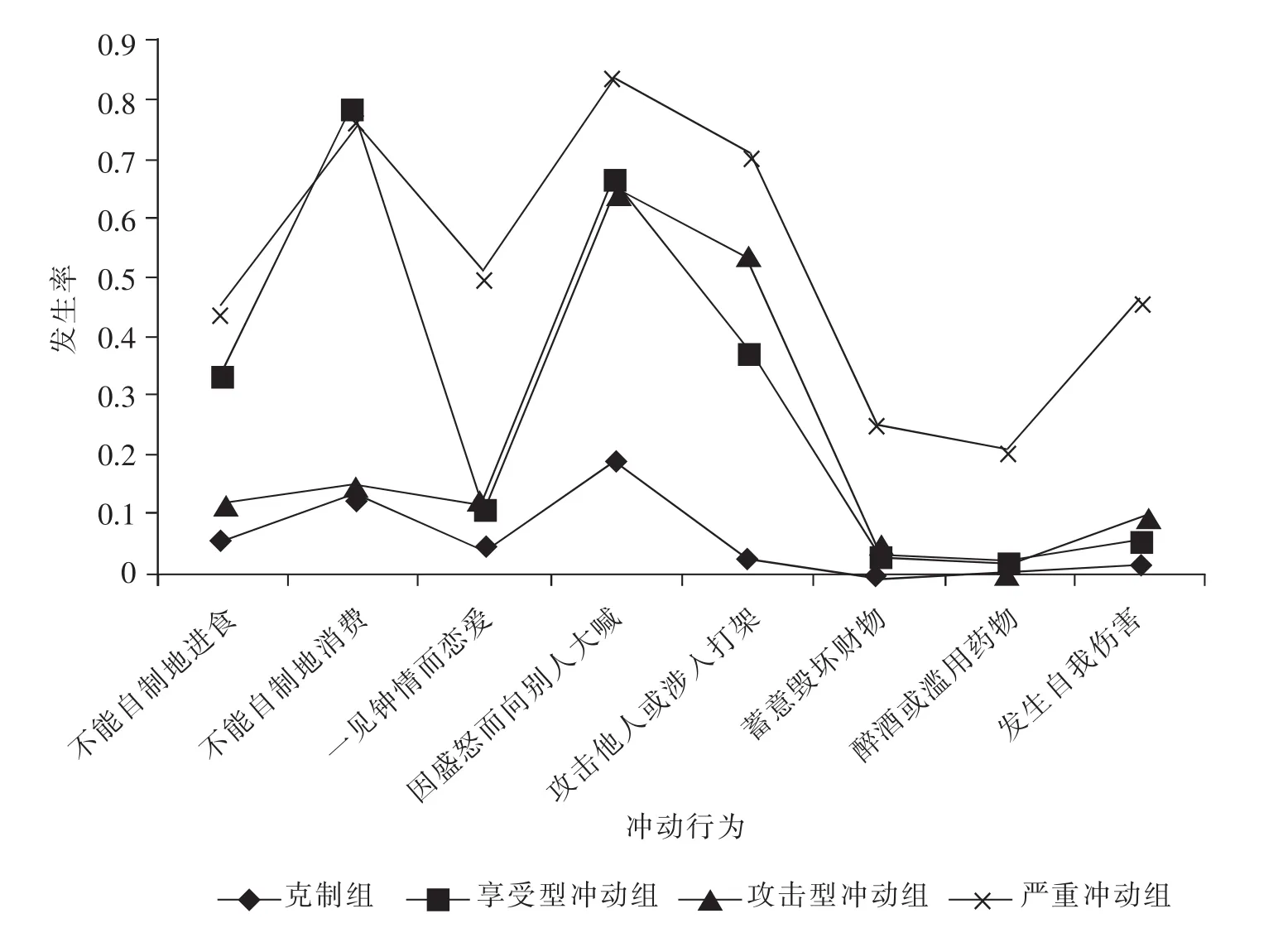
图2 四类别潜在转变模型的条件概率

在三个时间点，克制组占总体的比例都最高，享受型冲动组的比例随时间上升而攻击型冲动组的比例随时间下降，严重冲动组的比例最低且基本稳定（表2）。由潜在转变模型的分类结果可以看出，虽然多数冲动行为的发生率并不高 （一半行为的发生率低于0．20），青少年中属于冲动组（享受型冲动组、攻击型冲动组和严重冲动组）的比例却高达2／3。将性别作为分组变量纳入潜在转变模型后发现 （未在表格中列出），女性比男性更可能属于享受型冲动组且该比例随时间上升的速度更快 （女性从0．31到0．40，男性从 0．12 到 0．17），而男性比女性更可能属于攻击型冲动组且该比例随时间下降得更慢 （女性从 0．21 到 0．12，男性从 0．40 到 0．28）。

潜在转变分析最大的特点之一就是通过转变矩阵解释不同潜在状态的发展，从转变概率的角度描述其稳定性和发展方向。由表2可以看出，在第一次转变中（T1到T2，学生升入高一年级），克制组的被试几乎都保持原组，而享受型冲动组、攻击型冲动组和严重冲动组的部分被试则可能转变到了冲动行为更少的组，即冲动行为减少；在第二次转变中（T2到T3，学生从某学年上学期至下学期），享受型冲动组和严重冲动组的稳定性更强，而克制组和攻击型冲动组的部分被试则可能转变到了冲动行为更多的组，即冲动行为增加。潜在转变分析捕捉到的这一特点为研究冲动行为的发展提供了新思路，在检验了该发展趋势对所有年龄学生都适用后，得出猜想：冲动行为受到学业所处阶段影响。

基于前人研究焦虑与冲动性的高度相关［18］，采用焦虑量表（DASS－A）［19］测量被试 T1 的焦虑状态并作为协变量引入潜在转变模型，通过多项Logistic回归分析其对冲动行为潜在状态概率和转变概率的影响，结果见表3。

焦虑对潜在转变模型具有显著的影响 （G22-G21=461.68，df=3，p<0.0001）。 在潜在状态概率上，享受型冲动组、攻击型冲动组和严重冲动组的发生比均大于1，表明在焦虑的影响下，被试属于冲动组的概率升高，尤其是高焦虑被试属于严重冲动组的概率将是低焦虑被试的近10倍。在转变概率上，焦虑也有相似的影响，高焦虑的被试转变到高冲动组的概率普遍上升，而转变到低冲动组的概率普遍降低。纳入潜在状态和转变概率的协变量可以帮助研究者找到对于冲动行为具有预测作用的因素，可以为预防和干预措施提供有针对性的指导。

表2 四类别潜在转变模型的条件概率和潜在状态概率

表3 焦虑对T1潜在状态概率和T转变概率影响的发生比＊

4 讨论

潜在转变模型兼具了潜在类别模型能够分析类别型潜变量和纵向分析能够解释发展趋势的优点，为纵向研究提供了行之有效的方法。与目前常用的一些纵向数据研究方法相比，潜在转变模型具有很强的适用性。

（1）对于重复测量数据的要求较低。由于许多研究在实际过程中面临的一些问题，有相当部分只测量2次［2］。一般的纵向数据研究方法对数据的重复测量次数要求较高，即使是简单线性增长模型也需要3个时间点以上测量才能进行数据拟合，而潜在转变模型可以对较少的测量时间点（如，2个）进行分析，使研究者有了更大的便利和灵活性。

（2）可以分析类别型数据。潜在转变模型的理论基础是潜在类别模型，能有效挖掘类别变量数据信息，弥补基于因子分析等方法发展出的纵向数据研究方法（如，潜变量增长曲线模型）无法处理类别变量的不足，对心理学质化研究提供科学的依据，与其它研究方法互为补充，可更为全面揭示心理研究的内在本质［20］。

（3）可以分析类别型的潜在变量。潜在转变模型基于在观测数据的基础上产生潜在变量进行分析，不易受到观测变量测量量尺和极端数据的影响。此外，潜在转变模型可以分析类别型的潜在变量，揭示个体所属类别的发展变化，即非连续的阶段—序列发展（stage－sequential development），对于个体心理与行为的研究，特别是预测和控制具有重要的意义。

（4）能够识别个体的不同发展模式。许多理论和实证研究都表明心理与行为的发展存在个体异质性（heterogeneity）。 变量定向（variable－oriented）的纵向数据研究方法往往假设抽取样本所代表的总体具有同质性，揭示从个体身上抽取出来的平均的心理过程或发展模式［4］，而潜在转变模型是一种个体定向的方法，能够鉴别出心理与行为的不同发展模式，揭示发展的个体差异［21，22］。

（5）能够同时分析多个外显变量。许多纵向数据研究方法，如潜变量增长曲线模型、潜类别增长曲线分析和潜增长混合模型都通过增长曲线来描述个体的发展轨迹，外显变量只能有一个，而潜在转变模型在每个时间点都将个体在多个外显变量上的作答分类，通过转变矩阵估计个体所属类别的转变，可以同时对多个外显变量进行分析。

上述特点可以总结为表4。

表4 潜在转变模型与其他纵向数据研究方法的适用性对比

尽管潜在转变模型在纵向研究中应用灵活，限制较少，但是在实际应用中仍需要注意以下问题：①缺失数据的处理。外显变量中如果存在缺失数据，可以采用多重插补［23］进行处理，但是如果在分组变量和协变量上存在缺失数据，目前软件无法进行处理，需要将该被试的所有作答删除；②进行参数限制。在潜在转变分析中，由于对外显变量在不同时间点进行重复测量，获得的列联表通常很大，会导致数据缺稀（样本量与列联表单元格数量之比过小），使模型选择、参数估计和Logistic回归出现困难（因某些作答模式的被试数量为0而不能完成），此问题可以通过程序中的BETA PROR语句来设置的先验分布来解决［24］；③排除标签转换（label switching）。 潜在状态排列的顺序是由初始值决定的，不同的初始值可能产生相同的潜在状态，但是排列的顺序不同，在判定两次分析的结果不同时，应对不同潜在状态的条件概率进行人工检查，排除标签转换导致的潜在状态顺序问题［25］。

5 结语

综观上述，对于研究发展趋势不同质的类别型纵向数据，潜在转变模型不仅能够发现研究对象的不可直接观测的异质子群体，利用潜在状态解释个体之间的差异，还能够通过转变矩阵来动态地估计个体在不同时间点所属类别的变化，从转变概率的角度来描述个体的发展，为纵向研究提供了新的视角。

1 刘红云，张雷．追踪数据分析方法及其应用．北京：教育科学出版社，2005．

2 唐文清，方杰，蒋香梅，张敏强．追踪研究方法在国内心理研究中的应用述评．心理发展与教育，2014，30：216-224．

3 刘红云，孟庆茂．纵向数据分析方法．心理科学进展，2003，11：586-592．

4 刘红云．如何描述发展趋势的差异：潜变量混合增长模型．心理科学进展，2007，15：539-544．

5 Collins L M ＆ Lanza S T．Latent class and latent transition analysis：With applications in the social，behavioral，and health sciences．New Jersey：John Wiley ＆ Sons，2010．

6 Collins L M ＆ Wugalter S E．Latent class models for stage－sequential dynamic latent variables．Multivariate Behavioral Research，1992，27：131-157．

7 Connell A，Bullock B M，Dishion T J，et al．Family intervention effects on co－occurring early childhood behavioral and emotional problems：A latent transition analysis approach．Journal of Abnormal Child Psychology，2008，36：1211-1225．

8 Goldweber A，Bradshaw C P，Goodman K，et al．Examining factors associated with （In） Stability in social information processing among urban school children：a latent transition analytic approach．Journal of Clinical Child ＆ Adolescent Psychology，2011，40：715-729．

9 Dembo R，Wareham J，Poythress N，et al．Psychosocial Functioning Problems Over Time Among High－Risk Youths A Latent Class Transition Analysis．Crime ＆ Delinquency，2008，54：644-670．

10 Reboussin B A，Reboussin D M，Liang K Y，et al．Latent transition modeling of progression of health－risk behavior．Multivariate Behavioral Research，1998，33：457-478．

11 Chung H，Park Y ＆ Lanza S T．Latent transition analysis with covariates：pubertal timing and substance use behaviours in adolescent females．Statistics in Medicine，2005，24：2895-2910．

12 Jackson K M，O＇Neill S E ＆ Sher K J．Characterizing alcohol dependence：T ransitions during young and middle adulthood． Experimental and Clinical Psychopharmacology，2006，14：228-244．

13 Castellini G，Fioravanti G，Lo Sauro C，et al．Latent profile and latent transition analyses of eating disorder phenotypes in a clinical sample：A 6－year follow－up study．Psychiatry Research，2013，207：92-99．

14 La Flair L N，Reboussin B A，Storr C L，et al．Childhood abuse and neglect and transitions in stages of alcohol involvement among women：A latent transition analysis approach．Drug and Alcohol Dependence，2013，132：491-498．

15 Lanza S T，Dziak J J，Huang L，et al．PROC LCA＆ PROC LTA User’s Guide （Version 1．3．1）．Methodology Center，Penn State University，University Park，PA，2014．

16 Leung S ＆ Leung F．Construct validity and prevalence rate of borderline personality disorder among Chinese adolescents．Journal of Personality Disorders，2009，23：494-531．

17 You J，Leung F，Lai C M，et al．An Item Response Theory Analysis of the Impulsive Behaviors Checklist for Adolescents．Assessment，2001，18：464-475．

18 Taylor C T，Hirshfeld－Becker D R，Ostacher M J，et al．Anxiety is associated with impulsivity in bipolar disorder．Journal of Anxiety Disorders，2008，22：868-876．

19 Taouk M，Lovibond P ＆ Laube R．Psychometric Properties of a Chinese Version of the 21－item Depression Anxiety Stress Scales （DASS21）．Sydney：Cumberland Hospital，2001．

20 张洁婷，焦璨，张敏强．潜在类别分析技术在心理学研究中的应用．心理科学进展，2010，18：1991-1998．

21 纪林芹，张文新．发展心理学研究中个体定向的理论与方法．心理科学进展，2011，19：1563-1571．

22 Muthén B ＆ Muthén L K．Integrating person－centered and variable －centered analyses：Growth mixture modeling with latent trajectory classes．Alcoholism：Clinical and Experimental Research，2000，24：882-891．

23 Schafer J L．Analysis of Incomplete Multivariate Data．Florida：CRC press，1997．

24 Clogg C C，Rubin D B，Schenker N，et al．Multiple imputation of industry and occupation codes in census public－use samples using Bayesian logistic regression．Journal of the American Statistical Association，1991，86：68-78．

25 Chung H，Loken E ＆ Schafer J L．Difficulties in drawing inferences with finite －mixture models．The American Statistician，2004，58：152-158．