基于代理模型的集成上层建筑开口群角隅应力分析

张峰，何书韬，刘均，程远胜

基于代理模型的集成上层建筑开口群角隅应力分析

张峰1，何书韬2，刘均1，程远胜1

1华中科技大学船舶与海洋工程学院，湖北武汉430074
2中国舰船研究设计中心，湖北武汉430064

针对具有开口群的船舶集成上层建筑，使用ANSYS分析其开口区域的强度特性。在多方案有限元计算的基础上，提出兼顾计算精度和计算成本的强度计算模型。基于该模型，以影响开口区域应力的主要设计参数为设计变量，构造了快速预报开口群角隅节点应力的4种代理模型，并对这4种代理模型进行误差检验，得出在所选取的样本点比例下，Kriging代理模型拟合精度较高。因此，采用构造的Kriging模型分析了结构尺寸对开口角隅节点应力的影响。结果表明：开口面板厚度的变化对角隅节点应力水平影响最大。

船舶集成上层建筑；开口群；简化计算模型；代理模型

期刊网址：www.ship-research.com

引用格式：张峰，何书韬，刘均，等.基于代理模型的集成上层建筑开口群角隅应力分析［J］.中国舰船研究，2015，10（5）：41-46.

ZHANG Feng，HE Shutao，LIU Jun，et al.Stress analysis of the opening area of the ship integrated superstructure based on surrogatemodels［J］.Chinese Journal of Ship Research，2015，10（5）：41-46.

0　引言

隐身技术是提高水面舰船生存能力、作战能力的最有效手段之一［1］。但是，目前多数水面舰船的舰载雷达、通信系统天线林立，极大影响了舰船的隐身性能。集成上层建筑技术有力地解决了舰船隐身性能与通信系统、雷达系统布置之间的矛盾。集成上层建筑技术，是将一体化的射频系统（雷达系统、电子战系统、通信系统）镶嵌在上层建筑壁上，完成射频系统与船舶上层建筑综合集成共外形于一体［2］。集成上层建筑壁上存在布置射频系统的开口群，这些开口群降低了结构的刚度，并且存在应力集中问题。因此，研究含开口群的船舶集成上层建筑强度特性十分重要。杜国和等［3］使用有限元程序计算了船舶艏部上层建筑及侧壁开口群加强结构的强度和振动特性。王龙侃等［4］研究了在惯性力载荷、飞溅载荷下集成上层建筑开口群结构的振动特性。朱锡等［5］对侧壁开口上层建筑的船体立体分段钢质模型进行了弯曲试验，得到了上层建筑结构参与船体总纵弯曲时的应力分布。何祖平等［6］采用有限元法，计算了上层建筑端部和舷侧开口处的应力集中系数，有限元结果与试验吻合较好，验证了该有限元方法的正确性。

另一方面，代理模型技术作为处理复杂系统输入参数与响应之间近似关系的一种方法，其计算量较小，适合工程方案的快速估算和优化设计，已广泛应用于船舶、航空航天等领域。郑少平等［7］基于Kriging方法构造了船舶双层底板架强度和稳定性的计算代理模型，讨论了低样本点比例下Kriging模型代替有限元计算分析的适用性。苟鹏等［8］对响应面、Kriging和径向基神经网络这3种代理模型进行了比较，研究结果表明：Kriging方法具有更高的准确性和稳定性，比其他方法更加适合船舶结构的多学科设计与优化。陈静等［9］使用Kriging模型对船舶典型双层底板架强度和稳定性进行全局敏度分析，得出此方法能够方便、迅速地获得结构在新设计点处的响应指标。Prebeg等［10］基于代理模型技术进行船舶结构的优化设计，得出代理模型技术不仅拥有相当的精度，而且提高了计算收敛稳定性和最终的设计质量。

本文将以某集成上层建筑为研究对象，通过有限元多方案仿真分析，得到兼顾计算精度和计算成本的强度计算模型，然后以该强度计算模型为基础，构造4种预报开口群角隅应力的代理模型，并检验代理模型的精度，最后基于代理模型分析相关结构尺寸变化对角隅应力的影响。

1　上层建筑开口群角隅应力分析有限元模型

1.1上层建筑开口群角隅应力计算模型

图1中的模型A为集成上层建筑完整结构模型。8个开口左右对称布置于斜前壁。采用ANSYS建立有限元模型时，侧壁、甲板等板材采用SHELL181单元模拟，甲板纵桁、舱壁扶强材等骨材采用BEAM188单元模拟。考虑到开口角隅区域存在应力集中，在此区域进行网格加密并检查网格收敛性，最终确定开口角隅区域网格尺寸为50mm。

在集成上层建筑的强度计算中，开口区域的应力是关注的一个方面，从保证计算精度的角度出发，建立完整的上层建筑模型必然可以获得较高的精度，但如此一来，势必大幅增加建模的工作量，增加计算成本，尤其在构建代理模型时需要计算大量的样本点方案，要花费更多计算时间，因此需要找出一种兼顾计算精度和计算成本的有限元模型。

本文在该上层建筑的强度计算中，采用了3种有限元计算模型：

1）全三维基准模型（模型A）：包含完整的上层建筑结构，高度方向包括全部6层甲板，共5层上层建筑。模型端部及01甲板边线处理为简支。

2）沿船长方向取部分三维模型（模型B）：取模型A从横舱壁（靠近上层建筑后端）到上层建筑前缘范围内的部分模型。01甲板边线及模型端部处理为简支。

3）开口群所在平面板架模型（模型C）：取模型A中开口群所在的平面板架，平面板架的边线处理为简支，在该板架与各层甲板的交线处约束沿甲板平面方向的位移。

计算载荷考虑飞溅浪花的砰击作用以及船舶摇摆产生的射频设备惯性载荷，其中，通过在上层建筑正前壁、斜前壁、侧壁上施加面压模拟飞溅浪花的砰击作用；在8个开口边线处施加等效节点力模拟射频设备的惯性载荷。

3种计算模型如图1所示。

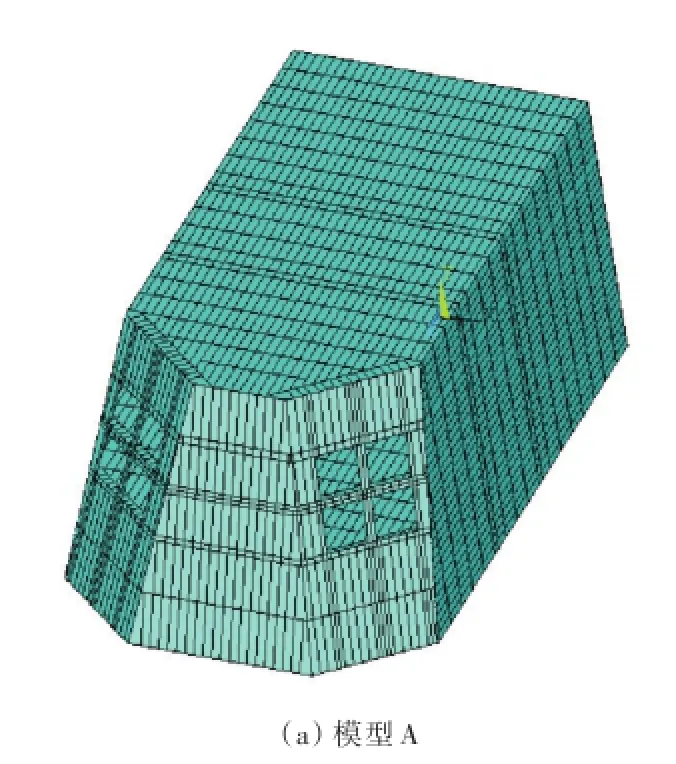
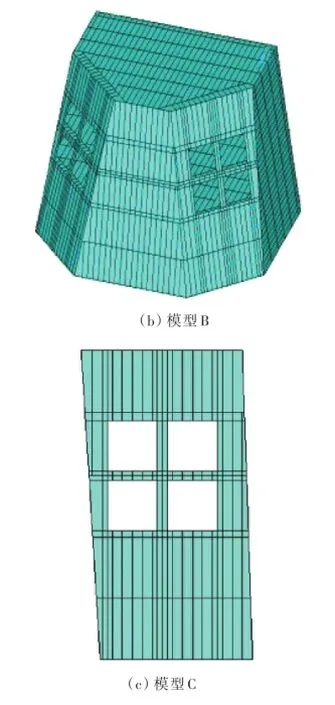
图1　3种有限元计算模型Fig.1　Three FEMmodels

1.2计算结果及分析

采用ANSYS对上述3种有限元模型进行计算，比较各模型在相同载荷条件下计算所得的特征点应力值。本文选择开口角隅区域节点（合计16个）作为特征点，具体分布如图2所示。

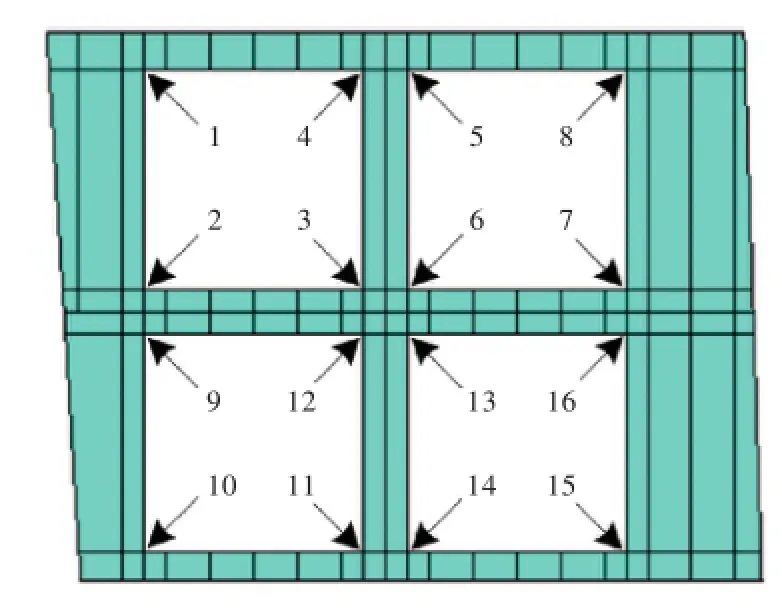
图2　特征点位置分布Fig.2　Distribution of feature points

3种模型开口角隅节点Mises应力如表1所示，应力均为相对值。模型C在特征点的应力值与模型A差距明显，最大相对误差达到194%，平均相对误差达到60.6%，而模型B在特征点的应力水平与模型A十分接近，最大相对误差为12%，平均相对误差仅为4.25%，精度相对较高，因此模型B兼顾了计算精度与计算成本，适合作为构造代理模型的有限元计算模型。

2　上层建筑开口群角隅应力计算代理模型的构造及分析

2.1含开口群集成上层建筑强度计算代理模型的构造

目前，代理模型技术被广泛应用于各工程领域。较常用的有4类代理模型：多项式响应面模型、径向基函数、Kriging模型和神经网络代理模型［7-9］。

基于这4类模型，本节构造了用于快速预报集成上层建筑开口群角隅处应力的代理模型。步骤如下：

1）使用某种试验设计方法产生设计变量的样本点。

2）选择合适的有限元软件分析这些样本点，得到一组响应值。

3）采用某类拟合方法来拟合上述样本点和响应值的输入/输出关系，构造代理模型。

4）检验和评价所构造的代理模型的拟合精度，并利用该代理模型预测新的设计点。

本文使用正交设计方法生成样本点：根据正交性从设计变量取值范围中选择部分具代表性的点作为样本点来代表全部设计点。正交表是实现正交设计的工具，一般形式为 Ln（lk），其中：L为正交表；n为表中行数，即试验次数（样本点总数）；l为每个因素（设计变量）取的水平数（设计变量的取值个数）；k为表中列数，即至多可安排的因素个数。

正交表具有搭配均衡，分布整齐的性质，从而保证了所选样本点的代表性好。

代理模型的设计变量：开口区域面板的厚度、开口四周加强梁的尺寸以及开口区域中心桁材的尺寸。其具体定义及各设计变量的取值空间如表2所示。其中，面板中心桁材即开口群所在板架正中心的桁材。选择开口区域角隅处的Mises应力作为响应值，一组样本点对应16个响应值，记为 yi（i=1，…，16），即图2中第i个特征点在某组样本点下的响应值。

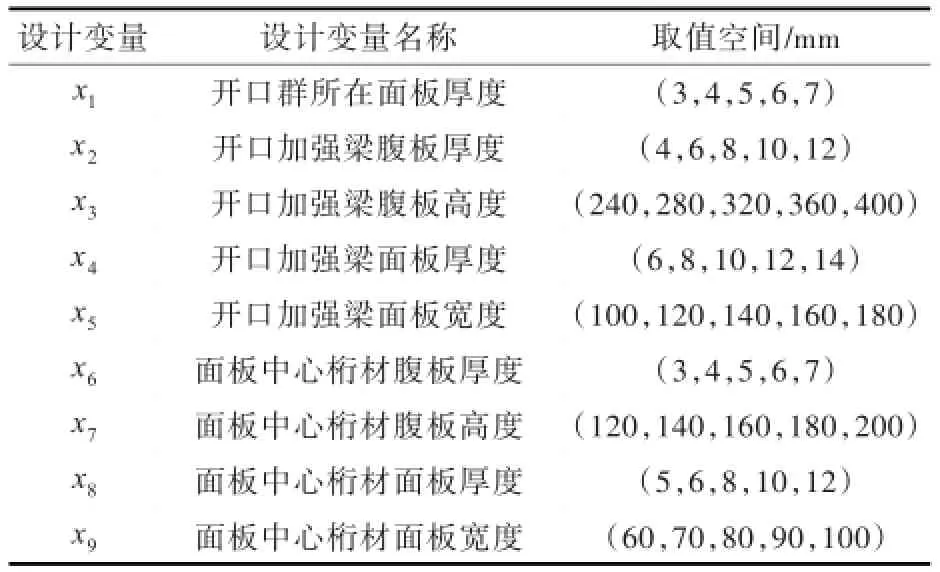
表2　代理模型的设计变量Tab.2　Design variab le of surrogatem odel

本文采用正交设计方法产生样本点，以上每个设计变量取5水平，取54=625个样本点。设计变量取值空间内共有59=1.953 125×106个设计点，所取样本点占样本点总数的比例为3.2×10-4，比例较小。

生成样本点后，采用ANSYSAPDL语言编写模型B的参数化模型、计算命令流程序，该程序实现自动读取样本点数据、建立有限元模型、计算并保存结果。利用该程序计算625个样本点对应的响应值，按前述步骤构建相应的4种代理模型。

根据4种代理模型的数学原理，首先在Matlab软件中编写4种代理模型的实现程序。该程序通过读取样本点及对应的响应值构造并训练相应的代理模型。训练完成后，选取一系列典型的检验点。然后，利用代理模型给出这些检验点的预测值，并采用ANSYS计算检验点的响应值，比较代理模型预测值和有限元计算值，进行误差检验，选择相对误差最小的代理模型。代理模型完整的构造及检验过程如图3所示。

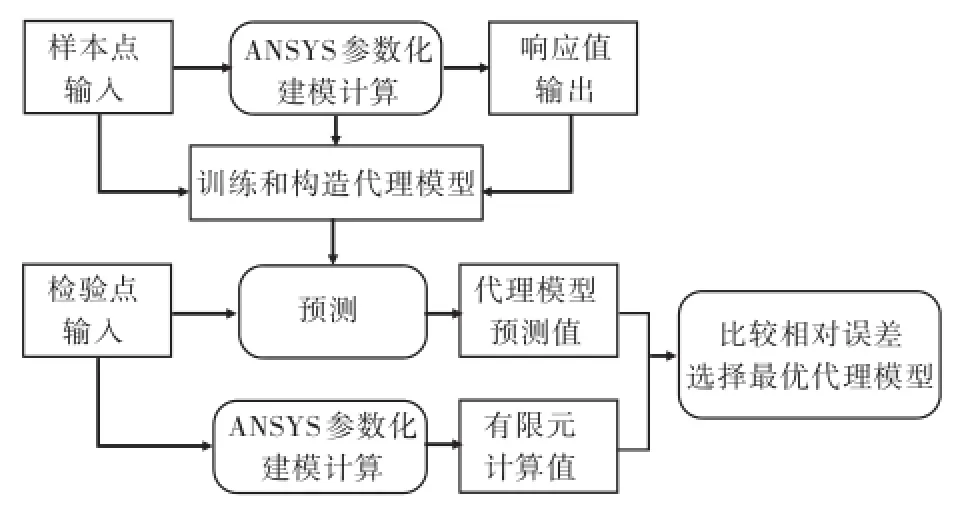
图3　代理模型构造及检验流程图Fig.3　Flow chartof construction and error testof surrogatemodel

2.2代理模型精度检验

以相对误差作为检验标准

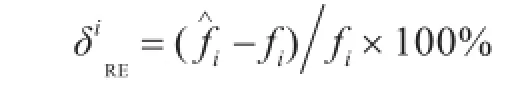
式中：fi为第i个检验点的有限元计算值；为代理模型的预测值；为第i个检验点预测值与计算值的相对误差。

为了便于观察4种代理模型的拟合精度，以10号特征点为代表（其他点类似），将4种代理模型的相对误差绘成直方图（图4）。相比之下，K riging代理模型相对误差最小，分布于-3%～3.5%，且主要集中在-0.5%～3%；响应面代理模型精度最低，相对误差集中在-10%～10%；径向基函数和神经网络代理模型的相对误差处于前两者中间，因此，最终选择Kriging代理模型作为上层建筑开口群角隅应力的预测模型。

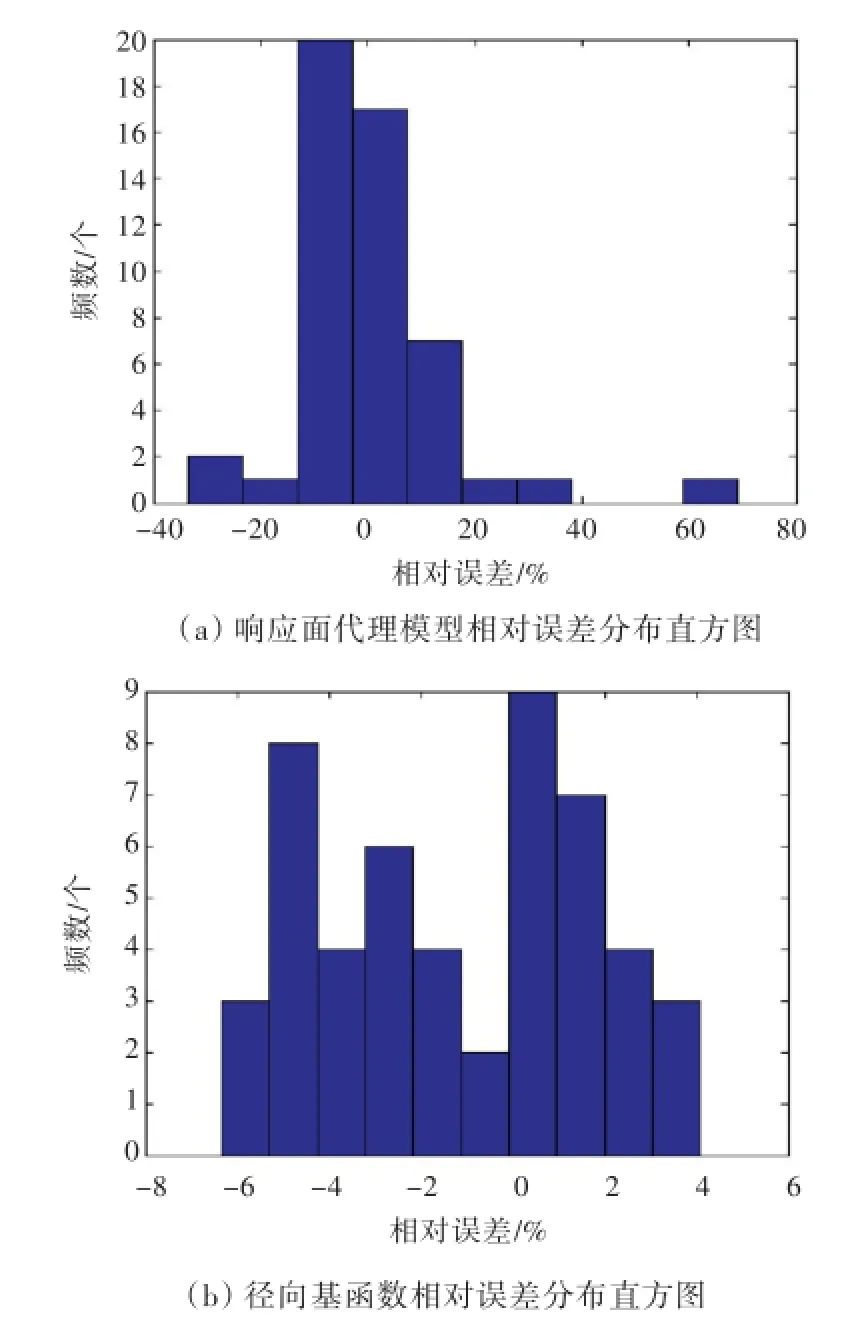
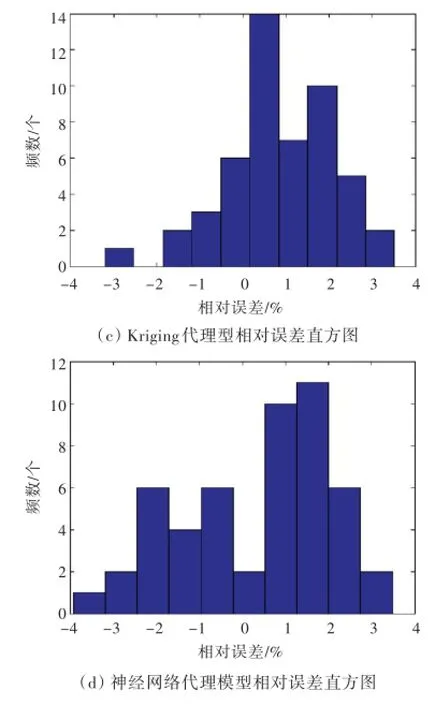
图4　4种代理模型相对误差分布直方图Fig.4　Histograms of relative error distribution of four surrogatemodels

2.3基于代理模型的上层建筑开口群角隅应力分析

为了研究相关尺寸参数对开口角隅处应力的影响，表3给出了结构尺寸的变化方案，并基于上节构造的Kriging代理模型计算开口区域角隅处的应力。原始方案中，开口区域面板厚度为4 mm，开口加强梁尺寸为8×320/10×140，面板中心桁材尺寸为5×160/8×80。在进行参数影响分析时，每次只改变1个参数，另外2个参数保持不变（即原始方案）。以10号和4号特征点为例，给出了应力值随相应尺寸变化的曲线（图5～图6）。从图5中可以明显地看出，影响10号特征点应力水平的因素按重要程度排序为：开口区域面板厚度＞开口加强梁尺寸＞开口区域中心桁材尺寸。当开口区域面板厚度从3，4变化到5mm的过程中，10号特征点应力依次下降了25.6%和22.2%；当开口加强梁从尺寸1依次变化到尺寸4的过程中，相应节点应力依次下降了4.6%，3.3%和5.8%，影响程度较小；当开口加强梁从尺寸4变化到尺寸8时，相应节点应力下降趋势减缓，影响程度进一步减小。而开口区域中心桁材尺寸的改变对10号特征点应力的影响基本可以忽略，这是因为中心桁材距10号特征点较远，其尺寸变化对其应力影响有限。图6为4号特征点应力随结构尺寸变化的曲线。从图6中可以看出，开口区域面板厚度对角隅节点应力影响程度较大，与图5中不同的是，开口区域中心桁材尺寸的变化对4号特征点应力的影响程度增大，造成这一变化的原因是4号与10号特征点位置不同，开口区域中心桁材距离4号特征点更近。

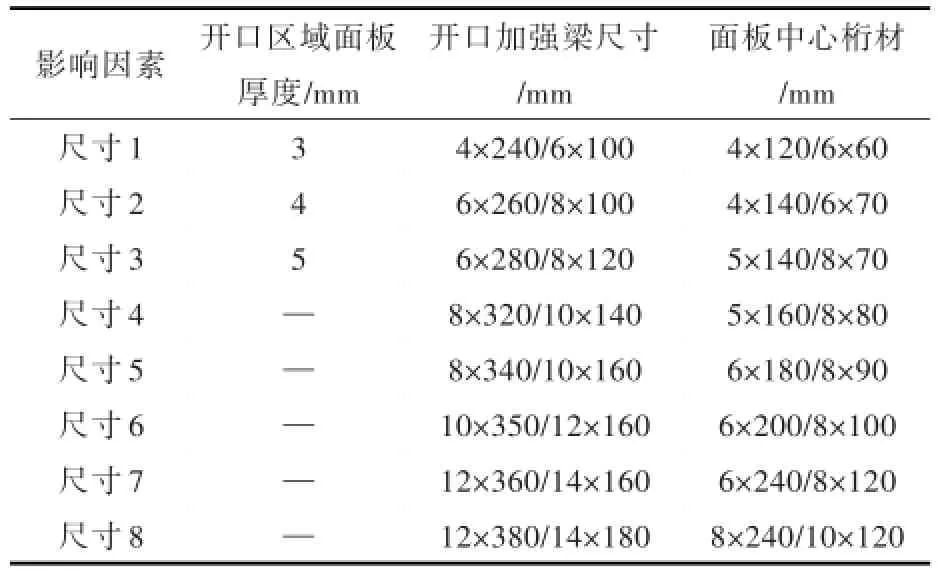
表3　结构尺寸变化方案Tab.3　Changesof structure size

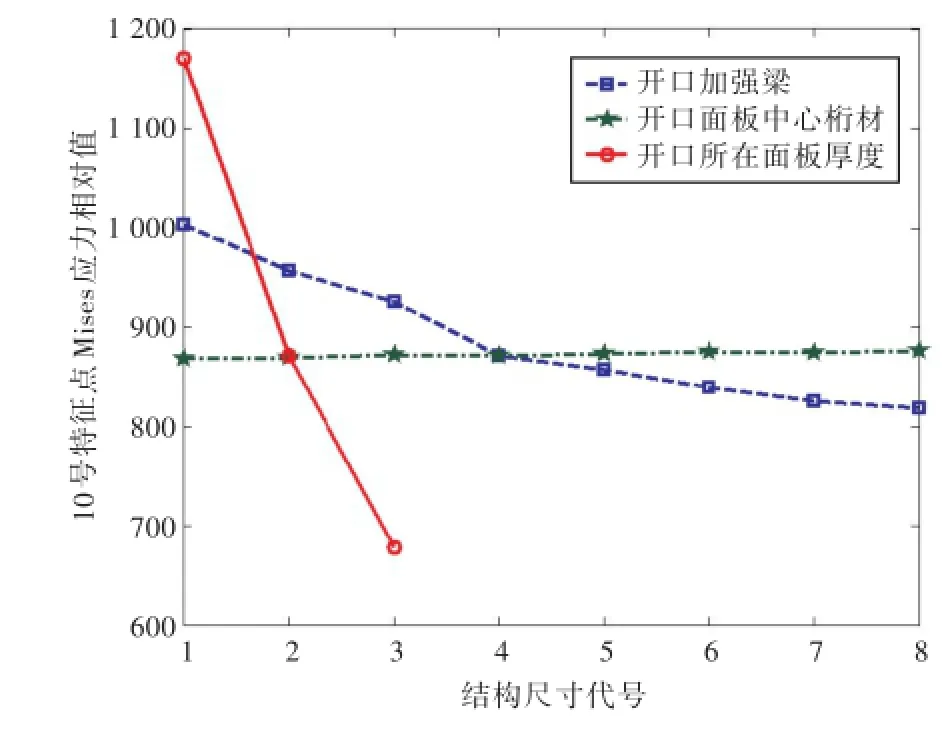
图5　10号特征点Mises应力随结构尺寸变化曲线Fig.5　The trend curvesofMises stresswith the change of structure size at feature point10

图6　4号特征点Mises应力随结构尺寸变化曲线Fig.6　The trend curvesofMises stresswith the change of structure size at feature point4

3　结论

本文以某集成上层建筑为研究对象，通过有限元分析确定了该集成上层建筑强度计算的有限元模型，并基于此模型构造了上层建筑开口区域角隅应力预测的代理模型，基于代理模型讨论了板架主要设计参数对开口角隅应力的影响，得到以下结论：

1）对含开口群的集成上层建筑进行角隅应力分析时，沿长度方向对模型进行适当简化处理（模型B），可以在保证计算精度的同时有效降低计算成本。

2）在样本点比例较低（3.2×10-4）的情况下，Kriging代理模型在4类代理模型中具有最高的精度（相对误差5%以内），适合作为快速预报开口区域角隅应力水平的简化计算方法。

3）结构参数对开口区域应力影响研究表明，开口区域面板的厚度对开口角隅应力影响较大，开口处加强筋尺寸影响次之，而开口区域中心桁材的尺寸对距离其较近的角隅应力有一定影响，对于远离该桁材的角隅应力基本无影响。

［1］ 田斌斌，徐青，罗彩蓉，等.集成式上层建筑对舰船平台设计影响综述［J］.中国舰船研究，2013，8（5）：6-12.

TIAN Binbin，XU Qing，LUO Cairong，et al.An overview of effects of integrated superstructure on p latform design［J］.Chinese Journal of Ship Research，2013，8（5）：6-12.

［2］潘镜芙.水面舰艇上层建筑和桅杆射频综合集成的思考［J］.舰船科学技术，2012，34（5）：3-6.

PAN Jingfu.Topside and mast comp rehensive integration of RF in surface warships［J］.Ship Science and Technology，2012，34（5）：3-6.

［3］ 杜国和，华煜群，姚有顺，等.上层建筑内安装大型设备后结构的强度和振动研究［J］.舰船科学技术，1997（5）：27-29，36.

［4］ 王龙侃，祝祥刚，陈舸，等.集成上层建筑开口群力学性能分析［J］.计算机辅助工程，2013，22（增刊2）：274-279.

WANG Longkan，ZHU Xianggang，CHEN Ge，et al. Mechanical properties of opening group of integrated superstructure［J］.Computer AidedEngineering，2013，22（Supp 2）：274-279.

［5］ 朱锡，张立军，张振华，等.船楼端部侧壁开口对其参与总纵弯曲影响实验研究［J］.中国造船，2003，44（3）：65-73.

ZHU Xi，ZHANG Lijun，ZHANG Zhenhua，et al.Experimental study on effect of cut-apart side wall p late on ship gross longitudinal bending［J］.Shipbuilding of China，2003，44（3）：65-73.

［6］何祖平，王福花，王德禹.舰船上层建筑端部及舷侧大开口应力集中分析和光弹性实验［J］.中国造船，2006，47（1）：84-89.

HE Zuping，WANG Fuhua，WANG Deyu.Analysis and photoelastic test on the stress concentration of superstructure end and broadside with large opening［J］. Shipbuilding of China，2006，47（1）：84-89.

［7］ 郑少平，陈静，程远胜，等.代理模型技术及其在船舶板架强度和稳定性计算中的应用［J］.中国造船，2013，54（1）：40-51.

ZHENG Shaoping，CHEN Jing，CHENG Yuansheng，et al.Surrogatemodels and their application in calculation of strength and stability of ship grillage［J］.Shipbuilding of China，2013，54（1）：40-51.

［8］ 苟鹏，崔维成.基于Kriging模型的深潜器多球交接耐压壳结构优化［J］.船舶力学，2009，13（1）：100-106.

GOU Peng，CUIWeicheng.Structural optim ization of mu ltip le intersecting spherical pressure hu lls based on Krigingmodel［J］.Journal of Ship Mechanics，2009，13（1）：100-106.

［9］ 陈静，詹大为，刘江鹓，等.基于Kriging模型的船舶典型双层底板架强度和稳定性全局敏度分析［J］.中国舰船研究，2014，9（1）：72-80.

CHEN Jing，ZHAN Dawei，LIU Jiangyuan，etal.Kriging model-based global sensitivity analysis of strength and stability for ship grillages［J］.Chinese Journal of Ship Research，2014，9（1）：72-80.

［10］PREBEG P，ZANIC V，VAZIC B.App lication of a surrogate modeling to the ship structural design［J］. Ocean Engineering，2014，84（2）：259-272.

［责任编辑：胡文莉］

Stressanalysisof the opening area of the ship integrated superstructure based on surrogatemodels

ZHANGFeng1，HE Shutao2，LIU Jun1，CHENGYuansheng1
1 Schoolof Naval Architecture and Ocean Engineering，Huazhong University of Science and Technology，Wuhan 430074，China 2 China Ship Developmentand Design Center，Wuhan 430064，China

The strength of the opening area of a ship integrated superstructure is investigated in this paper by using the ANSYS software.A sim plified FEM model considering both simu lation accuracy and computational expense is developed based on the comparison between the results of several FEM models.Based on this simp lified FEM model，four kinds of surrogate models that are used to efficiently predict the corner stress of the opening area of the integrated superstructure are constructed.Meanwhile，error tests of these four surrogatemodels are carried out，and the results indicate that Krigingmodel performs best in terms of fitting accuracy among the four models.Finally，the influences of three differentmajor structure sizes on the stress of the opening area is discussed，where it is concluded that the thickness of the p late has the greatesteffecton the corner stress of the opening area.

integrated ship superstructure；opening group；simplified calculationmode；surrogatemodel

U663.6

ADOI：10.3969/j.issn.1673-3185.2015.05.007

2015-03-12网络出版时间：2015-10-8 11∶10

张峰，男，1990年生，硕士生。研究方向：结构分析与优化。E-mail：zhang123feng@hust.edu.cn

程远胜（通信作者），男，1962年生，博士，教授，博士生导师。研究方向：结构分析与优化，结构冲击动力学与防

护设计，结构振动与噪声控制。E-mail：yscheng@hust.edu.cn

网络出版地址：http∶//www.cnki.net/kcms/detail/42.1755.TJ.20151008.1110.018.htm l