湿蒸汽非平衡凝结流动的热力学特性

韩中合，韩旭，李鹏

（华北电力大学电站设备状态监测与控制教育部重点实验室，河北 保定 071003）

引言

跨声速非平衡凝结流动广泛存在于航空、化工、动力、制冷等工程领域，在动力推进、气液分离、旋转机械节能等方面有着较高的应用价值。核电汽轮机全部级都处于湿蒸汽区，末级出口湿度可达13%，叶片在长期水蚀作用下振动特性改变，出现疏松的蜂窝状组织和应力集中现象[1-3]。这些问题推动了学者们对跨声速非平衡凝结流动机理和相变理论的深入研究。

过饱和蒸汽在通过弯曲通道时不断膨胀，表现出强烈的多维效应和边界效应，同时水滴成核过程中释放出的凝结潜热对跨声速流动起到加热作用。这些特点导致非平衡凝结流动与理想气体等熵流动有很大区别，特别是出现了类似激波的凝结冲波[4-5]。凝结冲波与边界层、激波、尾迹等相互耦合，从而引发了学者们的研究兴趣。由于非平衡凝结相变过程十分复杂，传热传质在微米级水平发生。目前，其描述和计算都是基于半经验公式，很少考虑两相间传热温差以及耦合问题。

本文在湿蒸汽凝结理论和传热传质机理的基础上，对经典成核率进行修正，以提高计算精度；引入了描述水滴生长速率的热质平衡耦合模型，揭示了水蒸气非平衡凝结过程产生的激波现象。讨论了入口压力、过冷度对凝结特性的影响。分析了跨声速流动凝结特性随过冷度的变化规律，得出进口过冷度对凝结位置、激波形态、热力学参数的影响规律。

1 凝结流动数值模型

1.1 输运方程

考虑到水蒸气快速膨胀会出现非平衡凝结相变，大量的小水滴弥散在气相中，其过冷度一般可达30～40 K。由于相变出现，水滴和蒸汽间存在强烈的传热传质过程。基于气液两相的质量、动量、能量守恒以及液相质量分数的输运方程，建立了凝结流动数值模型。Laval喷管稳定流动实验表明，数值计算结果对边界条件相当敏感，在汽轮机非平衡流动中也存在类似现象[6-8]。

水滴半径是凝结流动的重要参数，多数流动模型计算时一般使用平均半径近似求解。Hill[9]通过水滴尺寸分布模型，获得了高精度的水滴半径分布。本文水滴尺寸分布函数由零阶、一阶、二阶矩函数组成。3个函数分别为

平均水滴半径为

整个系统的输运方程为

其中

若系统是封闭的，根据理想气体假设

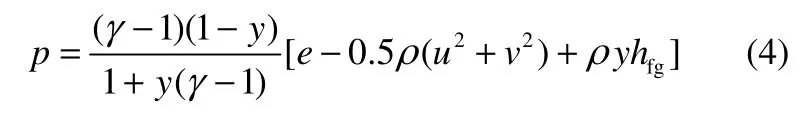
如果液相消失(即x=Q0=Q1=Q2=0)，那么系统将变为单向流动的二维的欧拉方程。

1.2 表面张力修正

单位体积中的经典成核率为

式中，θ3出现在成核率计算式的指数项，其微小变化足以对成核率产生很大影响。图1给出了蒸汽温度与成核率的关系。由图1可知，θ相同时，成核率随温度升高而增加；不同温度下，成核率曲线变化趋势基本相同；但在大张力区域，成核率曲线的斜率越大，此时的计算精度越不易保证。文献中表面张力修正一般采用以下2种方法[10]。

（1）Tolman模型考虑到r对σ的影响，得出修正模型

（2）Kashchiev模型考虑到等温凝结、等压凝结等情况，将Gibbs理论进行整理，在理想气体状态下，推导出修正模型

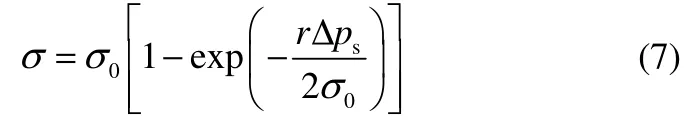
由于Kashchiev模型是以理想气体为条件推导的，而两相凝结流动十分复杂，与理想气体参数有很大不同，若以此修正存在一定困难。本文将采用Tolman模型对张力进行修正。

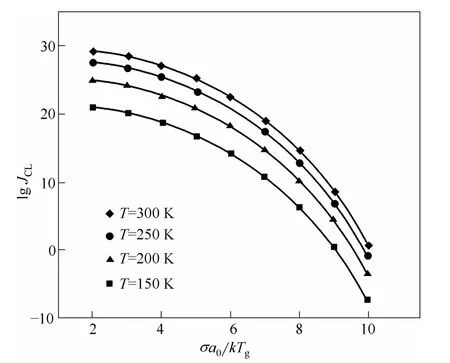
图1 成核率与表面张力的关系 Fig.1 Relationship between surface tension and nucleation rate

1.3 热质平衡耦合模型

按照气体动力学理论，水分子对凝结核的撞击频率与其平均自由程以及水滴半径有关。一般用量纲1参数Knudsen数（Kn）衡量水分子与凝结核的碰撞情况，Kn越大，凝结核相对于周围水分子的分布情况越小[11-13]。Kn是一个控制质量、能量流量的重要参数，根据其取值不同，可将水滴与周围的环境组合分为3个区域[14]。

Gyarmathy等[7]基于Fick扩散率和Fourier导热率计算了Kn << 1和Kn>>1两种极限情况下的水滴生长率。Young[15-16]基于Gyarmathy模型，根据外层与中间层的通量匹配，讨论了不同Kn下的水滴生长模型，并在10～30 kPa下进行修正，得出β为影响中间层水滴生长速率的修正因子。Peters等[17]对比了Gyarmathy模型和Young模型，并指出Gyarmathy模型较Young模型有更好的效果。Gyarmathy水滴生长率计算式为

Young水滴生长模型为

根据Maxwell模型，水滴表面的质量交换可表示为

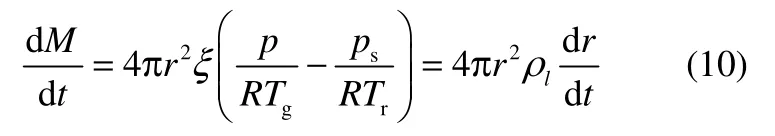
根据式(10)，得出水滴和蒸汽间的传热表达式

由于一次水滴的平均直径基本在1 μm以下，水滴内能变化远小于凝结换热量，因此式(11)右端第2项可以忽略。热质平衡耦合模型为

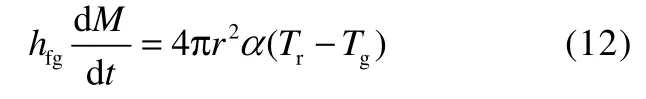
α可由量纲1传热系数Nusselt数(Nu)确定

由式（10）和式（12）联立，得出热质平衡耦合模型水滴生长率计算式为

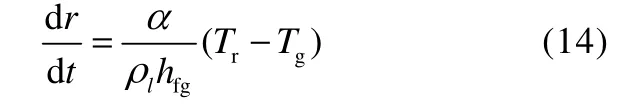
热质平衡耦合模型同时考虑了水滴生长中的传热和传质过程，可以求解整个Kn范围内的水滴凝结生长过程。本模型中的水滴温度由传质、传热方程耦合求解得出，具有较高的计算精度。

1.4 气体状态方程

凝结流动一般出现在饱和线以下较低温度和压力的区域，此处水蒸气热力学参数与理想气体有很大差异。本文计算时采用Young提出的维里型气体状态方程

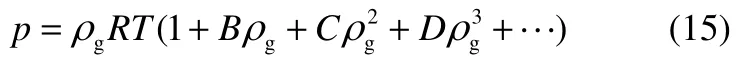
式中，B、C、D为二至四阶维里系数。对于工程计算，二阶维里方程即可满足计算精度要求。二阶维里系数B表达式

式中，τ=1500/T，a=10000.0，a1=0.0015，a2= -0.000942，a3= -0.0004882。

当前，研究湿蒸汽跨声速凝结流动的高分辨率差分格式主要有TVD、NND、失通量分裂格式等[18-19]。文献[20]给出了两相流动的控制矩阵，并推导了特征值和特征向量，运用TVD格式、时间推进法进行求解。本文采用二阶TVD格式对两相流控制方程进行离散，具有较好的激波捕获效果。

2 非平衡凝结流动的热力学特性

2.1 模型验证

为了验证本文数值模型的可靠性，采用Tolman模型对成核率进行修正，水滴生长率计算分别采用Gyarmathy模型、Young模型和本文模型，对Laval喷管中的蒸汽非平衡凝结流动进行仿真，喷管型线见图2。喷管入口直径为8 cm，出口直径为4.746 cm，喉部位于x=0处，喷管总长度23 cm。

图2 Laval喷管几何结构数据 Fig.2 Geometry data of Laval nozzle

流动条件：进口总压P0t=87 kPa，总温T0t= 390.15 K，出口为超声速流动，喷管压力分布实验数据取自文献[7]，图3给出了喷管轴线处压比分布。凝结冲波位置、波形与实验值吻合度较好，说明本文建立的数值模型是可靠的。与Gyarmathy模型和Young模型相比，本文模型仅在凝结冲波位置有所差异。Young模型的压力突跃更加明显，而本文模型的压力突跃介于Gyarmathy模型和Young模型之间，因此本文模型所获得的结果精度基本与其他模型相近。为了更好地揭示凝结冲波对两相流的影响，图3也给出了等熵模型的计算结果。

图4给出了此工况主要凝结流动参数的计算结果，由图可以看出气液两相参数随蒸汽膨胀的变化规律。过热蒸汽在Laval喷管中膨胀时，过冷度ΔT不断提高。在喷管上游x=-1.49 cm处过冷度为0，蒸汽处于饱和状态；在喷管下游x=1.72 cm处过冷度达到最大值36.25 K，蒸汽处于过饱和状态，凝结突然出现。成核率在短时间内由0上升到2.56×1022，水滴数目也急剧增加到1017数量级。由于凝结释放的大量潜热引起了凝结冲波，在较高的过冷度下水分子开始在临界水滴表面凝结，水滴开始生长。

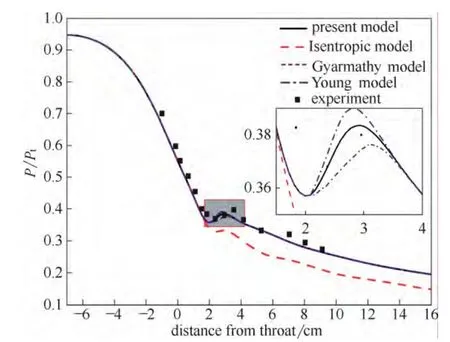
图3 喷管轴线压比与实验值的比较 Fig.3 Pressure ratio along nozzle axis compared with experimental value

图4 主要凝结参数沿喷管轴线分布 Fig.4 Main condensing parameter distribution along nozzle axis

2.2 凝结流动变压特性

为了得出影响非平衡凝结特性和凝结冲波强度的热力学参数，对Laval喷管进行变工况计算。本文共设计了7种工况，见表1。

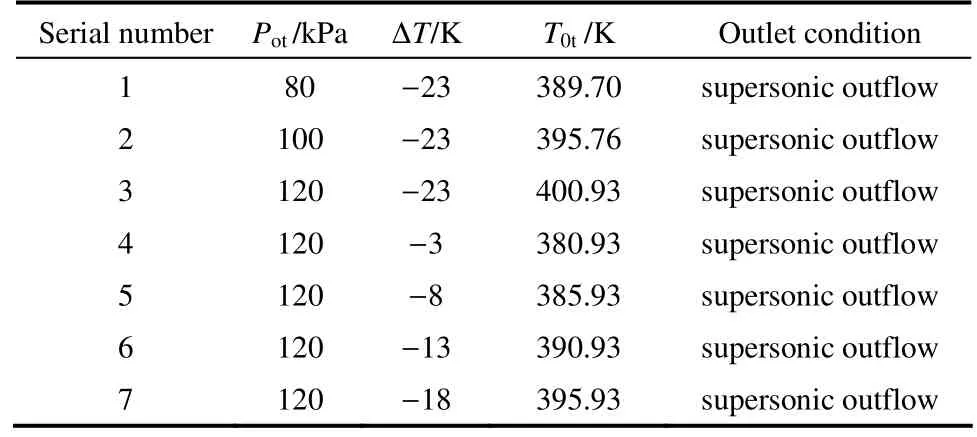
表1 喷管进出口参数表 Table 1 Boundary conditions for import and export of nozzle

工况1～工况3用于研究凝结冲波的变压特性；工况3～工况7用于研究过冷度对凝结冲波的影响。变压特性计算中取过冷度ΔT= -23 K，进口压力Pot分别为80、100、120 kPa，进口温度T0t分别为389.7、395.76、400.93 K。图5给出了不同进口压力下，喷管轴线处过冷度、成核率、水滴数、Mach数分布。

对比图5(a)、(b)可知，相同过冷度下，进口压力增加，凝结位置逐渐向上游移动，但移动幅度很小。3种工况的过冷度峰值相差不大，分别为36.97、35.98、35.14 K。随着进口压力的增加，凝结速度加快，成核率降低，由此导致水滴数目减少，但水滴半径增加。图5(d)给出了不同进口压力的Mach数分布，3种工况的Mach数曲线基本重合，只是在凝结冲波附近有较大差别，进口压力越大，凝结冲波的强度也越大。

2.3 进口过冷度特性

在2.2节的基础上，对Laval喷管进一步进行计算，讨论相同进口压力、不同过冷度下的湿蒸汽凝结特征。取进口压力Pot为120 kPa，进口过冷度ΔT分别为-3、-8、-13、-18、-23 K，研究过冷度升高对蒸汽非平衡凝结特性的影响。

图6给出了工况3～工况7喷管轴线处的压比、成核率、水滴数、湿度、过冷度、Mach数分布。由图6(a)可知，在凝结冲波出现之前，蒸汽压力不断降低，各工况压比曲线重合；当越过喉部后，蒸汽过冷度达到Wilson点并出现大量凝结核，大部分凝结潜热是在成核区释放的，同时伴随产生凝结冲波，压力在此处骤然升高。比较可知，入口过冷度越高，凝结冲波出现的位置越早。但是在较高过冷度下很难准确预测到凝结冲波出现的位置，此状态下的冲波结构是不稳定的。

对比图6(b)、(c)可知，进口过冷度越高，成核出现的位置越早，成核率也相应较小。过冷度开始下降后，成核现象迅速消失。

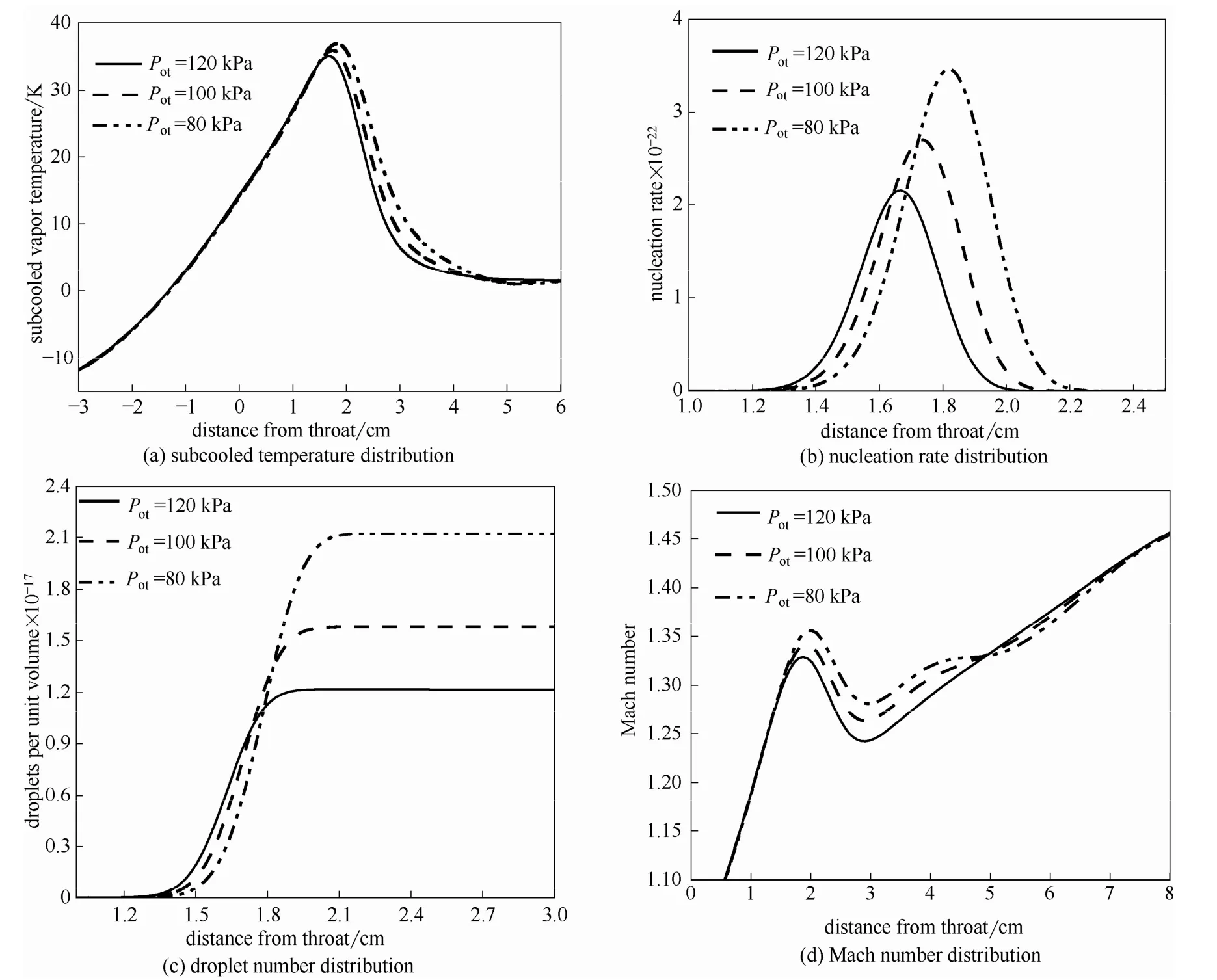
图5 不同进口压力的凝结流动参数 Fig.5 Condensing flow parameters of different inlet pressure

图6 不同进口过冷度的凝结流动参数 Fig.6 Condensing flow parameters of different inlet subcooled temperature

图6(d)给出了水滴数沿喷管中心轴线的分布情况。研究表明：进口过冷度是影响成核率的重要热力学参数，不同工况下的水滴数目差异较大。随着凝结成核的发生，各工况过冷度在喷管下游迅速降到了2 K左右，并不再出现新的凝结核，水滴数目基本保持不变。

图6(e)给出了各工况湿度分布，Laval喷管出口湿度随着进口过冷度的升高而逐渐升高。分析可知，在液相质量分数<0.005时，成核过程就基本完成了。由于凝结潜热使蒸汽处于低过冷状态，当水滴数量趋于稳定之后，水滴不断生长，因此湿度仍具有缓慢的上升趋势。

图6(f)给出了Mach数分布，在较高的进口过冷度下，蒸汽达到饱和状态后会迅速凝结成核。随着进口过冷度的降低，蒸汽需要在Laval喷管中加速一段距离，达到较高的过冷度后，才会出现成核现象。凝结冲波出现后，湿蒸汽沿Laval喷管继续高速流速，其流动规律与等熵流动相似。

3 结论

本文采用Tolman模型对经典成核率进行修正，引入热质平衡耦合模型对水滴生长速率进行计算，分析了非平衡凝结过程激波的分布规律。讨论了入口压力、过冷度对凝结特性的影响，总结了热力学参数对凝结位置、激波形态、流动参数的影响规律。并得出以下结论。

（1）相同进口过冷度下，随着进口压力增加，凝结位置逐渐向上游移动，成核率降低，水滴数目减少，但水滴半径增加。

（2）当总压为120 kPa时，随着过冷度由-3 K下降到-23 K，凝结位置逐渐向喷管下游移动，成核率也增加了1个数量级。

（3）进口压力相同时，Laval喷管出口湿度随着进口过冷度的升高而逐渐升高，当水滴数量趋于稳定之后，湿度仍具有缓慢的上升趋势。

符号说明

a0——单个气体分子的表面积，m2

cp——气体比热容，J·kg-1·K-1

e ——单位体积的能量密度，kJ·m-3

hfg——汽化潜热，kJ·kg-1

J ——单位体积成核率, (m3·s)-1

Kn ——Knudsen数

M ——水滴质量，kg

m ——单分子的质量，kg

N ——单位质量蒸汽水滴数

Nu ——Nusselt数

Prg——Prandtl数

P ——蒸汽实际压力，Pa

q ——凝结系数

R ——理想气体常数，J·(mol·K)-1

rc——水滴的半径，m

S ——过饱和度

Tr——水滴温度，K

ΔT ——过冷度，K

u ——轴向速度，m·s-1

v——径向速度，m·s-1

α ——水滴与蒸汽传热系数，W·(m2·K)-1

γ ——蒸汽比热容比

δ ——Tolman长度，m

ζ ——传质系数，m·s-1

θ ——量纲1表面张力

λg——蒸汽的热导率，W·(m·K)-1

μ ——水滴生长半经验修正系数

ρ ——密度，kg·m-3

σ0——液体表面张力，N·m-1

下角标

c——临界状态

g——气相

i——第i个水滴

l——液相

s——饱和状态

[1] Lin Zhirong(林智荣), Yuan Xin(袁新).A numerical method for spontaneous condensing flow and its application on Laval nozzle [J].Journal of Engineering Thermophysics(工程热物理学报), 2006, 27(1): 42-44.

[2] An Liansuo(安连锁), Wang Zhi(王智), Han Zhonghe(韩中合).Numerical simulation of wet steam two-phase flow in turbine cascade[J].Proceedings of the CSEE (中国电机工程学报), 2009, 29(11): 70-74.

[3] Han Zhonghe(韩中合), Chen Baiwang(陈柏旺), Liu Gang(刘刚), et al.Droplets growth model in wet steam two-phase condensation flow [J].Proceedings of the CSEE (中国电机工程学报), 2011, 31(29): 79-84.

[4] Bakhtar F, Tochai M T M.An investigation of two-dimensional flows of nucleating and wet steam by the time-marching method [J].International Journal of Heat and Fluid Flow, 1980, 2(1): 5-18.

[5] Bakhtar F, Young J B, White A J, et al.Classical nucleation theory and its application to condensing steam flow calculations [J].Proc.IMechE, 2005, (219): 1315-1333.

[6] Li L, Li Y, Wu L, et al.Numerical study on condensing flow in low pressure cylinder of a 300MW steam turbine//ASME Turbo Expo 2010: Power for Land, Sea, and Air[C].American Society of Mechanical Engineers, 2010: 2289-2296.

[7] Gyarmathy G, Lesch F.Fog droplet observations in Laval nozzles and in an experimental turbine//Proceedings of the Institution of Mechanical Engineers, Conference Proceedings[C].SAGE Publications, 1969, 184(7): 29-36.

[8] Patel Y, Patel G, Turunen-Saaresti T.The effect of turbulence and real gas models on the two phase spontaneously condensing flows in nozzle//ASME Turbo Expo 2013: Turbine Technical Conference and Exposition[C].American Society of Mechanical Engineers, 2013: V05BT25A018-V05BT25A018.

[9] Hill P G.Condensation of water vapor during supersonic expansion in nozzles [J].J.Fluid Mech., 1966, 25(3): 593-620.

[10] Bakhtar F, Zidi K.Nucleation phenomena in flowing high-pressure steam(Ⅱ): Theoretical analysis [J].Journal Proceedings of the Institution of Mechanical Engineers, 1990, 204(4): 233-242.

[11] Shen Shengqiang(沈胜强), Yang Yong(杨勇), Zhang Kun(张琨), et al.Condensation characteristics of supersonic non-equilibrium steam flow under different pressures [J].CIESC Journal(化工学报), 2010, 61(4): 820-824.

[12] Zhao Jiaquan(赵家权), Liu Peiqi(刘培启), Zhao Wenjing(赵文静), et al.Numerical analysis of unsteady condensation during expansion in shock tube [J].CIESC Journal(化工学报), 2012, 63(4): 1050-1055.

[13] Yang Yong(杨勇), Shen Shengqiang(沈胜强), Dong Guohai(董国海), et al.Effect of temperature on non-equilibrium phase change in transonic steam flow [J].CIESC Journal(化工学报), 2012, 63(2): 401-407.

[14] Su Jiqiang(宿吉强), Sun Zhongning(孙中宁), Gao Li(高力).Analysis of experiments for steam condensation in presence of non-condensable gases with moderate wall subcooling [J].CIESC Journal(化工学报), 2014, 65(10): 3884-3890.

[15] Young J B.The spontaneous condensation of steam in supersonic nozzles [J].Physicochemical Hydrodynamic, 1982, 3(1): 57-82.

[16] Young J B.Two-dimensional non-equilibrium wet-steam calculations for nozzles and turbine cascades [J].ASME J.Turbomach., 1992, 114: 569-579.

[17] Peters F, Meyer K A J.Measurement and interpretation of growth of monodispersed water droplets suspended in pure vapor [J].International Journal of Heat and Mass Transfer, 1995, 38(17): 3285-3293.

[18] Huang L, Young J B.An analytical solution for the Wilson point in homogeneously nucleating flows [J].Proceedings: Mathematical, Physical and Engineering Sciences, 1996, 452(1949): 1459-1473.

[19] Gerber A G, Sigg R, Völker L, et al.Predictions of non-equilibrium phase transition in a model low-pressure steam turbine [J].Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2007, 221(6): 825-835.

[20] Zhang Dongyang(张冬阳), Liu Jianjun(刘建军), Jiang Hongde(蒋洪德).The approach and application of fast and accurate numerical simulation on 3D wet steam flow [J].Journal of Engineering Thermophysics(工程热物理学报), 2003, 24(2): 262-264.