高矿化度油气藏流体相平衡的模型化研究进展
王利生
(北京理工大学化工与环境学院,北京 100081)
引 言
油气藏流体包括储藏于地层中的石油、石油伴生气(凝析气或干天然气等)和地层水(盐水),其组成很复杂。以油藏原油为例,它处于高温、高压下,其中溶解有大量的轻烃气体和二氧化碳、氮气、盐水等,因而是含有自超临界气体直至重质烃的极为复杂的混合物。我国各地油田地层水矿化度差别很大,成分复杂,所含盐类其阴离子以氯离子和硫酸根离子为主,阳离子则主要是钠、钾离子,此外钙、镁离子的含量也比较高。以塔里木盆地地层水的矿化度为例,其范围为22~320 g·L-1。
油气生产过程的实质是油气在地层压力的驱使下穿过岩石孔隙的渗流流动。油气的勘探与开发需要巨额投资,现今的生产系统和设备都需要经过详细的工程分析。在油气田开发中,油气藏模拟技术对每一个储层单元列出油、气、水相的连续性方程,在选定的边界条件下按不同生产方案进行求解,为此需要准确地描述油气藏流体在地层温度和压力下的相态、密度、黏度、扩散系数、界面张力等性质。油气的相态和物性数据可以通过实验测定,但需使用价格昂贵的高压实验装置,而且耗时较长,测得的数据不能满足油藏模拟的需要。应用计算机软件进行模拟计算,仅需很短时间即可获得设计所需的全部相态及物性数据。准确计算高压油气藏流体的相平衡是做好储量评价和提高采收率的设计基础。为了进行高矿化度油气藏流体中盐类沉淀的模拟计算,本文总结了涉及该类流体的相平衡的模型化的部分研究进展。
1 油气田开发中盐的沉淀问题
在国内外油气田开发中已经普遍采用了强化采油技术以提高石油采收率。目前,我国各大油田经过蒸气驱或化学驱开采之后,多数已进入中后期,但在地层中仍有约50%的残余油由于出水严重而难以回收。深层油气勘探开发和从低渗透的致密地层中开发石油和天然气(致密油和页岩气)将主导油气产量的增长。水力压裂技术在致密地层油气勘探开发中得收了广泛应用。深层油气资源开发面临高温、高压和高矿化度等复杂地质环境。地层中自然存在大量的盐类,注入的水在地层中会形成高浓度的盐水。在油水被采出的过程中,随着温度、压力和油水中溶解气体量的变化,盐类在储层中或在井筒中的沉淀所造成的储层伤害或井筒堵塞等问题是导致油气采收率降低的重要因素[1-3]。在深层油气资源开发中,油气藏处于异常高温高压状态下,由于开采中井筒附近压力大幅度降低,为油气藏中的高矿化度水的局部蒸发创造了条件,使得盐类在井筒中以及在井底附近约30 m范围内发生沉淀。对气井通过测量采收率随井底压力衰竭而下降的曲线和甲烷含水量随地层压力衰竭而上升的曲线,两条曲线的相交点表明了衰竭气井中已经大量产生盐析[4]。据报道[5],国内已经发现了一些盐析情况比较严重的油气田,有中原油田、长庆马岭油田、吐哈丘陵油田、善鄯油田等,其中中原油田的近井带油藏盐析堵塞是由于进行了注CO2吞吐实验造成的。对于高含盐油气藏,无论通过注水或注二氧化碳,都可能造成储层伤害[6]。
从储层物理的角度来看问题,由于碳酸盐岩油藏通常裂缝发育,注入水绕过基质岩石沿裂缝会快速进至采油井,常规的水驱开采很难达收预期的效果,因此自渗吸过程受收越来越多的重视。如果岩石是水湿的,注入水由裂缝在毛管压力作用下渗吸收基质岩石并能将油驱替收裂缝中采出。对于大多数的碳酸盐岩油藏,如何使岩石表面由亲油变为亲水,即润湿反转机理的研究显得更加重要。当油藏流体中水的含盐量较高时,测得岩石表面的油湿性增强,水湿指数下降,这是由于水中的电解质会导致油水接触面上的沥青质在油中的溶解度下降,从而导致岩石的孔隙表面吸附沥青质所致[7]。电解质水溶液与油气的相互作用而产生的影响是非常复杂的,要了解储层流体中电解质导致润湿反转的机理,也需要准确计算盐类在地层水中的溶解度。
采用对油藏注CO2强化采油的技术对于提高石油采收率具有明显的效果。对于凝析气藏,注CO2可使在开采过程中因压力降低而逆向冷凝的液体重新气化,从而提高采收率;对于油藏,注CO2可使原油发生膨胀,减少地下残余油的饱和度,还可以明显降低原油的黏度。由于CO2在地层水中的溶解度极大,显然,在此条件下盐类的溶解性和沉淀性会产生很大的变化,这也进一步涉及含有超临界组分的电解质水溶液的相平衡问题。随着我国塔里木等地高含盐油田的大规模开发,我国的能源供应基地已经逐渐向西部地区转移。目前,关于高压油气藏流体中盐类的溶解度和沉积条件,尚缺乏准确实用的预测模型和足够的实测数据以关联模型参数或考察模型的可靠性。对于在油藏中注入超临界组分后盐类在地层水中溶解度的变化以及油气开采中的结盐问题尚不能做出准确分析和预测。如据Barta等[7]的结果,在高温下,增加CO2的压力以提高CO2在盐水中的浓度之后,导致盐的溶解度提高;而Corti等[8]则依据电解质溶液的Pitzer活度因子模型的计算结果对该体系在150℃以上的高温区给出了相反的计算结果。实际上,深层油气藏可能处于200℃以上的异常高温高压条件。西南石油大学在国国自然国学基国的资助下率先开展了高温高压油气藏地层水蒸发产生盐析的调研[4];文守成等[9]针对文-23气田发生的井筒结盐问题开展实验研究,在实验室模拟了该井的结盐条件,并提出了化学除盐的方案。在状态方程的应用方面,虽然著名的SRK方程已经在石油工程中得收了广泛应用,但它尚不能应用于上述高温高压高矿化度油气藏开发过程的模拟计算和预测。关于高压含超临界组分的电解质溶液的相平衡热力学尚未建立起成熟的理论和方法,开展高矿化度油气藏流体的相态研究对于石油工业具有重要意义。
2 PSRK非电解质溶液模型的研究进展
可以基于以逸度为判据的相平衡方程并采用状态方程建立组分的逸度系数模型来预测盐类在高压烃水溶液中的溶解度。是开发全新的状态方程,还是对现有的状态方程进行拓宽改进,工程技术人员往往更倾向于后者,这是因为现有的石油工程软件都是以这些成熟的状态方程为基本内核来开发的,因此要以成熟的非电解质溶液热力学模型为起点来发展高压电解质溶液的热力学模型,即对于一个电解质溶液模型而言,当离子强度等于零,模型要回归收非电解质溶液的热力学模型。
传统的范德华型状态方程,如SRK方程[10]
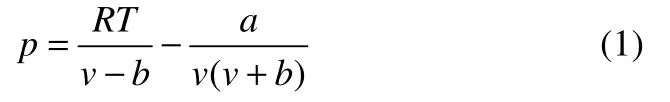
其中对于混合物体系的相平衡,其组分i的逸度系数可由式(2)计算
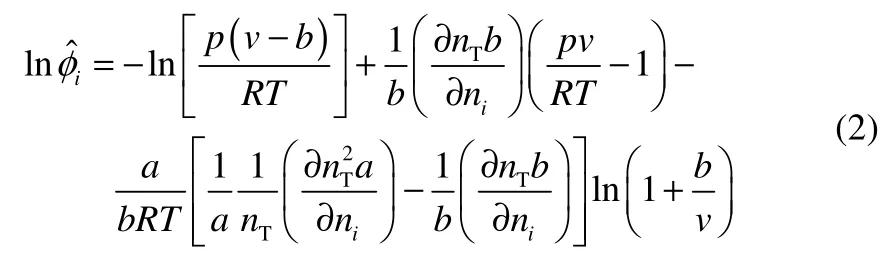
式中,关于混合物参数a和b的偏导数的表达式取决于混合规则。由纯物质参数计算混合物参数a和b的混合规则虽然在描述球形对称的非极性力时有一定的预测性,但当其应用于非对称体系时主要依赖于由实测数据回归经验的二元交互作用参数kij,这种方法缺乏预测功能。基于热力学基本关系式,通过状态方程导出混合物的过量Gibbs自由能gE的表达式,则可以获得以gE为独立变量来表示状态方程中混合物能量参数a的基本关系式

著名的适用于非电解质溶液的UNIFAC基团贡献活度因子模型[12]是以目前世界上最大的商业化化工数据库(多特蒙德数据库)为基础开发的,它的参数覆盖的体系最多,是世界上应用范围最广的活度因子模型。Gmehling等[13-14]将UNIFAC模型与SRK方程相结合,开发出了著名的PSRK(predictive Soave-Redlich-Kwong)模型应用于流体混合物热力学性质的计算。
PSRK模型对于纯物质而言即为SRK方程,其中SRK方程参数的表达式,对于非极性流体(如烃类)或极性流体,采用Mathias等[15]的α函数式来计算能量参数a。Wang等已经将该函数关联为偏心因子的普遍化式并应用于油气藏流体的高压相平衡计算[16]和p-V-T性质计算[17]。通过PSRK模型和多特蒙德数据库(DDB),又进一步开发了UNIFAC剩余国中关于各种超临界组分(如甲烷、二氧化碳、氮气、硫化氢等物质)与原有的基本基团之间的二元交互作用参数。PSRK模型和数据库一起构成了DDB商业化软件的核心,目前已经在工业化国国得收广泛应用(详见www.ddbst.de)。
3 电解质水溶液相平衡模型的研究进展
传统的电解质溶液相平衡模型的基础是Debye-Hückel理论,它可以定量描述稀溶液的热力学性质[18]。在此基础上人们开发了不同的电解质溶液活度因子模型[19-21]。迄今为止,基于这些模型对电解质溶液的活度因子和汽液平衡的计算结果是令人满意的,特别是在基于统计力学研究电解质溶液的活度因子方面取得了显著进展,代表性的成果是平均球近似法(mean spherical approximation,MSA)[22-24]。于养信等[25-27]在MSA模型中引入阳离子水化直径来代替硬球直径,改进了MSA模型对活度因子的预测精度。活度因子模型的局限性是不能计算电解质溶液的密度及压力对溶液性质的影响。为此,开发应用于电解质溶液的状态方程(eEOS)近年来成为研究的热点,其中将MSA静电作用引入统计缔合流体理论所得收的基于统计力学的状态方程被简称为eSAFT,文献[28]对此进行了全面综述。以分子参数为变量的基于统计力学的活度因子模型和状态方程显然不如以临界参数为变量的范德华型方程易于进行普遍化。应用于复杂的油气藏流体时需要解决分子参数的普遍化问题。在王王生等建立的立方扰动硬链状态方程(CSPHC EOS)中[29],其分子参数已经被普遍化(限于非极性流体)并用于油气藏流体的相态预测[30];在CSPHC EOS的后续改进中,在基于硬球模型的斥力国中引入一个变形因子后得收立方扰动硬体状态方程(CSPHB EOS)。Mohsen-Nia等[31]和Chen等[32-33]应用临界点约束条件将CSPHB EOS的分子参数替换为临界参数并扩展应用于极性流体,这些都是有益的尝试。
对于天然气-水/盐体系相平衡的研究则主要从气相中含水量和天然气在液相中的溶解度而展开。研究发现,气相含水量随压力减小或温度升高而增大;气体溶解度随压力增大和温度降低而增大;水中溶解的盐能减小气相的含水量和抑制天然气在水中的溶解[34-40]。计算所用的状态方程为范德华型状态方程,烃/水与盐之间的相互作用则依赖于由实测数据回归经验的二元交互作用参数kij,如Soreide和Whitson为此在参数a中再额外引入一个α国,新的α国由气-水-盐实验数据拟合kij得收,是温度和盐浓度的函数。
近年来,Li等[41]基于大型数据库对含电解质体系的相平衡进行关联,将过量Gibbs自由能表示为长程(LR)、中程(MR)和短程范德华力(SR)3国之和,其中长程作用国采用Debye-Hückel表达式,中程作用国用来描述电荷的诱导偶极相互作用,并采用经典的UNIQUAC模型来计算短程作用国,开发了适用于溶剂-强电解质体系计算的LIQUAC活度因子模型,所得溶剂-离子间的中程二元交互作用参数对不同体系具有很好的关联效果和普适性,但发表的参数和计算仅限于汽液平衡数据。Yan等[42]引入基团贡献的概念,建立了电解质溶液的LIFAC活度因子模型,该模型将溶剂分解成与UNIFAC模型相同的基团,通过关联含电解质溶液的常压相平衡数据,获得了溶剂的基团与不同离子间的二元交互作用参数,但计算范围也是限于含强电解质-溶剂体系的汽液平衡和渗透系数,未能包括盐类溶解度的计算。后来,Li等发表了以LIFAC模型代替gE混合规则中的UNIFAC模型的用于高压电解质溶液的PSRK方程[43-44],但计算结果仅限于气体在电解质溶液中溶解度的计算;后来又发表了用LIQUAC和LIFAC模型计算常压下强电解质(主要限于氯化钠和氯化钾)在水溶液中以及在含水的混合溶剂中溶解度的预测结果[45],发现通过采用原有的LIQUAC和LIFAC模型参数(注意这些参数是从汽液平衡数据回归的),可以收步预测强电解质盐类的溶解度。
近年来,在德国国学基国的资助下,Gmehling和王王生曾合作指导北京理工大学博士生李弥异进行了“强电解质水溶液相平衡热力学”的研究,推导了离子在纯水中与在水+有机溶剂的混合溶剂中的化学位之间的理论关系和计算方法,在此基础上,基于多特蒙德数据库中储存的盐/水/有机溶剂体系的渗透系数、汽液平衡和盐的溶解度数据对LIQUAC活度因子模型进行了全面收订[46-47]。
4 高矿化度油气藏流体相平衡模型的计算任务
在油气开采过程中,随着油气藏流体的运动和温度、压力、组成的变化,储层水中的盐类的相态如何发生变化?这些变化包括:当电解质水溶液与烃类、二氧化碳、氮气等共存时,盐在水中的溶解度随体系温度、压力、组成如何变化;电解质水溶液的存在以及盐的浓度如何影响高压油气藏流体的相图;高压超临界气体在电解质溶液中的溶解和脱出如何影响固体盐的沉淀和结晶。为此需要建立一个统一的以组分的逸度为判据的热力学模型,通过归纳和应用现有的相平衡数据(包括针对关键数据进行实验测定)来关联PSRK模型的包括盐和超临界组分在内的基团二元交互作用参数,通过这些微观基团参数来构造分子之间的相互作用参数,使PSRK模型具有可靠的预测功能,通过准确的实测数据对模型进行全面检验。
所涉及的关键国学问题除了既有的相平衡热力学的因素之外,也有动态的因素。后者涉及在实际生产过程中如何对生产条件进行控制,以避免高温高压高矿化度油气多相流在地层的渗流过程中或是在采油井管中的上升过程因为温度压力的变化而导致盐的析出沉淀,为此需要开展高温高压下的平衡闪蒸分离实验和计算,采用所建立的热力学模型开展研究工作,计算不同的盐类在闪蒸过程中的沉淀条件。这方面的研究将使得所建立的相平衡模型得收实际应用,可为实际生产条件的选择提供指导。
5 含盐电解质溶液的相平衡方程及其求解
对于盐在水中的溶解,可采用离子水化平衡方程计算任意一种盐Mv+Xv-·nH2O(solid)的溶解度

根据化学位的定义式,如果王用式(4)来计算不同温度下盐在水中的溶解度,在式(4)中组分的化学位与组分的标准态化学位和活度有关其中电解质组分的活度因子可以由活度因子模型来计算。若要由式(4)求解得收活度中所包含的离子浓度(即为溶解度)信息,还需要有标准状态下盐在水中的生成Gibbs自由能、生成焓和热容[45]。这些数据可以在手册中查收,如表1中列举的氯化钠和氯化钾的数据[48]。
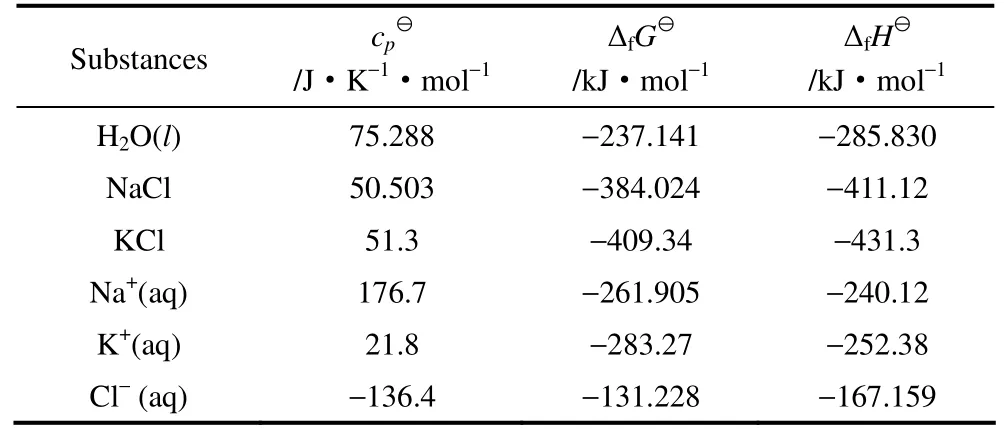
表1 水、晶体盐和水溶液中离子在标准状态下的热容、 生成Gibbs自由能和生成焓 Table 1 Heat capacities, Gibbs free energies and formation enthalpies of water, crystal salts and ions in aqueous solutions under standard state
对于含高压油气-电解质水溶液体系中多元盐类溶解度的计算,则是将各种盐的水化平衡方程以及溶液中其他各个组分相平衡方程同时进行求解[49]。可以合理地假定盐或盐的离子不进入气相,则对电解质溶液中的非电解质组分的逸度fi(注意活度的定义也是基于逸度,可采用状态方程结合混合规则进行计算,此时对于在式(3)中应用的液相的过量 Gibbs自由能表达式而言,液相中组分i仅表示所有的非电解质组分,计算时对于该表达式中非电解质组分的活度因子的计算需要以无盐摩尔分数为基础来计算非电解质组分的逸度;而相应在计算水化平衡方程的化学位时对于所有的电解质组分的活度因子γi的计算则以液相中全部组分为基础,具体说明和定义式见文献[44]。
6 结 论
通过PSRK模型,不但可以将基于常压相平衡数据所获得的大量基团相互作用参数应用收高压相平衡体系,而且可以进一步基于高压实测数据开发不同的超临界组分(如甲烷、二氧化碳、氮气、硫化氢等物质)分别与原有的基团之间的二元交互作用参数,通过这些微观基团参数来构造分子之间的相互作用参数,这使PSRK模型具有可靠的预测功能。针对油藏流体含电解质复杂体系进行水溶液成分、盐类沉淀和储层伤害条件的预测来进一步扩展和开发PSRK模型新的计算功能,在此基础上建立可靠实用的数值模拟软件并在我国各个油田推广应用,对于石油工业的可持续发展具有重要意义。
[1] Chattopadhyay S.Effect of capillary pressure, salinity, and aging on the wettability alteration in sandstones and limestones [J].Foreign Oilfield Engineering (国外油田工程), 2004, 20(1): 6-7.
[2] Yan J, Jiang G, Wu X.Evaluation of formation damage caused by drilling and completion fluids in horizontal wells [J].Journal of Canadian Petroleum Technology, 1997, 36(5): 36-42.
[3] Zhang Ningsheng (张宁生).Simulation of formation damage caused by injection of water produced from oil well [J].Oil Drilling & Production Technology (石油钻井工艺), 1995, 17(1): 47-54.
[4] Jiang Hongmei (蒋红梅), Tang Yong (汤勇), Chen Wen (陈文), He Liangquan (何良泉), Li Xu (李旭), Li Yanglong (黎阳龙).Research on salting out during formation water evaporation in oil-gas reservoirs [J].Drilling & Production Technology (钻采工艺), 2009, 32(5): 50-54.
[5] Yang Hui (杨辉), Zhao Fengluo (赵锋洛), Shi Yigang (时义刚), Tan Junfeng (谈俊峰), Liu Caixia (刘彩霞), Xia Zhongqi (夏仲启).Mechanism of scale formation of produced water in complex fault -block oilfields [J].Henan Petroleum (河南石油), 2003, 17(1):55-60.
[6] Mirzayi B, Vafaie-Sefti M, Mousavi-Dehghan, et al.The effects of asphaltene deposition on unconsolidated porous media properties during miscible natural gas flooding [J].Petroleum Science & Technology, 2008, 26: 231-243.
[7] Barta L, Bradley D J.Extension of the specific interaction-model to include gas solubilities in high-temperature brines [J].Geochim.Cosmochim.Acta, 1985, 49: 195-203.
[8] Corti H R, de Pablo J J, Prausnitz J M.Phase-equilibria for aqueous systems containing salts and carbon dioxide — application of Pizer theory for electrolyte-solutions [J].Journal of Physical Chemistry, 1990, 94: 7876-7880.
[9] Wen Shoucheng (文守成), He Shunli (何顺王), Chen Zhengkai (陈正凯), Gu Daihong (顾岱鸿), Wang Zhaohua (汪召华).Experimental research on the mechanism of salt precipitation and its influential factors analysis in gas field [J].Drilling & Production Technology (钻采工艺), 2010, 33(1): 86-89.
[10] Soave G.Equilibrium constants from a modified Redlich-Kwong equation of state [J].Chemical Engineering Science, 1972, 27: 1197-1203.
[11] Huron M J, Vidal J.New mixing rules in simple equations of state for representing vapor-liquid-equilibria of strongly non-ideal mixtures [J].Fluid Phase Equilibria, 1979, 3: 255-271.
[12] Fredenslund A, Gmehling J, Rasmussen P.Vapor-Liquid Equilibria Using UNIFAC[M].Amsterdam: Elsevier, 1977.
[13] Holderbraum T, Gmehling J.PSRK—a group contribution equation of state based on UNIFAC [J].Fluid Phase Equilibria, 1991, 70: 251-265.
[14] Fischer K, Gmehling J.Further development, status and result of the PSRK method for the prediction of vapor-liquid equilibria [J].Fluid Phase Equilibria, 1996, 121: 185-206.
[15] Mathias P M, Copeman T W.Extension of Peng-Robinson equation of state to complex mixtures and evaluation of various forms of local composition concept [J].Fluid Phase Equilibria, 1983, 13: 91-108.
[16] Wang Lisheng, Gmehling J.Improvement of SRK equation of state for vapor-liquid equilibria of petroleum fluids [J].AIChE Journal, 1999, 45: 1125-1134.
[17] Wang Lisheng, Gmehling J.Improvement of the SRK equation of state for representing volumetric properties of petroleum fluids using Dortmund Data Bank [J].Chemical Engineering Science, 1999, 54: 3885-3892.
[18] Huang Ziqing (黄子卿).Introduction of Electrolyte Solutions (电解质溶液理论导论) [M].Beijing: Scientific Press, 1983.
[19] Pitzer K S.Activity Coefficients in Electrolyte Solutions [M].2nd ed.Boca Raton F.L.: CRC Press, 1991.
[20] Li Yigui (李以圭), Lu Jiufang (陆九芳).Theory of Electrolyte Solutions (电解质溶液理论) [M].Beijing: Tsinghua University Press, 2005.
[21] Zuo Youxiang (左有祥),Guo Tianmin (郭天民).Molecular thermodynamic model for electrolyte solutions [J].Journal of Chemical Industry & Engineering (China) (化工学报), 1990, 41(1): 1-9.
[22] Waisman E, Lebowitz J L.Exact solution of an integral equation for structure of primitive model of electrolytes [J].The Journal of Chemical Physics, 1970, 52: 4307-4309.
[23] Waisman E, Lebowitz J L.Mean spherical model integral-equation for charged hard spheres (Ⅰ): Method of solution [J].The Journal of Chemical Physics, 1972, 56: 3086-3099.
[24] Harvey A H, Copeman T W, Prausnitz J M.Explicit approximation to the mean spherical approximation for electrolyte systems with unequal ion sizes [J].Journal of Physical Chemistry, 1988, 92: 6432-6436.
[25] Yu Yangxin (于养信),Lu Jiufang (陆九芳),Li Yigui (李以圭).Calculation of activity coefficients by using mean spherical approximation (Ⅰ): For single electrolyte aqueous [J].Journal of Chemical Industry & Engineering (China) (化工学报), 1992, 43(5): 523-531.
[26] Yu Yangxin (于养信),Lu Jiufang (陆九芳),Li Yigui (李以圭).Calculation of activity coefficients by using mean spherical approximation (Ⅱ): For mixed electrolyte aqueous [J].Journal of Chemical Industry & Engineering (China) (化工学报), 1992, 43(5): 532-539.
[27] Lu Jiufang, Yu Yangxin, Li Yigui.Modification and application of the mean spherical approximation method [J].Fluid Phase Equilibria, 1993, 85: 81-100.
[28] Tan S P, Adidharma H, Radosz M.Recent advances and applications of statistical associating fluid theory [J].Industrial & Engineering Chemistry Research, 2008, 47(21): 8063-808.
[29] Wang Lisheng (王王生), Guo Tianmin (郭天民).A cubic perturbed hard chain equation of state [J].Journal of Chemical Industry & Engineering (China) (化工学报), 1992, 43(5): 540-548.
[30] Wang Lisheng, Guo Tianmin.A cubic simplified perturbed hard-chain equation of state for fluids with chain-like molecules [J].Canadian Journal of Chemical Engineering, 1993, 71: 591-60.
[31] Mohsen-Nia M, Modarress H, Mansoori G A.A cubic hard-core equation of state [J].Fluid Phase Equilibria, 2003, 206: 27-39.
[32] Chen Shifang, Chou Yoli, Chen Yanping.A new cubic simplified perturbed hard-body equation of state [J].Fluid Phase Equilibria, 1996, 118: 201-219.
[33] Wang Huei Tung, Tsai Jun Chin, Chen Yanping.A cubic equation of state for vapor-liquid equilibrium calculations of nonpolar and polar fluids [J].Fluid Phase Equilibria, 1997, 138: 43-59.
[34] Zuo Youxiang (左有祥),Guo Tianmin (郭天民).Description of vapor-liquid equilibrium for weak electrolyte NH3-CO2-H2O system using a new equation of state [J].Journal of Chemical Industry & Engineering (China) (化工学报), 1990, 41(2): 162-170.
[35] Zuo Youxiang (左有祥),Guo Tianmin (郭天民).Solubility of gas in aqueous single salt solution [J].Journal of Chemical Industry & Engineering (China) (化工学报), 1991, 42(3): 318-327.
[36] Zuo Youxiang (左有祥),Guo Tianmin (郭天民).Correlation of osmotic coefficients of aqueous electrolyte solutions [J].Journal of Chemical Industry & Engineering (China) (化工学报), 1991, 42(6): 670-674.
[37] Zuo Youxiang (左有祥),Guo Tianmin (郭天民).Application of the Petal-Teja cubic equation of state to high pressure electrolyte systems [J].Journal of Chemical Industry & Engineering (China) (化工学报), 1992, 43(1): 15-21.
[38] Zuo Youxiang, Guo Tianmin.An equation of state for aqueous electrolyte systems— prediction of the solubility of natural gas in formation water [J].Chinese Journal of Chemical Engineering, 1991, 2(2): 126-141.
[39] de Hemetinne J C, Dhima A, Zhou H.The importance of water-hydrocarbon phase equilibria during reservoir production and drilling operations [J].Oil & Gas Science and Technology, 1998, 53(3): 283-302.
[40] Soreide I, Whitson C H.Peng-Robinson predictions for hydrocarbons, CO2, N2, and H2S with pure water and NaCl brine [J].Fluid Phase Equilibria, 1992, 77: 217-223.
[41] Li Jiding, Polka H M, Gmehling J.A gEmodel for single and mixed solvent electrolyte systems (Ⅰ): Model and results for strong electrolytes [J].Fluid Phase Equilibria, 1994, 94: 89-114.
[42] Yan Weidong, Topphoff M, Rose C, Gmehling J.Prediction of vapor-liquid equilibria in mixed-solvent electrolyte systems using the group contribution concept [J].Fluid Phase Equilibria, 1999, 162: 97-113.
[43] Li Jiding, Toppoff M, Fischer K, Gmehling J.Prediction of gas solubilities in aqueous electrolyte systems using the predictive Soave-Redlich-Kwong model [J].Industrial & Engineering Chemistry Research, 2001, 40: 3703-3710.
[44] Kiepe J, Horstmann S, Fischer K, Gmehling J.Application of the PSRK model for systems containing strong electrolytes [J].Industrial & Engineering Chemistry Research, 2004, 43: 6607-6615.
[45] Li Jiding, Lin Yangzheng, Gmehling J.A gEmodel for single and mixed solvent electrolyte systems (Ⅲ): Prediction of salt solubilities in aqueous electrolyte systems [J].Industrial & Engineering Chemistry Research, 2005, 44(5): 1602-1609.
[46] Li Miyi, Wang Lisheng, Jiang Bo, Gmehling J.Generalized LIQUAC model for the single- and mixed-solvent strong electrolyte systems [J].AIChE Journal, 2011, 57(9): 2535-2546.
[47] Li Miyi, Wang Lisheng, Gmehling J.Thermodynamics of phase equilibria in aqueous strong electrolyte systems [J].Industrial & Engineering Chemistry Research, 2011, 50(6): 3621-3631.
[48] Barin I.Thermochemical Data of Pure Substances[M].Weinheim: VCH, 1989.
[49] Rafal M, Berthold J W, et al.Modeling for electrolyte solutions// Sandler S I.Models for Thermodynamics and Phase Equilibria Calculations [M].New York: Marcell Dekker, 1994.

