基液氨浓度对卡琳娜循环不同目标参数的影响

李惟毅，梁娜，孟金英，贾向东，李志会

（1天津大学中低温热能高效利用教育部重点实验室，天津 300072；2北京源深节能技术有限责任公司，北京100142；3天津市宝坻区益安机动车检测有限公司，天津 301800）

随着能源危机日益严峻，中低温余热能源逐渐进入人们的视野。卡琳娜循环（KCS34）作为一种适用于中低温余热的发电技术也被广泛关注，它是一种以氨水作为工质的动力循环系统，氨水作为一种非共沸混合工质，其相变过程存在温度滑移，所以蒸发过程温度变化曲线接近于热源温度变化曲线，有利于减小换热过程不可逆损失，提高热源利用率[1]。

为了更好地将卡琳娜循环应用于生产，国内外很多学者对其进行了研究，文献[2-3]对卡琳娜循环发电系统中氨水混合物的热力学参数进行了分析。在热力学循环性能方面，天津大学Fu等[4]对基于油田发电系统中卡琳娜循环子系统进行了讨论，分析了基液氨浓度（此处浓度是NH3·H2O在水溶液中的质量分数，下同）在0.55～0.95变化时，系统循环热效率、 效率、泵功随汽轮机进口压力的变化规律，得出实际中氨水浓度和汽轮机进口压力应比最佳点略低。重庆大学何嘉城等[5]对基液氨浓度在0.55～0.9时的卡琳娜循环系统进行了热力学分析，分析了汽轮机进口参数对循环性能的影响，并对各部件损进行了分析。文献[6]采用遗传算法对太阳能驱动的卡琳娜循环进行了热力学分析及优化，结果表明，在给定条件下，存在一个最佳汽轮机进口压力使效率达到最佳值。文献[7-8]从热力学与经济学角度对用于低温地热水系统的卡琳娜系统和ORC系统进行了比较。Arslan[9]对冰岛胡萨维克的卡琳娜循环系统进行了试验运行，分析了基液氨浓度取82%、富氨蒸汽浓度取95%时不同热源温度下系统的发电情况。天津大学任慧琴等[10]分析了基液氨浓度在0.22～0.66时不同蒸发器入口温度下基液氨浓度对卡琳娜循环理论热效率的影响。上述文献都主要集中于对卡琳娜循环热力性能的研究，而对其经济性研究较少。对于卡琳娜循环而言，换热器的换热面积、汽轮机尺寸在很大程度上影响系统经济性，而基液氨浓度作为卡琳娜循环的一个重要参数，其对系统的热性能、经济性都有很大的影响。故本文旨在分析热源吸热量一定的条件下基液氨浓度a对系统热效率、换热器换热性能及汽轮机尺寸参数的影响，并在此基础上分析其对系统经济性和系统综合性能的影响，最终得出综合性能最优时系统所对应的最佳基液氨浓度。

1 卡琳娜循环系统及目标函数的 建立

1.1 卡琳娜循环系统

卡琳娜循环系统由蒸发器、冷凝器、高温回热器、低温回热器、工质泵、分离器、汽轮机、节流阀、吸收器组成。其系统原理如图1所示，低温基液氨溶液通过冷凝器出口（状态点5）依次经过工质泵、低温回热器、高温回热器、蒸发器升温升压后进入气液分离器（状态点9），在分离器中，气液两相的基液被分为饱和富氨蒸汽（状态点1）和饱和富水溶液（状态点10），其中富氨蒸汽进入汽轮机做功，富水溶液通过高温回热器后节流降压与汽轮机出口乏汽在混合器进行混合，混合后的基液溶液依次通过低温回热器、冷凝器降温，然后进入工质泵，如此完成一个循环。

1.2 计算过程中所作假设及初始参数的确定

（1）设备连接管道的阻力忽略不计。

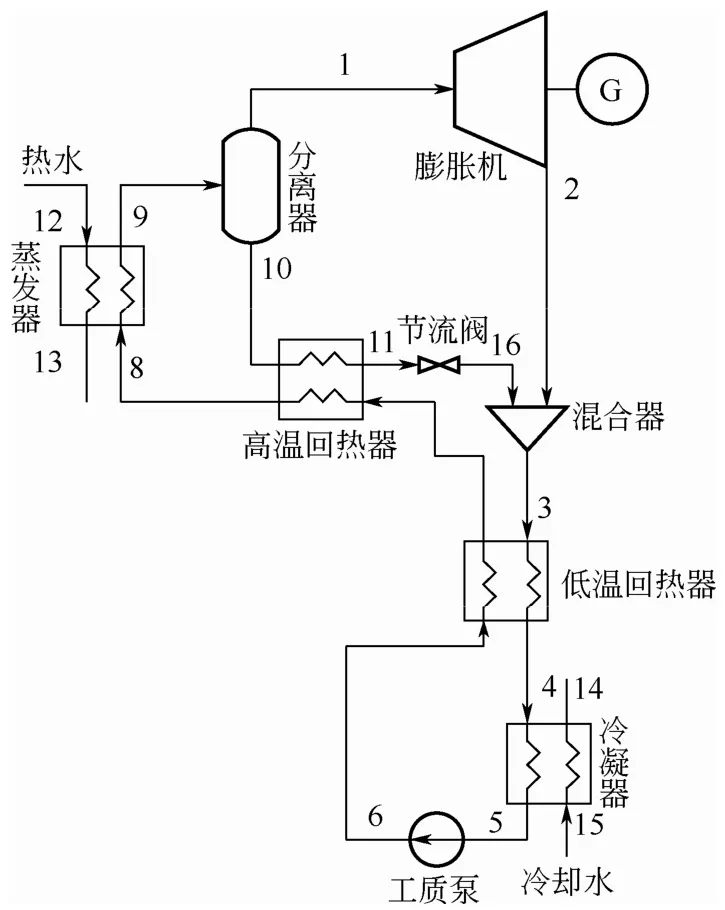
图1 卡琳娜循环系统（KCS34）原理图 1～16—状态点

（2）换热器压降100kPa。

（3）汽轮机机械损失、混合器压力损失忽略 不计。

（4）系统在稳定条件下运行。

（5）汽轮机内效率ηT为75%。

（6）各换热器换热效率η为95%。

（7）蒸发器、冷凝器最小换热温差为5℃。

（8）蒸发器热源热水入口温度为120℃。

（9）热水质量流量qm,w为50kg/s。

（10）蒸发器热源温降为40℃。

（11）冷凝器冷却水入口温度20℃。

（12）水的比热容c为4200 J/(kg·K)。

1.3 计算过程中所涉及到的公式

计算过程中所涉及的公式见式（1）～式（16），公式中所涉及的下角标与图1中各状态点一一对应。

基液质量流量

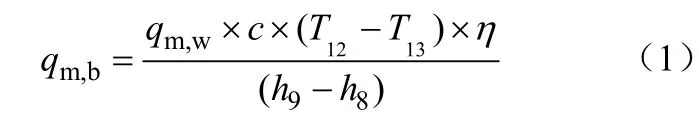
富水溶液质量流量

富氨蒸汽质量流量

汽轮机实际出口富氨蒸汽比焓

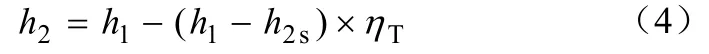
式中，h2s为汽轮机等熵膨胀出口富氨蒸汽比焓；h2为汽轮机出口富氨蒸汽实际比焓。

膨胀功

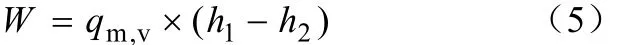
泵功

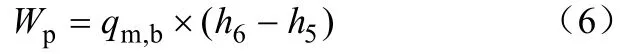
系统净输出功

冷却水质量流量

蒸发器换热量

高温回热器换热量

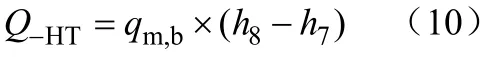
低温回热器换热量

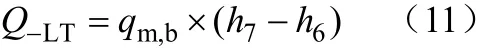
冷凝器换热量

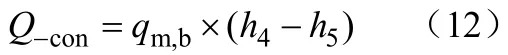
蒸发器对数平均温差

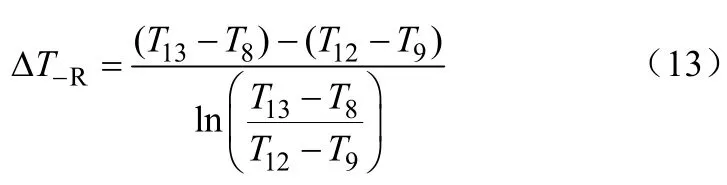
高温回热器对数平均温差

低温回热器对数平均温差

冷凝器对数平均温差

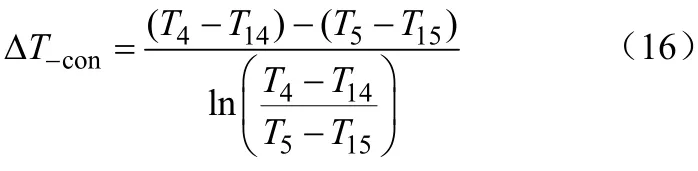
1.4 目标函数的建立

1.4.1 单目标函数的建立

（1）系统热效率 热效率反映了系统热功转化能力，热效率越高系统热力学性能越好。

（2）换热器经济参数 对于卡琳娜循环系统，换热器换热面积越大，系统投资费用越高，为了提高系统的经济性，应该尽可能减小换热器的换热面积，而在传热系数变化不大的情况下，换热器的换热量与换热器的对数平均温差的比值Q/ΔTm可以反映换热器的换热面积。同时为了反映单位净输出功所对应的换热器经济性，采用式（18）描述换热器的经济性[11]。AP的值越小，换热器经济性越好。

（3）汽轮机尺寸参数 在卡琳娜系统中，汽轮机尺寸越小，其费用投资就越小，经济性越好。根据相似性原理得出汽轮机尺寸参数可以通过汽轮机出口流体的体积流量和汽轮机进出口焓降表示，其尺寸参数的表达式可用式（19）表示[12]。在系统设计过程中，汽轮机尺寸参数TP越小，对经济性越有利。

式中，qv2为汽轮机出口工质体积流量；h1和h2分别为汽轮机进出口比焓。

1.4.2 多目标函数的建立

上述目标函数都只是从单一角度对系统进行分析，为了更全面地分析基液氨浓度对系统性能的影响，需要采用多目标综合分析法对其进行分析，而线性加权和法则是分析多目标问题常用的方法，它的基本思想是根据各自目标问题的重要程度分别乘以一个权系数，相加得到综合评价函数，权系数根据最优化理论中的α法求得。同时在多目标函数加权过程中，当各目标函数值不在同一数量级时，要对各个目标函数值先作量纲为1处理，使其处于等量级，然后进行加权。

本文中所采用的量纲为1处理方法是最优化理论中的极差变换法，见式（20）。

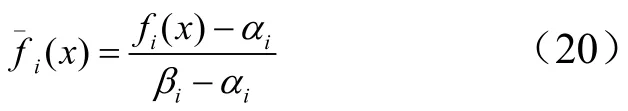
（1）系统经济性目标函数ECO为了分析基液氨浓度变化过程中换热器经济参数AP和汽轮机尺寸参数TP相互作用对系统经济性产生的综合影响，通过线性加权法得出经济性综合评价函数ECO如式（21）所示，ECO越小，系统经济性越好。

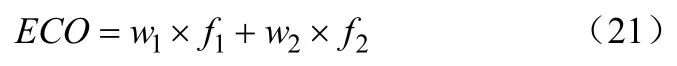
式中，f1为AP经量纲为1处理后的函数值；f2为TP经量纲为1处理后的函数值；w1和w2分别为f1和f2的权系数。根据α法[12-13]求得两个优化目标的权系数，如式（22）、式（23）。

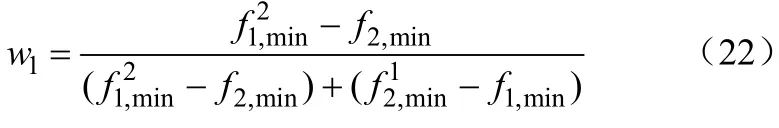
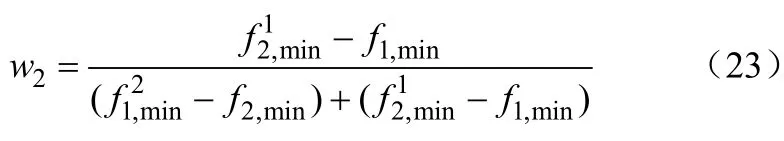
（2）综合目标函数Obj为了分析基液氨浓度对系统经济性和热效率综合性能的影响，对系统经济性目标函数ECO与热效率ef采用线性加权和法进行分析。因为经济性目标函数ECO为越小越好，而系统中热效率应该越大越好，最优化理论中通常以最小值作为最优值。为了使二者加权过程中变化一致，对热效率取倒数处理L=1/ef。对L和ECO进行加权得到综合目标函数如式（24）所示，Obj越小，系统综合性能越好。

式中，g1为L经量纲为1处理后的函数值；g2为ECO经量纲为1处理后的函数值；v1和v2分别为g1和g2的权系数。

根据α法[12-13]求得两个优化目标的权系数，如式（25）、式（26）。

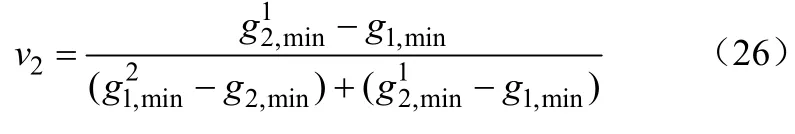
计算过程中，本文通过Matlab R2011a 编写卡琳娜循环系统（KCS34）的热力计算程序，计算过程中各状态点的热力学参数通过调用Refprop8.0实现。Refopr8.0软件的计算模型在温度为250～400K、压力上限为30MPa的范围内，二元混合工质的密度精度可以达到±0.1%[14]。

2 计算结果分析

本文主要对汽轮机入口压力P1分别为1.5MPa、2MPa、2.5MPa时，基液浓度a对各目标参数的影响进行讨论。

2.1 基液氨浓度对系统热效率的影响

图2描述了系统热效率随基液浓度的变化关系。从图2中可以看出，汽轮机进口压力P1一定时，在其可取到的基液氨浓度范围内，系统热效率ef先增大后减小，存在一个最佳浓度使效率达到最大（1.5MPa对应其值为0.5，2MPa对应其值为0.58，2.5MPa对应其值为0.72）。这主要是因为在本文所讨论工况下，热源供热量一定，而在影响系统净输出功因素中泵功相对于膨胀功要小的多，且泵功的变化相对膨胀功变化也很小，所以影响系统热效率的因素主要集中在膨胀功的变化上，即进入汽轮机的富氨蒸汽质量流量qm,v和汽轮机进出口比焓降Δh决定了热效率ef的变化规律。当汽轮机入口压力一定时，基液氨浓度a越大，富氨蒸汽越容易析出，使qm,v越大（图3）。同时当P1一定时，随着基液 氨浓度a增大，冷凝压力增大，汽轮机出口压力增大，使汽轮机进出口比焓降Δh减小（图4）。由于Δh与qm,v随基液氨浓度增大，其变化趋势相反，二者相互作用使热效率先增大后减小。从图2还可以看出，汽轮机入口压力P1越大，热效率的下降段越缓慢，当P1为2.5MPa时，其热效率变化很小。说明压力越高时，基液氨浓度越高对系统热效率影响越小。

图2 基液氨浓度对系统热效率的影响

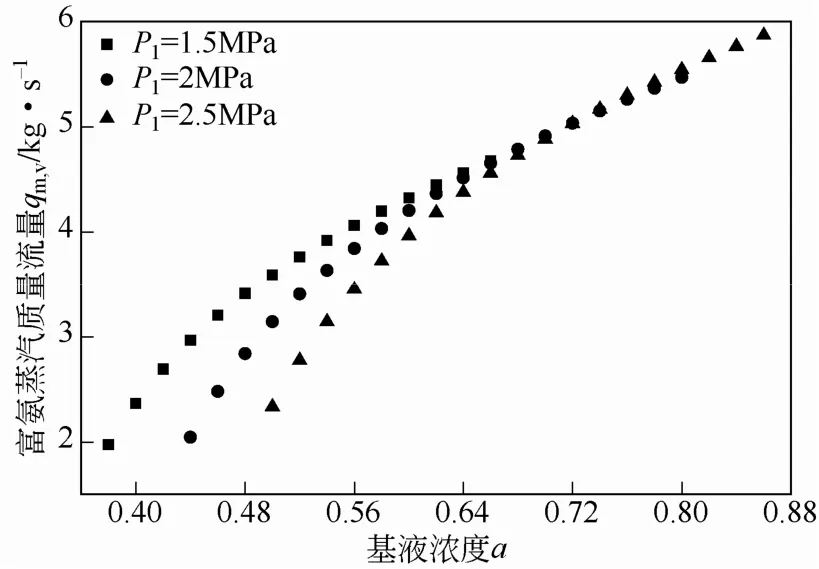
图3 基液氨浓度与富氨蒸汽质量流量的关系

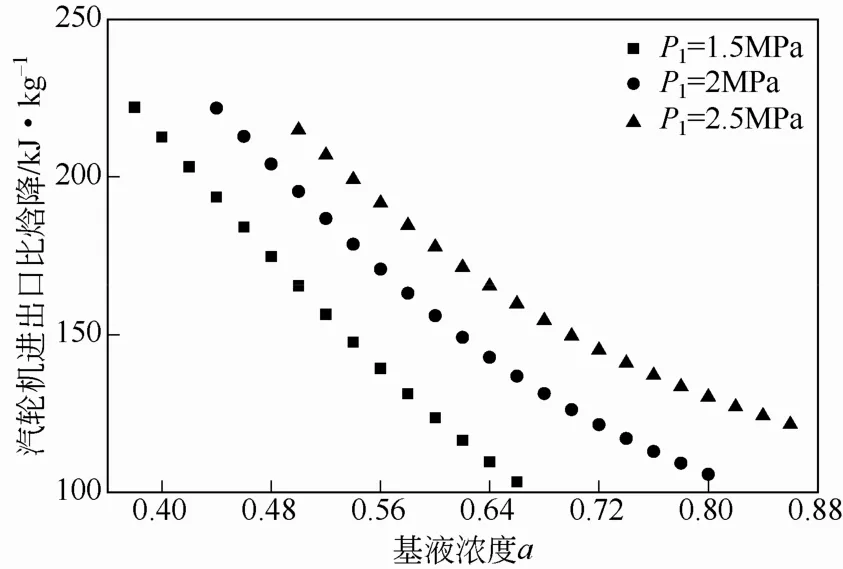
图4 基液氨浓度与汽轮机比焓降的关系

2.2 基液氨浓度对换热器经济参数AP的影响

图5 描述了换热器经济参数AP随基液氨浓度的变化关系，从图5中可以看出，P1一定时，随着基液氨浓度增大，换热器经济参数AP先减小后增大，在某一浓度达到最小值（1.5MPa对应其值为0.52，2MPa对应其值为0.64，2.5MPa对应其值为0.76），即分别在此浓度下，换热器的经济性最好。这主要是因为汽轮机进口压力P1一定时，随着基液氨浓度a增大，系统基液流量qm,b逐渐减小（图6），所以4个换热器的总换热负荷逐渐减小，同时在P1一定时，随基液氨浓度a增大，系统净输出功先增大后减小，所以换热器经济参数AP先减小后增大。同时从图5中还可看出，汽轮机入口压力P1越大， 其上升段的变化逐渐减小，这说明高压力下，基液氨浓度越大其对换热器经济参数影响越小。

图5 基液氨浓度对换热器经济参数的影响

图6 基液氨浓度对基液质量流量的影响

2.3 基液氨浓度对汽轮机尺寸参数TP的影响

图7描述了不同压力下汽轮机尺寸参数TP随基液氨浓度的变化关系。从图7中可以看出，随着基液氨浓度a的增大，汽轮机尺寸参数TP逐渐增大，即在a取最小值时，汽轮机最经济。参数TP出现这种趋势的主要原因是随着a增大，进入汽轮机的富氨蒸汽质量流量qm,v逐渐增大而引起的。同时从图7中可以看出3条曲线均有拐点出现（P1为1.5MPa、2MPa、2.5MPa时其拐点分别在0.46、0.54、 0.64处取得），拐点的出现可以根据式（19）分析得出，当压力P1一定时，随基液氨浓度a增大，冷凝压力增大，使汽轮机出口压力P2逐渐增大，导致出口密度d2逐渐增大。从图8可以看出，随a增大，d2的变化呈线性增加趋势。同时随a增大，进入汽轮机的富氨蒸汽质量流量qm,v逐渐增大，但其增大速度缓慢（图3），d2与qm,v相互作用，使汽轮机出口工质体积流量qv2=qm,v/d2随a的变化呈如图9的变化趋势。即随a增大，qv2先增大后减小，qv2存在最大值，所以TP在qv2最大值处出现拐点；同时由于a增大，汽轮机进出口比焓降Δh减小，使得汽轮机尺寸参数TP呈现整体增长趋势，只是在qv2减小时，TP增加率减小。

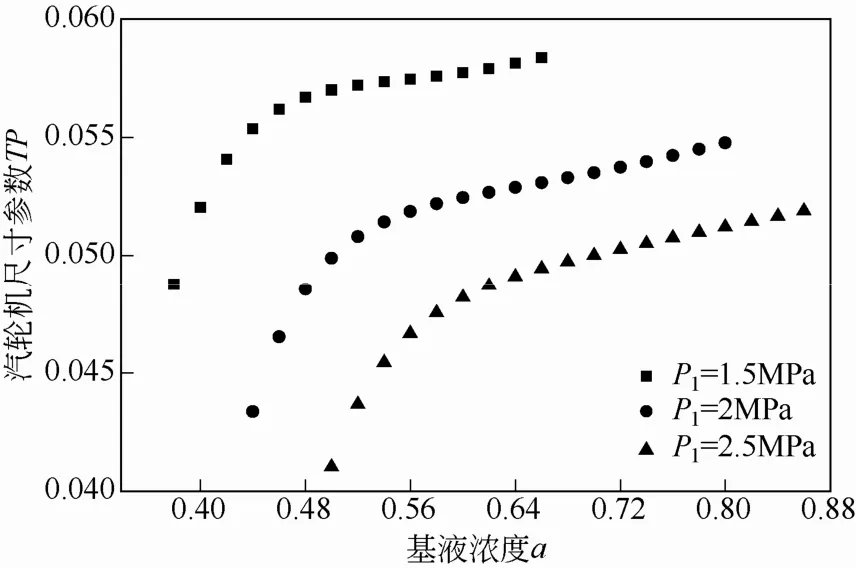
图7 基液氨浓度对汽轮机尺寸参数的影响

2.4 基液氨浓度对系统经济性的影响

图10描述了系统经济性目标函数ECO随基液氨浓度的变化曲线。从图10中可以看出，压力一定时，随基液氨浓度增大，经济性目标函数ECO先减小后增大，并在某一浓度取得最小值（P1为1.5MPa、2MPa、2.5MPa时所对应浓度为分别为0.4、0.48、0.56），即此时系统的经济性能达到最优。同时图10还表明基液氨浓度在一定范围内（即P1为1.5MPa、 2MPa、2.5MPa时所对应浓度范围为分别为0.4～0.5、0.46～0.56、0.54～0.64），目标函数ECO的变化率较小，在此浓度范围内有利于系统的经济性；而当基液氨浓度大于该浓度范围时，经济性目标函数ECO增长率很大，说明较高的基液氨浓度不利于系统的经济性。

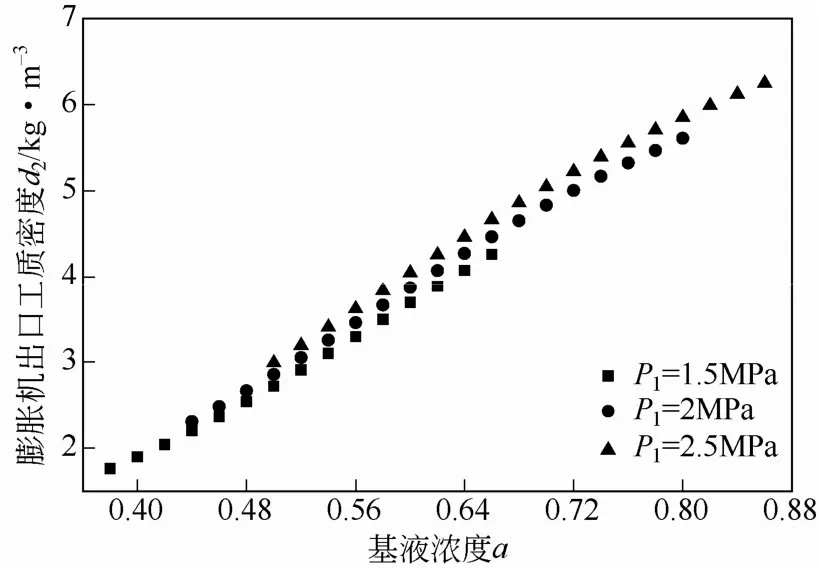
图8 基液氨浓度与汽轮机出口工质密度的关系

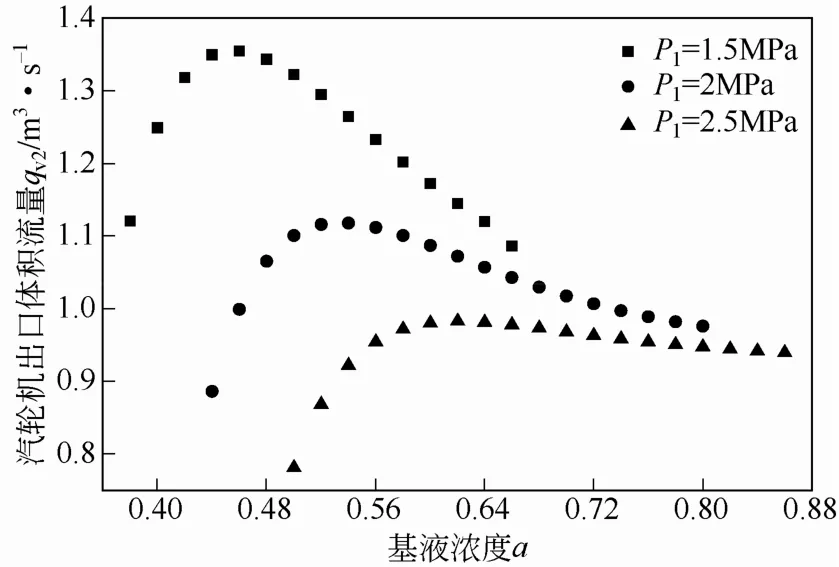
图9 基液氨浓度与汽轮机出口体积流量的关系

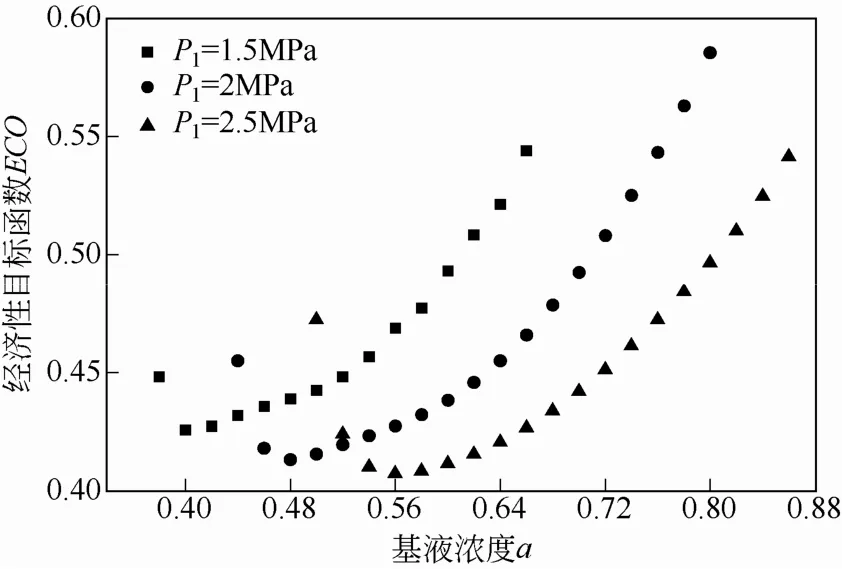
图10 基液氨浓度对经济性目标函数ECO的影响

2.5 基液氨浓度对系统综合性能的影响

图11描述了系统综合目标函数Obj随基液氨浓度a的变化关系。从图11可以看出，汽轮机进口压力P1一定时，Obj随基液氨浓度的增大先减小后增大，存在一个最佳浓度使系统综合性能最优（P1为1.5MPa、2MPa、2.5MPa时所对应浓度为分别为0.44、0.52、0.62）。同时图11还表明，基液氨浓度在一定范围内（即P1为1.5MPa、2MPa、2.5MPa时所对应浓度范围为分别为0.42～0.48、0.48～0.58、0.58～0.68），综合目标函数Obj的变化率较小，在此浓度范围内有利于系统的综合性能。

2.6 系统各目标参数的对比分析

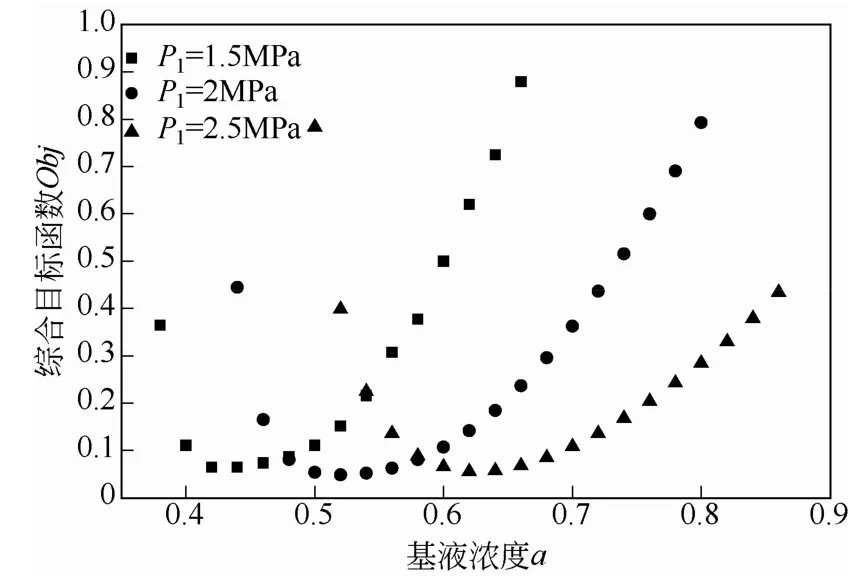
图11 基液氨浓度对综合目标函数Obj的影响

表1 不同目标函数所对应的最佳基液氨浓度

表1给出了汽轮机入口压力P1分别1.5MPa、2MPa、2.5MPa时各目标参数达到最优时所对应的浓度。从表1中可以看出，随着压力P1增大，各目标参数对应的浓度越大；同时表明经济性目标参数ECO最优对应的浓度aECO介于两个子经济参数aAP与aTP之间，综合目标函数Obj最优时所对应的浓度aObj介于两个子参数aECO与aef之间。且压力一定时，各目标最优时所对应最佳浓度的关系为aTP＜aECO＜aObj＜aef＜aAP，同时压力越大，其所对应最佳浓度越大。

3 结 论

（1）以不同目标参数作为系统评价指标时，所对应的最佳基液氨浓度不同。

（2）在单目标性能参数中，基液氨浓度与各目标参数之间存在最佳值，在本文计算条件下，当汽轮机入口压力分别为1.5MPa、2MPa和2.5MPa时，热效率最优时所对应的基液氨浓度分别为0.5、0.58和0.72，换热器性能最优时所对应的基液氨浓度分别为0.52、0.64和0.76，汽轮机尺寸参数最优时所对应的基液氨浓度分别为0.38、0.44和0.5。

（3）对于多目标性能参数，当汽轮机入口压力分别为1.5MPa、2MPa和2.5MPa时，基液氨浓度分别为0.4、0.48、0.56，系统经济性最优；系统的综合性能最优时基液氨浓度分别为0.44、0.52、0.62。

（4）压力一定，各目标参数最优时所对应的最佳浓度的关系为aTP＜aECO＜aObj＜aef＜aAP，同时压力越大，其所对应最佳浓度越大。

符 号 说 明

[1] Wang Jiangfeng，Yan Zhequan，Wang Man，et al. Thermodynamic analysis and optimization of an ammonia-water power system with LNG (liquefied natural gas) as its heat sink[J].Energy，2013，50：513-522.

[2] Thorin E，Dejfors C，Svedberg G. Thermodynamic properties of ammonia-water mixtures for power cycles[J].International Journal of Thermophysics，1998，19（2）：501-510.

[3] Thorin E. Comparison of correlations for predicting thermodynamic properties of ammonia-water mixtures[J].International Journal of Thermophysics，2000，21（4）：853-870.

[4] Fu Wencheng，Zhu Jialing，Zhang Wei，et al. Performance evaluation of Kalina cycle subsystem on geothermal power generation in the oilfield[J].Applied Thermal Engineering，2013，54（2）：497-506.

[5] 何嘉城，郑朝. Kalina 循环34（KCS34）的热力学分析[C]//2012年中国工程热物理学会学术会议论文集，2012.

[6] Wang Jiangfeng，Yan Zhequan，Zhou Enmin，et al. Parametric analysis and optimization of a Kalina cycle driven by solar energy[J].Applied Thermal Engineering，2013，50（1）：408-415.

[7] Campos Rodríguez C E，Escobar Palacio J C，Venturini O J，et al. Exergetic and economic comparison of ORC and Kalina cycle for low temperature enhanced geothermal system in Brazil[J].Applied Thermal Engineering，2013，52（1）：109-119.

[8] Bombarda P，Invernizzi C M，Pietra C. Heat recovery from diesel engines：A thermodynamic comparison between Kalina and ORC cycles[J].Applied Thermal Engineering，2010，30（2）：212-219.

[9] Arslan O. Exergoeconomic evaluation of electricity generation by the medium temperature geothermal resources，using a Kalina cycle：Simav case study[J].International Journal of Thermal Sciences，2010，49（9）：1866-1873.

[10] 任慧琴，李惟毅，张军朋. 低基液氨质量分数对卡琳娜循环系统 （kcs-34） 理论循环效率的影响[J]. 机械工程学报，2013，48（24）：152-157.

[11] Macchi E，Perdichizzi A. Efficiency prediction for axial-flow turbines operating with nonconventional fluids[J].Journal of Engineering for Gas Turbines and Power，1981，103（4）：718-724.

[12] 高雷阜. 最优化理论与方法[M]. 沈阳：东北大学出版社，2005：197.

[13] 王志奇，周乃君，夏小霞，等. 有机朗肯循环发电系统的多目标参数优化[J]. 化工学报，2013，64（5）：1710-1716.

[14] Lemmon E W，Mclinden M O，Huber M L.NIST Reference Fluid Thermodynamic and Transport Properties-REFPROP，Version 8.0[M]. Maryland：National Institute of Standard Technology，2002.