小波去噪中噪声估计失真判别方法

王　新，王建顺

（河南理工大学　电气工程与自动化学院，河南　焦作454000）

小波去噪中噪声估计失真判别方法

王新，王建顺

（河南理工大学电气工程与自动化学院，河南焦作454000）

研究小波阈值去噪时存在的噪声估计失真问题。当采用常见的阈值确定方法对含有较强高频分量的信号进行小波去噪时，小波分析的频带能量泄漏现象会导致噪声估计失真，从而使小波阈值去噪出现较大的偏差。从小波分解的d1细节层和d2细节层的相关性角度，揭示d2细节层频带能量泄漏对噪声估计影响的规律，提出根据d1、d2细节层的最大相关系数判别噪声估计失真的方法。最后，给出解决噪声估计失真的方法。实验表明，该方法可以很好地判别小波去噪中是否出现噪声估计失真，可以避免出现去噪后信号有用信息损失严重的问题。

声学；小波去噪；噪声估计失真；阈值方法；频带能量泄漏

小波去噪是一种先进的去噪方法。小波阈值去噪法是小波去噪方法中应用较广泛的一种方法，其去噪过程包括小波分解、去噪处理和小波重建三大步骤，其中去噪处理过程中的阈值确定方法是小波去噪的关键。常见的阈值确定方法有如下四种：长度对数阈值法（即sqtwolog）、基于Stein的无偏似然估计（SURE）阈值法（即rigrsure）、启发式SURE阈值法（即heursure）和极小极大方差阈值法（即minimaxi）［1，2］。由于阈值确定方法与噪声估计有着紧密地联系，所以噪声估计的准确性是小波去噪的关键。

由于噪声估计一般是以小波分解的最高频率频带（即d1细节层，以下简称d1层）的小波系数进行估计的［3］，所以当信号本身存在一定程度的高频分量时（这些高频分量不是噪声信号），将会对噪声估计产生影响。若有高频分量处于d1层频带，则肯定会对该层的小波系数以及噪声估计产生显著的影响。因此，小波去噪时一般都会尽量避免高频分量处于d1层频带。但是，往往会忽视处于最高频率频带的相邻频带（即d2细节层，以下简称d2层）的高频分量对噪声估计的影响。在实际系统中，因测量条件及其它因素所限，采样频率不宜过高，信号可能存在处于d2层的高频分量的现象。关键是处于d2层的高频分量是否会引起噪声估计的失真。由于噪声估计失真通常使噪声估计远大于真实值，从而导致信号小波去噪后有用信息损失严重，对小波去噪效果有恶劣影响，所以判别噪声估计是否失真非常重要。小波分析存在频带能量泄漏现象，该问题在许多文献中已有探讨［4-6］。但是，频带能量泄漏现象对小波去噪影响的研究还不够成熟，缺乏频带能量泄漏对噪声估计的影响定量分析，尤其缺乏判别噪声估计是否出现失真的方法。

为此，本文重点研究d2层中高频分量的频带能量泄漏对噪声估计和小波去噪效果的影响。主要成果在于从d1层和d2层小波系数的相关性角度，分析频带能量泄漏对噪声估计影响的程度，提出噪声估计失真的判别方法，并提出噪声估计失真情况下的解决方法。

1　小波阈值去噪方法与噪声估计

在小波阈值去噪过程中，去噪处理环节包括两个步骤：一是根据阈值的确定方法计算阈值，二是根据该阈值采用作用阈值方法进行处理。

1.1阈值的确定方法

阈值的确定方法是小波去噪效果好坏的关键之一。常见的阈值确定方法有如下四种：sqtwolog、rigrsure、heursure和minimaxi，上述方法在MATLAB中也有介绍。其中sqtwolog方法和minimaxi方法与噪声估计的关系最为直观。例如，sqtwolog法的阈值计算公式为式中为噪声估计，N为d1层小波系数的个数。λ作为小波分析的各细节层的阈值［7-10］。本文以sqtwolog法为例进行分析。

1.2作用阈值方法

作用阈值方法主要有硬阈值法和软阈值法，此外还有一些改进方法。由于软阈值法去噪后信号的小波系数在阈值λ处的连续性好于硬阈值法，所以软阈值法更为常用。在作用阈值处理过程中，采用软阈值法对小波系数进行处理后，得到的小波系数为

式中λ为阈值。以下分析采用的作用阈值方法均为软阈值法［7-10］。

1.3基于小波系数的噪声估计

一维含噪信号的模型可表示为

式中s（x）为观测得到的含噪信号，f（x）为有用信号，n（x）噪声信号，假定n（x）是服从的高斯白噪声。

白噪声n（x）的小波变换为

式中ψa（x）是尺度为a的小波函数。

因为

由此可见，白噪声信号的||Wa（a，x）2的均值与尺度a成反比。随着尺度的增大，白噪声的小波变换系数是逐渐减小的。因此，通常情况下认为信号主要集中在小波变换的低频频带，而噪声主要集中在小波变换的高频频带，并且可以由此来估计噪声的方差。利用小波系数进行噪声估计的常见方法为

所以

1.4噪声估计失真的影响

由式（1）可知，当d1层小波系数的个数N一定时，sqtwolog法的阈值只与噪声估计σ^有关，一旦出现噪声估计失真，必然影响去噪效果。由式（8）可知，噪声估计取决于d1层的小波系数，噪声估计的前提条件是该层的小波系数只含噪声信息。如果按照采样定理来确定采样频率时，使d1层频带只含噪声信息，而不包含有用高频分量，那么理论上可以满足噪声估计的前提条件。

但是，在实际情况下，d1层的小波系数还可能包含来自d2层高频分量的频带能量泄漏。通常情况下，d2层频带能量泄漏会导致噪声估计失真，σ^会比实际值大，从而导致去噪阈值偏大，去噪后信号中有用信息出现损失。下面定量分析频带能量泄漏对噪声估计的影响，判断是否达到噪声估计失真的程度。

2　频带能量泄漏对噪声估计的影响

2.1实验方法

为了定量分析频带能量泄漏对噪声估计的影响，构造信号如下

2.2频带能量泄漏对噪声估计的影响

由前面的分析和式（8）可以看出，N一定时噪声估计只与d1层的小波系数紧密相关。由于信号）的

f1、f2、f3分量和分量都不处于d1层。所以，在理想情况下，可以认为其噪声估计与这四个频率分量无关，信号）的噪声估计是相同的。但是，实际情况下却不是这样。

由于小波分析存在频带能量泄漏，x2（k）相对x1（k）而言，d1层的小波系数包含该层噪声和f4分量在该层的能量泄漏两种信息，前者是固有计算噪声估计的依据，而后者对噪声估计有一定的影响，是不希望有的因素。为了定量观察f4分量对噪声估计的影响，假定表示x2（k）的噪声估计与的噪声估计之比。这样，可以观察不同信噪比下变化对的影响，与的关系曲线如图1所示。

可见，f4分量在d1层的能量泄漏信息会使噪声估计增大，出现噪声估计失真，并且基本上噪声估计失真程度随f4频率值的增大而增大。对于同样频率的f4分量，信噪比SNR越大，f4分量对噪声估计的影响越大。噪声估计失真会使信号去噪后的有用信息损失严重，对小波去噪有恶劣影响。

因此，在小波去噪过程中，判断噪声估计是否失真是小波去噪的关键。

3　噪声估计失真的判别方法

3.1最大相关系数计算方法

首先将信号做归一化处理，然后进行小波分解并单支重构，得到重构后的d1、d2层小波系数，分别为Wf（J，k）和Wf（J-1，k），这里J为小波分解的层数，为单支重构后d1、d2层的点的个数）。根据Wf（J，k）和Wf（J-1，k），可以直接求其相关系数R（n），即［11］

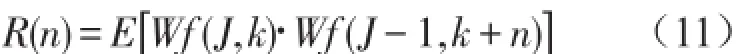
改变n，可以改变d1、d2层的小波系数的相关系数。假定n=τ（0≤τ≤M1）时，相关系数R（n）最大，即R（τ）为R（n）的最大值。

3.2基于最大相关系数的噪声估计失真判别方法

通过实验仿真，可以得到信号x2（k）在不同信噪比下Δf4与R（τ）的关系，如图2所示。由图2可知，在同一Δf4下，R（τ）与信噪比SNR有关，SNR越大，R（τ）越大；在同一信噪比SNR下，R（τ）与Δf4近似成线性关系。

以上分析是在f4分量的幅值U4为3 V不变情况下，得到的和R（τ）随Δf4变化的规律。同理，在f4分量频率不变情况下，也可以得到和随幅值U4变化的规律。由于在f4频率相同情况下，U4增大，信号x2（k）归一化处理后，f4分量在信号x2（k）中占的份量增大，所以和R（τ）基本上随U4增大而增大。因篇幅所限，这里不再赘述。

鉴于以上特点，噪声估计失真的判别准则为：若R（τ）≥ε，则噪声估计失真；反之，则噪声估计正确。这里，ε为一个阈值。

由于Δf4接近0时，信号x2（k）的f4分量在d1层的能量泄漏信息非常弱，对噪声估计和最大相关系数R（τ）影响非常小。此时，信号x2（k）的最大相关系数R（τ）与信号x1（k）相接近。大量实验发现，由于白噪声具有随机性，所以程序每次运行得到的R（τ）值不是定值，而是在一定范围内变化的。在信噪比SNR=15～30情况下，信号x1（k）的R（τ）变化范围为0～0.08。因此，可以参考该R（τ）变化范围选择判断噪声估计是否失真的阈值ε。

考虑d1层非噪声微弱频率分量和信噪比的影响，ε的取值可略做调整，一般取0.08≤ε≤0.1。

综上所述，噪声估计失真的判别方法及步骤如下：

（1）将待去噪信号作归一化处理；

（2）将归一化处理后的信号进行小波分解和单支重构，得到d1、d2层的小波系数Wf（J，k）和Wf（J-1，k）；

（3）根据Wf（J，k）和Wf（J-1，k），计算其最大相关系数R（τ）；

（4）确定ε的值，然后根据噪声估计失真的判别准则确定是否存在噪声估计失真。

3.3噪声估计失真的处理方法

图1　σ^r与Δf4的关系曲线

当噪声估计失真出现时，不能根据原有的噪声估计值进行小波去噪分析，需要采取措施使噪声估计不再失真。从图1可知，频率为f4的分量越远离d1层频带，其频带能量泄漏对σ^的影响越小。由于增加采样频率和小波分析的层数，可以使频率为f4的分量远离d1层频带，从而减弱频带能量泄漏对σ^的影响。所以，适当增大采样频率可以避免出现噪声估计失真的现象。

鉴于此，在对实际信号进行小波阈值去噪处理过程中，在满足采样定理要求情况下，采样频率的确定还要考虑避免出现噪声估计失真的现象。

4　实例分析

为了验证上述方法的效果，下面以交-交变频调速系统输出电流为例进行分析。为了比较不同采样频率fs的分析效果，这里fs分别取2 500 Hz和5 000 Hz，采样点个数为2 048。在小波分析中，仍选择Daubechies 3小波，层数为4层。这样，小波分解各细节层对应的频带频率范围如表1所示。

表1　频带频率范围

图2　R（τ）与Δf4的关系曲线

fs=2 500 Hz时采集到的交-交变频器输出电流波形如图3所示，其对应的幅值谱如图4所示，为了观察方便，图中数据均做了归一化处理。

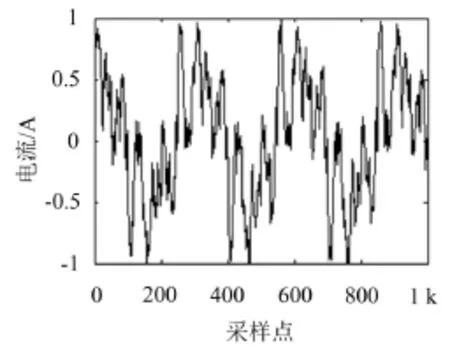
图3　输出电流波形

图4　输出电流频谱

由图4可以看出，交—交变频器的输出电流谐波成分丰富含量较高，其中对应的小波分解d2层频带含有一定的谐波成分，对噪声估计有一定的影响。根据本文提出的方法得到d1、d2层小波系数的最大相关系数R（τ）=0.312 2，根据噪声估计失真的判别准则，此时做噪声估计将会失真。为此，将采样频率提高为fs=5 000 Hz，这样fs=2 500 Hz下的d2层频带变为fs=5 000 Hz下的d3层频带，此时得到d1、d2层小波系数的最大相关系数R（τ）=0.0721。可见，提高采样频率后，可以避免出现噪声估计失真的现象。

5　结语

（1）由于小波分析存在频带能量泄漏影响，所以运用常见的阈值确定方法，对含有较强高频分量的信号进行小波去噪时，信号中处于d2层的高频分量对小波去噪的噪声估计有较大的影响。它导致噪声估计失真，出现噪声估计值比实际值大许多的现象，而且高频分量的频率越接近d2层频带上限，其影响越大。噪声估计失真会导致小波去噪后信号有用信息损失严重，产生不良的后果；

（2）通过小波单支重构后d1、d2层的小波系数的最大相关系数分析，可以判断噪声估计是否出现失真现象。当出现噪声估计失真时，可以通过提高采样频率的方法排除d2层频率分量能量泄漏的影响，达到小波去噪后信号有用信息无严重损失的目的。

［1］Donoho D.L.De-noising by soft-thresholding［J］，IEEE Transactions on Information Theory，l995，41（3）:6l3-627.

［2］肖方煜，汤伟，傅娜.自寻优阈值小波去噪方法［J］.信号处理，2012，28（6）：577-586.

［3］曲巍崴，高峰.基于噪声方差估计的小波阈值降噪研究［J］.机械工程学报，2010，45（2）：28-33.

［4］王新，林家骏.小波分析中频带能量泄漏及对策研究［J］.辽宁工程技术大学学报，2005，24（5）：734-736.

［5］张君，韩璞，董泽，等.基于小波变换的振动信号分析中能量泄漏的研究［J］.中国电机工程学报，2004，24（10）：238-243.

［6］Peng Z K，Jackson M R，Rongong J A，et al.On the energy leakage of discrete wavelet transform［J］.Mechanical Systems and Signal Processing，2009，23（2）:330-343.

［7］王新，朱高中.一种新型小波阈值法在信号消噪中的应用研究［J］.高电压技术，2008，34（2）：342-345.

［8］代海波，单锐，王换鹏，等.基于改进阈值函数的小波去噪算法研究［J］.噪声与振动控制，2012，32（6）：189-193.

［9］王宏强，尚春阳，高瑞鹏，等.基于小波系数变换的小波阈值去噪算法改进［J］.振动与冲击，2011，30（10）：165-168.

［10］苏成志，陈洪印，孟凡一，等.新阈值二进小波去噪算法在齿轮信号中的应用［J］.计算机工程与应用，2014，50 （18）：206-209.

［11］邓禹，熊静琪，孙锐，等.利用相关原理优化小波阈值去噪［J］.噪声与振动控制，2009，29（1）：61-64.

Identification Method for Noise Estimation Distortion in Wavelet Denoising

WANGXin，WANG Jian-shun
（School of Electrical Engineering andAutomation，Henan Polytechnic University，Jiaozuo 454000，Henan China）

When the signals containing some high frequency components are denoised by using the wavelet denoising with conventional threshold selection methods，the frequency-band energy leakage in wavelet analysis will lead to the distortion of the noise estimation，so that the wavelet threshold denoising may contain large errors.In this paper，the noise estimation distortion in the wavelet threshold denoising was studied.In view of the relevance between the d1 detail level and the d2 detail level，the influence of the frequency-band energy leakage of the d2 detail level on the noise estimation was analyzed.The identification method for noise estimation distortion was proposed by using the maximum correlation coefficient of the d1 detail level and the d2 detail level.Finally，the method of restraining the noise estimation distortion was given.The results of test show that the noise estimation distortion can be distinguished by using this method，and the trouble of the useful information missing in the wavelet denoising process can be avoided.

acoustics；wavelet denoising；noise estimate distortion；threshold method；frequency band energy leakage

TN911.7

ADOI编码：10.3969/j.issn.1006-1335.2015.05.030

1006-1355（2015）05-0145-05+173

2015－01－30

国家自然科学基金项目（61403129）；河南省科技攻关项目（142102210048）

王新（1967－），男，河南省卢氏人。博士，教授，博士研究生导师，主要研究方向为状态检测与故障诊断、电气传动和智能仪器仪表等。

E-mail:wangxin@hpu.edu.cn

王建顺（1988－），男，河南兰考人。硕士研究生，主要研究方向为信号处理。

E-mail:wangjs8804@163.com