基于北斗数据的非差相对定位理论与方法研究

邵珍珍，潘思晓，邵成立，宫宁

(1.青岛市勘察测绘研究院，山东 青岛　266032；2.青岛市国土资源和房屋管理局，山东 青岛　266002)



基于北斗数据的非差相对定位理论与方法研究

邵珍珍1，潘思晓2，邵成立1，宫宁1

(1.青岛市勘察测绘研究院，山东 青岛266032；2.青岛市国土资源和房屋管理局，山东 青岛266002)

简要介绍了北斗导航定位系统，论述了非差相对定位的基本概念、原理及建立非差相对定位模型的基本原则，介绍了建立单历元非差相对定位模型的函数模型和随机模型的详细过程，利用LAMBDA方法实现基线单历元模糊度的固定。对单历元非差相对定位的基线解算精度进行了重点分析。

北斗导航定位系统；非差相对定位；参数重整

引文格式：邵珍珍，潘思晓，邵成立，等.基本北斗数据的非差相对定位理论与方法研究[J].山东国土资源，2015，31(9)：57-62.SHAO Zhenzhen, PAN Sixiao, SHAO Chengli,etc.Research on the Theory and Method of Un-differenced Relative Positioning Based on Beidou Data[J].Shandong Land and Resources,2015，31(9)：57-62.

北斗系统是中国正在实施的自主发展、独立运行的全球卫星导航系统，至2012年，北斗已按照其发展运营计划具备了对亚太地区提供无源定位、导航、授时服务的能力，基于北斗导航系统的服务应用能力以及战略意义，国内外对北斗的研究正大范围展开；目前GNSS高精度定位中双差模型使用最为广泛，但是其自身也存在缺点。非差精密定位因为其观测值利用率高、观测值之间不存在相关性等等优点也一直是卫星导航定位的研究热点。但是利用非差模型进行相对定位，其模型存在秩亏和模糊度非整数的问题，该文重点阐述解决上述问题的参数重整的方法，构建单历元非差定位的函数模型和随机模型，并进行数据处理及精度分析。

1　北斗导航定位系统简介

北斗系统定位原理虽然与GPS系统基本相同，但其在卫星星座、卫星信号、坐标系统、时间系统上是不同的。并且在系统功能方面，北斗系统除了导航和定位，还具有通信和精密授时的功能。

1.1坐标系统

北斗系统采用的坐标系统为2000中国大地坐标系(China Geodetic Coordinate System 2000,CGCS2000)。该坐标系统与国际地球参考框架(ITRF)保持很高的一致性，差异约为5cm，应用起来非常的方便，不用考虑CGCS2000与ITRF之间的坐标转换。

1.2时间系统

北斗时间系统，简称北斗时(BDT)，是一个连续的时间系统，秒长取国际单位制SI秒，起始历元为2006年1月1日0时0分0秒协调世界时(UTC)。BDT与TAI有33秒的偏差，即TTAI-TBDT=33s；GPS时与ATI时存在一常量偏差：TTAI-TGPS=19s；BDT与GPST之间的转换关系是：TGPS-TBD=14s。

1.3北斗GEO卫星位置计算方法

北斗导航定位系统是由MEO+GEO+IGSO组成的混合星座，MEO和GPS卫星的轨道特征类似，IGSO和GEO卫星轨道特征与MEO不同，MEO与IGSO卫星轨道计算方法与GPS卫星是相似的，但GEO卫星的轨道倾角接近于0，因此其轨道计算与GPS卫星不同。相关文献已经给出适用于北斗GEO卫星的轨道拟合算法——坐标旋转法。

2　非差相对定位关键技术

双差定位模型之所以被广泛利用，是因为其不但消除了大部分误差源的影响，比较好的运用了观测值，还具有较少的待估参数，模型较为简单；最重要的是利用了双差模糊度整数特性。但对观测值之间求差后也存在一定的缺点，如数据的利用率比较低，一些好的数据因为与其配对的数据出现问题而无法使用，数据的利用率随着求差次数的增加而降低，并且双差观测值本身相关包括所有可用的观测值，双差观测值较难相互独立，为质量控制带来困难等。相比而言，非差模型有其自身的优势：无需建立差分观测值，可用的观测值多，保留了所有的观测值信息；观测值之间不存在数学相关，便于质量控制，非差模型更方便模型化误差，误差的绝对信息从待估量中获得，便于对误差的随机特性和物理特性进行研究；在多站的定位中，非差模型更容易选择线性独立的独立基线，并且更易集成不同系统的信号。

2.1参数重整构建单历元非差定位函数模型

以B1波段伪距和载波相位为例，得出非差观测值的线性化方程：

(1)

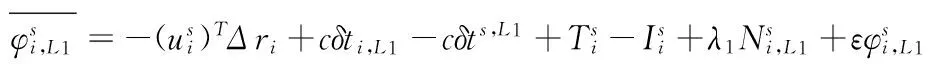
如若考虑2个测站，分别接收到m颗北斗卫星两个波段的载波相位和伪距观测值，按照式子(1)和(2)一共可以列出8m个非差观测值方程。观测值之间不进行差分，要同时估计出所有的参数，就会存在2个问题：一是设计矩阵秩亏，二是模糊度与接收机和卫星初始相位无法分离，不是整数，因此不能以整数的形式求解，应该设法将模糊度表示为双差的形式，才能保证得到高精度的满足需求的定位结果。传统解决秩亏的方法是定义基准(基准个数等于秩亏个数)，对于单历元的北斗观测值，选择合适的解决秩亏的基准并不容易。

2.1.1双差模糊度

(3)

(4)

(5)

将(4)和(5)带入(3)得到：

(6)

从(6)式中可以看出：双差模糊度可以消去初始历元卫星和接收机初始相位影响，还可以消除初始历元接收机和卫星钟差的影响，只剩测站和卫星初始模糊度的互差，因此载波的双差模糊度具有整周的特性。

2.1.2参数重整

利用非差模型进行相对定位时单历元模型的建立，存在着非差模糊度非整数和设计矩阵秩亏的问题，要通过参数重整来解决，根据需求和各参数的特性，先给出参数重整的基本原则：①参数重整只对于参数空间进行重整，观测值保持不变,维持观测值非差的状态；②观测方程左右等量关系维持不变；③感兴趣的需要估计的参数不参与重整，如基线向量；④新整合的接收机钟差项对于每颗卫星是保持不变的；⑤新整合的卫星钟差对不同测站的接收机保持不变；⑥重整后的模糊度是以双差形式存在。

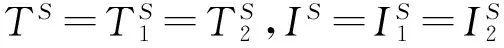
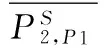
(7)

从式(7)中，可以得到如下信息：经过参数重整之后，P1伪距的观测方程右侧同时增加了一正一负的接收机钟差项cδt1，p1，分别重整了一个新的接收机钟差项dt12，p1和卫星钟差项dts，p1。再将接收机1的P1伪距观测方程做重整，考虑到Δr1=0,重整后的方程为：

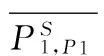
=-(cδts，P1-cδt1，p1-TS-IS)+εp1

=-dts，p1+εp1

(8)

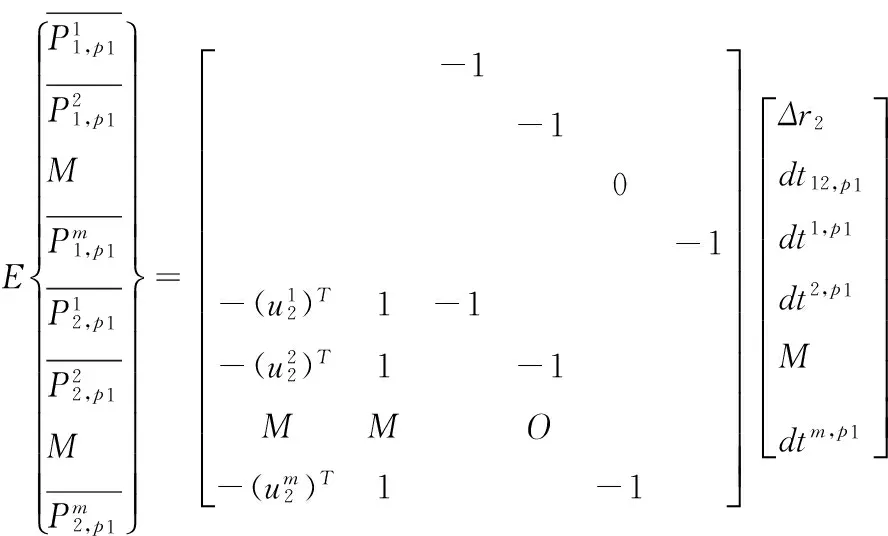
(9)

类似可得两台接收机1和2的P2伪距观测方程的参数整合后的方程。

载波相位较伪距重整参数复杂，因为其存在模糊度参数。因为要将模糊度参数重整为双差的形式。以卫星1为参考卫星，先整合接收机2的B1载波相位的观测方程：

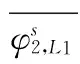
(10)

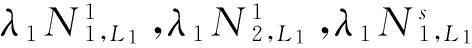
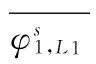
=-dts，L1+εL1

(11)

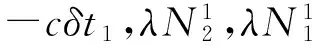
(12)

类似可得B2载波的整合后的观测方程，发现上述重整的观测方程存在的规律性，令

分别表示接收机1和2的非差伪距和载波相位观测值，同理可得另一频率、双差模糊度、带偏差的卫星钟差项的简写符号。令

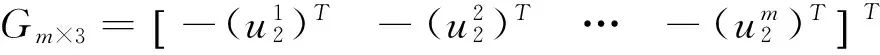
E=(0T，Im-1)T，em为所有元素都是1的m维向量。考虑到2个测站的双频载波和码伪距观测值，就可以得北斗单历元非差相对定位函数模型：

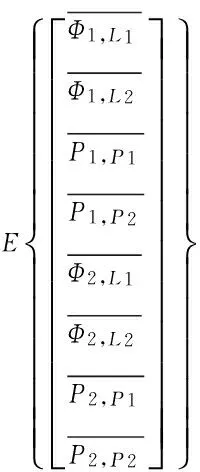
(13)

重整参数后发现，在单历元的情况下，观测到m颗卫星，可以组建8m个非差观测值方程，存在6m+5个未知参数，存在的多余观测数为8m-(6m+5)=2m-5个，设计矩阵不再秩亏，模糊度也重整为双差的形式，并且最少只需要3颗卫星就可以满足定位条件。

2.2单历元非差北斗定位随机模型

考虑接收机1，观测颗北斗卫星，获得个非差B1载波相位的观测值。不考虑星间相关。则(假设处于任何位置的GPS卫星均等精度)：

(14)

(15)

假设2个波段的同类观测值的精度是相等的，不考虑卫星间和接收机间的物理相关，考虑接收机1,2的所有P1，P2和B1，B2载波相位观测值，可以得到参数估计的先验方差-协方差阵简化为：

(16)

式(16)是得到的简化方差-协方差矩阵，是对角阵，不存在数学相关。这样，利用上式的函数模型和随机模型就构成了完整的非差相对定位模型。对于北斗卫星而言，码伪距和载波相位的观测精度差距非常的大，图1与图2为北斗某颗卫星的载波相位和码伪距的观测值残差。

图1　C01号卫星载波相位残差(单位m)

图2　C01号卫星码伪距残差(单位m)

在单历元非差相对定位随机模型构建时，码伪距和载波相位的权重的设置是非常重要的，直接关系到单历元模糊度的固定情况与定位的精度。以一组短基线数据为例，开始将载波相位与测码伪距其权比设置为1000∶1，对于此条短基线解算结果如图3所示。

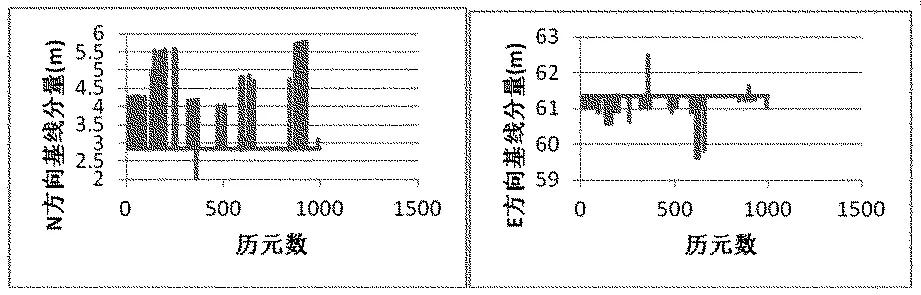
图3　权重1000∶1时基线解算结果

由图3会明显看出，某些历元定位存在着跳动非常大的情况，并且在N，E，U 3个方向的跳动时刻是一致的，产生这种结果的原因就是模糊度固定不正确造成的。因此相应调高载波相位所占的权重，得到的结果如图4所示(以N方向为例)。由图4可以看到，单历元非差相对定位的随机模型的正确建立是非常重要的，直接关系到模糊度的正确固定和定位结果的正确性。

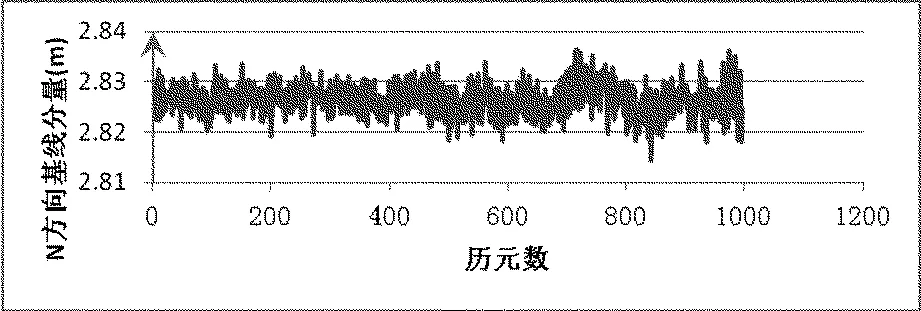
图4　权重调整后的基线解算结果

2.3单历元精密定位的步骤

①对数据进行预处理，剔除粗差并且处理历元缺失等情况；②建立包括伪距和载波相位在内的差分函数模型和随机模型；③运用标准最小二乘法获得模糊度和其他参数的浮点解；④采用LAMBDA方法，通过整数变换和搜索技术将模糊度固定为整数；⑤解算出整周模糊度的前提下，回代到模型中,获得高精度的参数估值。

3　实验分析

为验证上述参数重整方法的正确性，首先使用零基线来进行检验。选用2012年11月12日0点0分—2点30分左右的武汉大学测绘学院四楼采集的北斗双频数据来进行数据处理，采用上述的单历元非差相对定位的模型，并利用LAMBDA方法进行对单历元模糊度进行固定(图5)。

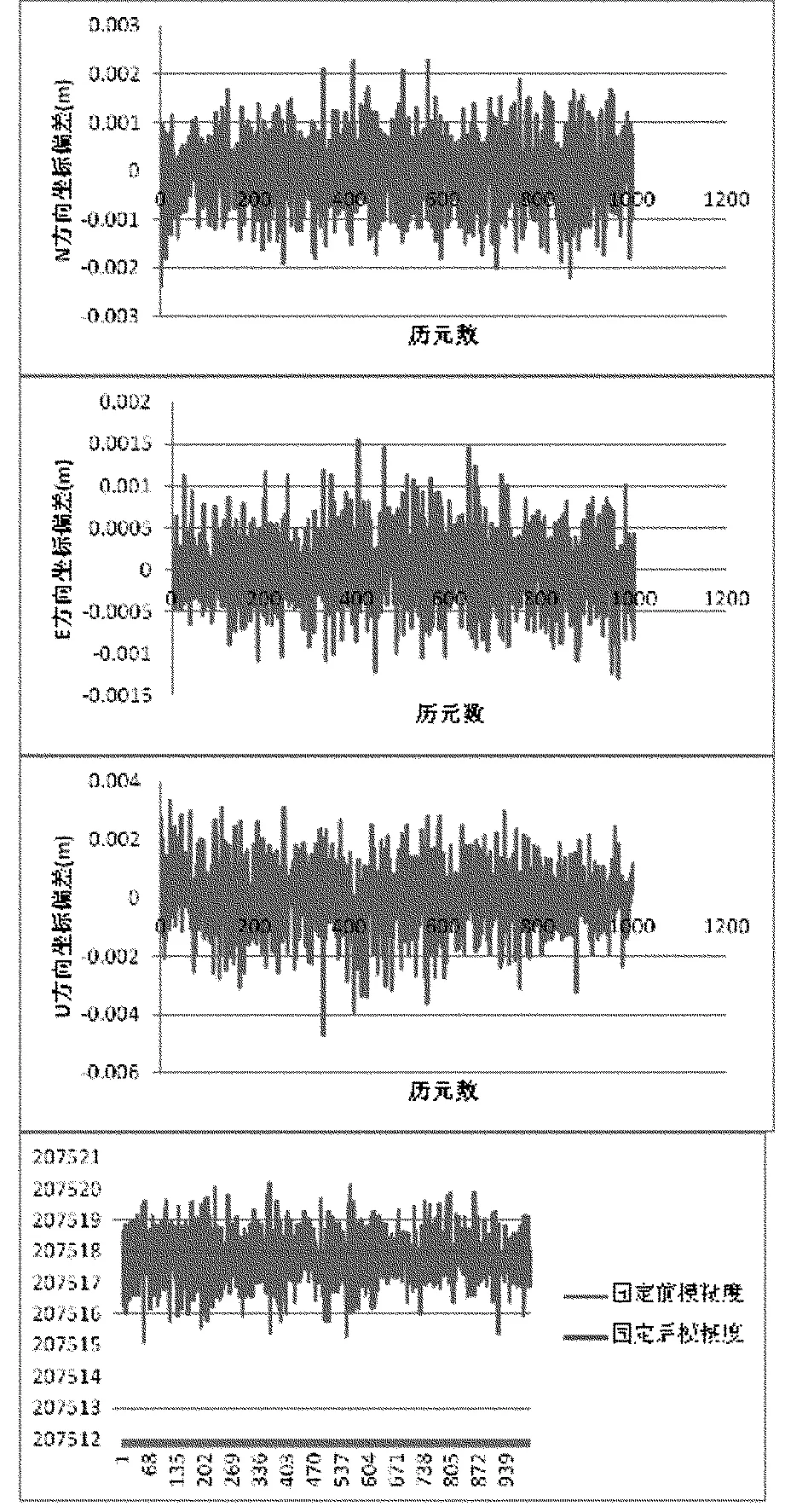
图5　零基线在N,E,U方向的坐标偏差及单历元模糊度固定情况

从图5可以看出，利用非差观测值方程进行相对定位在北和东两个方向均可以达2.5mm之内的精度，而高差方向偏差稍大，大约为0～5mm，与双差定位的精度基本一致；双差模糊度可以正确固定，论证了非差参数重整的并使用LAMBDA方法单历元固定模糊度的可行性。

再以一条短基线为例，来分析算法的定位精度。短基线数据分别采集于武汉大学信息学部校园，通过自己编制的非差相对定位程序来进行短基线解算并进行定位精度分析，并与由商业软件解算出的定位结果进行对比，其坐标偏差如图6所示。

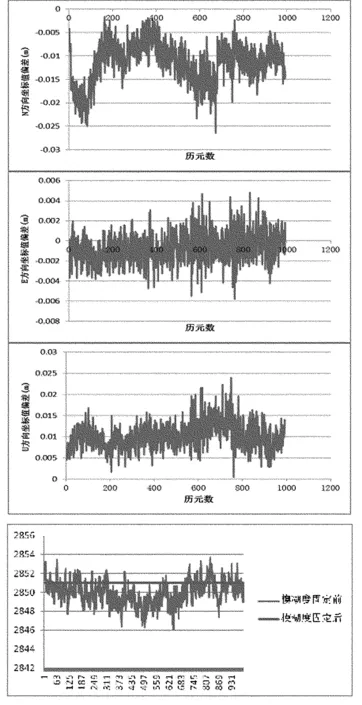
图6　短基线在N，E，U方向的坐标偏差及模糊度固定前后对比

从图5、图6可以看出，使用所论述的方法进行零基线及短基线的解算可以得到较好的解算精度。对于零基线的解算精度在N，E两个方向可以达到2.5mm以内，精度最差的U方向也可以达到5mm以内。对于短基线，N，U两个方向的定位结果在3cm左右，而E方向可以达到5mm以内。这与我国目前北斗二代(亚太地区)卫星分布有关系(表1)。

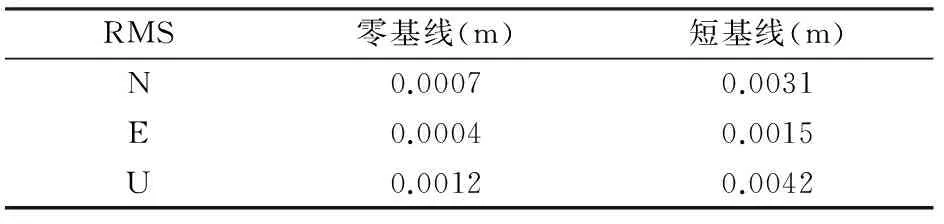
表1　零基线与短基线精度对比

4　结论

经过上面的实例分析和图表证明：参数重整构建单历元非差相对定位模型并利用LAMBDA方法进行单历元模糊度的固定，对短基线解算是有效的，并且具有与双差定位模型相类似的精度。在数据处理过程中，可能考虑的误差模型和随机模型不够精确，会影响定位结果，在以后的工作中，需要进一步精化模型。

对于长基线数据来说，由于误差的影响，单历元进行模糊度的固定可能会存在一定的困难，因此在单历元解算长基线的情况下，要寻求更加有利于模糊度固定的方法，或者先对模糊度进行初始化，再逐历元进行计算。

[1]柳响林,刘经南,王新洲.单历元GPS非差相对定位模型的研究[J].测绘通报，2003，(3)：5-8.

[2]李征航,黄劲松.GPS测量与数据处理[M].武汉：武汉大学出版社，2005.

[3]刘季.北斗GEO卫星位置计算方法探究[J].测绘地理信息，2012，37(5)：34-36.

[4]魏子卿,葛茂荣.GPS相对定位的数学模型[M].北京：测绘出版社，1998.

[5]高星伟,过静珺,程鹏飞,等.基于时空系统统一的北斗与GPS融合定位[J].测绘学报，2012，41(5)：743-748.

Research on the Theory and Method of Un-differenced Relative Positioning Based on Beidou Data

SHAO Zhenzhen1, PAN Sixiao2, SHAO Chengli1, GONG Ning1

(1. Qingdao Surveying and Mapping Institute, Shandong Qingdao 266032, China; 2. Qingdao Land and Resources and the Housing Authority Bureau, Shandong Qingdao 266002, China)

Beidou system has been briefly introduced in this paper, basic concept of un-differenced relative positioning has been discussed, and the principle for establishing un-differenced relative positioning model has been introduced in detail. The detailed process for establishing the function and stochastic model of single epoch un-differenced relative positioning model have been introduced. By using LAMBDA method, single ambiguity fix has been realized. The positioning accuracy of the baseline solution by using single epoch relative model has been analyzed as well.

Beidou navigation system;un-differenced relative positioning; parameters reforming

2015-06-23；

2015-07-10；编辑：曹丽丽

邵珍珍(1990—)，女，山东德州人，助理工程师，主要从事卫星导航定位研究工作；E-mail:shaozhenzhen9999@126.com

P208

B