海杂波背景下的组合自适应GLRT-LTD

刘 明水鹏朗

（西安电子科技大学雷达信号处理国家重点实验室 西安 710071）

海杂波背景下的组合自适应GLRT-LTD

刘 明*水鹏朗

（西安电子科技大学雷达信号处理国家重点实验室 西安 710071）

为了检测海杂波背景下的微弱运动目标，相干检测器通常需要作长时间的累积。然而，长时累积条件下的目标多普勒频率的扩散和幅度的起伏以及海杂波空间非均匀性对参考单元数目的限制导致传统的自适应检测器没法工作。注意到逆伽马（IG）纹理的复合高斯分布（CGD）可以很好地描述海杂波和目标的瞬时频率是时间的慢变函数，该文提出一种组合自适应检测器，即组合自适应广义似然比线性门限检测器（CA-GLRT-LTD），它由自适应GLRT-LTD在几个连续的短的累积间隔上的最大响应的乘积的构成。由于GLRT-LTD对IG纹理的复合高斯杂波的最优性，该检测器相比组合自适应归一化匹配滤波（CANMF）检测器具有更好的检测性能。

目标检测；长时累积；逆伽马纹理；海杂波；组合自适应广义似然比线性门限检测器。

1 引言

海杂波背景下的微弱运动目标检测问题一直以来都是一个热点问题［1-4］，这与它的应用前景是分不开。由于高分辨率海杂波序列中出现了一定数目的海尖峰分量（幅度巨大的异常样本），它的统计特性明显偏离高斯假设或者幅度分布出现显著的重拖尾现象，从而造成传统检测器（高斯背景下）对微弱目标的漏检现象，严重影响了检测器的性能［5］。为了改善这种情形，不仅需要确定海杂波的可靠的统计模型，而且需要根据海杂波的统计模型和目标信号的特性设计合适的检测器［6］。

对于雷达高分辨率或低擦地角条件下的海杂波的统计特性，文献［7］分析了不同条件下 IPIX（Ice multi-Parameter Imaging X）雷达获得的海杂波数据，并指出雷达距离分辨率或极化方式会影响海杂波的统计特性；文献［8］分析了不同波高和风向条件下几种常见的经典统计分布模型以及典型参数的Pareto分布对L波段小擦地角海杂波数据的拟合效果，为实际雷达目标检测中的海杂波建模提供参考依据。虽然不同条件下的海杂波数据的杂波幅度分布的具体形式也可能不同，但它们的幅度分布几乎都可以看作是来自复合高斯杂波模型。根据复合高斯杂波模型，杂波向量可以被建模为非负的纹理分量与复高斯分布的散斑分量的乘积。通常来讲，纹理分量在几个相干处理时间间隔内是可以被看作是一个常数［9］。因此，在这种纹理假设下，复合高斯杂波模型退化为球不变随机向量（Spherical Invariant Random Vector ， SIRV）模型。可以证明，现有的杂波幅度分布模型几乎都是 SIRV模型下的特例，文献［10］给出了几种常见杂波幅度分布与SIRV模型之间的对应关系以及基于 SIRV模型的不同分布的杂波的仿真方法。

当纹理服从Gamma分布时，杂波即为K分布杂波。在K杂波背景下，最优的检测器称为OKD（Optimum K-distributed Detector）［11］。虽然巨大的计算量代价限制了 OKD的广泛应用，但这不并影响对OKD的特性的研究，文献［12］指出：当海尖峰与正常杂波的相关特性相同时，海尖峰分量并不会引起OKD更多的虚警。当纹理服从逆伽马（Inverse Gamma， IG）分布时（纹理的倒数服从Gamma分布），对应的杂波强度的分布是广义的Pareto分布，而该杂波背景下最优的检测器称为 GLRT-LTD（Generalized Likely Ratio Test-Linear Threshold Detector）［13］。与OKD相比，GLRT-LTD的检测统计量具有简洁的表示式，这为它能够在实际检测问题中的应用创造条件。该文就以IG纹理的复合高斯分布（Compound Gaussian Distribution， CGD）对海杂波进行建模，提出一种适用于长时累积条件下的海杂波背景下的微弱运动目标的自适应检测方法。

关于 IG纹理的复合高斯杂波的研究工作如今已经有很多，如文献［13，14］验证了IG纹理的复合高斯模型对实测数据的有效性，同时分别给出了模型的形状参数和尺度参数的矩估计方法和最大似然估计方法；文献［15］给出了杂波的散斑协方差矩阵的最大似然估计方法；文献［16］推导了基于IG纹理的知识辅助检测器在先验模型参数失配条件下的虚警概率，Swerling-I型目标的检测概率的计算公式；文献［17］分析了基于归一化样本协方差矩阵的自适应GLRT-LTD的恒虚警特性。然而，在这些与目标检测有关问题中，更多考虑的是杂波的统计特性，而目标信号只是简单地被建模为导向矢量和未知复数的乘积模型。

实际上，目标信号也只有在数十个毫秒的时间内才可以被建模为乘积模型。然而，对于海面上的微弱动目标的检测问题，检测器通常需要累积足够多的脉冲以便抑制杂波，再加上目标的机动性以及受海浪和风速等因素的影响，长时累积时的目标信号的幅度调制和多普勒频率扩散不可避免，目标信号的能量会集中在某几个连续的多普勒通道中。此外，受海杂波空间非均匀性的影响，长时累积时所需要的参考单元数目往往小于脉冲累积数目。因此，在这种情形下是没有办法直接使用任何的传统自适应检测方法。为了可以利用长时累积带来的信号增益，同时很好地匹配杂波和目标的特性，该文提出组合自适应 GLRT-LTD的检测方法 CA-GLRTLTD。与文献［18］的方法类似，CA-GLRT-LTD的检测统计量由几个连续的短的时间间隔上的自适应GLRT-LTD的检测统计量的最大值的乘积构成。当目标信号的多普勒频率在这几个短的时间间隔上变化时，使用CA-GLRT-LTD可以判断待测单元中是否含有目标信号。

本文其余章节安排如下，第2节简要介绍IG纹理的复合高斯模型；在IG纹理的复合高斯杂波假设下，第3节提出一种适用于长时累积条件下的海杂波背景下的微弱动目标的CA-GLRLT-LTD的检测方法；第4节采用实测数据，通过与组合自适应归一化匹配滤波（ANMF）检测器作对比，验证所提出方法的有效性并在仿真数据条件下研究了所提检测器在K杂波背景下的性能损失；第5节总结全文。

2 杂波模型

实验表明，海杂波可以采用复合高斯模型进行很好的描述［7-9］。复合高斯杂波模型将海杂波看作两个独立分量（散斑分量和纹理分量）的乘积模型：

其中，τ称为纹理分量，它的取值与雷达入射角、场景大尺度变化有关，代表了雷达后向散射局部功率的大小；x称为散斑分量，它是N维零均值、协方差矩阵为R的复的圆高斯随机向量，它与雷达和场景间相对位置和相对运动有关，反映的是雷达接收机的相关特性。对于式（1）的CGD杂波，其概率密度函数为

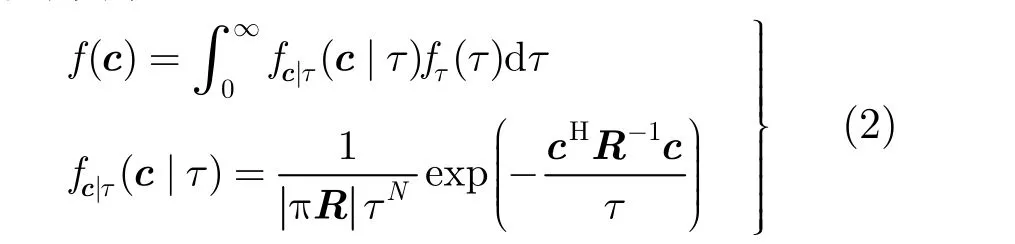
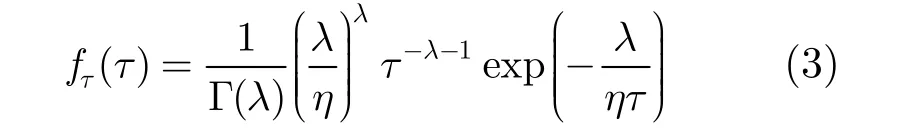
其中，λ，η分别表示纹理分布的形状参数和尺度参数。将式（3）代入式（2）得到杂波向量的概率密度函数为

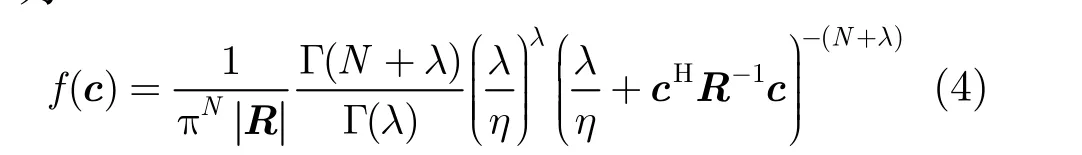
式（4）表示自由度为λ复的N元t分布，关于它的有效性，文献［12，13］均采用实测海杂波数据对此做过验证。由式（4）易知，IG纹理的CGD背景下的最优GLRT-LTD的匹配滤波形式为

其中， p0（fd）是多普勒导向矢量，z是接收到观测向量， fd表示目标的多普勒频率， Tr是雷达脉冲重复周期， T0是判决门限。

3 组合自适应GLRT-LTD（CA-GLRT-LTD）

在介绍组合自适应GLRT-LTD之前，首先对长时累积条件下的检测问题进行描述，与短时累积条件下的目标检测问题稍有不同，目标信号不再是简单的乘积模型。

3.1检测问题概述

设 z（ 1），z（ 2），…， z（N）是某一时间内接收到的时间序列，记 z≜［z（1），z（ 2），…，z（N ）］T=zI+j zQ，其中， zI和 zQ分别表示向量z的同相分量和正交分量。对于目标检测问题，向量z对应两种可能情形：（1）它仅由杂波组成；（2）它由杂波和信号的加和组成，即下面的二元假设检验问题：

其中，z，s和c分别代表待测单元中的接收向量、感兴趣的目标信号和服从式（4）概率分布的杂波向量；zk或 ck是待测单元周围的K个参考单元中的杂波向量。对于海面上的微弱动目标检测问题，为了更好地抑制杂波对目标的影响，检测器需要累积足够多的脉冲数目 N。然而，受限于海杂波空间非均匀性，长时累积条件下自适应检测器可用的参考单元数目K往往是小于N。除此以外，相干处理中的目标信号的点目标模型仅限于脉冲累积数目不太多的情形。当脉冲累积数目较多时，目标信号是不可以简单地表示为导向矢量和未知复数的乘积模型，但它的每个分量仍然可以表示为

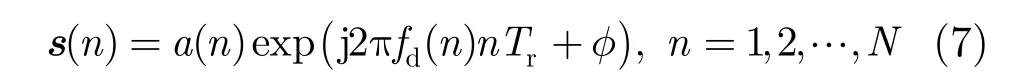
其中， a（n）和 fd（n）分别称为信号 s（ n）的幅度调制和瞬时多普勒频率； Tr是雷达脉冲重复周期，φ是信号 s（ n）的初始相位。当检测器作长时累积时，信号的幅度调制 a（n）和瞬时多普勒频率 fd（n）都将是时间n的慢变函数。因此，由于长时累积条件下目标信号的幅度和瞬时多普勒频率的变化以及海杂波的空间非均匀性对参考单元数目的限制，传统的自适应检测器是不能直接解决式（6）中的检测问题。然而，由幅度和瞬时多普勒频率的慢变特性可知，长时累积条件下目标信号的幅度和瞬时多普勒频率都可以采用分段的常函数进行逼近。基于这一思想，并结合杂波的统计特性，该文提出一种称为组合自适应GLRT-LTD的检测方法。

3.2 组合自适应GLRT-LTD

与文献［18］作法相似，组合自适应 GLRT-LTD将式（6）中的向量分割为一系列长度为M的短向量。不失一般性，假定M满足关系式N=QM，其中，Q是某一正整数。那么式（6）中的向量可以表示为

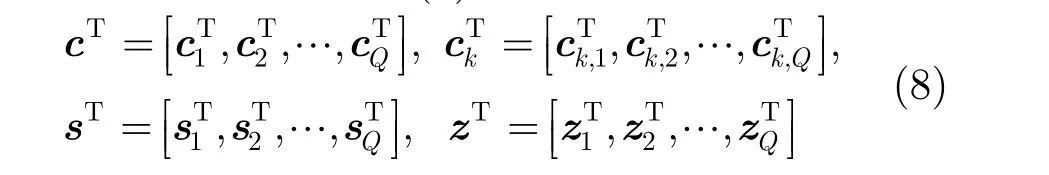
经均匀分割后，原本长度为NTr的累积时间被等分Q个长度为MTr的子时间间隔。在每个子时间间隔中，短的杂波向量可以采用 SIRV进行建模，而目标信号可以采用导向矢量和未知复数的乘积模型进行近似。因此，在每个子时间间隔中，可以计算GLRT-LTD的检测统计量在每个多普勒频率 fd上的取值为

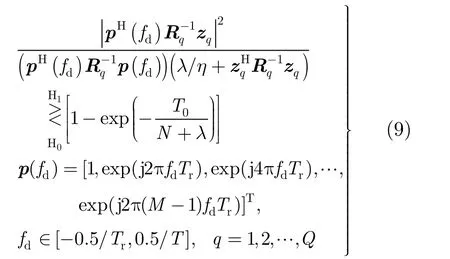
其中， p（ fd）是长度为M的多普勒导向矢量，λ和η是纹理分布的形状参数和尺度参数，Rq是第q个子时间间隔上杂波的散斑协方差矩阵，这里假定λ，η和 Rq是已知量。应用中，可以使用参考单元中杂波数据对它们进行估计，从而得到自适应 GLRTLTD。对于参数λ和η，可以采用矩估计方法［13］或最大似然估计方法［14］。散斑协方差矩阵 Rq采用文献［15］中的最大似然（Maximum Likelihood， ML）估计方法，其估计值由参考单元中的杂波向量采用迭代的方法得到。

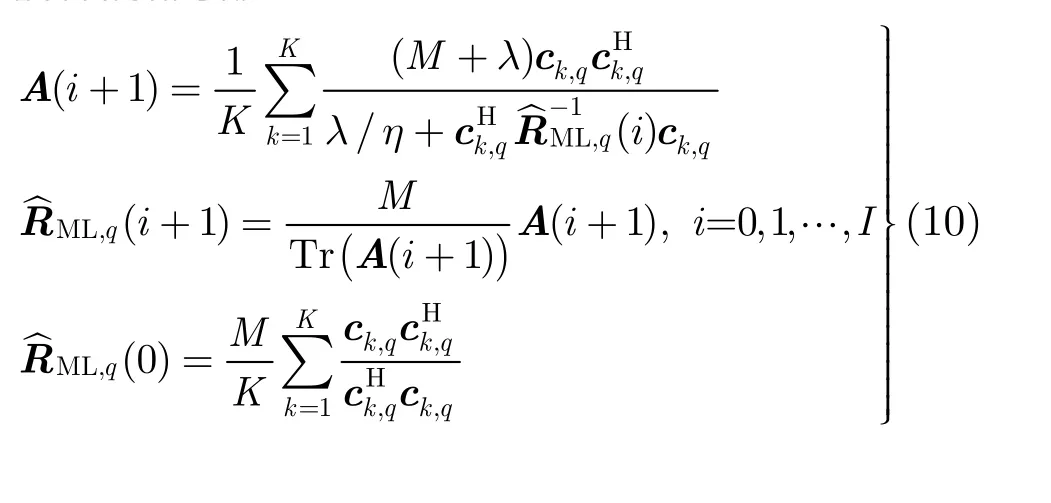
其中，符号Tr（*）表示的矩阵*的迹，参数I代表迭代次数，这里取 I= 5，因为更多次数的迭代所能带来的检测器的性能改善是不明显的。由于向量经过均匀分割处理后得到短的子向量的长度M=N/Q小于参考单元数目 K，因此，各个子时间间隔上的参考单元可以很好地估计所在时间间隔上的散斑协方差矩阵。将散斑协方差矩阵的估计值R︿ML，q代入式（9），得到自适应的GLRT-LTD（式（11）中参数λ和η表示它们的估计值）：

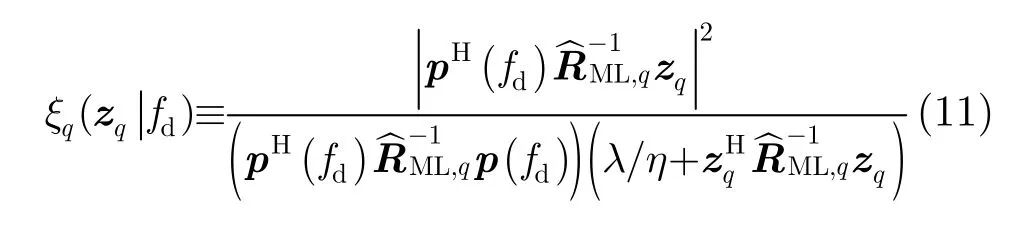
在长的累积时间前提下，每个子时间间隔中的信号能量集中在某一多普勒通道，而且各个时间间隔中的信号能量所处的多普勒通道是不同的。鉴于此，定义一个新的检测统计量，它是自适应GLRTLTD在所有时间间隔上响应的最大值的乘积，即组合自适应GLRT-LTD，以此实现对信号能量的进一步累积。

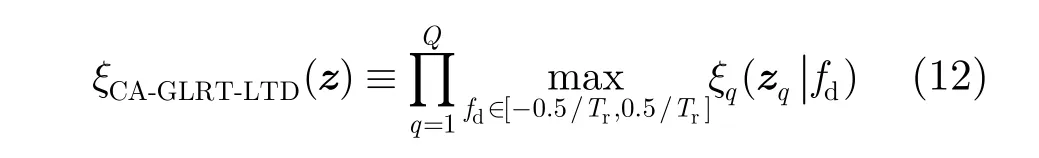
由式（12）可知，计算检测统计量的运算量是非常大的，因为 fd的取值选自闭区间 ［-0.5/ Tr， 0.5/ Tr］。为了降低运算量同时减少因多普勒频率失配引起的检测器的性能损失，在频率域采用过4采样处理，即多普勒频率的取值依次为 fd=0，±1 /（4 MTr），±2/（4 MTr），…，±2M/（4M Tr）。当参数N和M给定时，使用Monte-Carlo实验方法便可以计算给定虚警概率条件下的判决门限。

理论上，当短向量长度M满足信号真实模型与假定模型之间的误差最小时，最小的累积长度N应该满足使得信号累积增益足够大于杂波的增益。由于杂波的统计特性受海态，雷达分辨率、工作频率、极化方式等方面因素的影响［5，7］，最小的累积长度N的选择是依赖于数据。然而，在数据量充足条件下，当短向量长度M选择合适时，向量长度N越大，组合检测器对应的检测性能越好。

4 实验部分

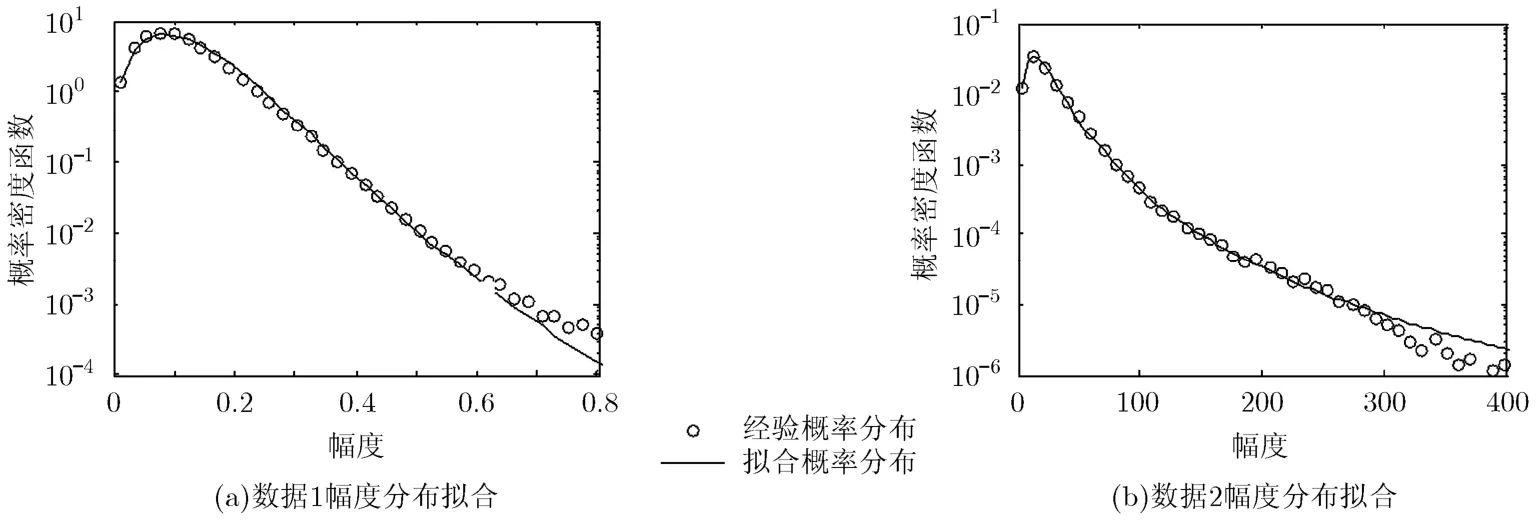
图1 实验数据的经验概率密度函数和理论概率密度函数

本节采用两种实测海杂波数据进行实验，其中数据1（TFA10_006.mat）由X波段的Fynmeet雷达［19］采用VV极化采集得到，数据由64个距离单元，164919个相干脉冲序列组成，距离分辨率为15 m，雷达脉冲重复频率fr=2.5 kHz；数据2（19980212_ 195704_ANTSTEP.mat）由IPIX雷达［20］采集得到，数据由28个距离单元，60000个相干脉冲序列组成，距离分辨率为30 m，脉冲重复频率fr=1.0 kHz，为保持一致性，这里使用VV极化方式获得数据进行实验。数据1中的测试目标为一艘小船，在整个观测时间内，雷达采用跟踪模式对小船进行监测，并将带有小船的反射信息的数据始终存储在第 16个距离单元；数据2中的测试目标为一被固定在海面上的直径为1 m的漂浮的金属球，雷达采用驻留模式对小球进行监测，有关小球的反射信息的数据存储在第7个距离单元。为了降低数据的脉冲重复频率，同时在谱不出现混叠的前提下，分别对数据 1和数据 2进行下 4和下 2采样处理，然后采用逆Gamma纹理的CGD对处理后的海杂波数据进行建模。图1分别画出了数据1删除第14～18个距离单元后和数据2删除第6～8个距离单元后的海杂波数据的经验幅度概率密度函数曲线和采用式（3）的纹理分布的理论概率密度函数曲线，其中，杂波幅度分布的形状参数λ和尺度参数η采用经典的矩估计方法得到（（a）λ=5.2158，η=62.9767；（b）λ=1.4336，η=0.0024）。由图1可知，逆Gamma纹理的CGD能够很好地表征实验数据的幅度分布，这为能够使用自适应GLRT-LTD提供依据。图2画出了目标所在距离单元数据对应的谱图，图中的蛇形曲线代表了目标信号的瞬时频率曲线。由图2可知，目标信号的多普勒频率具有明显的扩散现象，这与前面对目标信号的瞬时频率特性的假设是一致的，此外，图2（b）的瞬时频率的变化速率要明显高于图2（a）的瞬时频率，这意味着在实验中数据2所选的子时间间隔要短于数据1的子时间间隔。

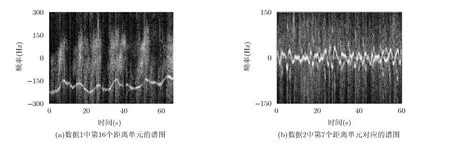
图2 实验所用数据的目标距离单元数据对应的谱图

实验中，虚警概率PFA设为 1 × 10-3，考虑到数据1和数据2所能使用的纯杂波数据量的大小的不同以及瞬时频率的变化速率不同，对于数据 1，累积的脉冲数目 N= 512，每个子时间间隔中的累积脉冲数目 M= 16，相应的子时间间隔的数目Q= N/M=32；对于数据2，对应的参数依次为N=256，M=8， Q=N/M=32。由于海杂波空间的非均匀性，数据1中的参考单元只取待测单元周围邻近的32个距离单元，而数据2中的参考单元由除了目标单元和两个影响单元之外的其余单元组成。当 N=512，M=16时，数据1的每个距离单元的时间序列被均匀地分割为80个不相交的长度为512的待测向量，并将每一个待测向量记为一个时间距离单元。因此，数据1中所有时间距离单元的个数为80×64=5120。同理可知，数据 2中所有时间距离单元的个数为117×25=2925。按照式（12）计算每个时间距离单元对应的组合自适应GLRT-LTD检测统计量的取值，并由此确定组合自适应 GLRT-LTD的检测门限和检测概率。为了说明组合自适应GLRT-LTD的检测结果的优势，图3和图4同时也画出了组合自适应归一化匹配滤波（ANMF）检测器对实验数据的检测结果。图3中的第16距离单元以外的5个时间距离单元和图4中的第7距离单元以外的3个时间距离单元表示两种组合自适应检测器的虚警点。其中，图3中的组合自适应GLRT-LTD相比组合ANMF检测器在性能改善了7.5%，检测概率分别为83.75%和76.25%，图4中的组合自适应GLRT-LTD相比组合ANMF检测器在性能改善了5.13%，检测概率分别为82.91%和77.78%。对于其他数据，只要IG纹理的 CGD能够很好地表征杂波的统计特性，组合自适应GLRT-LTD相比组合ANMF检测器都有不同程度的改善。限于篇幅，这里没有给出其他数据的检测结果。然而，组合自适应GLRT-LTD相比组合ANMF检测器的性能改善程度是不可能很多，这是因为在杂波重拖尾或者脉冲累积数目比较多时，ANMF检测器具有渐近最优检测性能的特性。

实际应用中，杂波服从哪种分布是事先不清楚的，因此，组合自适应GLRT-LTD可能面临杂波模型失配的情形。考虑到K杂波对实测数据的良好拟合效果，下面以仿真K杂波为例，分析了组合检测器在K杂波中的检测性能。其中，K分布的表示式为

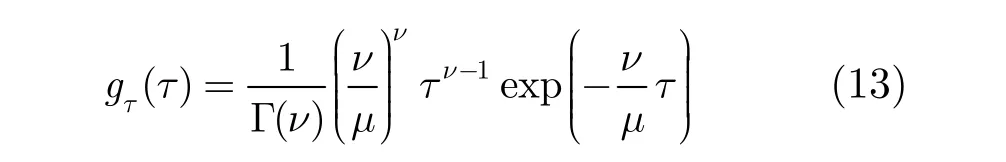
仿真的目标信号根据数据2中的真实目标信号的特性产生。

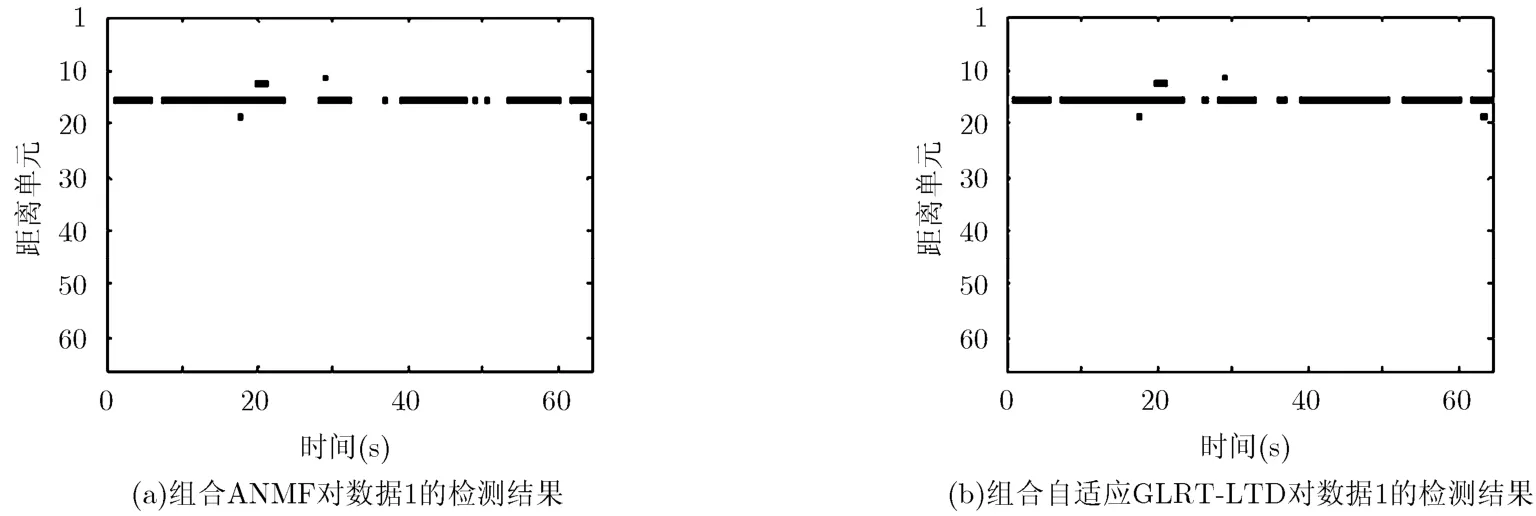
图3 当N=512， M=16， K=32和 PFA=1.0 × 10-3时，两种组合自适应检测器分别对数据1的检测结果（（a）76.25%； （b）83.75%）

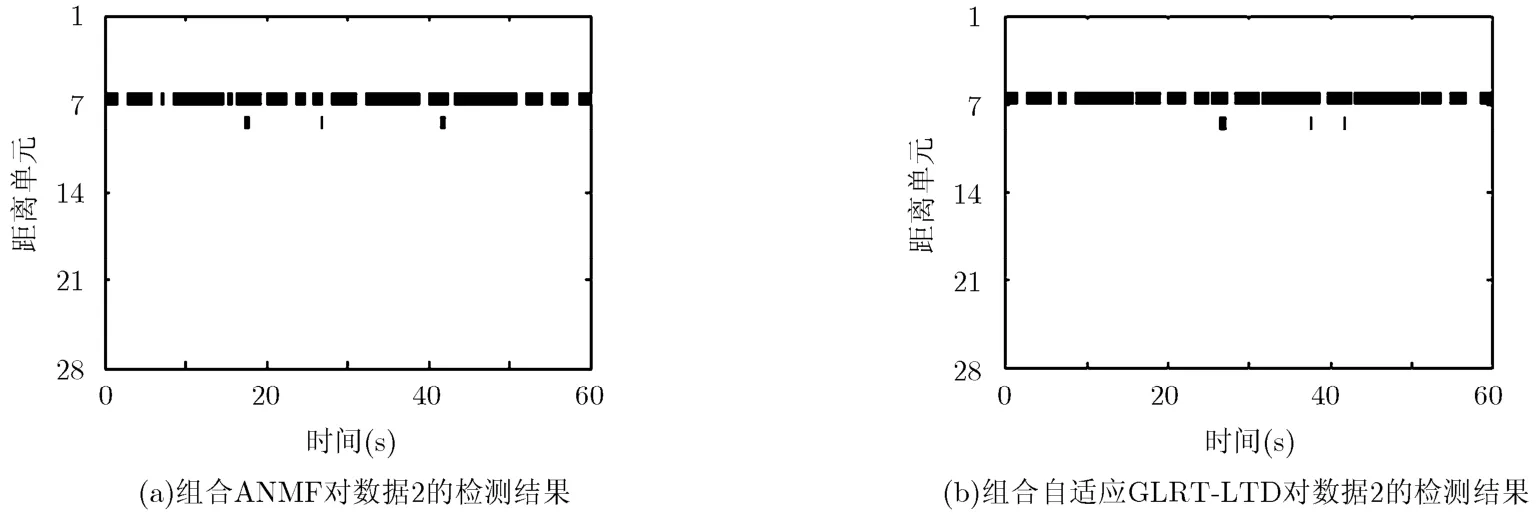
图4 当N=256， M=8， K=25和 PFA=1.0 × 10-3时，两种组合检测器对数据2的检测结果（（a）77.78%； （b）82.91%）

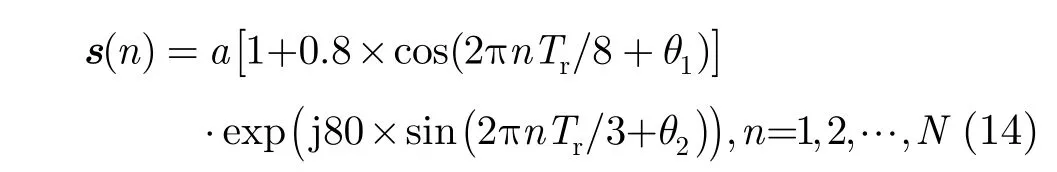
其中，随机常数a用来调节信号的信杂比，起伏项用来描述目标横截面积随机时间的变化，指数项用来描述目标的多普勒频率随时间的变化，参数 θ1和 θ2是服从均匀分布。当采用矩匹配方法（一阶矩的平方与二阶矩的比值相等）时，可以得到IG分布的形状参数λ与K分布的形状参数v的关系式为λ = v+1，而尺度参数（η， μ）选择使得杂波满足单位功率。对于满足式（14）形式的目标和杂波为K杂波的目标检测问题，可以设计组合的自适应 OKD检测器。

从图5可知：当 v =0.5，组合自适应GLRT-LTD相比组合自适应OKD具有1 dB的性能损失，当v大于1时，组合自适应GLRT-LTD具有与组合自适应 OKD相当的检测性能。这是因为小形状参数条件下K杂波与IG杂波的模型失配程度更高，这一点可以使用两种分布的形状参数的相对误差（（λ - v ）/v）给予说明。

5 结束语

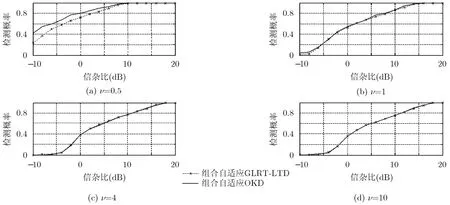
图5 当N=256， M=8， K=25和 PFA=1.0 × 10-3时，组合自适应检测器在仿真K杂波中的检测性能

通过分析海杂波的统计特性和目标信号的瞬时频率曲线，本文提出了组合自适应GLLRT-LTD的检测方法。该方法利用长时累积条件下目标信号的幅度和瞬时频率的慢变特性，成功地克服了海杂波背景下的传统自适应检测器的长的累积时间与短的均匀距离间隔之间的矛盾。由于自适应 GLLRTLTD对于各个子时间间隔上的逆Gamma纹理复合高斯杂波的最优特性，使得它的检测性能优于组合ANMF检测器。此外，在形状参数大于1的仿真K杂波背景下，组合自适应GLLRT-LTD具有十分稳健的检测性能。

［1］ Moya J C， Menoyo J G， Lopez A A， et al.. Small target detection in high-resolution heterogeneous sea-clutter: an empirical analysis［J］. IEEE Transactions on Aerospace and Electronic Systems， 2011， 47（3）: 1880-1898.

［2］ Chen Xiao-long， Cai Yong， and Cai Fu-qing. Application of the sparse decomposition to micro-motion target detection embedded in sea clutter［C］. Proceedings of the 2013 International Conference on Radar， Adelaide， Canada， 2013: 163-166.

［3］ Chen Si-jia， Kong Ling-jiang， and Yang Jian-yu. Adaptive detection in compound-Gaussian clutter with partially correlated texture［C］. Proceedings of the 2013 IEEE Radar Conference， Ottawa， Canada， 2013: 1-5.

［4］ Chen Xiao-long， Guan Jian， He You， et al.. Detection and extraction of target with micro-motion in spiky sea clutter via short-time fractional Fourier transform［J］. IEEE Transactions on Geoscience and Remote Sensing， 2014， 52（2）: 1002-1018.

［5］ Ward K D， Tough R J A， and Watts S. Sea Clutter: Scattering， the K Distribution and Radar Performance［M］. London， United Kingdom: The Institution of Engineering and Technology， 2006: 230-266.

［6］ Sangston K J and Gerlach K R. Coherent detection of radar targets in a non-Gaussian background［J］. IEEE Transactions on Aerospace and Electronic Systems， 1992， 28（1）: 208-216.

［7］ Greco M V， Gini F， and Rangaswamy M. Statistical analysis of measured polarimetric clutter data at different resolutions［J］. IEE Proceedings-Radar， Sonar and Navigation， 2006，153（6）: 473-481.

［8］ 张玉石， 许心瑜， 尹雅磊， 等. L波段小擦地角海杂波幅度统计特性研究［J］. 电子与信息学报， 2014， 36（5）: 1044-1048. Zhang Yu-shi， Xu Xin-yu， Yin Ya-lei， et al.. Research on amplitude statistics of L-band low grazing angle sea clutter［J］. Journal of Electronics & Information Technology， 2014，36（5）: 1044-1048.

［9］ Moya J C， Menoyo J G， Lopez A A， et al.. Statistical analysis of a high-resolution sea-clutter database［J］. IEEE Transactions on Geoscience and Remote Sensing， 2010， 48（4）: 2024-2037.

［10］ Rangaswamy M， Weiner D， and Ozturk A. Computer generation of correlated non-Gaussian radar clutter［J］. IEEE Transactions on Aerospace and Electronic Systems， 1995，31（1）: 106-116.

［11］ Gini F， Greco M V， Farina A， et al.. Optimum and mismatched detection against K-distributed plus Gaussian clutter［J］. IEEE Transactions on Aerospace and Electronic Systems， 1998， 34（3）: 860-876.

［12］ Yang D. Optimal coherent radar detection in a K-distributed clutter environment［J］. IEE Proceedings-Radar， Sonar and Navigation， 2012， 6（5）: 283-292.

［13］ Sangston K J， Gini F， and Greco M V. Coherent radar target detection in heavy-tailed compound-Gaussian clutter［J］. IEEE Transactions on Aerospace and Electronic Systems，2012， 48（1）: 64-77.

［14］ Balleri A， Nehorai A， and Wang J. Maximum likelihood estimation for compound-Gaussian clutter with inverse gamma texture［J］. IEEE Transactions on Aerospace and Electronic Systems， 2007， 43（2）: 775-780.

［15］ Greco M V and Gini F. Cramer-Rao lower bounds for covariance matrix estimation of complex elliptically symmetric distributions［J］. IEEE Transactions on Signal Processing， 2013， 61（24）: 6401-6409.

［16］ 邹鲲， 廖桂生， 李军， 等. 非高斯杂波下知识辅助检测器敏感性分析［J］. 电子与信息学报， 2014， 36（1）: 181-186. Zou Kun， Liao Gui-sheng， Li Jun， et al.. Sensitivity analysis of knowledge aided detector in non-Gaussian clutter［J］. Journal of Electronics & Information Technology， 2014， 36（1）: 181-186.

［17］ Zhao Yi-nan， Pang Xiao-yu， and Yin Bin. Adaptive radar detection for targets in compound-Gaussian clutter with inverse gamma texture［C］. Proceedings of the IET International Radar Conference， Xi’an， China， 2013: 1-4.

［18］ Shui Peng-lang， Li Dong-chen， and Xu Shu-wen. Tri-featurebased detection of floating targets in sea clutter［J］. IEEE Transactions on Aerospace and Electronic Systems， 2014，50（2）: 1416-1430.

［19］ The Defence， Peace， Safety， and Security Unit of the Council for Scientific and Industrial Research. The Fynmeet radar database［OL］. http://www.csir.co.ca/small_boat_detection，2014.2.10.

［20］ Cognitive System Laboratory， McMaster University， Canada. The IPIX radar database［OL］. http://soma.mcmaster.ca// ipix.php， 2012.10.11.

刘 明： 男，1986年生，博士生，研究方向为海面微弱动目标检测.

水鹏朗： 男，1967年生，博士，教授，研究方向为多速率滤波器理论及应用、图像处理和雷达目标检测.

Combined Adaptive GLRT-LTD against Sea Clutter

Liu Ming Shui Peng-lang
（National Key Laboratory of Radar Signal Processing， Xidian University， Xi’an 710071， China）

Long integration is often required to detect weak moving target in sea clutter. However， the Doppler frequency spread and amplitude fluctuation in long integration and limited reference cells resulting from spatial non-homogeneity of sea clutter make the traditional adaptive detector work badly. By observing that the Compound Gaussian Distribution （CGD） with Inverse Gamma （IG） texture gives a good fit to sea clutter and the instantaneous frequency is slowly varying， a combined adaptive detector， namely the Combined Adaptive Generalized Likelihood Ratio Test-Linear Threshold Detector （CA-GLRT-LTD）， is proposed in the paper， which consists of the product of the maximal response of the adaptive GLRT-LTD in several continuous short integration intervals. Owing to the optimality of the GLRT-LTD for CG clutter with IG texture， the proposed detector obtains better performance than the Combined Adaptive Normalized Matched Filter （CANMF） detector.

Target detection； Long integration； Inverse Gamma （IG） texture； Sea clutter； Combined Adaptive Generalized Likelihood Ratio Test-Linear Threshold Detector （CA-GLRT-LTD）

The National Natural Science Foundation of China （61271295）

TN959.72

A

1009-5896（2015）12-2984-07

10.11999/JEIT150588

2015-05-18；改回日期：2015-09-02；网络出版：2015-11-01

*通信作者：刘明 mingliu1608@163.com

国家自然科学基金（61271295）