MD-64算法的相关密钥-矩形攻击

郭建胜崔竞一罗 伟刘翼鹏（信息保障技术重点实验室 北京 100072）（解放军信息工程大学 郑州 450001）（解放军78179部队 成都 611830）

MD-64算法的相关密钥-矩形攻击

郭建胜*①②崔竞一②罗 伟③刘翼鹏②
①（信息保障技术重点实验室 北京 100072）②（解放军信息工程大学 郑州 450001）③（解放军78179部队 成都 611830）

该文针对 MD-64分组密码算法在相关密钥-矩形攻击下的安全性进行了研究。分析了算法中高次 DDO（Data Dependent Operations）结构、SPN结构在输入差分重量为1时的差分转移规律，利用高次DDO结构的差分特性和SPN结构重量为1的差分路径构造了算法的两条相关密钥-差分路径，通过连接两条路径构造了算法的完全轮的相关密钥-矩形区分器，并对算法进行了相关密钥-矩形攻击，恢复出了32 bit密钥。攻击算法所需的数据复杂度为262相关密钥-选择明文，计算复杂度为291.6次MD-64算法加密，存储复杂度为266.6Byte存储空间，成功率约为0.961。分析结果表明，MD-64算法在相关密钥-矩形攻击条件下的安全性无法达到设计目标。

分组密码；密码分析；MD-64算法；相关密钥-矩形攻击

1 引言

近年来，基于相关密钥的复合攻击成为分组密码分析领域的研究热点，其中相关密钥-差分攻击方法极大促进了密码分析的发展［1-4］。矩形攻击是一种常见的差分分析手段，文献［5］利用飞来去器攻击给出了LBlock算法的分析结果；文献［6］利用相关密钥-矩形攻击对KASUMI算法进行了攻击实验；文献［7］利用相关密钥-飞来去器攻击给出了KATAN32 /48/64算法的分析结果，文献［8］利用相关密钥-飞来去器攻击给出了MMB算法的分析结果。

在分组密码设计当中，DDP（Data-Dependent Permutation）［9］， DDO（Data-Dependent Operations）［10］，高次DDO［11］等比特控选结构具有可并行计算、执行效率高、易于软硬件实现、数据处理规模灵活、应用范围广泛等优点，被广泛应用于分组密码算法设计［12-14］。目前，针对应用上述结构的分组算法的安全性分析成果较少，分析这类算法的安全性具有十分重要的意义。

作为高次DDO结构的一个典型应用，MD-64算法由文献［11］于2010年提出。算法设计者利用高次DDO结构提升了算法的执行效率和资源利用率。与此同时，设计者在算法圈函数一路数据处理过程中引入了SPN结构，实现了对数据的扩散和置乱。安全性分析方面，设计者构造了一条概率约为的两轮循环差分链，并认为8轮迭代使得MD-64算法能够抵抗所有差分类型攻击。文献［15］于2011年对MD-64算法进行了相关密钥-扩大飞来去器攻击，文献［16］对MD-64算法同样进行了相关密钥-扩大飞来去器攻击，但二者均未分析攻击算法的存储复杂度和成功率。

本文研究了MD-64算法在相关密钥-矩形攻击下安全性，利用高次DDO结构和SPN结构存在的信息泄漏规律构造了算法的两条高概率相关密钥-差分路径，进而给出了算法的全轮相关密钥-矩形区分器，在相关密钥-选择明文条件下对算法的进行了攻击，攻击算法所需的数据复杂度为 262个相关密钥-选择明文，计算复杂度为 291.6次 MD-64算法加密，存储复杂度为266.6Byte存储空间，成功率约为0.961。

2 相关知识

2.1 符号说明

下面对本文所使用的符号进行说明，K表示算法主密钥，P表示算法的明文输入，C表示算法的密文输出。第i轮的轮函数左半分组与右半分组分别记为 Li与 Ri， ΔLi与 ΔRi分别表示第i轮的轮函数左半分组的输入差分与右半分组的输入差分。 ΔQi与为第i圈加密圈子密钥的差分与解密圈子密钥的差分。ei表示第i位非零且其余位为零的32 bit数据块， ei，j第i位与第j位非零且其余位为零的32 bit数据块。

2.2 MD-64算法

MD-64算法分组规模为64 bit，密钥规模为128 bit，迭代轮数为8轮。算法圈函数将64 bit输入数据分成两路32 bit数据块，其中一路数据主要利用高次DDO结构进行处理，另一路数据利用SPN结构进行处理，能够同时对两路数据进行扩散和置乱。算法整体结构和圈函数结构分别如图1（a）和图1（b）所示，圈函数中SPN结构如图2所示。

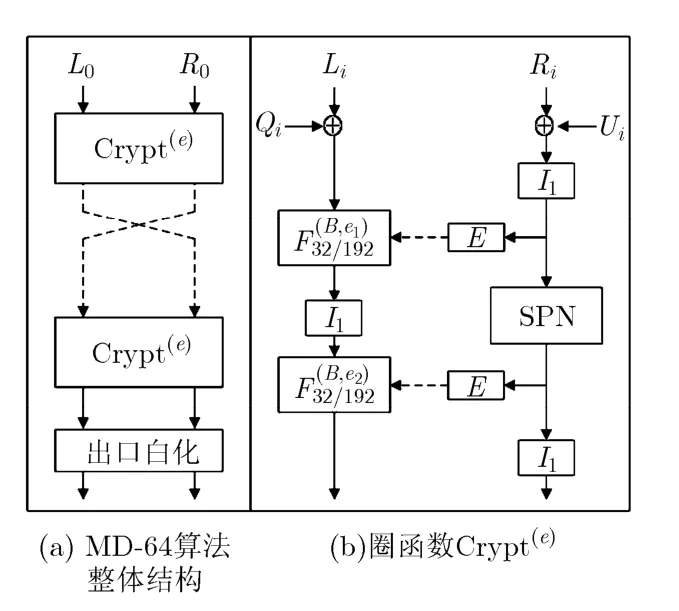
图1 MD-64算法示意图

图2 SPN结构示意图

线性变换 P1：

线性变换 P2：

线性变换 P3：

（1，3，19，17）（2，7，20，21）（4，23，18，5）（6，8，24，22）

（11，27，25，9）（10，15，28，29）（12，31，26，13）（14，16，32，30）

表1 大小为4×4的S盒

表2 MD-64算法圈子密钥

线性变换 I1：

记拓展变换E的32 bit输入为 （B1，B2）， 192 bit输出为Z6），则

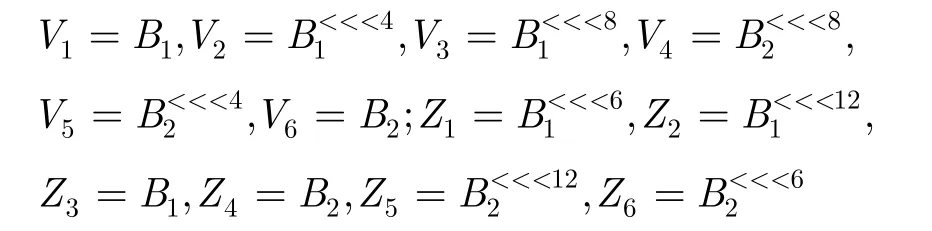
其中 B，V，Z均为16 bit数据， X＜＜＜n表示对16 bit

iii数据进行循环左移nbit。

2.3 相关密钥-矩形攻击算法

矩形攻击是一种差分类型的分析方法，于2005年由Biham等人［17］提出。矩形攻击的主要思想是通过连接两条短的高概率差分路径构造轮数更长区分器。假设算法E可以用表示， E0存在概率为p的差分路径α → β， E1存在概率为q的差分路径δ→ γ，若满足 （pq ）2＞ 2-n，则认为可以构造区分器将密码算法与随机置换区分开，其中n为算法分组规模。

相关密钥-矩形攻击是在矩形攻击中引入相关密钥，其目的是提升算法的攻击轮数，图3给出了相关密钥-矩形区分器示意图。

如图3所示，攻击者获得了密钥 K，K *，K'，K '*间的差分关系，但并不知道密钥的取值，在相关密钥条件下，利用两条短的高概率相关密钥-差分路径即可构造出轮数更长的相关密钥-矩形攻击区分器。

定义 1［17］若明文四元组（P，P'，P *，P'*）同时满足图3中所示的4条差分路径，则称其为正确四元组。

3 MD-64算法圈函数差分特性分析

3.1 基本单元差分特性分析

性质1当控制信息差分为0，基本单元 F2/2输入差分重量为1时，

证明当控制信息差分为0，基本单元 F2/2输入差分 Δx1Δ x2重量为1时，x1x2的取值情况只有同种01， 10。分别代入 y1与 y2的表达式中可得：

当输入 Δx1Δ x2为10时，通过控制vz取值遍历00， 01， 10， 11共4种情况，对应 y1y2的4个输出分别为10， 01， 10， 11。

当输入 Δx1Δ x2为01时，通过控制vz取值遍历00， 01， 10， 11共4种情况，对应 y1y2的4个输出分别为11， 10， 11， 01。 证毕

类似地，得到性质2和性质3。

性质2当控制信息差分为0，基本单元 F2/2输入差分重量为2时，

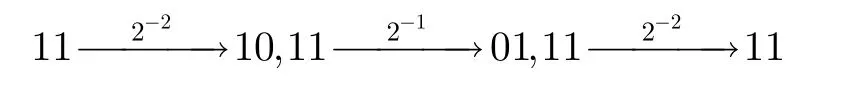
性质 3当基本单元 F2/2控制信息差分 Δv Δz重量为1时，

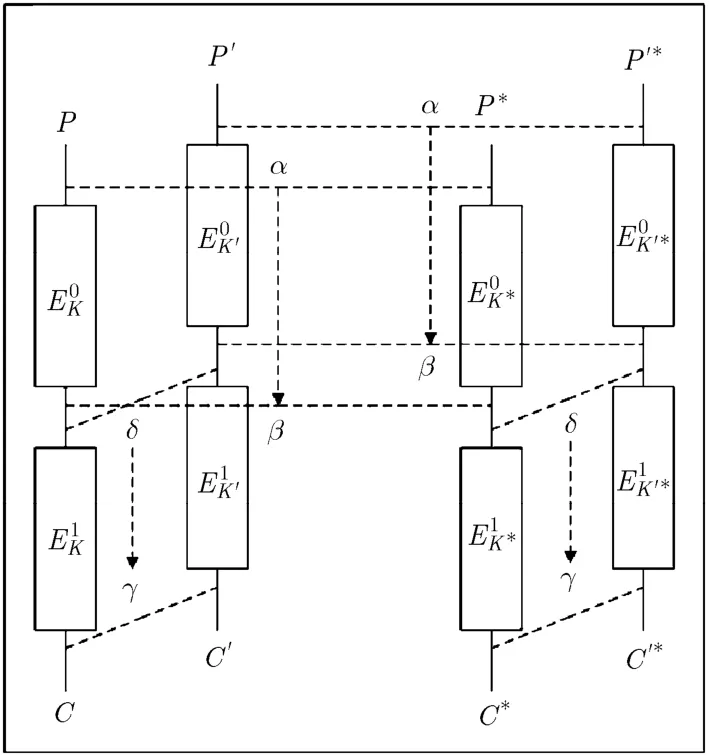
图3 相关密钥-矩形区分器示意图

3.2 SPN结构差分特性分析

通过实验模拟，遍历搜索得到SPN结构重量为1的最优差分路径，由表3给出。如表3所示，SPN结构重量为 1的最优差分路径为对于MD-64算法圈函数，由 I1知，圈函数输入差分为 （0，e13），密钥差分为（0，0）时，SPN结构输入差分为 e6，即圈函数右半部分存在输入输出重量为 1 的差分路径

4 MD-64算法圈的相关密钥矩形攻击

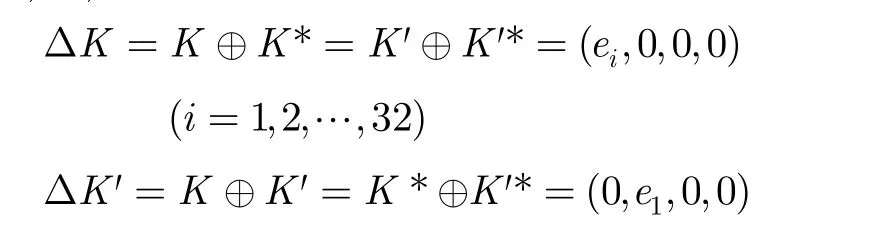
如表4所示，第1条相关密钥-差分路径长度为3轮（第1轮到第3轮），输入输出差分分别为α=密钥差分为差分转移概率为 p= 1；第2条相关密钥-差分路径长度为5轮（第4轮到第8轮），输入输出差分分别为密钥差分为 Δ K'= K ⊕ K' = K * ⊕K '* = （0，e1，0，0），其中k∈｛1，2，3，4，5｝， ？表示任意32 bit二元序列。

第2条相关密钥-差分路径中，第7轮输入差分为（0，0），密钥差分为 （e1，0），下面分析计算其输出差分为 （e1，13，0）的概率q'。

第7轮输入差分为（0，0），密钥差分为 （e1，0）时，函数的输入差分为 e1。利用性质1，图4加粗线条给出了使得函数G的输出差分为 e1，13的差分路径。

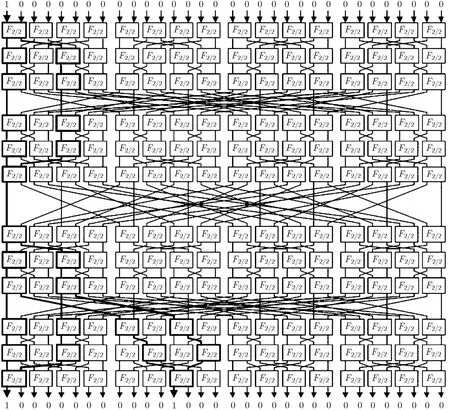
图4 F3 2/192 ·I1 ·F 32/192中 e1 → e1，13的一条差分路径

由于函数G输出差分重量2，因此1 bit输入差分在传递过程中必然会在经过某个基本单元 F2/2后，变换为2 bit差分，并最终传递到函数G输出的第1和第13个比特位。根据函数G的拓扑结构与假设，1 bit差分变换为2 bit差分的 F2/2所在基本单元层只能在第 2个 F32/192中，图4所示的差分路径中的差分路径的概率分为两个部分，其中

表3 SPN结构重量为1的最优差分路径

第2条相关密钥差分路径中，MD-64算法第7轮、第8轮的差分传递情况如图5所示。

相关密钥-矩形攻击算法步骤如表5所示。

根据上述相关密钥-差分路径，相关密钥-矩形攻击算法的成功率和复杂度分析分别由定理1和定理2给出。

定理1取 n= 61时，相关密钥-矩形攻击算法的成功率约为0.961。

证明取 n= 61时，相关密钥-矩形攻击算法步骤 1构造出个四元组。随机密文对差分为 （Δ CL，eI1（k））的概率为因此通过步骤 2 的密文四元组数量约为 2121×（2-29.7）2= 261.6个。

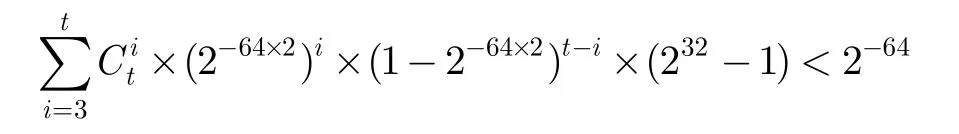
步骤3中，正确 K3的计数次数不小3次的概率为

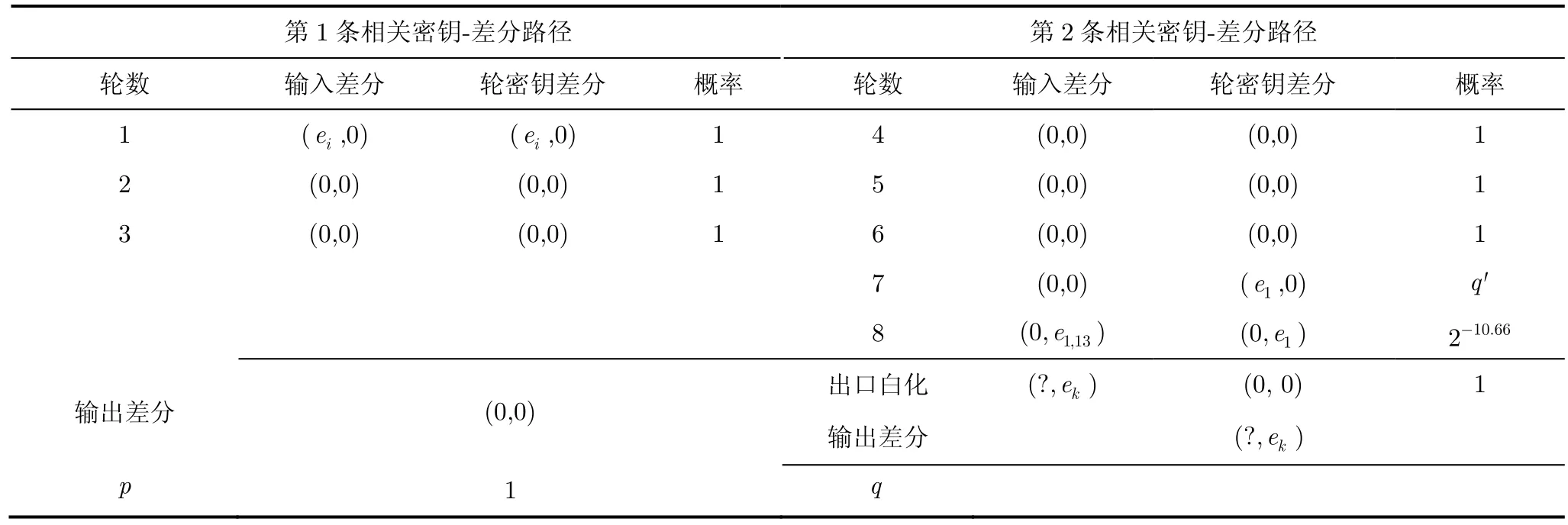
表4 MD-64算法的两条相关密钥-差分路径（k=1，2，3，4，5）

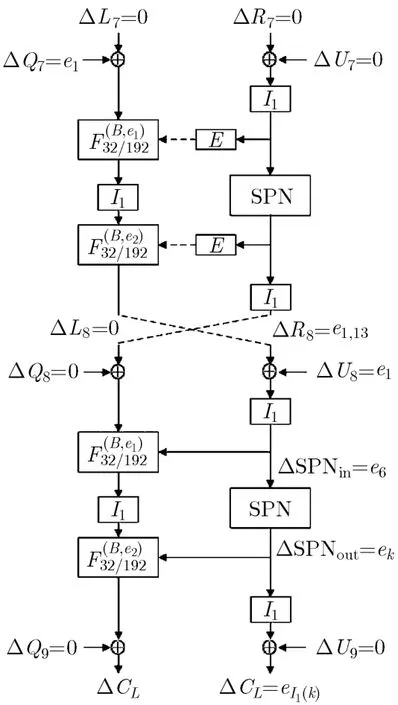
图5 MD-64算法最后两轮的差分传递情况

表5 相关密钥-矩形攻击算法

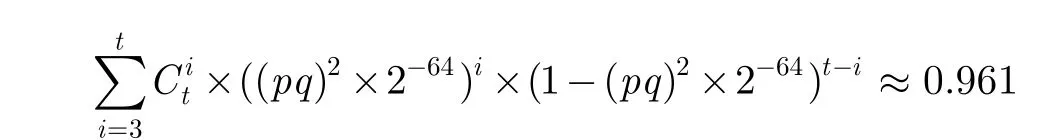
因此，攻击算法的成功率约为0.961。 证毕

定理2利用相关密钥-矩形攻击算法能够恢复出MD-64算法的128 bit密钥，相应的数据复杂度为 262个相关密钥-选择明文，计算复杂度为 291.6次MD-64算法加密，存储复杂度为 266.6Byte存储空间。

证明步骤1加密明文需要 2 × 2n= 262次MD-64算法加密。步骤 2存储密文四元组需要 261.6×4 ×8 = 266.6Byte存储空间。步骤3中反解一轮算法约为1/16次MD-64算法加密，因此步骤3所需的计算复杂度为 261.6× 232× 4 × 1/16 = 291.6次 MD-64算法加密。综上所述，利用相关密钥-矩形攻击算法恢复 32 bit密钥所需的数据复杂度为 262个相关密钥-选择明文，计算复杂度为 262+291.6≈ 291.6次MD -64算法加密，存储密钥度约为 266.6Byte存储空间。

证毕

表6给出了针对MD-64算法攻击结果的对比情况。

如表6所示，本文给出了针对MD-64算法完整分析结果，攻击算法整体复杂度为≈ 291.6，优于已有攻击结果的整体复杂度 295。

5 结束语

本文对MD-64算法进行了相关密钥-矩形分析，利用相关密钥构造了算法的高概率相关密钥-矩形区分器，并恢复出了32 bit算法主密钥。本文的分析结果表明，MD-64算法选用的SPN结构的数据规模相对较小，因此存在着明显的差分不平衡，从而造成部分信息泄漏；同时，攻击者能够利用高次DDO结构的基本单位所固有的差分信息泄漏规律构造高概率差分路径。因此，使用高次 DDO结构时应当综合考虑到高次 DDO结构与算法中其它编码环节、圈子密钥与数据的结合方式的相互影响，从而消除高次 DDO结构和其它编码环节在差分分析下所存在的固有信息泄漏规律。

表6 MD-64算法攻击结果对比情况

［1］ Sareh E， San L， Ivica N， et al.. The resistance of PRESENT-80 against related-key differential attacks［J］. Cryptography and Communications， 2014， 6（3）: 171-187.

［2］ Yuseop L， Kitae J， Changhoon L， et al.. Related-key cryptanalysis on the full PRINTcipher suitable for IC-printing［J］. International Journal of Distributed Sensor Networks， 2014（1）: 1-10.

［3］ Wen L， Wang M Q， and Zhao J Y. Related-key impossible differential attack on reduced-round LBlock［J］. Journal of Computer Science and Technology， 2014， 29（1）: 165-176.

［4］ 詹英杰， 关杰， 丁林， 等. 对简化版 LBLock 算法的相关密钥不可能差分攻击［J］. 电子与信息学报， 2012， 34（9）: 2161-2166. Zhan Y J， Guan J， Ding L， et al.. Related-key impossible differential attack on reduced round LBlock［J］. Journal of Electronics & Information Technology， 2012， 34（9）: 2161-2166.

［5］ Chen J G and Atsuko M. Differential cryptanalysis and boomerang cryptanalysis of LBlock［C］. The International Cross Domain Conference and Workshops 2013， Regensburg，Germany， 2013: 1-15.

［6］ Jongsung K， Seokhie H， Bart P， et al.. Related-key boomerang and rectangle attacks: theory and experimental analysis［J］. IEEE Transactions on Information Theory， 2012，58（7）: 4948-4966.

［7］ Takanori I， Yu S， and Jiageng C. Related-key boomerang attacks on KATAN32/48/64［C］. Australasian Conference on Information Security and Privacy 2013， Brisbane， Australia，2013: 268-285.

［8］ Ashur T and Dunkelman O. A practical related-key boommerang attack for the full MMB block cipher［C］. Cryptology and Network Security 2013， Paraty， Brazil， 2013: 271-290.

［9］ Moldovyan A and Moldovyan N. A cipher based on data-dependent permutation［J］. Journal of Cryptology， 2002，15（1）: 61-72.

［10］ Moldovyan A， Moldovyan N， and Sklavos N. Controlled elements for designing ciphers suitable to efficient VLSI implementation［J］. Telecommunication System， 2006， 32（2）: 149-163.

［11］ Nguyen Hieu-minh， Do Thi-bac， and Ho Ngoc-duy. New SDDO-based block cipher for wireless sensor network security［J］. International Journal of Computer Science and Network Security， 2010， 10（3）: 54-60.

［12］ Sklavos N， Moldvyan N A， and Koufopavlou O. High speed networking security: design and implementation of two new DDP-based ciphers［J］. Mobile Networks and Applications-MONET， 2005， 10（1/2）: 219-231.

［13］ Moldovyan N， Sklavos N， and Moldovyan A. CHESS-64， a block cipher based on data-dependent operations: design variants and hardware implementation efficiency［J］. Asian Journal of Information Technology， 2005， 4（4）: 323-334.

［14］ Bac Do-thi， Minh Nguyen-hieu， and Duy Ho-ngoc. An effective and secure cipher based on SDDO［J］. International Journal of Computer Network and Information Security， 2012，4（11）: 1-10.

［15］ Chang-Hoon L. Security analysis of block cipher MD-64 suitable for wireless sensor network environments［J］. Journal of Korea Navigation Institute， 2011， 15（5）: 865-869.

［16］ Jinkeon K， Kitae J， Sang-Soo Y， et al.. Related-key attack on the MD-64 block cipher suitable for pervasive computing environments［C］. International Conference on Advanced Information Networking and Applications Workshops，Fukuoka， Japan， 2012: 726-731.

［17］ Biham E， Dunkelman O， and Keller N. Related-key boomerang and rectangle attacks［C］. EUROCRYPT 2005，Aarhus， Denmark， 2005: 507-525.

郭建胜： 男，1972年生，教授，研究方向为密码学与信息安全.

崔竞一： 男，1992年生，硕士，研究方向为分组密码设计与分析.

罗 伟： 男，1987年生，助理工程师，研究方向为分组密码设计与分析.

刘翼鹏： 男，1992年生，硕士，研究方向为分组密码设计与分析.

Related-key Rectangle Attack on MD-64

Guo Jian-sheng①②Cui Jing-yi②Luo Wei③Liu Yi-peng②
①（Science and Technology on Information Assurance Laboratory， Beijing 100072， China）②（The PLA Information Engineering University， Zhengzhou 450001， China）③（The PLA Unit 78179， Chengdu 611830， China）

The security of MD-64 block cipher under related-key rectangle attack is studied. Firstly， when the weight of input difference is 1， the differential properties of high order DDOs （Data Dependent Operations） and SPN structures are researched. By the differential properties of high order DDOs and the high probability differential of SPN structures， two related-key differentials are constructed. Secondly， a full round related-key rectangle distinguisher of MD-64 is constructed by connecting two related-key differentials. Thirdly， a related-key rectangle attack is proposed on MD-64， and 32 bits of the master key is recovered with 262related-key chosenplain-text， 291.6encryptions of MD-64 block cipher， and a storage complexity of 266.6Byte. The success rate of this attack is about 0.961. Analysis results show that MD-64 can not reach the design target under related-key rectangle attack.

Block cipher； Cryptanalysis； MD-64 algorithm； Related-key rectangle attack

China Postdoctoral Science Foundation（2014M562582）

TN918.1

A

1009-5896（2015）12-2845-07

10.11999/JEIT150049

2015-01-08；改回日期：2015-09-15；网络出版：2015-11-01

*通信作者：郭建胜 tsg_31@126.com

博士后科学基金（2014M562582）