规模条件下协同运输的集散路线优化问题

翁克瑞，诸克军，刘 耕

（中国地质大学 经济管理学院，武汉 430074）

协同运输是指将多个企业的运输任务合并于少数路段集中运输后，利用规模经济节约运输成本。在当前我国物流企业数量多、规模小、运输满载率低以及空载率高的背景下，协同运输是整合物流资源、提高运输效率、降低运输成本的有效手段[1]。如图1的运输任务选择图2的协同运输方案，合并于少量路段而节约成本。一个从节点i到j的运输任务称之为O-D流i→j；若大量的O-D流整合于路段（k，m），且（k，m）获取规模经济、产生运输成本折扣，则称（k，m）为中枢路段，如图2的路段（B，E）。协同运输的主要优势在于中枢路段大规模运输带来的整合效益，这也暗示了中枢路段必须满足规模条件：即中枢路段上汇集的流量必须达到规定的规模数量。

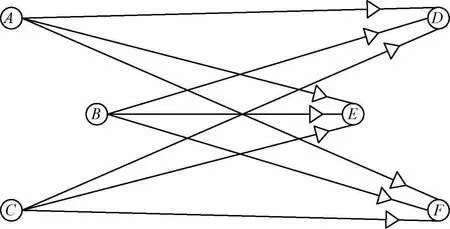
图1 运输任务Ⅰ

图2 协同运输路线

目前，关于协同运输的O-D流路线优化研究主要集中于轴辐式网络设计问题（Hub-and-Spoke Network Design Problem，HASNDP），该问题的一般定义为：要求所有的O-D流都经过1个或2个枢纽站，枢纽站之间的所有路段均具备运输成本折扣的中枢路段，如何选择枢纽站、安排O-D流的集散路线使总成本最小。HASNDP最初由O'Kelly提出，O'Kelly建立了一个二次规划模型，并给出了两类启发式算法。近年来，许多研究仍在改进模型与求解方案[2-5]；同时，一些学者研究HASNDP扩展问题的模型及算法[6-10]。然而，HASNDP的研究存在一个严重的假设缺陷：只要O-D流全部经过枢纽站，则枢纽站间的所有路段都可以获得规模经济和成本折扣。这一假设并不符合某些实践，许多学者研究[4，11-14]发现：枢纽站之间的某些路段可能并未增加流量，不具备规模条件。如图3所示，HASNDP将选择G、H、I为枢纽站，并假定G、H、I之间的所有路段都存在运输成本折扣，形成的O-D流路线如图4所示。实际上，图4中路段（G，H）并未增加流量，不具备规模优势，可见现有研究受假设条件的限制，忽略了协同运输的规模条件。

图3 运输任务Ⅱ

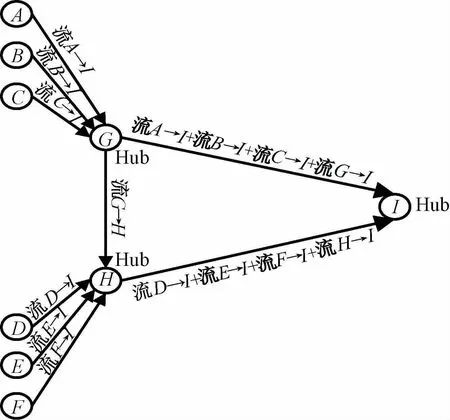
图4 轴辐式网络

因此，本文研究规模条件下的协同运输集散路线优化问题（Collaborative Transportation Route Optimization with Lower Bound Flows，CTROLBF）：给定的中枢路段集合，要求中枢路段上汇集的流量必须达到规定的上限，O-D流在满足绕道距离约束下如何选择直通运输、单点中转或两点中转的路线（称集散路线），使得总成本最小？除规模条件外，协同运输的另一重要缺陷是增加的绕道距离，如对图1的运输任务A→D来说，图2的路线A→B→E→D距离显然大于A→D的直通距离。本文希望绕道运输的距离在某个可以承受的范围以内，于是要求O-D流的路线满足绕道距离约束。

1 模 型

给定的连通网络G（N，A），A为所有边集合，N=｛1，2，…，n｝为所有节点的集合。对任意i≠j，令hij表示节点i到节点j的O-D流，Dij为流i→j的最大运输距离，dkm为路段（k，m）上的单位流量成本，=dik+dkm+dmj为路线i→k→m→j的单位流量成本，Hub Arc为中枢路段集合，Mkm为中枢路段（k，m）要求的最低流量。令决策变量表示流i→j选择路线i→k→m→j的流量。在以上定义下，CTROLBF的线性规划模型P1如下：

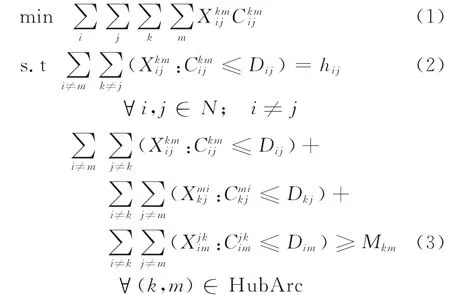
≥0，∀i，j，k，m∈N，k≠j；m≠i目标函数式（1）表示总运输费用最小；约束式（2）表示所有的运输任务都被满足绕道距离约束的路线完成；式（3）表示中枢路段（k，m）上汇集的流量（包括选择路线i→k→m→j，k→m→i→j，i→j→k→m的O-D流量）达到规模条件。模型中，对路线i→k→m→j，要求k≠j与m≠i是为了避免迂回运输，如路线i→j→i→j或i→j→k→j是不允许的；表示流i→j在满足绕道距离约束的路线i→k→m→j上的流量。

2 求解算法

然而，P1是一个大型、复杂的线性规划模型，具备约n4个变量、2n2个约束式。即使只有10个节点，问题的决策变量超过1万个；若有100个节点，则决策变量超过1亿个。为此，对于大规模的CTROLBF，很难在满足时间内获取最优方案。但注意到，模型的约束式数量不多于2n2个，远远小于决策变量的个数。根据线性规划理论，对于2n2个约束的线性规划问题，最多只有2n2个基变量大于0，于是，利用Dantzig-Wolfe分解算法的技术，逐步增加变量。Dantzig-Wolfe分解算法的基本思想是：先选择少数的变量，将原问题分解为容易求解的限制性主问题（RMP）和子问题；求解RMP和子问题，产生其他变量的判别数，如果判别数小于0则加入新的变量，反复迭代直到其他变量的判别数都不小于0为止。

在CTROLBF的最优解中，O-D流i→j会选择少数几条成本最小的出行路径，所以模型P1中变量只有少数几个满足距离约束的路径发生作用。令P表示少数路径的集合。则RMP可表示为模型P2：

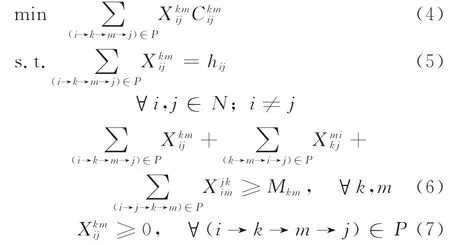
求解RMP得到了原问题的可行方案，但RMP没有考虑所有的出行路径，所以需要判断其他路径能否节约成本。Dantzig-Wolfe分解算法利用列生成的思想，计算出行路径i→k→m→j的判别数为

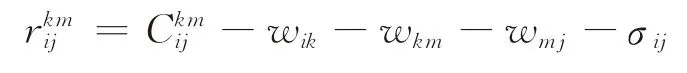
其中，wkm、σij分别为P2中约束式（5）、（6）的对偶变量。如果≤0，则说明选择路径i→k→m→j可节约成本，将路径i→k→m→j加入P后重新计算RMP。对所有的O-D流i→j，求解以下子问题寻找小于0的判别数（P3）：

并且不同的O-D流相互独立，于是可以按照最短路算法求解P3。在满足距离约束的条件下，计算所有的O-D流i→j以（ckm-wkm）为边权重的最短出行成本：

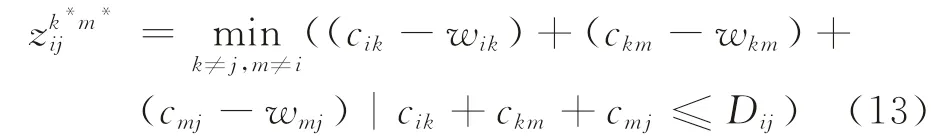
如果＜σij，则说明＜0，将路径i→k*→m*→j加入P。Dantzig-Wolfe分解算法主程序如下：

算法1CTROLBF的Dantzig-Wolfe算法主程序。

（1）产生初始路径集合P（由算法2得到）；

（2）求解模型P2，并得到约束式（5）、（6）的对偶变量wkm、σij，以及出行成本Z；

（3）对所有的O-D流i→j，按式（13）计算以（ckm-wkm）为边权重的最短出行成本；

（4）对所有的O-D流，如果＜σij，则P=P∪（i→k*→m*→j）；

（5）判断是否达到程序终止条件：对所有的O-D流i→j，如果所有的≥σij，则结束程序，更新出行路径与出行成本Z；否则，返回（2）。

在算法1中，本文的初始路径集合P必须满足：①路段最低流量限制；②可安排所有的O-D流路线；③满足出行距离约束。满足以上3个条件才可以保证求解RMP得到可行解，产生过程如算法2。

算法2生成初始路径集合P。

（1）初始化，令Rkm=Mkm表示剩余未满足的流量规模；Tij=hij表示尚未分配的流量，P=Ø。

（2）对所有的路段（k，m），当Rkm＞0时，如果Tij≥0且cik+ckm+cmj≤Dij且i≠m；j≠k，则P=P∪（i→k→m→j），

如果仍然存在Rkm＞0的路段，则说明问题无可行解，退出程序。

（3）对所有O-D流i→j，如果Tij＞0，则P=P∪（i→i→j→j），Tij=0。计算结束。

算法2中，步骤（2）保证中枢路段汇集的流量超过Mkm，步骤（3）保证所有剩余的O-D流被分配。算法结束时，已检查完所有的路段（k，m）与O-D流i→j，说明当前的路线集合P已经满足最低流量限制，并安排了所有O-D流的出行路线。

3 计算实验

本文在VS2008上用C#编写算法进行计算实验，使用Thinkpad x61笔记本电脑，配置主频2.1GHz的Core2处理器与3GB内存；实验中，直接调用Gurobi（著名优化软件）求解模型P2。测试实例来自于OR-Library的AP数据包（http：//people.brunel.ac.uk/～mastjjb/），该数据包提供了澳大利亚200个城市间的邮包流量、距离等数据。在国内外文献中，AP数据包是此类问题算法测试的著名平台，提供了hij、cij等参数。然而，AP数据包没有Dij、Hub Arc与Mkm的数据。本实验中，令Dij=1.5dij，Hub Arc=｛（k，m）|k≠m并且（k+m）为4的整数倍｝；如果（k，m）∈Hub Arc，则Mkm=βhij，并且（k，m）可以获取0.8的成本折扣。这一实验设定可以保证中枢路段上的流量至少是原来直通流量的β倍，并且路线距离不超过原来直通距离的50%。另外，本次实验以AP数据包的前15，20，25，30，60个节点为对象，实验中分别考虑β取值1.4，1.5，1.6的3种情况。

为了分析本文的算法绩效，还运用Gurobi的单纯形法求解模型P1，与算法1进行比较，如表1所示。实验显示，算法1的计算效率明显优于Gurobi，其平均计算时间不到后者的4.63%，且都得到了最优解。此外，当问题规模达到（或超过）100个节点时（此时模型P1的变量数量超过1亿个），Gurobi算法由于规模过大而无法求解模型P1（提示“error 10001”），而算法1耗费约70 s时间得到最优解。

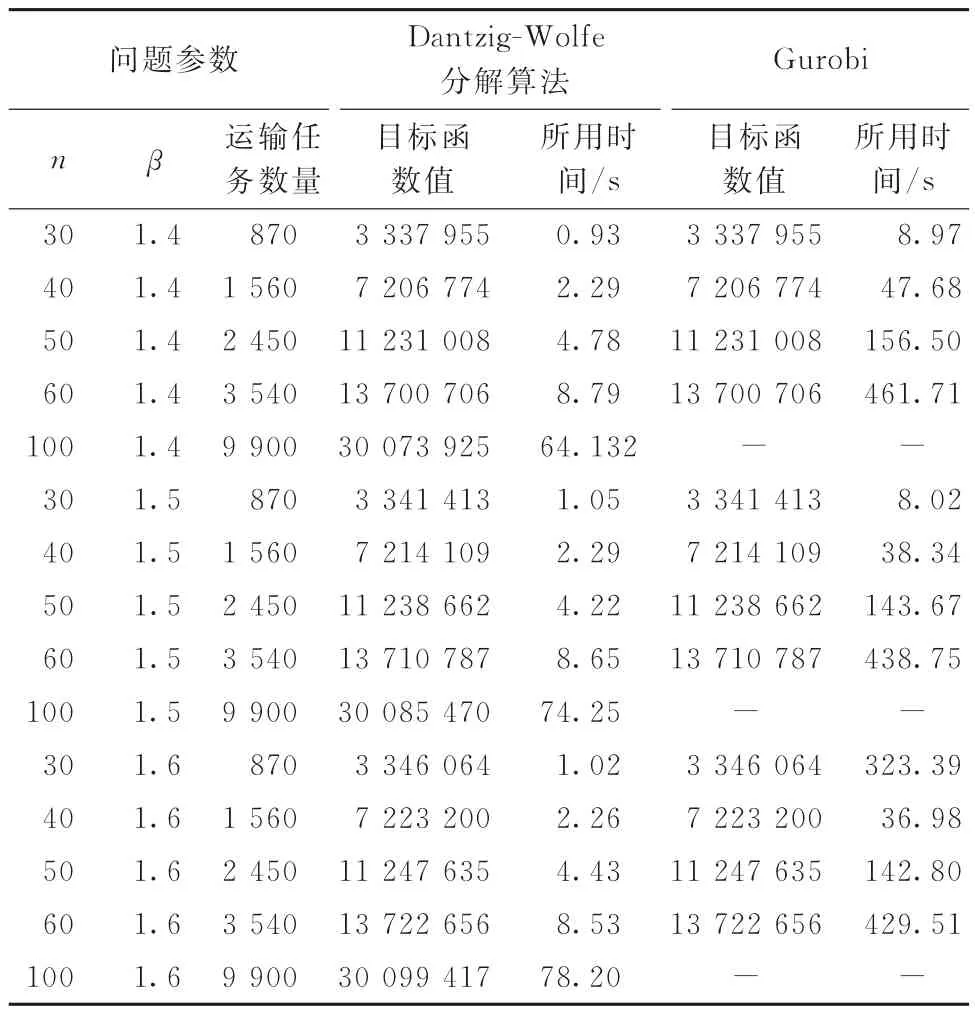
表1 AP 数据包算法实验结果

4 我国中枢航线网络应用实例

航空运输是协同运输的重要应用领域，其原理是：通过中转、合并航线运输，构建中枢航线网络，提高“中枢航线”的飞机满载率，降低单位运输成本。然而，只有当运量达到一定规模条件时，中枢航线（航空运输中的中枢路段）才能体现规模经济。基于《中国交通年鉴》、《从统计看民航》中我国82个城市间客运量（hij）、运费（cij）等数据，这一小节研究带规模条件的中国中枢航线网络设计问题。翁克瑞[4]的研究显示，如果中枢航线满载率从65%提高到95%，则单位运输成本可以降低30%。于是，令中枢航线的最低流量，即中枢航线的流量必须超过原来直通流量的1.46倍；并令中枢航线可以获取0.7的运输成本折扣。同时为减少绕道飞行距离，要求中转飞行距离不超过直通飞行距离的30%，即Dij=1.3dij。Hub Arc选取翁克瑞[4]的研究结论：在不同的航空枢纽港数量下，北京、上海、广州等城市之间的航线为中枢路段的集合。最后，将相关数据代入算法1的程序，计算结论如表2所示。表2中，第4列节约费用=直通运输成本-目标函数值，其中，直通运输成本为我国82个主要城市直航网络的年运输费用为[4]

计算结果显示，算法1能够在5 s内快速求解这一大规模实例；考虑规模条件后，中枢航线网络仍然能够有效地提高我国航空运输效率，年节约80亿元左右的费用；选择9个航空枢纽港是更好的选择；加入乌鲁木齐后问题无可行解，说明乌鲁木齐由于地理上处于我国版图边缘无法在1.3dij的绕道限制内吸引非新疆城市的流量，同时，新疆的其他城市流量不足以使与乌鲁木齐关联的中枢航线（中枢路段）流量增加30%，因此考虑规模条件与绕道距离约束后乌鲁木齐难以成为国内航空中转站（枢纽港）。

表2 规模条件下中国中枢航线网络设计问题计算结果

5 结语

传统的协同运输研究忽略了中枢路段的规模条件，而适当的流量规模是协同运输降低成本的基本条件，为此本文研究规模条件下的协同运输路线优化问题。构造了CTROLBF的线性规划模型和Dantzig-Wolfe分解算法。实验显示，算法表现出了非常好的计算绩效，能够快速得到较大规模实例的最优解。最后，也将模型与算法应用于我国中枢航线网络设计问题。结论显示，算法仍然能够在很短的时间内求解这一大规模问题，并得到最优解；考虑规模条件后，基于协同运输的中枢航线网络能够为我国航空运输节约大量成本。然而，本文只考虑了一种流量规模和折扣效果。很多时候，就如小节1某物流公司的报价一样，流量-运费常常表现为分段线性函数关系，不同的流量等级产生不同的折扣效果。于是，流量-运费分段线性函数下的协同运输路线集散优化问题将成为下一步的研究内容。