面向换乘行为的城市公交客流分配及应用

曾 鹦 ，李 军，朱 晖

（1.成都市社会科学院 经济所，成都 610023；西南交通大学2a.经济管理学院；2b.服务科学与创新四川省重点实验室，成都 610031）

如何提高公共交通的客运能力与服务质量，以保持现有的公交用户与吸引其他更多的出行者选择公共交通已成为缓解城市交通拥堵最根本和最有效的措施，作为公共交通规划的关键技术之一，同时也是交通需求分析和交通运营管理中最重要的一环，公交客流分配问题近年来已引起众多学者的关注和重视[1-3]。

公交客流分配问题是指在公交网络结构和有关参数（运输能力、频率和车头时距分布）已知的情况下，通过模拟乘客在公交网络中的路径选择行为，推导出乘客在不同线网布局下的分布情况，从而得到各公交路段（或公交线路）的客流量和其他指标，据此用以指导实践[4-5]。该问题的表象是乘客的宏观出行现象，其结果是获得公交系统内各公交路段（或公交线路）的客流量和其他指标，其核心则是如何描述乘客在公交网络中各个OD对之间的路径选择行为，其目的是为了了解各OD对之间的客流量在公交网络中各线路上（各公交路段上）的流动情况，并据此为公共交通线网规划和场站布局提供重要的理论依据。因此，从本质上来看，公交客流分配模型就是在乘客路径选择的基准之上做出某种假设而进行的分析和求解[6]。

早在上世纪六七十年代，公交客流分配问题就受到了众多学者的重视和关注：Dial等提出了“主干线路路段”概念；Chriqui等提出“公交共线”概念，解决了乘车点或换乘点如何选择合适的吸引线路集问题，但得到的解并不是全局最优解；自上世纪80年代起，随着人们对考虑拥挤效应的公交客流分配理论研究的逐步深入，均衡概念被引入到公共交通客流分配研究领域，文献[7-9]中的研究都是基于确定型用户均衡概念而建立的经典客流分配模型；文献[10-15]中则是在随机用户均衡的基础之上建立的客流分配模型；需要特别强调的是，在考虑车辆容量约束的前提之下，文献[16-18]中分别建立了随机用户均衡客流分配模型，但各自的侧重点有所不同：文献[16]中强调动态性，文献[17]中基于可靠性，文献[18]中明确考虑了不舒适度，这些研究均属于平衡客流分配模型的研究范畴。

为了使客流分配研究能更好地贴近实际，近几年来关于非平衡分配原则的相关研究逐步被重视：Teklu等[19]巧妙地基于随机过程方法建立了考虑严格安全容量限制的客流分配模型；Rouhieh等[20]基于马尔科夫决策过程的公共交通系统自适应路径选择模型；Kurauchi等[21]采用吸收马尔科夫链方法，考虑线路容量限制以及未能成功搭乘吸引线路集合中第1辆到达车辆的概率，建立共线条件下的客流分配模型；Hazelton等[22]对基于马尔科夫链的交通分配模型的相关计算给出了详细分析，并对其鲁棒性进行了分析。

综上所述，现有关于平衡和非平衡的公交客流分配研究取得了较快的进展和重要的成果，为本文研究奠定了基础，但这些研究大多并未考虑换乘对公交客流分配造成的影响，也就忽视了由换乘带来的出行成本增加而引起的乘客路径选择的多样性和复杂性。而目前大城市中“城外居住，城内上班”现实需求导致的出行距离不断增长而引起公交半径的增加，有相当部分居民出行需通过中途换乘才可到达目的地，这就使得理论研究与生活实践有一定的脱离，为了使客流分配模型能更好地贴近实际，有必要考虑换乘对公交客流分配造成的影响。因此，本文结合公交网络的特殊性，提出了符合乘客路径选择行为的广义公交路径定义，并在此基础上，重点分析了乘客的路径选择行为符合马氏决策过程的“无后效性”，详细给出路径选择过程中涉及的状态-行动空间及状态转移概率，建立了基于马尔可夫链的非平衡公交客流分配模型，并设计了相应的求解算法。最后，运用成都市部分公交网络的实际运营数据对模型和算法进行实例验证，并根据分配结果对相关参数进行了敏感性分析。

1 关键概念与问题描述

公交网络由站点及连接站点的线段组成（线段是指相邻2个站点之间的部分），每条线段都有一组公交线路（以后简称线路）经过，每条线路均有一定的发车频率和服务类型，不同线路之间可能存在部分相同的线段，乘客只能在站点上下车或换乘其他线路。

对于大规模公交网络而言，任意OD对之间连通的路径通常有多条，但乘客并非考虑所有路径，也不会总是单一地选择最短路径，如图1所示。乘客有可能选择直达路径r0（换乘0次），也有可能选择需要换乘1次的路径r1，在某些情况下甚至可能选择需要换乘2次的r2。部分站点离乘客的出发地较近，部分站点离乘客的目的地相对较近，部分站点可搭乘的线路相对较多，这些也都是影响乘客路径选择行为的关键因素。

图1 共线情况下的乘客路径选择

通常情况下，乘客被认为是目标导向的理性个体，在面临不同的交通环境时，有其各自不同的行为目标和行为准则，出行过程中他们不仅需对当前所处环境作出判断与估计，还需对未来的状态（如如果需要换乘，则应考虑选择在哪个站点下车更便捷或更省时）进行预估，以求达到非合作情况下的个人目标最优（如最小化总出行成本、最大化在约束时间内到达的概率等），这就导致整个交通系统状态的不确定性和难以预测性[23]。在这个实际背景下，基于换乘站点提出符合乘客路径选择行为的广义公交路径定义，研究考虑换乘行为的城市公交网络客流分配问题，具有较强的理论意义和实践价值。

2 理论分析及建模

2.1 广义公交路径定义

为避免降低可行换乘路径的搜索空间，本文综合考虑同步换乘（在下车站点即可搭乘需换乘的线路）和非同步换乘（乘客通过步行一段距离换乘的情况），将一定步行距离内可能换乘的多个站点抽象为1个站点对公交网络进行拓扑建模，不同距离下的非同步换乘站点如图2所示。

图2 非同步换乘站点

针对公交网络的特殊性，结合本文提出的换乘站点含义，定义符合乘客路径选择行为的广义公交路径为乘客从起点到达终点所选择的换乘站点序列（简称路径）。称路径上相邻2个换乘站点之间的部分为公交路段（简称路段），路段通常包含1条或多条不同的线段。

简单公交网络与广义公交路径分别如图3、4所示。由原来7条线路（l1，l2，…，l7）编码的公 交网络经由路径编码后，仅有3条路径即可清晰描述：经过站点s1和s4的路径r3，经过站点s1、s2和s4的路径r4，经过站点s1、s3和s4的路径r5。由路径编码的公交线网更加简单明了，对于大规模公交网络而言，该优势将更加明显。

图3 一个简单的公交网络

图4 广义公交路径

2.2 马尔科夫链的适用性

公交出行不同于个体交通（自驾车）出行，其自由度相对较小。通常情况下，尤其对常乘客而言，在每次出行之前乘客都会对当次出行有一定的计划和预期，如根据各自的出行目的、出行距离及为出行预留的约束时间等，选择相应的起点站、换乘站以及终点站等。根据广义公交路径定义可知，公交出行实际上是一组使得乘客从公交网络的各个起始节点经由换乘节点到达终点的规则集合，因此，公交路网中客流量的分配过程，可看成是乘客从公交路网中的起点站出发，在各换乘站点按照一定的转移概率选择可行公交线路，最终到终点站的过程，该过程从广义上来说满足马氏过程的无后效性。下面以乘客一次完整的公交出行（从家到工作地点的公交出行）为例对此过程进行数学描述和证明。

以乘客的地理位置转移为切入点，如从家转移到起点站，从起点站转移到换乘站，从换乘站转移到终点站等，在这一系列转移过程中，乘客总是位于如图5所示的这7个相互排斥但总体完备的状态集合中的元素之一，且在每个状态下都将面临一组可能的行动，如表1所示，当处于“在家”状态时，面临出发时间和起点站的选择，决策的执行使得乘客的状态从“在家”通过步行或其他方式转移到状态“位于起点站”，该状态转移对应图5中虚线框圈出的部分，表1列出了与图5中7个状态对应的所有可能的行动空间。需要特别指出的是，本文重点考察乘客的换乘行为，当乘客到达某一预期或预定的换乘站点时，无论在此之前的选择如何，都不会对乘客在此换乘站点换乘哪条公交线路向目的地前进产生影响，这并不意味着之前的选择不重要，而是当前选择较之前的选择对未来结果的相对影响更大，且在到达换乘站点之前的决策对当前结果的影响可通过乘客到达该换乘站点的时间和到达该换乘站点已支付的票价来体现。

图5 乘客路径选择状态转移图

表1 乘客公交出行过程中的状态及对应的行动

综上分析，可将乘客的路径选择过程视为一个随机过程，记为｛X（t），t∈T｝，令x0=在家，x1=向起点站行进，x2=站点等候，x3=公交车内，x4=换乘站点，x5=终点站，x6=到达目的地，其状态空间为E，对

且X（t）在已知条件

下的条件分布函数只与X（tn）=xn有关，而与

无关，即条件分布函数满足以下条件概率分布等式：

因此，基于乘客的换乘行为，从广义上来说，给定乘客过去的状态x0，x1，…，xn-1和现在的状态xn（即到达换乘站点），将来状态xn+1的条件分布独立于过去的状态，且只依赖于现在的状态（目前所处的换乘站点），即乘客的路径选择行为满足马氏过程的无后效性，即｛X（t），t∈T｝为马尔科夫链。

2.3 基于马尔科夫链的公交客流分配模型

2.3.1 客流量的确定 对于给定的公交网络G（N，A），S为站点集合（si∈S），假设起始站点为p个，终点站为q个，中间换乘站点（不包括起终点站）为n-p-q个，则乘客在整个公交网络中各站点之间的一步转移概率矩阵为

在定义了一步转移概率矩阵P后，m步转移概率为处于状态i的过程在m次转移后处于状态j的概率

由C-K方程（切普曼-柯尔莫哥洛夫方程）可知

记P（n）为n步转移概率的矩阵，由式（2）可得P（n+m）=P（n）P（m），特别地，P（2）=P（1+1）=PP=P2，故由归纳法可知

因此，矩阵p的m次幂矩阵为

乘客通过选取各自的可行线路到达终点站，式（4）中，

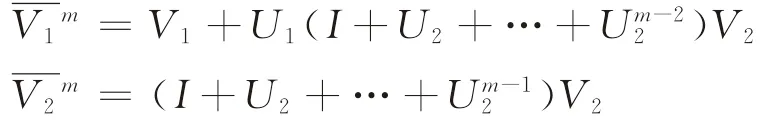
Pm的分块矩阵中的元素（si，sj）为由起始站点si出发的乘客量经过m次转移（即m次换乘）到达站点sj的概率，初始阶段乘客位于各自的出发点，故m=0时，P0=I。若公交路网中所有乘客可行路径的换乘次数最多为M-1次（即路段数目为M），则有=0，那么，由各起始站点so产生的客流量到达各中间换乘站点的概率为[24]。

矩阵G中的元素（si，sj）为由站点si出发的客流量通过换乘站点sj的概率，由换乘站点的选择概率和与之相关联的路段选择概率相乘便可得到乘客该次出行被选路段的选择概率。因此，公交路网中路段（si，sj）的客流量为

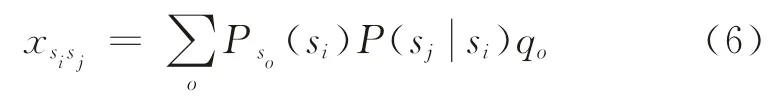
式中：Po（si）为由站点so出发的客流量通过站点si的概率；为乘客由站点si转移到站点sj的概率；qo为由站点so出发的客流量。

2.3.2 广义公交路径下的转移概率 现实生活中，尤其是大城市，“城外居住，城内上班”的现象十分常见。据此，本文选取早高峰期时段的一个多源单汇的公交网络进行研究。根据广义公交路径定义，建立公交路网中由站点si途经路段（si，sj）到达站点sj的一步转移概率函数为[24]

式（7）～（9）中，θ为给定的与路况相关的常数；Rsisd为由站点si到终点站sd的广义路径集合；Rsjsd为由站点sj到终点站sd的广义路径集合；tsisj为路段（si，sj）的行驶时间为由站点si到终点站sd的可行路径第r条路径的广义出行成本为由站点sj到终点站sd的可行路径第r条路径的广义出行成本。

由于

故式（7）给出的转移概率满足非负和归一化条件。对于OD对sosd间乘客的某次出行，在已知出行路径r的所有路段选择概率条件下，r的选择概率为

由式（10）可知，由转移概率得到的路径选择概率与Logit配流模型的路径选择概率是一致的，需要说明的是，式（7）为前向条件转移概率，对起始站点没有任何约束，仅指定了一个唯一的终点站sd，故该转移概率适用于多源单汇的公交路网，也就能满足目前大城市“城外居住，城内上班”的居民出行需求分析。而对于单源多汇的公交路网，有如下的后向条件转移概率定义：

3 模型求解

为了计算转移概率中的Lsisd、Lsjsd、Lsosi和Lsosj，针对一个n个站点的公交路网定义一个n×n矩阵A，如果站点si和站点sj之间有公交线路通过，则Asisj=exp（-θtsisj）；否则，Asisj=0，故式（12）成立。

式中：为由站点si通过n条路段到达站点sj的所有路径集合为中第r条路径的广义出行成本，同理可得

显然，如果路网中任意两站点之间的最多路段数目为M，则有AM+1=0。因此，式（9）的计算就等价于求解以下矩阵系列的和，即

值得注意的是，当广义公交路径定义下的公交路网存在回路时，则路网中至少有2个站点之间的可行路径数目为无穷大，由此，式（5）或式（14）中的最长路径的路段数目M则为无穷大，故有

针对目前“城外居住、城内上班”的现实情况，下面着重分析多源单汇的公交路网，即对起始站点无约束而终点站相同的公交网络（q=1），A矩阵具有如下特殊形式：

式中：

根据转移概率定义，有

综上分析可知，针对多源单汇的公交路网客流分配算法只需计算（n-p-1）×（n-p-1）的逆矩 阵[I-A2]-1，与 直 接 计 算[I-A]-1和[I-U2]-1相比，计算量将大大减少，下面给出具体的算法步骤：

（1）如果站点si和站点sj之间有公交线路通过，则Asisj=exp（-θtsisj）；否则，Asisj=0，据此构造A矩阵，然后由式（14）和式（16）计算L矩阵；

（2）由式（7）、（11）中选择相应的一步转移概率定义式，据此计算一步转移概率矩阵P；

（3）再由式（5）或式（17）得到G矩阵；

（4）若已知或通过需求分析获取OD出行量，由式（6）求得各路段上的交通量。

值得一提的是，若针对一般的多源多汇公交路网，根据分解原理，可将其分解为若干个多源单汇或单源多汇的子路网，这样一来，式（7）、（11）所定义的转移概率同样也能适用。

4 应用算例

现实生活中，尤其是早晚高峰，城市公交网络客流量大，换乘量也大，因此，本文选取成都市如图6所示的6条公交线路：7路下行、28路下行、37路下行、56路下行、62路下行和101路下行，以九里堤公交站到新南门汽车站、西门车站到红星路口和红星路口到西门车站的出行为例，对模型和算法进行验证，通过实际调研和分析可合理假设各路段阻抗值，如表2所示。

图6 用于实例分析的真实公交网络

表2 各路段阻抗

各有效出行路径描述如下：

（1）从九里堤公交站出发，乘坐56下行，经7站到西门车站下车，在西门车站换乘62下行，经10站抵达新南路站，向西北方步行221 m到达新南门汽车站；

（2）从九里堤公交站出发，乘坐101下行，经11站到红星路口站下车，向西南方步行246 m在桂王桥南站换乘28下行，经2站抵达新南门汽车站；

（3）从西门车站出发，乘坐37下行，经8站即可抵达红星路口站；

（4）从红星路口站出发，乘坐7下行，经9站即可抵达西门车站。

将九里堤公交站、西门车站、红星路口以及新南门汽车站分别编码为O、1、2、D，令W=e-θ，如果站点si和sj之间有公交线路通过，则=；否则，=0，据此，构造图6的 矩阵为

则有：

由式（22）可得西门车站和红星路口的选择概率：

由式（19）、（20）计算矩阵：

各站点之间的一步转移概率可由式（7）分别求得：

由式（17）可求得各换乘站（西门车站、红星路口）的通过概率为：

若从九里堤公交站出发的交通量为Q，则各路段客流量可通过式（6）进行计算。

下面运用成都市公交的实际运营数据（数据概况见附录）来检验模型和算法的可行性和有效性，对成都市IC卡消费数据进行统计分析，可合理假设各公交线路2012-06-12的客流量，如表3所示。

表3 以各公交线路2012-06-12的客流量作为各路段的客流值

据式（23）计算各路段客流值，对参数θ进行敏感性分析，考察不同θ取值情况下的客流分配结果（θ=1，θ=2，θ=10，θ=+∞），并对结果做出合理的解释和说明，详情如表4和图7所示。

由图7可知，即便是不同的θ取值，各路段客流分配的预测趋势都是和实际情况较相符的，θ值越大，乘客对路网的熟悉程度越高，分配结果越接近实际，这也是很合理的，从而能从一定程度上验证模型和算法的可行性和有效性。

表4 各路段客流分配结果

图7 参数敏感性分析

5 结语

本文针对中国大城市“城外居住，城内上班”的工作生活模式与公交网络的特性，基于换乘站点，提出了符合乘客路径选择行为的广义公交路径定义，将马尔科夫决策过程与乘客的路径选择行为联系起来，证明了由转移概率得到的路径选择概率与广义路径下的Logit配流模型的路径选择概率是一致的，为解决考虑换乘问题的客流分配问题找到了较好的突破口。本文研究为公交网络规划、城市公交网络设计及优化等提供了一定的理论基础。但是，实际问题的复杂化和模型的抽象化使得本研究存在一些不足之处，若能将GPS数据与IC卡消费数据进行匹配，准确掌握各个时段各个路段的客流量，在此环境下，研究考虑换乘行为的公交客流分配问题更具现实指导意义，深入分析和研究该问题是下一步将要进行的工作。

附录

（1）成都市公交数据概况。截至2012年初，成都市公交集团运营路线已达到323条，成都中心城区平均每天服务乘客达到373万人次，高峰时段的日均载客量已经突破400万大关，IC卡发卡量也由85万张激增至600多万张，中心城区日均出行的分担率已经从2007年的14.7%上升到目前的24.18%。

（2）公交数据库基本表的字段说明。成都市IC卡消费数据库中各个字段表征的含义如附表1～4所示。

附表1 公交卡的基本类型

附表2 公交卡充值数据表

附表3 刷卡消费数据表

附表4 车载GPS数据表