考虑通货膨胀的两层次滞后支付的易逝品订购策略

林晓伟，周熙登

（1.闽南师范大学 商学院，福建 漳州 363000；2.南昌工程学院 工商管理学院，南昌 330029）

在当今的市场环境中，滞后支付（或信用支付）扮演着非常重要的角色，企业采用滞后支付策略，不仅可以促进销售，降低库存水平，而且能够提高市场份额，与此同时，顾客可以很快地获得商品或服务，并且不用立即支付任何费用。

基于滞后支付策略的库存问题引起了许多学者的关注，并取得了不少的研究成果。Goyal［1］首先提出了允许滞后支付的EOQ模型，但是该模型假设采购成本等于销售价格且未考虑变质性商品的情形，随后，许多学者对该模型进行了多方面的扩展。Chu等［2］考虑了变质产品情形下的EOQ模型；Aggarwal等［3］则进一步考虑了变质率为指数分布形式下的库存模型；Jamal等［4］和Chang等［5］进一步研究了滞后支付情况下，变质产品在允许缺货条件下的订货策略；Sarker等［6］研究了变质产品滞后支付条件下的最优支付时间问题。

以上文献仅考虑单层次滞后支付情形下的订购策略。Huang等［7］首先建立了两层次滞后支付策略下的EOQ模型，模型假设供应商提供给零售商一个滞后支付期限M，接着，零售商给顾客也提供一个滞后支付期限N（N＜M），研究了零售商的最优订货策略；之后，Huang［8］对Huang等［7］模型进行拓展，考虑了零售商库存存储空间约束；Huang［9］则构建了两层次滞后支付条件下EPQ模型；在此基础上，Liao［10］构建了具有指数变质率商品的两层次滞后支付EOQ模型；Jaggi等［11］提出了需求依赖付款期限的两层次滞后支付EOQ模型；Thangam等［12］构建了需求同时依赖付款期限和零售价格的两层次滞后支付易逝品定价订购模型。

在现实市场环境中，当批发商有较强的决策权或主导权时，对上游供应商，采取货款完全滞后支付策略，对下游零售商，则采取部分货款滞后支付策略，Huang等［13］在此情况下，构建了两层次滞后支付的EOQ模型；Ouyang等［14］以订购数量作为一个决策因素，构建了滞后支付的EOQ模型；Thangam等［15］探讨了两层次滞后支付策略下两货栈最优定价订购模型；Yen等［16］从更实际的角度出发，认为零售将所获得的销售额立即支付所欠货款，并构建相应模型；Huang［17］研究了变质产品两层次滞后支付条件下的最优支付时间问题。

近年来，特别是当前世界性的金融危机背景下，由于大幅度的通货膨胀和随之而来的货币购买力的迅速下降，各国的经济状况都发生了翻天覆地的改变，资金或费用的时值是时刻变化着的，通货膨胀和资金的时间价值的深远影响也不可能再被忽视。因此，在库存系统的库存管理决策过程中，必须考虑费用的时值对订货策略的影响。最早将费用时值引入库存模型中的当属Buza-cott［18］，在各种价格策略下，Buzacott讨论了通货膨胀条件下的EOQ模型，Misra［19］研究了考虑费用时值的EOQ模型。此后，文献［20-22］中进一步研究了通货膨胀条件下的变质性商品的库存模型。Liao等［23］考虑了通货膨胀和货币时间价值对库存的影响，以总成本为目标函数，构建了两层次滞后支付易逝品库存模型，未考虑部分滞后支付情形。

本文在Liao等［23］的基础上，以批发商利润最大化为目标，构建两层次部分滞后支付易逝品库存模型，使模型更接近于实际情况，并给出了零售商在上述情况下的最优订货周期和最优订购数量的计算方法，从而进一步丰富了信用支付条件下的库存控制理论。

1 模型所用的符号与假设

1.1 模型所用符号

λ—年需求率

K—批发商每次订货的固定费用

h—单位商品单位时间的库存保管费用

c—单位商品的购买费用

s—单位商品的销售价格，其中c＜s

Ik—单位库存单位时间的支付利息

Ie—单位库存单位时间的收益利息

R—关于货币时间价值的贴现率

T—库存周期长度（决策变量）

I（t）—t时刻的库存水平

θ—商品的变质率，假定是一个常数，且商品变质后无残值（0＜θ＜1）

M—供应商允许批发商购买费用滞后支付期

N—批发商允许零售商购买费用滞后支付期，且M＞N

TPH1（T）—T≤N时，该库存系统总利润

TPH2（T）—N≤T≤M时，该库存系统总利润

TPH3（T）—M≤T时，该库存系统总利润

1.2 问题假设

（1）备运期为0。

（2）不允许缺货。

（3）补货率趋于无穷大，即补货是瞬时完成的。

（4）系统运行在无限计划期内。

（5）零售商在购买商品时，必须支付一定比例α的购货款项，在期限N结束时，支付剩余的款项；在期限M之前，批发商将所得收入以利率Ie存入银行挣得利息，在期限M结束时，若库存中的商品还未销售出去，批发商以利率Ip向供应商支付利息。

2 模型的构建

根据以上的分析与假设，在每个补货周期初，即t=0，Q单位商品到达批发商库存，由于销售，以及商品变质的原因，库存将在T时刻变为0，至此一个订货周期结束，然后整个过程重复进行。

显然，在0≤t≤T时，库存水平由于需求和变质而下降，故表示库存水平变化的状态方程为

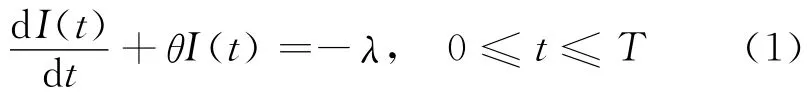
利用边界条件I（T）=0，以上等式可得

于是，每个周期的订货量为

根据上述假定可知，一个订货周期内批发商库存系统的利润函数由以下部分组成。

（1）每个周期固定订购费用为

（2）每个周期的库存成本净现值为

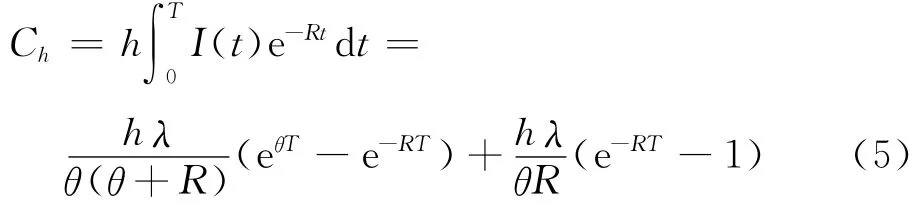
（3）每个周期的购买成本为

（4）每个周期赚取的销售收入的净现值可分为3种情形。

①T≤N。零售商在购买商品时必须支付一定比例α的购货款项，在期限N结束时必须支付其余款项，因此，批发商销售收入的净现值为

②N≤T≤M。同理，零售商在支付比例α的购货款后，剩余的款项在期限N支付给批发商，由于销售没有结束，在［N，T］之间，零售商需要支付全部款项，故批发商销售收入的净现值为

③M≤T。这种情形与N≤T≤M相同，因此，批发商销售收入的净现值为

（5）同理，每个周期所赚取的利息净现值也可分为3种情形。

①T≤N。零售商在购买时就要求支付一定比例的款项，因此，从销售开始，批发商就可以持续地利用销售收入赚取利息，由时刻0～T，获得的利息净现值为。由时刻T～N，利用在销售区间［0，T］内得到的部分销售收入赚取利息，其净现值为。由时刻N～M，即零售商支付剩余的购货款项后，批发商利用整个销售收入赚取利息，其净现值为。因此，由时刻0～M，批发商共赚取的利息净现值为

②N≤T≤M。既然N≤T，由时刻0～M，批发商共赚取的利息净现值为

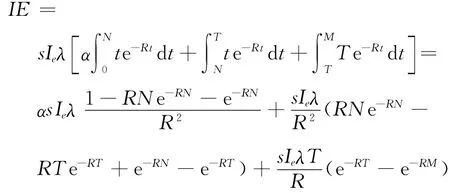
③M≤T。由于M≤T，批发商赚取的利息由两部分组成：由时刻0～N，批发商持续地利用销售收入赚取利息，其净现值为；由时刻N开始，零售商在购买时必须支付全部款项，其净现值为。因此，由时刻0～M，批发商共赚取的利息净现值为

（6）同理，每个周期所支付的利息净现值也可分为3种情形。

①T≤N。批发商允许零售商滞后支付期N，小于滞后支付期M，此时应支付给供应商的利息为0。

②N≤T≤M。同理，此时应付的利息也为0。

③M≤T。在这种情形下，因为销售周期T大于允许固定的滞后支付期M，所以批发商不能在滞后支付期M结束时支付全部款项，因此，由时刻M～T，批发商需要支付剩余库存中商品的利息，其净现值值为

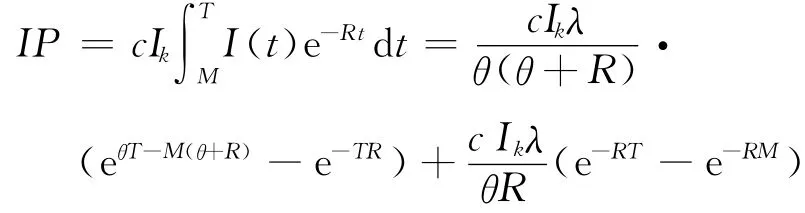
综上所述，批发商每个周期的利润函数为：

经过化简，计算可得：

式（7）～（9）的未来所有现金流的净现值为：

容易验证，

TPH1（M）=TPH2（M），TPH2（N）=TPH3（N）所以TP（T）在区间（0 ，+∞）上是连续的。

本文要解决的问题是在允许购买款项滞后支付的情形下，以求得批发商获得利润最大时的最优订购策略，下面对上述模型进行分析求解。

3 模型求解

由极值存在的必要条件，T的最优值一定满足

因此，可得

式中：

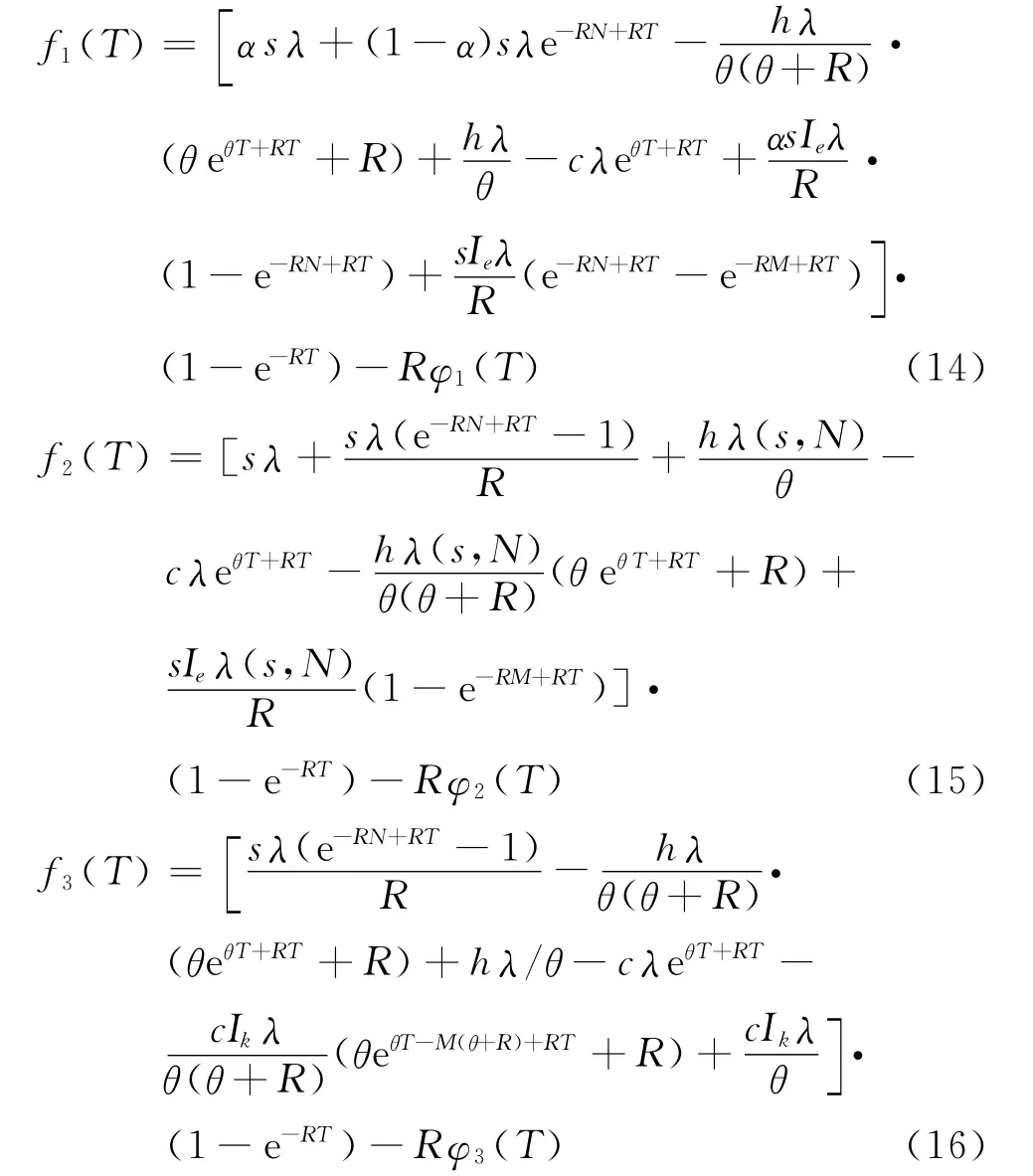
首先给出关干函数TPHi（T）最优解的一个性质定理。

定理1

（2）若f2（0）＞0，则TPH2（T）在区间（0，）内严格递增，而在区间（，+∞）内严格递减，即TPH2（T）在（0 ，+∞）内于处取得最大值。

（3）若f3（0）＞0，则TPH3（T）在区间（0，）内严格递增，而在区间（，+∞）内严格递减，即TPH3（T）在（0 ，+∞）内于处取得最大值。

证明见附录A。

根据定理1，已获得TPHi（T）的最优值T*，由式（14）～（16），可得：

为简化表达，不妨设

由于f2（T）在（0，+∞）内严格单调递减，故有Δ1≥Δ2，下面的定理可以找到模型的最优解T*。

定理2

（1）如 果Δ1＜0且Δ2＜0，TP∞（T*）=TP∞（），因此，T*=；

（2）如 果Δ1＞0且Δ2＜0，TP∞（T*）=TP∞（），因此，T*=；

（3）如 果Δ1＞0且Δ2＞0，TP∞（T*）=TP∞（），因此，T*=。

证明见附录B。

4 数值与算例

例1设s=20，c=10，λ=2 000，M=0.2，N=0.1，R=0.08，h=3，A=100，α=0.7，θ=0.05，Ie=0.1，Ik=0.15，经计算，可得

且

利用定理1可知，批发商库存系统的最优订购周期为T*==0.132 5，所以系统的最大利润为TP*=239 000。调整M和N，可得到其他结果，如表1所示。

表1 M和N的变化对最优订货策略的影响

例2设s=20，c=10，λ=2 000，M=0.7，R=0.08，h=3，A=100，Ie=0.1，Ik=0.15，α=0.7，θ=0.05，分析了滞后支付期N的变化。

表2 N的变化对最优订货策略的影响

例3在例1的基础上，考察购买付款比例α和商品变质参数θ的变化对最优订货策略的影响，结果如表3、4所示。

表3 α的变化对最优订货策略的影响

表4 θ的变化对最优订货策略的影响

表2～4中的数据显示，随着滞后支付期限N的增加，最优订货周期、最优订货量和利润随之减小；而零售商购买付款比例α的增加，最优订货周期和最优订货量随之减小，利润随着增加，这说明，滞后支付期限N和零售商购买付款比例α的变化对系统制定最优订货策略具有一定的影响。另外，随着商品变质参数θ的增加，系统的最优订货周期、最优订货量以及最优利润都在随之减小，这是因为，当商品的变质速度加快时，批发商只有通过减少订货量来尽量避免高变质率所带来的损失，从而使得其利润水平下降，可见，如何控制商品的变质率也是库存管理者必须面对的课题。

5 结论

本文对通货膨胀情形下两层次部分滞后支付库存系统进行研究，其中，供货商提供给批发商购买款项完全滞后支付期，而批发商提供给零售商购买款项部分滞后支付期，并建立了相应的库存决策模型，得出批发商在上述情况下，最优订货周期和订购数量的简单判定方法。

（1）f1（N）=f2（N）＜0，且f2（M）=f3（M）＜0，批发商的最优订货周期为。

（2）f1（N）=f2（N）＞0，且f2（M）=f3（M）＜0，批发商的最优订货周期为。

（3）f1（N）=f2（N）＞0，且f2（M）=f3（M）＞0，批发商的最优订货周期为。

最后，通过实例验证了模型的可行性，得到了与现实相符的结论，随着批发商滞后支付期限N的增加，最优订货周期，最优订货量和利润随之减小；而零售商购买付款比例α的增加，最优订货周期和最优订货量随之减小，利润随着增加，这说明，滞后支付期限N和零售商购买付款比例α的变化对系统制定最优订货策略具有一定的影响。因此，批发商应根据供应商提供的滞后支付期限，灵活制定零售商滞后支付策略，同时，利用供应链的优势地位，对零售商采取部分货款滞后支付策略，需要确定一个合理付款比例，以使得自己的利润最大化。

本文仅研究批发商独立决策问题，以批发商利润最大为目标，忽略了零售商利益损失，批发商在制定滞后支付策略时，即确定付款期限以及付款比例，会对零售商利益产生一定的影响，因此，将进一步研究需求依赖滞后支付期限情形，批发商和零售商组成的二级供应链利益协调问题。另一拓展方向可以放宽假设2，即考虑允许缺货情形下的批发商订购策略。

附录A

定理1的证明

（1）由式（14），可得φ1（T）=TP1（T），f1（T）与有相同的定义域和相同的符号，进一步对f1（T）求导，可得

如果f2（0）＞0，易知f2（T）在区间（0 ，+∞）内存在唯一的零点（设为），因此，TPH2（T）在（0 ，+∞）内于处取得最大值。

如果f3（0）＞0，易知f3（T）在区间（0 ，+∞）内存在唯一的零点（设为），故TPH3（T）在（0，+∞）内于处取得最大值。

附录B

定理2的证明

（1）如果Δ1＜0且Δ2＜0。T*1＜N，＜N＜M，＜M，当T＜N时，TP∞（T）在T=处取得最大值；当N≤T≤M时，TP∞（T）在T=N处取得最大值；当T≥M时，TP∞（T）在T=M处取得最大值。另外，TP1（N）=TP2（N），TP2（N）＜TP2（M），TP2（M）=TP3（M），TP1（）＞TP1（N），根据以上分析，TP∞（T）在T=取得最大值。

（2）如果Δ1＞0且Δ2＜0。＞N，＞N，＜M，＜M，当T＜N时，TP∞（T）在T=N处取得最大值；当N≤T≤M时，TP∞（T）在T=T*2处取得最大值；当T≥M时，TP∞（T）在T=M处取得最大值。另外，TP1（N）=TP2（N），TP2（）＞TP2（M），TP2（）＞TP2（N），TP2（M）=TP3（M），根据以上分析，TP∞（T）在T*=取得最大值。

（3）如果Δ1＞0且Δ2＞0＞N＞N＞M＞M，当T＜N时，TP∞（T）在T=N处取得最大值；当N≤T≤M时，TP∞（T）在T=M处取得最大值；当T≥M时，TP∞（T）在T*=处取得最大值。另外，TP1（N）=TP2（N），TP2（M）＞TP2（N），TP2（M）=TP3（M），TP3（）＞TP3（M），根据以上分析，TP∞（T）在T*=取得最大值。