基于GSA的ELM电能质量扰动识别方法研究
李斌 韩晓红

摘要:ELM是一个单隐层神经网络,具有良好的泛化和快速学习能力,该算法只需用户调整隐含层节点个数,但该参数的选择直接影响了ELM的性能。文章提出一种新的优化方案,该方案使用GSA优化输入特征子集和隐含层节点数以提高ELM的性能,实验结果表明:该方法在识别电能质量扰动方面更快、更准确。
关键词:GSA;ELM;小波变换;特征选择;万有引力搜索算法;极限学习机 文献标识码:A
中图分类号:TM614 文章编号:1009-2374(2015)29-0015-03 DOI:10.13535/j.cnki.11-4406/n.2015.29.008
1 概述
工业中由于电能质量(Power-Quality,PQ)问题已经造成大量资源的流失,导致PQ问题的主要原因是过多地使用固态开关设备、非线性负载、各种数据处理设备等。这些设备的使用使得PQ信号的相位、频率和振幅发生了畸变,从而进一步导致过热、电机故障、谐波失真等问题。传统上,PQ问题可以通过目测干扰波形,但该方法需要工程师具备一定的专业知识,且需要分析大量数据,因此,有必要开发自动的PQ干扰识别方法。
自动识别方法主要包括两步:特征提取和模式识别。小波变换(Wavelet Transform,WT)可以用于电力信号扰动检测和定位。有学者提出基于WT和人工神经网络(Artificial Neural Network,ANN)的PQ扰动检测方法。参考文献[4]使用支持向量机(Support Vector Machine,SVM)实现信号的识别。然而,SVM需要对复杂的二次规划问题进行求解,涉及高的计算复杂度和时间成本,当数据集较大时,这一缺陷更为明显。参考文献[5]使用ANN实现多分类,ANN通过网络直接把输入数据映射到不同的类,ANN易于实现,更像人类的思维认知,然而,对于大规模问题,ANN缺乏有效的快速学习算法,且存在隐含层神经元个数的选择问题。
极限学习机(Extreme Learning Machine,ELM)是一种新的学习算法,它是一种单隐层前馈神经网络学习算法。相比传统的基于梯度的学习算法,ELM学习速度快,且泛化性能好,同时避免了传统学习方法面临的问题。本文使用ELM进行PQ扰动信号识别,相比其他方法,ELM的优点是用户只需调整隐含层节点数目,但最佳隐含层节点数目的选择可以提高其性能。万有引力搜索算法(Gravitational Search Algorithm,GSA)是一种新的群体优化算法,相比其他优化算法,它具有跳出局部最优解的能力,且易于实现,本文通过GSA优化ELM参数以获得较高的分类精度,同时使用GSA对小波变换后PQ扰动信号进行特征提取,以完成对电能质量扰动信号的识别。
2 方法
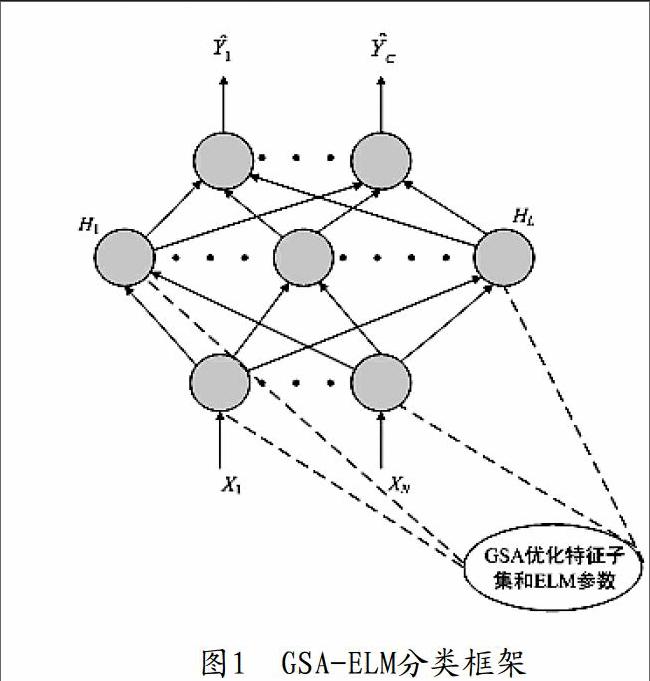
基于GSA的ELM电能质量扰动分类系统首先通过GSA检测最佳特征子集,接着使用GSA估计最佳隐含层节点数,以达到自动优化ELM分类器的准确性。图1为基于GSA的ELM优化分类框架。
图1 GSA-ELM分类框架
给定训练集{Xi,Yi},隐含层节点输出函数为G(W,B,X),Lmax为最大隐含层节点数。
步骤1:通过GSA算法选择最佳输入特征数量(N)和隐含层节点数(L)。
步骤2:随机分配隐含节点的参数(Wi,Bi),i=1,2,……,L。
步骤3:计算隐含层的输出矩阵YH。
步骤4:计算输出权值,是隐含层输出矩阵的广义Moore–Penrose逆矩阵。
2.1 编码
为了有效地利用GSA优化ELM,使用二进制编码表示粒子。表1显示了使用的二进制粒子表示,每个粒子由两部分组成:第一部分包含特征子集f,f选自d个输入特征;第二部分包含隐含层神经元个数。由于位置向量的第一部分用于实现特征选择任务,每个元素为“0”(特征丢弃)或“1”(特征选择)。代表特征值,表示隐含层神经元个数,nc为隐含层神经元的位数。实验使用7位编码方案表示隐含层神经元,13位表示特征值。
2.2 适应度函数
GSA基于适应度函数值评估每一个候选解pi的优劣。适应度函数使用分类精度和特征数作为评估标准。具有较高的分类精度和少的特征数目的粒子具有高的适应度值。式(1)为定义的适应度函数,适应度函数有两个预定义的权重wA和wF,wA代表ELM分类精度acci的权值;wF代表所选择的特征的权值。
(1)
fj为“1”表示第j个特征被选择,“0”表示没被选中,nF是总的特征数。分类的准确性(acc)表示正确分类的百分比,acc通过公式(2)计算,其中cc表示正确分类的数目,uc表示错误分类的数目。
2.3 GSA-ELM系统
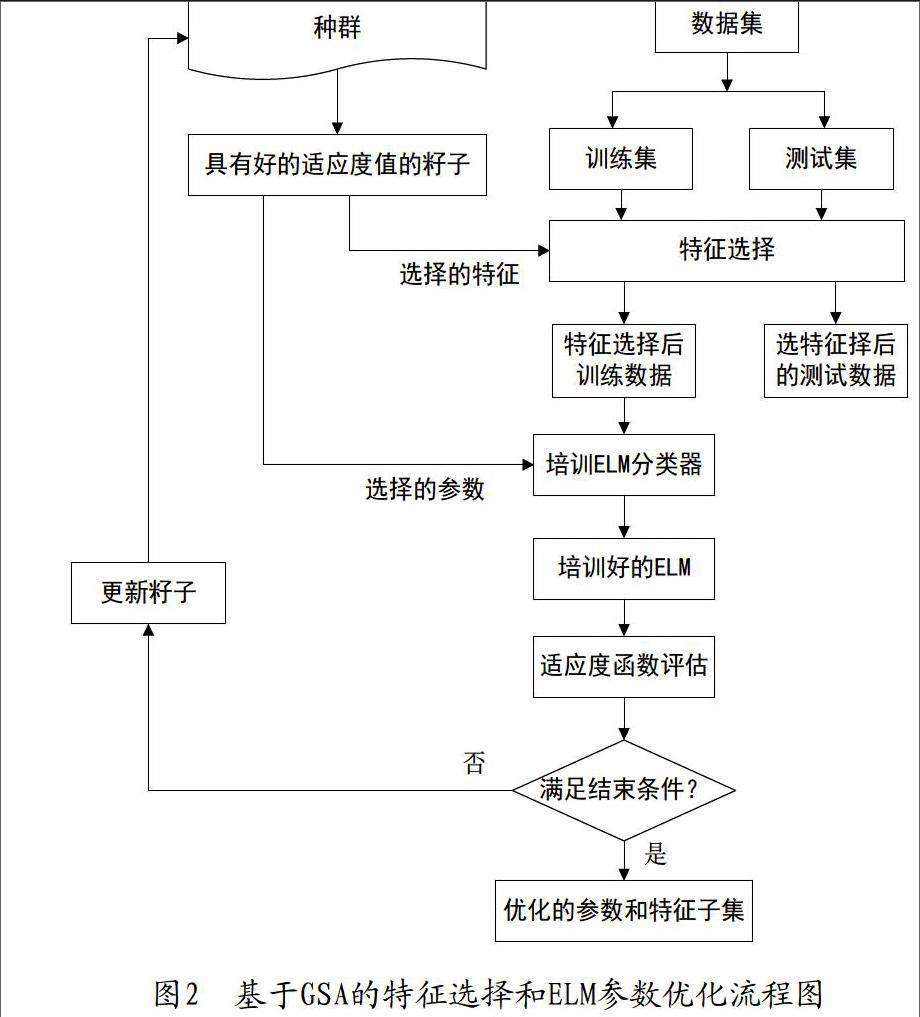
基于GSA的特征选择和ELM参数优化系统描述如下(如图2所示):
步骤1:随机初始化S个粒子的位置及速度矢量vi(i=1,2,…,S)。
步骤2:使用每个粒子pi∈Rd+1(i=1,2,…,S)中的特征子集和隐含层神经元数、训练ELM分类器,并计算相应的适应度函数值fitnessi。
步骤3:更新G(t)、worst(t)、best(t)、,i=1,2,…,S。
步骤4:计算不同方向的合力,计算加速度和速度。
步骤5:使用。
步骤6:使用每个候选粒子pi(i=1,2,…,S),训练ELM分类器,计算相应的适应度函数fitnessi。
步骤7:如果最大迭代次数尚未达到,返回到步骤2,否则转到步骤8。
步骤8:选择群中最佳位置,通过映射的特征子集培训ELM分类器,使用映射的隐层神经元数目建模。
步骤9:使用训练好的ELM分类器对电能质量扰动信号进行分类。
3 实验
本节实验评估提出的GSA-ELM分类系统的性能。使用MATLAB 2013a作为开发平台,实验硬件环境是Intel(R)Core(TM)i5-4440CPU@3.10GHz,3.09GHz 8.00GB内存,操作系统是Microsoft Windows 8。
3.1 数据描述
实验使用9类(C1-C9)不同的PQ干扰事件,数据描述如下:C1表示电压暂降,C2表示电压暂升,C3表示电压中断,C4表示谐波,C5表示频率波动,C6表示振荡暂态,C7表示间谐波,C8表示脉冲暂态,C9表示电压缺口。在MATLAB使用不同参数值的参数化模型产生这9类电能质量信号。
实际中,每个扰动事件的特性会有很大的差异。为了模拟实际,生成100种不同的事件。50个事件用于培训,通过随机变化各种参数生成另外50个事件,用于测试事件的所属类别,使用深度、角度、开始时间和持续时间用于改变事件的不同种类。深度指一个信号的幅度变化,角度代表信号的相移,开始时间是事件开始的时间,持续时间指事件的扰动时间。
根据IEEE,实验中的上述参数在不同的情况下有所变化,对这些样本进行小波变换,分解信号到第十三级。
3.2 基于特征选择和参数优化的扰动分类
GSA算法的种群大小设置为20,隐含层神经元的搜索范围是0~127。准确率权值wA调整到95%,特征集的权值wF设置为5%。表2给出了在特定的迭代下给定神经元个数,获得的最优特征数目和ELM隐含层神经元的数目。
为了评估该方法的有效性和可行性,比较ELM和GSA-ELM的分类准确率,比较结果列于表3。从表3可见,使用基于特征选择和参数优化方法的GSA-ELM分类性能超过ELM的分类性能。
表4给出每个类的精度比较结果,从表4可以看出,使用基于GSA-ELM分类方法,有4种扰动(C1,C5,C6,C7)获得了百分之百的分类精度,使用ELM方法,有2种扰动(C2,C4)获得了百分之百的分类精度。
4 结语
本文提出基于GSA的ELM电能质量扰动识别方法,通过GSA检测可用的最佳特征子集和优化的ELM参数,提高ELM分类器的分类性能。该方法对于提高具有分类能力的PQ监测设备的性能具有巨大的潜力。从所获得的实验结果可以看出,提出的方法可以应用于电能质量扰动信号分类,且该方法的分类能力优于传统的分类方法。
参考文献
[1] W.-M.Lin,C.-H.Wu,C.-H.Lin,F.-S.Cheng.Detection and classification of mul-tiple power-quality disturbances with wavelet multiclass SVM[J].IEEE Trans.Power Deliv,2008,23(4).
[2] H.Eris ti,Y.Demir.Automatic classification of power quality events and dis-turbances using wavelet transform and support vector machines[J].IET Gener.Transm.Distrib,2012,6(10).
[3] A.M.Gaouda,M.M.A.Salama,M.K.Sultan,A.Y.Chikhani.Power quality detec-tion and classification using wavelet-multiresolution signal decomposition[J].IEEE Trans.Power Deliv,1999,14(4).
[4] C.Cortes,V.Vapnik.Support vector networks[J].Mach.Learn,1995,(20).
[5] R.Zhang,G.-B.Huang,N.Sundararajan,P.Saratchandran.Multicategory classi-fication using an extreme learning machine for microarray gene expressioncancer diagnosis[J].IEEE/ACM Trans.Comput.Biol.Bioinform,2007,4(3).
[6] W.Li,C.Chen,H.Su,Q.Du.Local binary patterns and extreme learning machinefor hyperspectral imagery classification[J].IEEE Trans.Geosci.Remote Sens,2015,53(7).
[7] G.-B.Huang,C.-K.Siew.Extreme learning machine:RBF network case,in:Proceedings of the Eighth International Conference on Control,Automation,Robotics and Vision(ICARCV 2004)[J].Kunming,China,2004,(2).
[8] Y.Bazi,N.Alajlan,F.Melgani,H.AlHichri,S.Malek,R.R.Yager.Differential evo-lution extreme learning machine for the classification of hyperspectral images[J].IEEE Trans.Geosci.Remote Sens.Lett,2014,11(6).
[9] E.Rashedi,H.Nezamabadi-pour,S.Saryazdi.GSA:a gravitational search algorithm[J].Inform.Sci,2009,179.
[10] E.Rashedi,H.Nezamabadi-Pour,S.Saryazdi.BGSA:binary gravitational search algorithm[J].Nat.Comput,2010,9.
[11] A.M.Gargoom,N.Ertugrul,W.L.Soong.Investigation of effective automaticrecognition systems of power-quality events[J].IEEE Trans.Power Deliv,2007,22(4).
作者简介:李斌(1985-),男,供职于国网宁夏电力公司信息通信公司。
(责任编辑:周 琼)

