船舶航向模糊自适应云模型控制

邢道奇 龚 铭

（海军工程大学 勤务学院 天津300450）

船舶航向模糊自适应云模型控制

邢道奇 龚 铭

（海军工程大学 勤务学院 天津300450）

［摘 要］为了解决船舶航向云模型控制器驱动参数的自适应问题，将模糊自整定方法引入到云模型控制器设计中，设计了模糊自适应云模型控制器，并进行了仿真对比试验。结果表明，该控制器可以使船舶航向控制在动态和稳态上都具有较好的精度，超调量小、控制效果良好。

［关键词］船舶航向；云模型控制；模糊自适应

引 言

船舶航向控制是船舶控制的一个重要方面，它直接关系到船舶航行的操纵性、安全性和经济性。由于船舶运动具有惯性大、非线性、模型参数不确定以及存在扰动等特点，对系统进行航向控制器设计时会遇到很大困难，简单的PID航向控制器已经不能满足要求。为了解决这一问题，人们将许多先进技术应用到控制器设计中，出现了参数自适用控制器、滑模控制器、鲁棒控制器、智能控制器［1-4］。其中，基于云模型的智能控制技术，是近几年发展起来的，已经成功运用于倒立摆的稳定控制［5］、船舶航向控制［6］、电动机控制［7］等方面，取得了良好的控制效果。

在基于云模型的船舶航向控制［6］中，云模型控制器的驱动系数需用人工方式进行调节，但当船舶在航行环境发生变化或受干扰时，原有的云模型控制器特性不能随之自动作相应变化，将导致控制效果变差，使舵机启动频繁且舵的摆动幅度较大。针对云模型控制器中驱动系数无法自适应的问题，本文借鉴模糊自适应PID控制器设计方法，将模糊控制运用到航向云模型控制中，实现在线动态调整云模型控制器驱动系数。仿真结果表明：航向云模型控制的品质得到进一步改善，有效提高了云模型控制的静态和动态性能。

1 船舶非线性数学模型

根据文献［8］，选择外界干扰下的船舶非线性Norrbin模型：

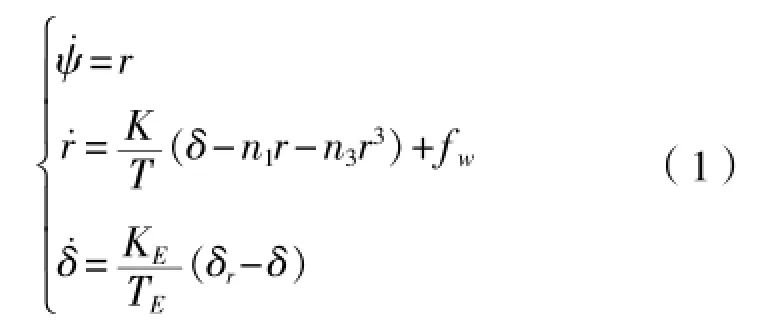
式中：ψ为首向角；r为首摇角速度；为首摇角加速度；K为系统增益系数；T为时间常数；为舵角；为舵转动速度；n1、n3为Norrbin系数；为参考舵角；TE为舵机时间常数；KE为舵机控制增益；fw为外界干扰项。

2 模糊自适应云模型控制器设计

2.1 云模型控制器

（1）云模型概念

设U是一个用精确数值表示的定量论域，C是U上的定性概念。若定量值、x是定性概念C的一次随机实现，且x对定性概念C的确定度是有稳定倾向的随机数［9］：

图1 一维单规则云模型推理

（2）云模型推理［10］

云模型推理通过实现IF…THEN…推理规则，来实现基于语言子集的非线性映射能力。图1为一维单规则云模型推理图。用X条件云发生器CGx和Y条件云发生器CGy来构造单定性规则：IF A THEN B。输入变量x激活不同的X条件云CGx产生不同的μi，然后经过Y条件云CGy产生云滴drop（yij，μi），这些云滴经过加权平均或逆向云输出，可以获得相应的推理结果，完成整个推理过程。

（3）航向云模型控制器

定义航向偏差为：

分别将航向偏差e、偏差的积分值ei、偏差的变化率作为3个一维云模型映射器的输入量，经过云模型不确定性推理，分别得到输出控制量uP、uI、uD，经过驱动系数KP、KI和KD分别放大，并求和作为舵机的控制输入，以实现航向控制。

根据上述方法，参考文献［6］，构建船舶航向控制的结构图（如图2所示）。航向控制器中一维云模型控制器构成，虽类似于传统的PID控制器，但又具有本质区别。

图2 船舶航向云模型控制结构图

2.2 模糊自适应云模型控制原理

设计模糊自适应云模型控制的结构，如图3所示。其中，云模型控制部分完成对航向控制，而模糊整定器则根据航向偏差e和偏差变化率的变化情况，通过模糊推理对云模型器中的驱动系数KP、KI、KD进行在线整定，以达到较好的控制效果。

图3 模糊自适应云模型控制结构图

（1）确定模糊整定器的输入、输出量

输出量：云模型驱动系数KP、KI、KD。

输入、输出量均选用5个模糊集作为其语言值，即｛负大（NB）、负小（NS）、零（ZE）、正小（PS）、正大（PB）｝。

驱动系数的KP、KI、KD作为输出量选用7个模糊集作为其语言值，即｛零（ZE）、小（S）、较小（RS）、中（M）、中大（RM）、较大（RB）、大（B）｝

（2）模糊控制规则设计

驱动系数KP值的选取决定了航向控制的响应速度。增大KP能提高响应速度，减小稳态误差。但KP值过大会产生较大的超调，甚至使系统不稳定。减小KP可以减小超调、提高稳定性，可KP值过小会减慢响应速度、延长调节时间。因此，调节初期应适当取较大的KP值以提高响应速度。在调节中期，KP取较小值，以使系统具有较小的超调，并保证一定的响应速度；而在调节后期，再将KP调到较大值来减小静差，提高控制精度。KP值的模糊控制规则如表1所示。

驱动系数KI在云模型航向控制中，用来调整系统的稳态误差。在调节初期，为防止云模型控制中积分饱和，KI应当取较小值，甚至可以取零；而在调节中期，为避免影响稳定性，KI应当取值适中；而在调节后期，则应增大KI值，以减小稳态误差。KI的模糊控制规则如表2所示。

表1 KP的模糊控制规则表

驱动系数KD在云模型控制中作用在于改变系统的动态特性。在调节初期，应加大微分作用，以获得较小超调甚至避免超调；在调节中期，由于调节特性对KD值的变化比较敏感，因此KD值应适当小一些并应保持固定不变；在调节后期，KD值应减小，以减小被控过程的制动作用并补偿在调节过程初期由于KD值较大所造成的调节过程的时间延长。KD的模糊控制规则如表3所示。

表3 KD的模糊控制规则表

3 仿真研究

3.1 云模型控制器仿真条件

以5 446标准箱系列集装箱船“Cosco Rotterdam”号［11］为仿真对象，进行航向控制仿真研究。

表4 一维云模型参数

分别用五个语言值NB、NM、Z、PM和PB表示一维云模型映射器的输入和控制输出的论域。其中NB为负大、NM负中、Z零、PM正中、PB正大，推理规则如表5所示。

表5 一维云模型定性控制规则表

当船航行速度为24.5 kn（即12.6 m/s）时，K =0.241 9、T = 206.795 8、n1=11.604 9、n3=10.196 6。驱动系数分别取为：KP=10.0、KI= 0.005和KD=15.0，给定初始条件为ψr=10°。

3.2 模糊自适应云模型控制器仿真条件

定义航向模糊整定器输入、输出量的基本论域如下：

航向偏差e的基本论域为：［-18，18］，单位：°；航向偏差变化率的基本论域为：［-3，3］，单位：°/s。

驱动系数基本论域：

KP的基本论域为：［3，15］；KI的基本论域为：［0，0.001］；KD的基本论域为：［5，20］。

为了使控制效果具有可比性，其他初始条件与3.1节相同。

3.3 仿真分析

图4 -图8表示在无外界干扰下得到的控制仿真曲线；图9表示有外界干扰下得到的模糊自适应云模型控制仿真曲线；图10表示未采用模糊整定、有外界干扰下得到的云模型控制仿真曲线。

图4 驱动系数 KP整定曲线

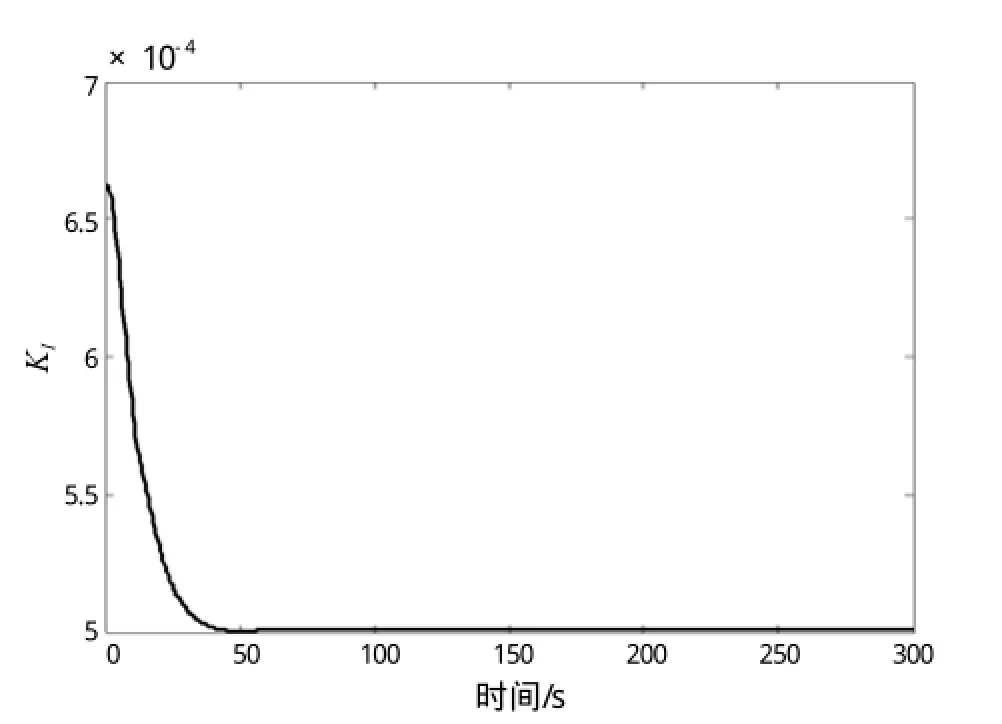
图5 驱动系数 KI整定曲线

图6 驱动系数 KD整定曲线

图7 舵角 δ 曲线对比

图8 首向角 ψ 曲线对比

图9 干扰下模糊自适应控制时的 ψ-δ 曲线

图10 干扰下未采用模糊自适应控制时的 ψ-δ 曲线

其中，图4 -图6分别为云模型驱动系数KP、KI、KD的自适应曲线。从图中可以看出：经过模糊推理，云模型驱动系数在仿真过程中进行了自适应调整，实现了较好的控制效果。通过图7的对比可以看出，经过模糊自整定后，云模型控制器的控制性能有了明显提高，舵角δ响应的幅值由原来的11.8°减小到8.9°；而图7中航向ψ的响应时间却并没有增大，与云模型控制器的控制时间相同，约为51.5 s。从图8的对比分析可以得出：在响应的初期和中期，经过模糊推理，选取较小的驱动系数KP，以防止出现超调；因此出现了响应速度小于未采用模糊整定的云模型控制器，在图中表现为实线在虚线右侧。这也是舵角δ响应的幅值较小的原因。在响应后期，通过减小驱动系数KD，提高响应速度，减小响应时间。在有干扰的情况下，对比图9和图10也可以看出：经过模糊整定的云模型控制器控制性能有了明显提高。总之，通过与原云模型控制器控制性能的比较可以发现，模糊自适应的云模型控制器明显提高了航向控制的效果，具有较强的鲁棒性、较高的稳态精度和更快的响应特性。

4 结 论

云模型控制作为一种新的智能控制方法，在解决具有非线性、随机性、多变量以及强耦合性的系统控制问题方面，体现出较好的控制优势，已经得到广泛应用。本文在航向云模型控制的基础上，引入模糊自整定方法，设计了船舶航向模糊自适应云模型控制器，解决了云模型控制器中驱动参数无法自适应的问题，通过仿真试验验证了新控制器设计的有效性，控制效果良好。

［参考文献］

［ 1 ］ 杜佳璐，郭晨，杨承恩．船舶航向非线性系统的自适应跟踪控制器设计［J］.应用科学学报，2006（1）：83-88.

［ 2 ］ 邢道奇，张良欣．船舶航迹跟踪的滑模控制［J］. 船舶. 2011（5）：10-14.

［ 3 ］ 张显库，关巍．大惯性船舶航向保持的改进简捷鲁棒控制［J］.中国航海，2010（3）：1-5.

［ 4 ］ 卓永强，方祥麟．船舶航向在线自学习智能控制方法［J］.大连海事大学学报，2007（2）：75-79.

［ 5 ］ 李德毅．三级倒立摆的云控制方法及动平衡模式［J］.中国工程科学，1999（2）：46-48．

［ 6 ］ 高键，周岸，李众．船舶航向保持系统的云模型控制研究［J］. 江苏科技大学学报（自然科学版），2008 （5）：11-16.

［ 7 ］ 李志民，卢曦，孙勇，等．同步发电机云模型励磁控制器的设计［J］.电力系统及其自动化学报，2010 （3）：91-95.

［ 8 ］ 杨盐生．不确定系统的鲁棒控制及其在船舶运动控制中的应用［D］.大连：大连海事大学，1999．

［ 9 ］ 李德毅，孟海军，史雪梅．隶属云和隶属云发生器［J］.计算机研究与发展，1995（6）：15-20．

［10］ 高键，姜长生，李众. 一种新的云模型控制器设计［J］.信息与控制，2005（2）： 157-162.

［11］ 沈智鹏，郭晨.大型集装箱船舶运动模糊自整定PID控制［C］//Proceedings of the 7th World Congress on Intelligent Control and Automation，Chongqing，China，2008：356-360．

［中图分类号］TP273

［文献标志码］A

［文章编号］1001-9855（2015）03-0042-06

［收稿日期］2014-09-17；［修回日期］2014-11-06

［作者简介］邢道奇（1980-），男，博士，讲师，研究方向：海上补给技术、海洋结构物应用工程。龚 铭（1978-），男，硕士，讲师，研究方向：海上补给勤务与技术。

On fuzzy adaptive cloud model control of ship course

XING Dao-qi GONG Ming

(Naval Universitg of Engineering, Tianjin 300450, China)

Abstract：In order to solve the adaptability of the drive parameters of the cloud model controller in ship course，fuzzy adaptive model is introduced in the design of the cloud model controller. This paper designs the fuzzy adaptive cloud model controller， and carries out the simulation to compare with experiments. The results show that the new controller can command the ship course with better precision， small overshooting and good control effect under both dynamic and steady conditions.

Keywords：ship course； cloud model control； fuzzy adaptability