“场力做功”的特点都一样吗？

沈志辉

（上海市松江一中 上海 201600）

场是物质存在的两种基本形态之一，存在于整个空间.简单地说，物理学中所说的“场”就是具有某种物理作用的空间.在这个空间里可以测量到反映物体作用的物理量.每一种场都有对应的物理特性或物质属性，例如电磁场对应于电磁特性.电磁场是由具有电磁性的物体产生的，并且只对具有电磁性的物体产生作用.

1 问题的提出

在历史上，场的概念主要是从牛顿提出万有引力定律开始，牛顿理论清晰地告诉人们关于超距作用的思想.牛顿的后继者们在某些方面甚至比牛顿走得更远，在牛顿超距作用理论的影响下建立了不少电磁学理论，如库仑定律、安培环路定理等，这些理论说明了引力、电力、磁力是同类力，是统一的.但牛顿的万有引力定律不要求两个物体接触，这困扰了很多人，包括牛顿本人.

为了合理解释这种超距现象，牛顿的后继者中另外一些人则选择了一条不同的道路，他们把看来像“超距作用”的力看做是靠充满空间的一种介质传递的，这样就把超距作用归并到接触作用的概念之中，这种观点直接导致了“以太”假说的出现.笛卡儿于1644年最先将以太引入科学，并提出了引力的“以太漩涡说”.1820年4月，丹麦物理学家奥斯特发现导体中及其周围空间会发生所谓的“电冲突”，并得出结论：电冲突只能对磁性粒子起作用，奥斯特的发现与牛顿的超距作用理论是矛盾的.1821年9月，法拉第受奥斯特的“电冲突”的启发，历经10年，发现了“电磁感应”现象，提出了“电致紧张状态”和“磁感线”两个概念.在接下来的日子里，麦克斯韦相继发表3 篇论文：《论法拉第力线》、《论物理力线》、《电磁场的动力学理论》，文章指出：场是在一定空间连续分布的，变化的磁场产生涡旋电场，光波就是电磁波等，并明确宣告他提出的理论可以称为“电磁场的理论”.紧接着，赫兹通过实验证实了麦克斯韦电磁理论的正确性…… 现如今，实验已经证明以太是不存在的.于是，人们逐渐意识到物质有两种基本形态：实物和场.而且，我们也知道，物理学的发展，使实物和场走向统一.

所有的场都是可以测量到物理量的空间.每种场只与对应的特性或属性相互作用.场之间没有交叉作用.任何物质之间的相互作用都是依靠相应的场来实现的.如电场、磁场、引力场等.那么，场之间具有这么多的共性，是否意味着场力做功也具有相似的特点呢？这是值得我们研究的话题.本文就是在场的众多共性基础上，探讨一下典型场力做功的特点，从而区分磁力做功拥有不同的一面.

2 典型“场力”做功的特点

2.1 引力场—— 重力做功

物体和地球构成一重力系统，物体所受的重力是系统的内力.现设质量为m 的物体从a 点沿任一曲线acb 运动到达b 点，a点和b 点对所选取的参考平面来说，高度分别为ha和hb，如图1所示.

图1

在位移元ds中，重力G 所做的功是

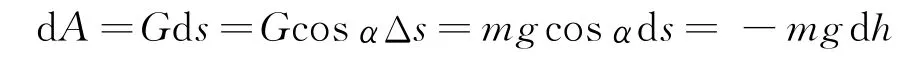
式中

就是在位移元ds中物体上升的高度，所以重力所做的功是

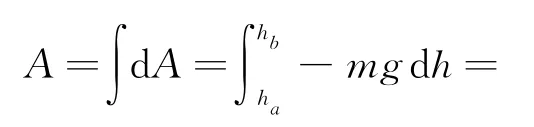
可见物体上升时（hb大于ha），重力做负功（A 小于零）；物体下降时（hb小于ha），重力做正功（A 大于零）.

从计算中可以看出，假使物体从a 点沿另一曲线运动到b点，所做的功仍如式（1）所示.由此可知，重力做功的特点是：做功只与运动物体的始末位置（ha和hb）有关，而与运动物体所经过的路径无关.这个特点也可表述如下：当物体从a 点沿任一闭合路径绕行一周时，重力所做的功为零.具有这种特点的力称为保守力，那么引力场可称之为保守场.

2.2 静电场—— 电场力做功

设在给定点O 处，有点电荷q.现有试验电荷q0在q的电场中从a 点经过任意路径acb到达b点，如图2所示.

在路径中任一点c的附近，取与c极邻近的c′点，从c到c′的位移元为dl，并设c点处的场强为E，可知在dl这段路径上，电场力q0E 所做的功为

式中θ是E 的方向和dl的方向之间的夹角，已知

代入式（2），可得

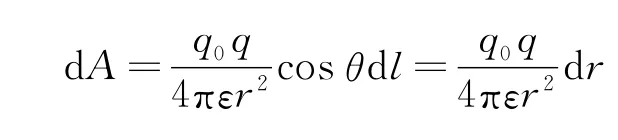
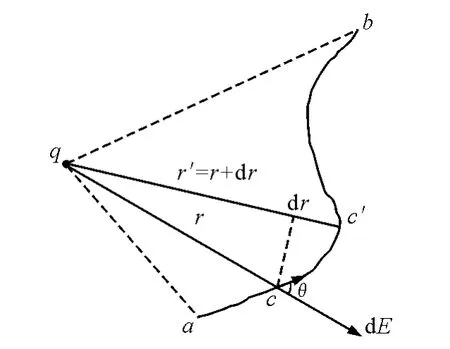
图2

当试验电荷q0从a点移到b 点时，电场力所做的功为

式中ra和rb分别表示从点电荷q所在处到路径的起点和终点的距离.由此可见，在点电荷q 的电场中，电场力所做的功与路径无关，仅与试验电荷电量的大小以及路径的起点和终点位置有关.

任何静电场都可看做是点电荷系中各点电荷的电场的叠加，试验电荷在电场中移动时，电场力对试验电荷所做的功也就等于各个点电荷的电场力所做功的代数和.用数学式表示时，可记作

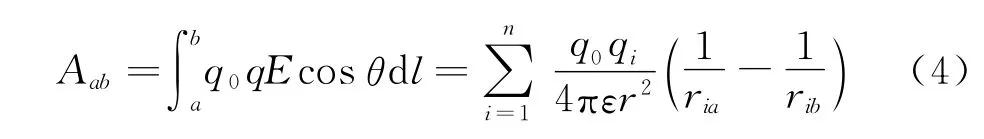
式中ria和rib分别表示从点电荷qi所在处到路径的起点a和终点b的距离.由于每个点电荷的电场力所做的功都与路径无关，所以相应的代数和也与路径无关.因而得出结论：试验电荷在任何静电场中移动时，电场力所做的功，仅与试验电荷电量的大小以及路径的起点和终点位置有关，而与路径无关.这说明静电场力也是保守力，静电场也是保守场.

2.3 稳恒磁场—— 磁场力做功

载流导线或载流线圈在磁场内受到磁力（安培力）或磁力矩的作用，因此，当导线或线圈的位置与方位改变时，磁力就做了功.下面笔者就从一些特殊情况出发，建立磁力做功的一般公式.

2.3.1 载流导体在磁场中运动时磁力所做的功

设有一匀强磁场，磁感应强度B 的方向垂直于纸面向外，如图3所示.磁场中有一载流的闭合电路abcd（设在纸面上），电流I保持不变，电路中导线ab之长为l，ab可以沿着da 和cb滑动.按安培定律，载流导线ab 在磁场中所受的力F，在纸面上，指向如图所示.F 的大小F＝BIl，在力F 的作用下，ab将从初始位置，沿着力F 的方向移动.当移动到位置a′b′时，磁力F所做的功A＝Faa′＝BIlaa′.当导线在初始位置ab 和在终了位置a′b′时，通过回路的磁通量分别为Φ0＝Blda，Φ1＝Blda′，所以磁通量的增量为

可知在导线移动的过程中，磁力所做的功为

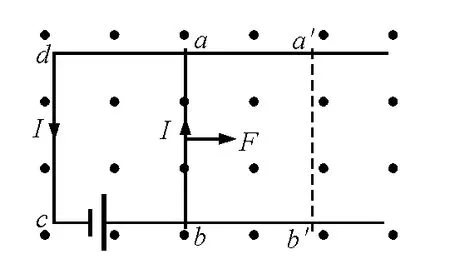
图3

这一关系式说明，当载流导线在磁场中运动时，如果电流保持不变，磁力所做的功，等于电流乘以通过回路所环绕的面积内磁场量的增量；也可以说磁力所做的功，等于电流乘以载流导线在移动中所切割的磁力线数.

2.3.2 载流线圈在磁场中转动动时磁力所做的功设有一载流线圈在匀强磁场内转动，设法使线圈中电流维持不变.现在来计算线圈转动时，磁力所做的功.

图4

如图4所示，设线圈转过的角度dφ，使n与B 之间的夹角从φ 增为φ＋dφ.磁力矩为M＝BILsinφ，所以磁力矩所做的功

式中的负号表示磁力矩做正功时将使φ 减小.因为BScosφ 表示通过线圈的磁通量，而d（BScosφ）就表示线圈转过dφ 后，磁通量的增量dΦ.所以式（5）也可写成dA＝IdΦ.

当上述载流线圈从φ1 转到φ2 时，按dA＝IdΦ，积分后得磁力矩所做的总功

式中Φ1和Φ2分别表示线圈在φ1 和φ2 时，通过线圈的磁通量.

可以证明，一个任意的闭合电流回路在磁场中改变位置或改变形状时，磁力或磁力矩所做的功都可按A＝IΔΦ 计算，亦即磁力或磁力矩所做的功等于电流乘以通过载流线圈的磁通量的增量.

如果电流是随时间而改变的，dA＝IdΦ 仍能适合，但这时磁力所做的总功要用积分式计算

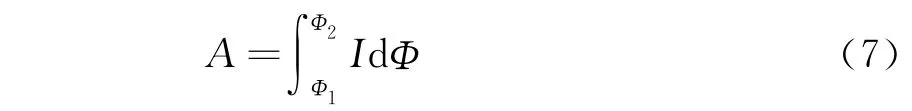
这是磁力做功的一般表达式.

由此可见，磁力做功并不像重力做功、电场力做功那样，看来磁力并非保守力，故磁场并非保守场.

3 为什么磁场不是保守场

与电场相仿，磁场是在一定空间区域内连续分布的向量场，描述磁场的基本物理量是磁感应强度矢量B ，也可以用磁感线形象地图示.然而，作为一个矢量场，磁场的性质与电场颇为不同.

运动电荷或变化电场产生的磁场，或两者之和的总磁场，都是无源有旋的矢量场，磁力线是闭合的曲线簇，不中断，不交叉.换言之，在磁场中不存在发出磁力线的源头，也不存在会聚磁力线的尾闾，磁力线闭合表明沿磁力线的环路积分不为零，即磁场是有旋场而不是势场（保守场），不存在类似于电势那样的标量函数.

在一个物理系统里，假若感受着一个作用力的施加，一个粒子沿某路径从初始点移动到最终点，而此作用力所做的物理功不会因为路径的不同而改变，则称此力为保守力.作用力为保守力，则它满足以下的充要条件对于任何简单的闭合路径，所做的功是零.数学表达式是

在存在保守力的系统中，可以引入和位置有关的能，称之为势能，如电势能、重力势能.另外还可以引入势的概念，并把这样的力场称为保守场，如重力场和电场等.反之，如果一个力做功和路径有关，则称该力为非保守力.有非保守力存在的力场称为非保守场，如磁场等.

定理可以写成

两边乘以qm0（试探点磁荷），就可以得到

也就是磁场力做功与路径有关，因此说稳恒磁场是非保守场.概括的说，由安培环路定理可以看出，磁场中B的环流一般不等于零.综上所述，稳恒磁场的特点与静电场有所不同，静电场是保守场，磁场是非保守场，故“场力做功”确有相似之处，但不尽相同.

1 程守洙，江之永.普通物理学（第4版）.北京：高等教育出版社，1994

2 冯杰.大学物理专题研究（第1版）.北京：北京大学出版社，2011

3 梁灿斌.电磁学（第2版）.北京：高等教育出版社，2004

4 郭硕鸿.电动力学（第2版）.北京：高等教育出版社，1998