一类具有时滞和非单调感染率的传染病模型

王 霞,郭淑利

(信阳师范学院 数学与信息科学学院, 河南 信阳 464000)

0 引言

众所周知,在传染病模型的定性描述中,传染率在其动力学行为中起着非常重要的作用[1-6],并且绝大多数经典传染病模型,通常考虑的是双线性传染率βSI,其中β为每次接触后的有效传染的概率,S和I分别表示易感类和感染类的数量.在文献[7]中,Capasso和Serio引入饱和传染率βSI/(1+αI),α>0;在文献[8]中,Xiao和Ruan首次提到非线性感染率βSI/(1+αI2),α>0,其中βI表示感染疾病的力度,1/(1+αI2)表示当感染类数量很大时,易感类随之产生的抑制效应.

本文在上述研究的基础上,通过构造Lyapunov泛函方法,研究了具有非单调感染率βSI/(1+kI+αI2)的时滞传染病模型:

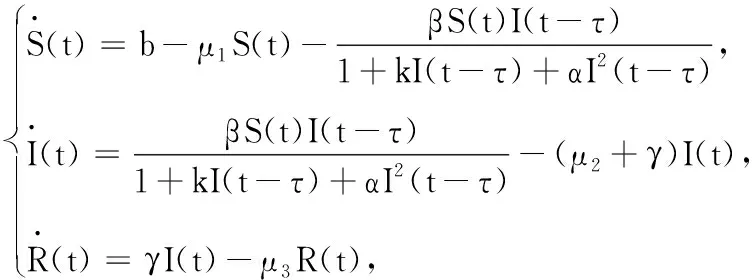
其中:S(t),I(t)及R(t)分别表示易感类、感染类及康复类在t时刻的数量;b为总人口的常数出生率;μ1,μ2及μ3表示易感类、感染类及康复类的死亡率.考虑到生物学意义,假设μ1≤min{μ2,μ3};β为有效接触率;γ为感染个体的自然康复率.非单调感染率βSI/(1+kI+αI2)>0,I≥0,其中k>0,α>0;τ>0表示易感者接触感染者后被感染需要的时间.

1 主要结果

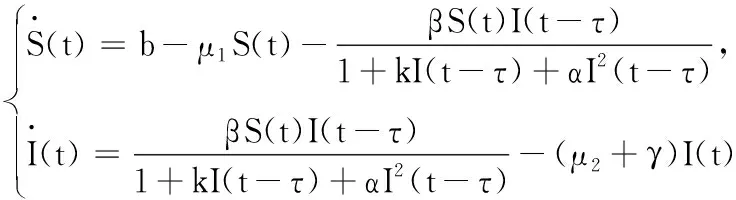
解的性质即可.为此,给出系统(2)的初值

S(0)∈[0,+),I(θ)=φ(θ),θ∈[-τ,0],

(3)

其中φ∈C([-τ,0],[0,+)),C为[-τ,0]到[0,+)连续函数的全体映射组成的空间.

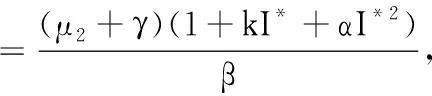
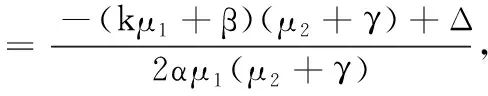
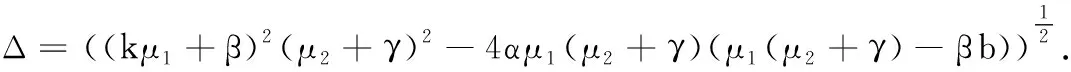
为系统(2)的基本再生数,则容易证明:当R0≤1时,系统存在唯一平衡点E0;当R0>1时,除E0外,系统存在地方病平衡点E*.

引理1 对于系统(2)的任意解(S(t),I(t)),总有

证明令N(t)=S(t)+I(t).注意到μ1≤min{μ2,μ3},因此由系统(2)可得

引理2 设(S(t),I(t))为系统(2)具有初值条件(3)的任意解,则对于所有的t≥0,总有S(t)≥0,I(t)≥0.

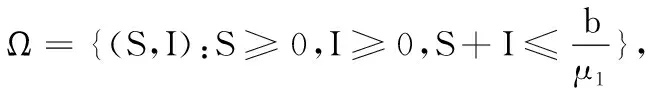
定理1 若R0>1,则地方病平衡点E*是全局渐近稳定的.

证明定义函数

由系统(2),可得

b=μ1S*+βS*f(I*),

(4)

(μ2+γ)I*=βS*f(I*).

(5)

为讨论E*的全局渐近稳定性,定义

以及Lyapunov泛函

注意到h:(0,+)→[0,+)上存在全局最小值点h(1)=0.因此,V(t)≥0.对于所有s∈[0,τ],等号成立当且仅当及

下面分别推导出VS(t),VI(t)以及V+(t)的全导数.为此,有

运用式(4)中表达式替换b,则

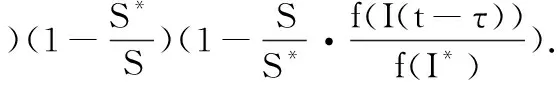
令

则有

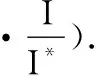
运用式(5)中表达式替换(μ2+γ)I*,则

h(y)-h(z)=y-z+lnz-lny.

(10)

联立方程(8)-(10),则有

通过同时加减表达式ln(xF(z)),可得

F(z)-z+lnz-lnF(z)=

F(z)-z+lnz-lnF(z).

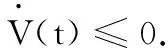
2 数值结果

本节主要运用MATLAB 7.1对文中所得结果进行验证.为此,选取参数b=0.9,μ1=0.15,β=0.1,α=4.6,k=2.9,γ=0.08,μ2=0.82,μ3=0.2,τ=0.25.此时,容易计算系统(2)的基本再生数R0=0.67<1,其无病平衡点E0全局渐近稳定(见图1).

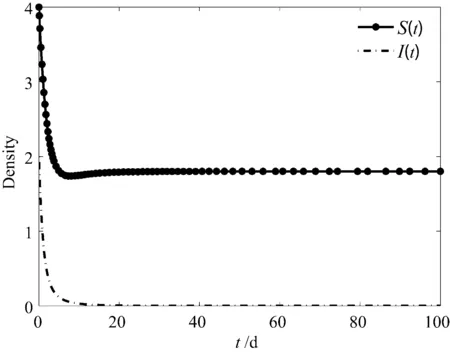
图1 系统(2)平衡点E0的稳定性Fig. 1 Stability of equilibira E0of system (2)

选取参数b=0.9,μ1=0.2,β=0.8,α=4.6,k=2.9,γ=0.08,μ2=0.82,μ3=0.2,τ=0.25,此时,容易计算系统(2)的基本再生数R0=4>1,其正平衡点E*全局渐近稳定(见图2).

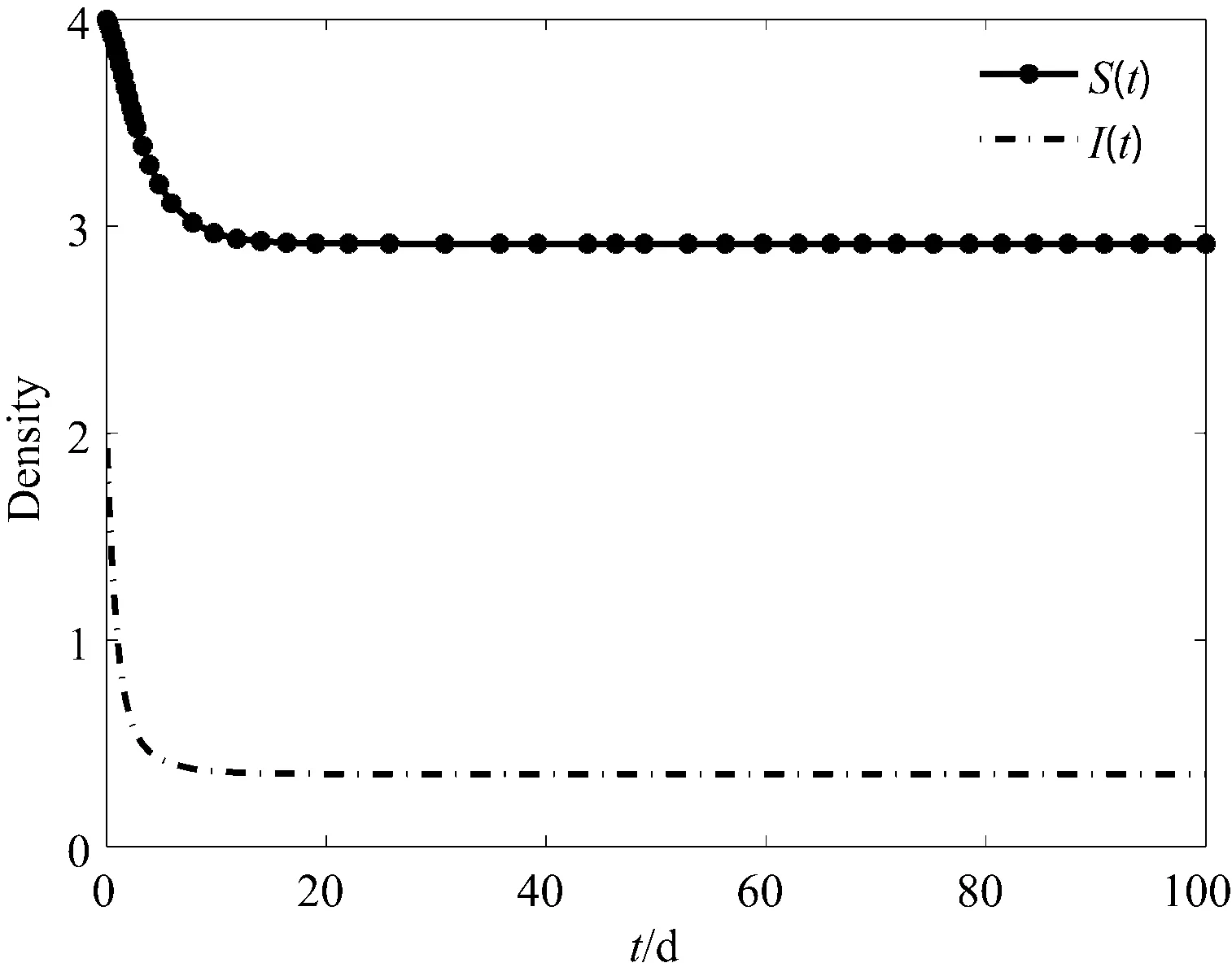
图2 系统(2)平衡点E*的稳定性Fig. 2 Stability of equilibira E*of system (2)

3 结语

基于时滞效应与非单调传染率在传染病控制模型中的重要作用，主要研究具有时滞与非单调传染率的传染病模型，运用Lyapunov泛函方法，得到了当系统的基本再生数大于1时,地方病平衡点是全局渐近稳定的.最后，运用Matlab给出数值结果.