二维Stokes flow快速多极边界元法及截断误差
弓小影,闫涛红,于春肖*
(1. 石家庄经济学院 数理学院,河北 石家庄 050031;2. 燕山大学 理学院,河北 秦皇岛 066004)
0 引言
边界元法是一种精确高效的工程数值计算方法.二维域上边界元法的主要思想是将域内的微分方程转化为边界上的积分方程,使得问题的维数降低一维.通常,转化后的积分方程具有奇异性,为了解决这一问题,陈一鸣等用Galerkin-wavelet法去离散自然边界积分方程[1-2],从而使强奇异性减弱,还提出了一种强奇异积分方程的数值解法.
快速多极算法使边界元法的大规模计算成为现实,并应用于弹性力学、声学等领域[3-6].姚振汉、王海涛引入指数展开的定义[7],得到一种新的展开传递格式,使快速多极边界元中的展开系数和传递关系得以简化.Bapat等通过改进“邻居”和“相互作用列表”的概念来减少多极展开到局部展开的工作量[8].Greengard结合近远场划分准则对二维位势问题的多极边界元方法的多极展开和局部展开的截断误差进行了分析[9].
本文以二维Stokes flow问题为研究背景,在基本解快速多极展开平移的基础上,阐述了改进“相互作用列表”以后的算法是如何在计算多极展开系数到局部展开系数的平移中加速计算的.最后给出了二维Stokes flow问题位移基本解多极展开的截断误差估计式.
1 核函数展开及平移过程
二维Stokes flow问题的边界积分方程一般形式如下:
Tij(x,y)uj(y))dS(y),
其中:下标i,j=1,2;S是求解域的边界;x,y分别代表边界上的源点和场点;uj和tj分别是边界的位移与面力;系数Cij(x)是与边界形状相关的常数;Uij(x,y),Tij(x,y)是二维Stokes flow问题的Kelvin基本解.
位移的复变函数形式的基本解可表达为:
(1)

平面Stokes flow问题位移基本解的多极展开式为:
(2)
其中:z0为源点,z为场点.利用泰勒级数在zc展开,zc靠近场点z,且满足|z-zc|<|z0-zc|,多极展开系数为
(3)
(4)
(5)
其中Sc为积分域.
如果展开点从zc平移到一个新的点zc′时,得M2M平移公式
(6)
(7)
局部展开系数可以通过多极展开系数平移得到,假设zL是距离源点z0非常近的一点,且满足|z0-zL|<|zc′-zL|,在传统多极边界元方法中,有
(8)
其中,Ll(zL)和Kl(zL)为局部展开系数,可以通过M2L平移得到
(9)
(10)
当展开中心从zL移到zL′时,得L2L平移公式
(11)
(12)
2 主要计算步骤及计算效率简析
2.1 主要计算步骤
二维Stokes flow多极边界元方法的主要计算步骤可以分为以下五步:
第一步离散边界,生成树结构.

第三步下行遍历计算多极展开系数的平移,由式(6)和式(7)对每个多极展开系数进行平移,累加得到下一层结点的多极展开系数,依次往下对树结构的l≥2层结点进行计算.
第四步利用式(8)~(10),上行遍历计算局部展开系数.
在这一步,对“相互作用列表”进行改进.在传统算法中,结点x的“相互作用列表”是一组结点y的集合,见图1(a),结点y与x不相邻,但它们的父结点与x的父结点相邻.可以看出,一个结点的“相互作用列表”中最多有27个结点.改进“相互作用列表”,见图1(b),用父结点z代替4个子结点y使结点总数减少到12,这样可以降低所需的存储量,提高计算效率.
第五步由式(11)和式(12)进行局部展开系数的平移,得计算结果.
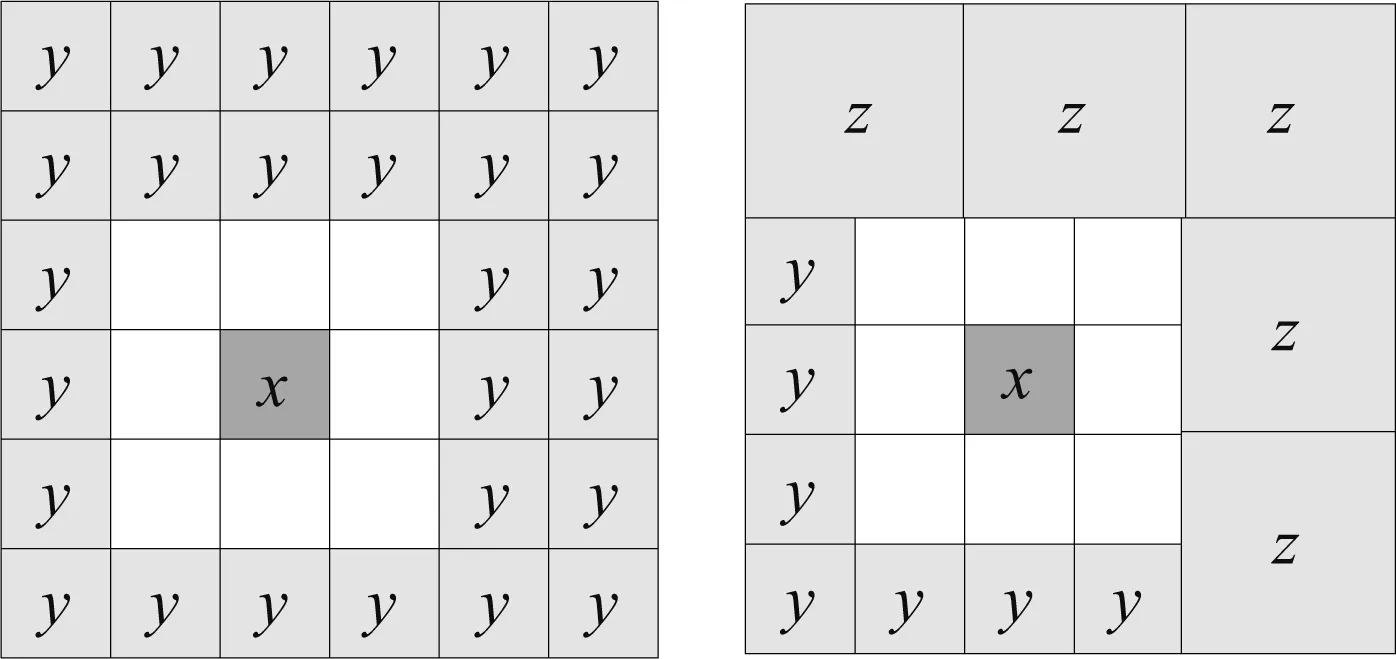
(a) (b)
2.2 改进前后计算效率简析
在二维Stokes flow快速多极算法中,第四步占有主要的计算量.在传统的多极算法中第四步需要最多27次的M2L操作,根据式(7),这27次操作的计算量级为O(27p2),改进“相互作用列表”以后,结点总数减少到12,总的计算量就可以减少到O(12p2),提高了计算效率.
3 多极展开截断误差分析
3.1 近远场划分准则
考虑到计算的需要,在多极展开中,一般不会计算到展开式的无穷多项,而是对展开式截取到有限项,这样就会产生误差,在讨论多极展开的截断误差之前首先给出二维问题近远场划分准则.
定义1 若存在两组点x1,x2,…,xn∈Ox和y1,y2,…,ym∈Oy(见图2)和实数R>0,且
|xi-x0| |yj-y0| |x0-y0|>3R, 则称点集{xi}与{yj}是相互独立的,或者称点集{xi}与{yj}相距足够远. 图2 近远场划分示意 用Ox表示中心在x0,半径为R的圆;Oy表示中心在y0,半径为R的圆.根据三角不等式,对任意yj∈Oy,j=1,2,…,m,满足 ‖yj-x0‖≥2R≥2‖xi-x0‖,i=1,2,…,n. (13) 在进行二维Stokes flow多极边界元方法核函数的展开平移计算时,对于源点z0,区域内点zL满足|zL-z0| 定理1 在二维Stokes flow问题核函数的多极展开式(1)中,当截断项数到p时,产生的误差为 证明将式(1)中二维Stokes flow问题的位移基本解写成 其中, 对于S3,由|z0-z|≤|z0-zc|+|zc-z|,得 z)Ik(z-zc)||t(z)|dS(z)+ (14) (15) 根据近远场的划分准则可得,|z0-zc|≥2R,这样就有ρ≥2,进一步得到 (16) 同理,可得 (17) 于是由式(14)~(17),可得 且 从而由上面的分析可得 证毕. 通过对多极边界元计算量级的分析,说明改进“相互作用列表”以后的算法加速计算的原理.同时,通过对二维Stokes flow问题的位移基本解多极展开的截断误差进行分析,验证了截断误差与截断项数p的选取有关,可由截断项数p控制.
3.2 多极展开的截断误差分析

4 结论

