基尼系数估算数学模型的选择及计算机程序实现
牛晓奇,常保平
(安阳师范学院 a.数学与统计学院;b.软件学院,河南 安阳 455000)
0 引言
随着经济社会的发展,特别是“中原经济区”上升为国家战略后,河南与中西部乃至东部省份在多个领域的竞争日趋激烈,而判断经济社会发展的主要指标是看城乡居民收入增长幅度和生活幸福指数.如何衡量与判断现有收入分配政策公平度,优化收入分配政策,构建和谐社会,越来越成为河南各级政府高度关注的一个重要问题.测量与判断现有收入分配政策公平度,国际惯例是通过基尼系数[1-2].基尼系数是处于[0,1]区间的一个值,从数学角度讲,即使相差一个百分点,相对地看,其误差率也可能是高的.这种误差甚至可能影响经济学家和政府决策部门错误地判断收入分配差距状况,进而影响到收入分配政策和宏观经济政策的调整.因此,依据收集的数据,选择一种合适的、相对误差较小的算法就显得至关重要[3].目前,散见于各种文献的基尼系数估算数学模型很多,但最实用最基本的有哪些,在什么条件下选取什么模型,各种文献中都没有一个明确的说明;其次,洛伦兹曲线在基尼系数估算中起着非常重要的作用,但模拟洛伦兹曲线的计算机程序在各种文献中都不曾见到.本文首先通过分析比较各种算法的优缺点,建立了基尼系数估算4种不同条件下的数学模型,根据题设条件选择合适的数学模型,提高了基尼系数估算的准确率;然后,通过模拟洛伦兹曲线,且针对不同的数学模型设计计算机程序,实现基尼系数估算自动化;最后,作为例证,详细分析了河南省2003—2012连续10年城镇居民收入差距状况,进而为河南各级政府管理决策部门科学判断河南省城镇居民收入分配差距状况、调整收入分配政策和宏观经济政策提供数据和智力支持.
1 基尼系数估算的4种数学模型
关于基尼系数G的估算,大体上可分为两类[4]:直接计算法和拟合曲线法.在实际估算基尼系数时,主要采用直接计算法.所谓直接计算法就是依据收集的数据直接进行计算.直接计算法中最具代表性且操作性较好的有梯形法、矩形法、基尼计算法、抛物线法等4种不同的算法.4种数学模型适用条件、优点、缺点各不相同.基尼计算法依据数据可可以直接计算,其他3种方法估算基尼系数时均与洛伦兹曲线形态有关.从几何角度分析,其曲率的大小对计算方法的选择有很大影响,当洛伦兹曲线比较平缓时,梯形法或矩形法不失为一种好的计算方法;当洛伦兹曲线弯曲度较大时,由于梯形法或矩形法在求基尼系数的过程中都采用了以直代曲的方法,当然误差率就比较大,这时就应该选择抛物线方法[5].
下面给出常见的基尼系数估算数学模型以及各种模型适用条件、优点、缺点[6-7].
1.1 梯形法
模型1 把人口按收入从低到高分成n组,设第i(1≤i≤n)组人口占总人口的比例为Pi,其相应的收入占总收入的比例为Ii,则
梯形法的适用条件:洛伦兹曲线比较平缓或随着人口百分比的累加对应人口的收入百分比呈现平稳增加态势.优点:适用范围广,正常情况下的首选方法.缺点:当洛伦兹曲线弯曲度较大或随着人口百分比的累加对应人口的收入百分比呈现较快增加态势时,该方法得到的结果误差较大,这时应使用抛物线方法.
1.2 基尼计算法
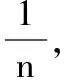
基尼计算法的适用条件:考察各收入阶层时,各阶层人口占总人口的比例需要相同.优点:可以通过已知数据直接计算,无须考虑洛伦兹曲线的形态.缺点:适用范围窄,考察各收入阶层时,人口必须等比例划分.
1.3 矩形法
模型3 把人口按收入从低到高分成n组,设第i(1≤i≤n)组人口占总人口的比例为Pi,其相应的收入占总收入的比例为Ii,则
矩形法的适用条件:同梯形法.矩形法与梯形法求基尼系数的思想是相似的,只不过在以直代曲的过程中分别用矩形与梯形代替了曲边梯形.
梯形法、矩形法、基尼计算法是估算基尼系数常见的3种方法.方法不同,其繁简程度、计算结果、误差率也不尽相同.一般情况下,它们之间没有必然的联系,但是在人口等分的条件下,梯形法、矩形法、基尼计算法[4]是等价的.
1.4 抛物线法
梯形法或矩形法是把洛伦兹曲线分成若干段,每段用直线代替曲线弧,即把I=I(P)逐段用线性函数代替.当洛伦兹曲线弯曲度较大时,梯形法、矩形法求基尼系数的误差会变大(会造成对基尼系数的明显低估).为了提高准确度,可以考虑在小范围上用二次函数I=ap2+bp+c来近似代替I=I(P),用对称轴平行于y轴的抛物线上的一段弧来近似替代原来的曲线弧(以曲代曲),此方法称为抛物线法[5].
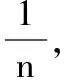
抛物线法的适用条件:洛伦兹曲线弯曲度较大或随着人口百分比的累加对应人口的收入百分比呈现较快增加态势.优点:适用于特殊情形下的基尼系数计算,如考察对象收入差距较大时.缺点:人口必须等比例划分且划分组数必须为偶数.
2 4种数学模型的计算机程序设计
2.1 数据处理
begin
Gp[0…99]//存放Gp的数组
Gi[0…99]//存放Gi的数组
输入数据对数⟹n
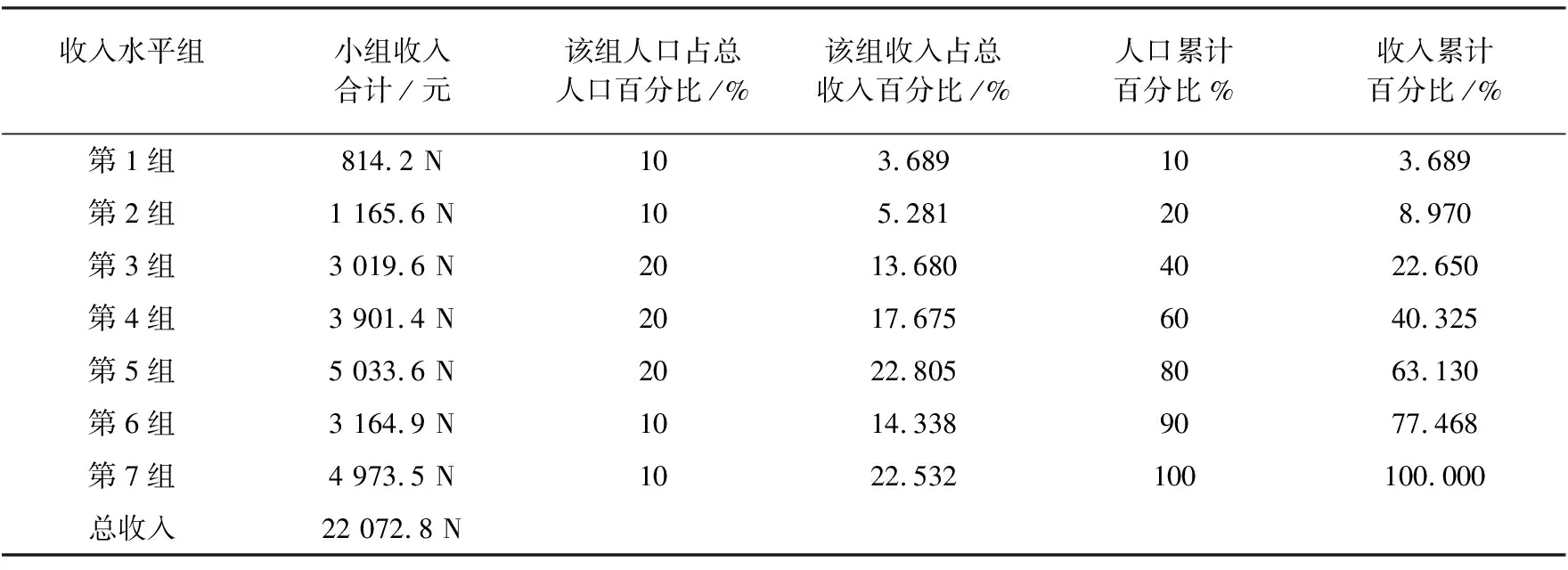
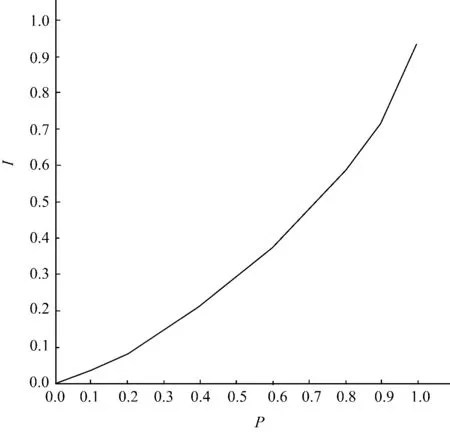
for (k=0;k 第k对数据的第一个数据⟹Gp[k] 第k对数据的第二个数据⟹Gi[k] } end 数据处理是为4种模型计算基尼系数作数据准备的. G1、G2、G3和G4分别存放梯形法、基尼计算法、矩形法和抛物线法计算的结果,分别对应模型1、模型2、模型3、模型4. begin 0⟹G⟹gi_sum⟹i while (i 0⟹g1⟹j while (j<=i) { g1+Gi[j]/100⟹g1 gi_sum+Gi[i]/100⟹gi_sum g=g+2*g1*Gp[i]/100-Gi[i]/100* Gp[i]/100 j=j+1 } i=i+1 } G1=1-g; Print G1//输出梯形法结果; end //梯形法结果; begin 0⟹g2⟹i for (;i g2=g2+i*Gi[i]/100 gi_sum=gi_sum+Gi[i]/100 } u=gi_sum/n for (i=0;i for (j=0;j if (Gi[i]-Gi[j]>0) G2=G2+Gi[i]/100-Gi[j]/100; else G2=G2+Gi[j]/100-Gi[i]/100; G2=G2/2/u/n/n; Print G2 //输出基尼计算法结果 end //基尼计算法结果; begin 0⟹G3⟹i for (;i 0⟹G31⟹j for (;j<=i;j++) G31=G31+Gp[j]/100 G3=G3+2*Gi[i]/100*G31-Gi[i]/100* Gp[i]/100 } Print G3-1//输出矩形法结果; end //矩形法结果; begin 0⟹G⟹G41⟹i for (;i G41=G41+Gi[i]/100; if(i!=n-1) G4=G4+(2+(i+1)%2*2)*G41; } print 1-2*(1+G4)/3/n //输出抛物线法结果. end //抛物线法结果 该部分具体给出梯形法、基尼法、矩形法和抛物线法计算基尼系数的程序. begin 520⟹x_width//x坐标轴的长度 480⟹y_height//y坐标轴的长度 Line((0,y_height,(x_width,y_height))//画横坐标轴线 Line((x_width,y_height),(x_width-5,y_height-5)) Line((x_width,y_height),(x_width-5,y_height+5)) for (i=0;i Print(0.i); //书写横坐标轴上的坐标 Line((i,y_height),(i,y_height-5));//画横坐标轴上的竖线 } print(“P”) //书写横坐标轴上的P Line((start_xy,start_xy),(start_xy,y_height)) //画纵坐标轴 Line((start_xy,start_xy),(start_xy-5,start_xy+5)) Line((start_xy,start_xy),(start_xy+5,start_xy+5)) System.Windows.Forms.Label[] y_label=newLabel [y_height/step_xy+2] for (i=y_height;i>step_xy;i=i-step_xy) { Print(0.j) //书写纵坐标轴上的坐标 Line((start_xy,i),(start_xy+5,i))//画纵坐标轴上的横线 } print(“I”) //书写纵坐标轴上的I if (mycheckbox.Checked==true)//如果选择连线 { oldx=start_xy,oldy=y_height for(i=1;i newx=((pi)+0.5)*step_xy/10 newy=((Ii)+0.5)*step_xy/10 Line(oldx,oldy),(newx+start_xy,y_height-newy))//画线 oldx=newx+start_xy oldy=y_height-newy } } 0⟹x⟹y for(i=0;i //根据数据准备计算第i个点的坐标 x=(pi+0.5)*step_xy/10+start_xy y=y_height-(Ii+0.5)*step_xy/10 Point(x-1,y,1,1)//画点 } end 该部分给出模拟洛伦兹曲线图形的程序.由于选取的数据是离散的,因此准确绘制洛伦兹曲线的图形是不可能的,这里模拟的洛伦兹曲线是根据一些离散点串联而成的. 依据河南省2003—2012年城镇居民人均可支配收入数据,计算并分析河南省2003—2012年连续10年城镇居民收入差距(基尼系数)状况. 由河南统计年鉴可查阅河南省2003—2012年城镇居民人均可支配收入数据,详见表1. 表1[9] 河南省2003—2012年城镇居民人均可支配收入数据一览表 注:表1数据来源于河南统计年鉴—按收入等级划分的河南省城镇居民家庭生活基本情况,单位:元. (1)首先分年度计算出城镇居民收入分配差距状况—基尼系数,这里以2012年为例详细说明,其他年份只列出计算结果. 根据表1,按收入等级从低到高排序,详细计算出2012年河南省城镇居民人口累计百分比和相应收入累计百分比,详见表2. 表2 河南省2012年城镇居民人口和收入累计百分比数据表 注:表2中第1组到第7组分别对应最低收入户组、低收入户组、…、最高收入户组等7个组别;第i组总收入=第i组人均收入×第i组人数=第i组人均收入×第i组人口占抽样总人口的比例×抽样总人口数,其中N为抽样总人口数. (2)依据表2,把Pi和Ii的值代入基尼系数估算程序,梯形法、矩形法求得的2012年基尼系数均为0.270(由于人口不是等比例分组,这里不能使用基尼法和抛物线法).同理可求得其他年份的基尼系数,详见表3,表3中河南省城镇居民收入基尼系数取梯形法和矩形法的平均值. 表3 河南省2003—2012年城镇居民收入基尼系数表(并于全国基尼系数比较) (3)洛伦兹曲线模拟 限于篇幅,这里仅给出2012年收入分配曲线—洛伦兹曲线模拟图(如图1). 输入Pi和Ii的值,由2.3节即生成洛伦兹曲线模拟图形. 图1 2012年河南省城镇居民收入分配曲线—洛伦兹曲线模拟图 (4)数据分析 从表3可见,反映河南省2003—2012年连续10年城镇居民收入差距状况的基尼系数在0.267到0.281之间,年度变化幅度最小值是0.001,最大值是0.014.按照国际惯例这说明收入分配状况是比较合理的, 但这与人们熟知的情况相距甚远,对照全国基尼系数也可发现这一情况.之所以出现这种现象,笔者认为主要有三个原因:一是数据收集失真.由于种种原因入户收集的数据不能真实反映居民收入情况,数据收集方法缺乏合理性、科学性,忽略了城镇居民在新型经济结构背景下收入多元化的特点,把工资性收入、经营性收入看做主要收入来源,财产性收入、转移性收入等被忽略或边缘化,收集的数据未能真实反映城镇居民收入全貌;二是收集数据的样本空间或对象没有兼顾到社会各个阶层、各种职业特别是一些高收入群体.要使收集数据的样本空间具有代表性,在选取样本时就必须兼顾到社会各个阶层、各种职业特别是一些低收入和高收入群体.由于我国缺乏健全的财产登记和纳税制度,某些人的巨额财产和巨额收入,无法全部显示出来,更不可能在住户调查中如实填报.一些特殊行业的高收入,某些职业的高福利,个别人享有的非法收入、灰色收入、隐形收入基本上是不报或漏报的;三是样本空间的建立缺乏合理性、科学性,未能真实反映河南省城镇居民收入状况.如各个收入阶层所占样本空间的实际比例与统计年鉴的数据严重不符,正常的情况应该符合正态分布中间大两头小,即最低收入组和最高收入组占比较小,而偏于中间的收入组占比较大.从表1可见,城镇居民按收入从低到高被分成7组,7个小组所占比例基本上是:10%,10%,20%,20%,20%,10%,10%,在一个比较完备的真实的样本空间各个收入组所占比例不应该如此分布.由于以上三个原因,导致了基尼系数明显低估,未能真实反映河南省城镇居民收入差距状况.2.2 4种数学模型计算方法的程序实现[8]
2.3 洛伦兹曲线模拟的程序实现[8]
3 例证分析