基于属性层次模型的岗位工资排序
庞进丽
(河南师范大学 数学与信息科学学院, 河南 新乡453007)
0 引言
岗位工资是指以岗位劳动责任、劳动强度、劳动条件等评价因素确定的岗位系数为依据,再通过一定的对应或转换关系计算出的工资数额[1].确定岗位工资的关键是根据不同的要素或评价标准对各岗位进行评估,得出各岗位的岗位系数(权重)或相对价值,这直接关系到岗位工资制度的成败.对此,文献[2]针对企业中的专业技术岗位评价,主要侧重于对有关原则的理论研究.文献[3-4]将主成分分析法运用到岗位评价过程中,这便于找到影响岗位评价的主要因素,但运算时需要尽可能使主成分的表达式中各因素的系数趋于两端(0或1).文献[5]研究了要素计点法在企业中的应用,但工作量大,用时长.文献[6]基于粗糙集差别矩阵的属性重要度,建立了岗位评价方法.文献[7]提出了基于层次分析法的岗位工资确定方法.为了促进岗位工资管理的科学性,本文就属性层次模型在岗位工资排序中的应用进行探讨.
属性层次模型(Attribute Hierarchical Model,AHM)是北京大学程乾生教授于1997年创立的.程乾生教授在球赛模型及属性测度的基础上,建立了相对属性测度和属性判断矩阵的概念,提出了一种新的无结构决策方法[8].
1 AHP和AHM的模型分析
1.1 AHP
层次分析法(Analytic Hierarchy Process, AHP)的特点是把复杂问题中的各种因素通过划分层次,根据主观判断(主要是两两比较),两两比较同一层次元素的相对重要性并量化,计算所有元素对目标的相对权重并进行排序.
设u1,u2,…,un为n个物体,它们的质量分别是g1,g2,…,gn.若已知它们两两之间的质量比,准则C为质量,在准则C下即按质量大小,对u1,u2,…,un进行排序.
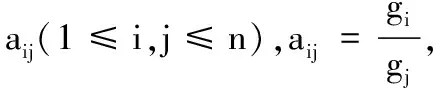
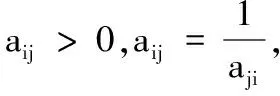
一致的(aij)n×n物理意义是:甲物比乙物重,乙物比丙物重,则甲物比丙物重.从决策意义上说,一致的(aij)n×n意义是:对物体质量的两两比较判断是正确的,进而做出的排序也是正确的.

1.2 AHM
在现实生活中,很多都是质量模型尚未描述的“意外”现象.在中外战争和体育比赛中,以弱胜强、出人意料的事情时有发生.像球类比赛、棋类比赛以及散打、击剑等运动项目,运动成绩只有通过两两比赛之后才能确定.甲队胜乙队,乙队胜丙队,但甲队却不一定能胜丙队.这就要建立不同于质量模型的比赛模型.
设u1,u2,…,un为n个球队,每两个球队进行1场比赛,每场比赛为1分.ui和uj比赛(i≠j),ui得分率为μij,uj得分率为μji,准则C为得分.若在准则C下,已知μij(1≤i,j≤n),对u1,u2,…,un按得分多少进行排序.
得分率应满足0≤μij≤1,0≤μji≤1,1≤i,j≤n,且两个球队的得分率应满足:
(1)μij+μji=1,i≠j;
(2)μii=0(自己跟自己比赛,没有意义),∀i=1,2,…,n.
μij就是相对属性测度,μij>μji表示ui比uj强,若ui>uj,uj>uk时,ui>uk,这是一致性.
在排序方面,ui的总得分为:
又由μij+μji=1,i≠j,μii=0,所以所有参赛球队的得分总和为:
定义1[8]设u1,u2,…,un为n个元素两两比较元素ui和uj(i≠j)对准则C的重要性.假设ui和uj对准则C的重要性分别记为μij和μji,若
(1)μij≥0,μji≥0,1≤i,j≤n;
(2)μij+μji=1;
(3)μii=0(ui和本身的比较没有意义),
则称μij为相对属性测度,称μij所组成的n阶方阵(μij)n×n为属性判断矩阵.
定义2[8]若μij>μji,则称ui比uj相对强(相对重要),记作ui>uj.若ui>uj,uj>uk(1≤i,j≤n)时,ui>uk,则称(μij)n×n具有一致性.
定理1[8]设

Ii={j|g(μij)=1,1≤j≤n},
则
(1)ui>uj的充分必要条件是g(μij)=1;
(2) 属性判断矩阵(μij)n×n具有一致性的充分必要条件是 ∀i=1,2,…,n,当Ii非空时,
定理1给出了属性判断矩阵一致性的检验方法.
定义3[9]令
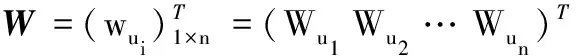
一种简单的一致性检验方法是:按wui的排序对(μij)n×n逐行检验.如果通过,则表明(μij)n×n具有一致性.上述定义、定理说明,AHM基于球赛模型.
2 AHM与AHP的区别和联系
因为层次分析法基于质量模型,而属性层次模型基于球赛模型,所以,在将人的主观判断量化的过程中,判断矩阵的构成、确定排序向量的算法、方法的简捷性等都不同[8-9].在AHP中,正互反判断矩阵(aij)n×n中的元素aij是通过两两比较,由元素相对重要性按1~9比例标度赋值给出的,矩阵表现为正互反判断矩阵.应用AHP时,需要用积法、和法或根法计算判断矩阵的特征根和特征向量,要计算一致性指标和随机一致性指标,来对判断矩阵进行一致性检验.一旦未通过一致性检验,就会前功尽弃,必须重新返工,从头再来.计算量大,过程烦琐,效率低.究其原因在于,人们在进行两两比较时,主要凭主观意识去判断,一开始就无法确保正互反判断矩阵的一致性,也就无法保证应用AHP的一次性成功.现在,大量文献研究了互反判断矩阵不一致时的“补救办法”,理论性上更严谨了,但简捷性和实用性却相应降低了.
在AHM中,属性判断矩阵(μij)n×n的元素μij可通过建立属性测度函数确定,以实现主观判断的量化.属性判断矩阵表现出类似于互补判断矩阵的一些特点,主要表现在:属性判断的主对角线上的元素全为0,而互补判断矩阵的主对角线上的元素却全为0.5.应用AHM时,不需要计算属性判断矩阵的特征根和特征向量,不需要计算一致性指标和随机一致性指标,很容易进行一致性检验,只需做一些加、乘、除运算即可.
但是,AHM和AHP都是解决无结构决策问题的方法,从总体上看,应用它们去解决问题的基本步骤大体相同,一般都分成三步,并且以第二步作为关键步骤,而AHM的优点主要表现在第二步上[9].
Step1 建立递阶层次结构;
Step2 构造判断矩阵,计算相对权重;
Step3 计算各个因素对系统目标的综合权重,进行决策.
应用AHM和AHP解决问题的步骤大体相同,且可从(aij)n×n得出(μij)n×n.但是,构造过程中,要注意保持两两元素之间的强弱关系不变.
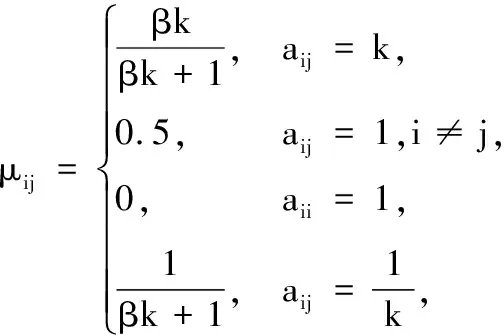
其中:k∈N+且k≥2,β≥1,则从(aij)n×n可以得到(μij)n×n.
通常取β=1或β=2.当β→∞时,得到极端的情况,可以较明确地确定属性测度和强弱关系:当aij=k>1时,μij=1;当aij=1(i≠j)时,μij=0.5;当aij<1时,μij=0.
如果采用其他的比例标度,正互反矩阵(aij)n×n中的元素aij可能是更一般的数.若令
也可从(aij)n×n得到(μij)n×n.
3 应用举例
下面结合文献[7]的研究,讨论属性层次模型在岗位工资排序中的应用.在文献[7]中,为了改善某公司薪酬分配状况,通过走访专家,以技术员、统计员、会计、劳资人员为例,对岗位责任和相对重要性进行判断,研究岗位工资问题.
Step1 建立递阶层次结构
按照AHP建立的确定岗位工资的层次结构图见文献[7].
Step2 构造属性判断矩阵,计算相对属性权重(层次单排序)
文献[7]提供的A—B层的正互反判断矩是

B1—C,B2—C,B3—C层的正互反判断矩阵依次是
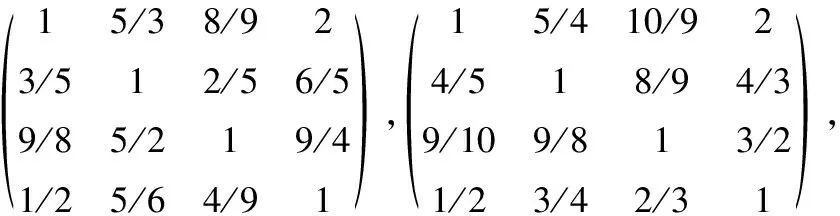
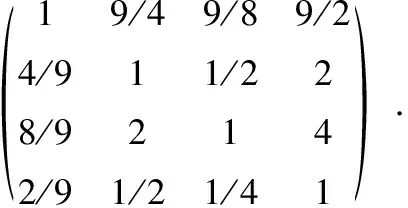
确定的各层次属性判断矩阵以及相对属性权重(层次单排序),结果见表1—表4.
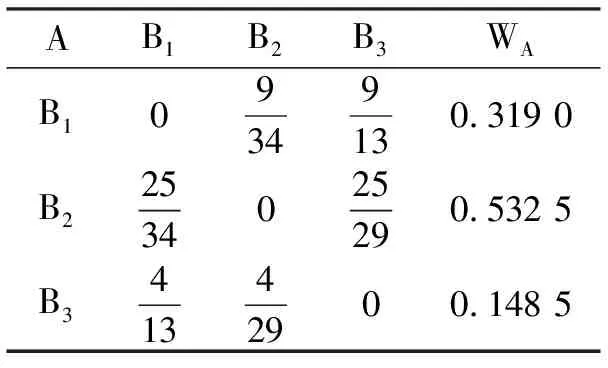
表1 A—Bj的属性判断矩阵及相对属性权重
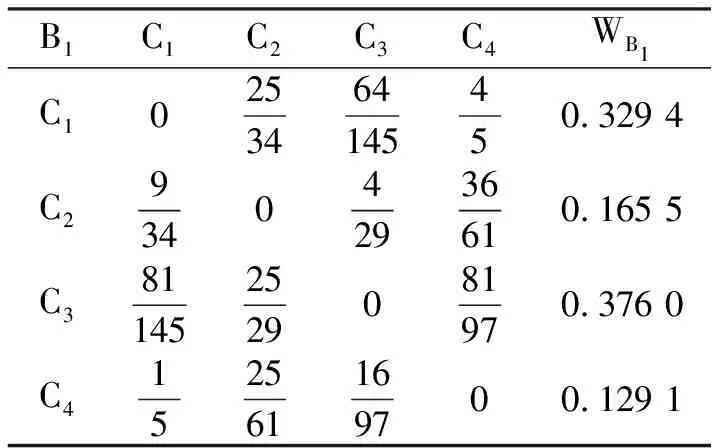
表2 B1—Cj的属性判断矩阵及相对属性权重

表3 B2—Cj的属性判断矩阵及相对属性权重
Step3 层次总排序
记Ci(i=1,2,3,4)相对于A的综合总权重为WCi,则
(0.3373 0.2123 0.3247 0.1258)T.
按照从重要到不重要的层次总排序是:C1(技术员)、C3(会计)、C2(统计员)、C4(劳资人员),总排序的结果同文献[7],但是,本文中的方法比文献[7]更加简易.
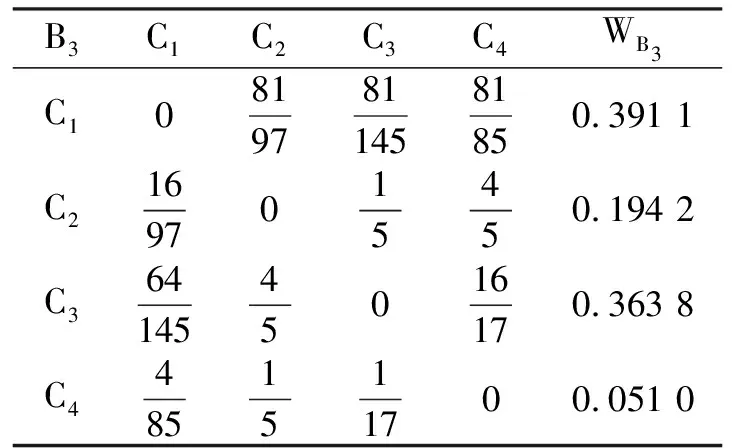
表4 B3—Cj的属性判断矩阵及相对属性权重
4 结语
基于属性层次模型(AHM)进行了岗位工资排序的实证分析.与层次分析法(AHP)相比,AHM的优点就在于简便地确定因素的相对权重.由于属性判断矩阵保持了正互反矩阵中两两元素间的重要或强弱关系,表现出与互补判断矩阵相似的特点,因此AHM更符合人在判断时的客观实际,具有较强的科学性.实例表明,所建模型合理、简单、实用.从岗位工资排序的实证分析看,属性层次模型(AHM)具有较强的说服力,为管理者发现问题、解决问题提供了科学依据,这对提高我国的企事业管理水平具有一定意义[10-13].目前,针对岗位工资排序的软科学方法的研究还需要进一步深入,属性判断矩阵的建立,其科学性还需要进一步探讨.

